霍夫变换(Hough Transform)
文章目录
- 1. 什么是霍夫变换
- 2. 霍夫直线检测
- 2.1 霍夫直线检测的具体步骤
- 2.2 霍夫直线检测的优缺点
- 2.3 OpenCV中霍夫直线检测的应用
- 2.3.1 标准霍夫检测
- 2.3.2 概率霍夫检测
- 3. 霍夫圆检测
- 4. 源码仓库地址
1. 什么是霍夫变换
霍夫变换(Hough Transform)是图像处理中的一种特征提取技术,该过程在一个参数空间中通过计算累计结果的局部最大值得到一个符合该特定形状的集合作为霍夫变换结果。
霍夫变换于1962年由PaulHough首次提出,最初的Hough变换是设计用来检测直线和曲线,起初的方法要求知道物体边界线的解析方程,但不需要有关区域位置的先验知识。这种方法的一个突出优点是分割结果的Robustness,即对数据的不完全或噪声不是非常敏感。然而,要获得描述边界的解析表达常常是不可能的。后于1972年由Richard Duda & Peter Hart推广使用,经典霍夫变换用来检测图像中的直线,后来霍夫变换扩展到任意形状物体的识别,多为圆和椭圆。霍夫变换运用两个坐标空间之间的变换将在一个空间中具有相同形状的曲线或直线映射到另一个坐标空间的一个点上形成峰值,从而把检测任意形状的问题转化为统计峰值问题。
霍夫变换在OpenCV中分为霍夫线变换和霍夫圆变换两种。
2. 霍夫直线检测
Hough直线检测的基本原理在于利用点与线的对偶性,在我们的直线检测任务中,即图像空间中的直线与参数空间中的点是一一对应的,参数空间中的直线与图像空间中的点也是一一对应的。这意味着我们可以得出两个非常有用的结论:
1)图像空间中的每条直线在参数空间中都对应着单独一个点来表示;
2)图像空间中的直线上任何一部分线段在参数空间对应的是同一个点。
因此Hough直线检测算法就是把在图像空间中的直线检测问题转换到参数空间中对点的检测问题,通过在参数空间里寻找峰值来完成直线检测任务。
2.1 霍夫直线检测的具体步骤
- 彩色图像->灰度图;
- 去噪(高斯核);
- 边缘提取(梯度算子、拉普拉斯算子、canny、sobel);
- 二值化(判断此处是否为边缘点,就看灰度值==255);
- 映射到霍夫空间(准备两个容器,一个用来展示hough-space概况,一个数组hough-space用来储存voting的值,因为投票过程往往有某个极大值超过阈值,多达几千,不能直接用灰度图来记录投票信息);
- 取局部极大值,设定阈值,过滤干扰直线;
- 绘制直线、标定角点。
2.2 霍夫直线检测的优缺点
优点:Hough直线检测的优点是抗干扰能力强,对图像中直线的残缺部分、噪声以及其它共存的非直线结构不敏感,能容忍特征边界描述中的间隙,并且相对不受图像噪声的影响。
缺点:Hough变换算法的特点导致其时间复杂度和空间复杂度都很高,并且在检测过程中只能确定直线方向,丢失了线段的长度信息。由于霍夫检测过程中进行了离散化,因此检测精度受参数离散间隔制约。
2.3 OpenCV中霍夫直线检测的应用
OpenCV的中用函数HoughLines(标准)和HoughLinesP(基于统计)来检测图像中的直线,函数原型如下:
2.3.1 标准霍夫检测
lines = cv.HoughLines( image, rho, theta, threshold[, lines[, srn[, stn[, min_theta[, max_theta]]]]] )
参数说明:
lines:返回值(ρ,θ),ρ以像素为单位,θ以弧度为单位;
rho:累加器的距离分辨率(以像素为单位);
theta:累加器的角度分辨率(弧度);
threshold:阈值,仅大于的才可以被返回;
srn:对于多尺度Hough变换,它是距离分辨率rho的除数。粗累加器距离分辨率为rho,精确累加器分辨率为rho/srn。如果srn=0和stn=0,则使用经典Hough变换。否则,这两个参数都应为正值;
stn:对于多尺度Hough变换,它是距离分辨率θ的除数;
min_theta:对于标准和多尺度Hough变换,检查直线的最小角度。必须介于0和最大θ之间;
max_theta:对于标准和多尺度Hough变换,检查直线的最大角度。必须介于min_theta和CV_PI之间。
2.3.2 概率霍夫检测
lines = cv.HoughLinesP( image, rho, theta, threshold[, lines[, minLineLength[, maxLineGap]]] )
参数说明:
lines:返回两个端点的坐标;
rho:累加器的距离分辨率(以像素为单位);
theta:累加器的角度分辨率(弧度);
threshold:阈值,仅大于的才可以被返回;
minLineLength:最小行长度,小于该长度的线段将被拒绝;
maxLineGap:同一直线上连接点的最大允许间距。
测试代码如下:
import cv2 as cv
import numpy as np
import matplotlib.pyplot as pltsrc = cv.imread("demo-line.jpg")
img = src.copy()# 二值化图像(Canny边缘检测)
gray_img = cv.cvtColor(img, cv.COLOR_BGR2GRAY)
dst_img = cv.Canny(gray_img, 50, 150)# 霍夫线变换
lines = cv.HoughLines(dst_img, 0.5, np.pi / 180, 300)# 将检测的线绘制在原图上(注意是极坐标)
for line in lines:rho, theta = line[0]a = np.cos(theta)b = np.sin(theta)# 找两个点x0 = rho * ay0 = rho * bx1 = int(x0 + 1000 * (-b))y1 = int(y0 + 1000 * a)x2 = int(x0 - 1000 * (-b))y2 = int(y0 - 1000 * a)cv.line(img, (x1, y1), (x2, y2), (255, 0, 0), 3)# 显示图像
plt.subplot(311), plt.imshow(src, 'gray'), plt.title('src_img'), plt.axis('off')
plt.subplot(312), plt.imshow(dst_img, 'gray'), plt.title('canny_img'), plt.axis('off')
plt.subplot(313), plt.imshow(img, 'gray'), plt.title('HoughLines_img'), plt.axis('off')
plt.show()
效果如下:

3. 霍夫圆检测
霍夫圆变换的基本思路是认为图像上每一个非零像素点都有可能是一个潜在的圆上的一点,跟霍夫线变换一样,也是通过投票,生成累积坐标平面,设置一个累积权重来定位圆。
OpenCV中使用cv2.HoughCircles函数来实现霍夫圆检测,其函数原型如下:
cv2.HoughCircles(image, method, dp, minDist[, circles[, param1[, param2[, minRadius[, maxRadius]]]]]) → circles
参数说明:
image:8位单通道图像,如果使用彩色图像,需要先转换成灰度图像;
method:定义检测图像中圆的方法,目前唯一实现的方法是cv2.HOUGH_GRADIENT;
dp:图像像素分辨率与参数空间分辨率的比值(官方文档上写的是图像分辨率与累加器分辨率的比值,它把参数空间认为是一个累加器,毕竟里面存储的都是经过的像素点的数量),dp=1,则参数空间与图像像素空间(分辨率)一样大,dp=2,参数空间的分辨率只有像素空间的一半大;
minDist:检测到的圆的中心,(x,y)坐标之间的最小距离。如果minDist太小,则可能导致检测到多个相邻的圆。如果minDist太大,则可能导致很多圆检测不到;
param1:用于处理边缘检测的梯度值方法;
param2:cv2.HOUGH_GRADIENT方法的累加器阈值。阈值越小,检测到的圆越多;
minRadius:半径的最小大小(以像素为单位);
maxRadius:半径的最大大小(以像素为单位)。
测试代码如下:
import cv2
import numpy as np
import matplotlib.pyplot as pltimg = cv2.imread('demo-circle.jpg',0)
img = cv2.medianBlur(img,5)
cimg = cv2.cvtColor(img,cv2.COLOR_GRAY2BGR)
circles = cv2.HoughCircles(img,cv2.HOUGH_GRADIENT,1,200,param1=50,param2=30,minRadius=0,maxRadius=0)
circles = np.uint16(np.around(circles))
for i in circles[0,:]:# draw the outer circlecv2.circle(cimg,(i[0],i[1]),i[2],(0,255,0),2)# draw the center of the circlecv2.circle(cimg,(i[0],i[1]),2,(0,0,255),3)plt.subplot(121), plt.imshow(img, 'gray'), plt.title('src_img'), plt.axis('off')
plt.subplot(122), plt.imshow(cimg, 'gray'), plt.title('HoughCircles_img'), plt.axis('off')
plt.show()
效果如下:

4. 源码仓库地址
🌼 图像处理、机器学习的常用算法汇总
相关文章:

霍夫变换(Hough Transform)
文章目录 1. 什么是霍夫变换2. 霍夫直线检测2.1 霍夫直线检测的具体步骤2.2 霍夫直线检测的优缺点2.3 OpenCV中霍夫直线检测的应用2.3.1 标准霍夫检测2.3.2 概率霍夫检测 3. 霍夫圆检测4. 源码仓库地址 1. 什么是霍夫变换 霍夫变换(Hough Transform)是图像处理中的一种特征提取…...

【每日挠头算法题(2)】压缩字符串|仅执行一次字符串交换能否使两个字符串相等
文章目录 一、压缩字符串思路 二、仅执行一次字符串交换能否使两个字符串相等思路1:计数法思路2:模拟法 总结 一、压缩字符串 点我直达~ 思路 使用双指针法 大致过程如下: 使用双指针,分别读(read)&…...

V4L2框架解析
和你一起终身学习,这里是程序员Android 经典好文推荐,通过阅读本文,您将收获以下知识点: 一、概览二、流程简介三、关键结构体四、模块初始化五、处理用户空间请求 一、概览 相机驱动层位于HAL Moudle与硬件层之间,借助linux内核驱…...
Trie树模板与应用
文章和代码已经归档至【Github仓库:https://github.com/timerring/algorithms-notes 】或者公众号【AIShareLab】回复 算法笔记 也可获取。 文章目录 Trie树(字典树)基本思想例题 Trie字符串统计code关于idx的理解 模板总结应用 最大异或对分…...
)
【华为OD统一考试B卷 | 200分】跳格子游戏(C++ Java JavaScript Python)
文章目录 题目描述输入描述输出描述用例C++javajavaScriptpython题目描述 地上共有N个格子,你需要跳完地上所有的格子,但是格子间是有强依赖关系的,跳完前一个格子后,后续的格子才会被开启,格子间的依赖关系由多组steps数组给出,steps[0]表示前一个格子,steps[1]表示st…...

该选哪个语言进修呢?
前言: 如今,计算机编程已经成为了许多工作领域中的必备技能。但是,现在的计算机语言有很多,这可能会让我们感到困惑:我应该从哪个语言开始呢?在这篇博客中,我们将详细分析当前流行的一些计算机…...

数据库实验三 数据查询一
任务描述 本关任务:按条件查询数据表的所有字段 为了完成本关任务,你需要掌握: 如何查询数据表的所有字段 相关知识 查询数据表 命令格式: select * from 数据表 where 查询条件 任务要求 打开province数据库 第一题 查询街…...

【Python百日进阶-Web开发-Peewee】Day244 - 数据库 Postgresql、CockroachDB
文章目录 六、数据库6.1 初始化数据库6.2 使用 Postgresql6.2.1 隔离级别 6.3 使用 CockroachDB 六、数据库 http://docs.peewee-orm.com/en/latest/peewee/database.html PeeweeDatabase对象表示与数据库的连接。该类Database使用打开数据库连接所需的所有信息进行实例化&…...

Vue 中的列表渲染
Vue 中的列表渲染 在 Vue 中,列表渲染是非常常见的操作。它允许我们将一个数组中的数据渲染为一个列表,从而实现数据的展示和交互。在本文中,我们将探讨 Vue 中的列表渲染的基本原理和用法,并给出一些实例代码来帮助读者更好地理…...

java 中的关键字
1. 面向对象编程(OOP) - 把程序中的实体看做对象,而不是过程或函数。OOP有3个基本特征:封装,继承和多态。 2. 类(Class) - 一个用于描述对象属性和方法的蓝图。 3. 对象(Object) - 类的实例化,也就是一个具体的实体。 4. 方法(Met…...

python序列化和结构化数据详解
序列化和结构化数据是计算机程序中非常重要的概念,它们的原理和应用在许多应用程序中都是必不可少的。Python作为一种高级编程语言,在序列化和结构化数据方面提供了很多优秀的解决方案。在本文中,我们将详细介绍Python中序列化和结构化数据的…...
PoseiSwap的趋势性如何体现?
DEX 代表了一种先进的意识形态,相对于 CEX 其更强调无许可、去中心化以及公开透明。然而随着 DeFi 赛道逐渐从 2021 年年底的高峰逐渐转向低谷,DEX 整体的交易量、TVL等数据指标也开始呈现下滑的趋势,DEX 正在面临发展的新瓶颈期。 在这样的背…...
西南交通大学智能监测 培训课程练习4
2023.056.07和09培训 项目实战 目录 一、infracore(基础核心层) 1.1database 1.2config 1.3util 二、业务领域模块 2.1structure模块 2.1.1domain层 2.1.2application层 2.1.3adapter层 2.2sensor模块 2.2.1domian层 2.2.2application层 2.2.…...
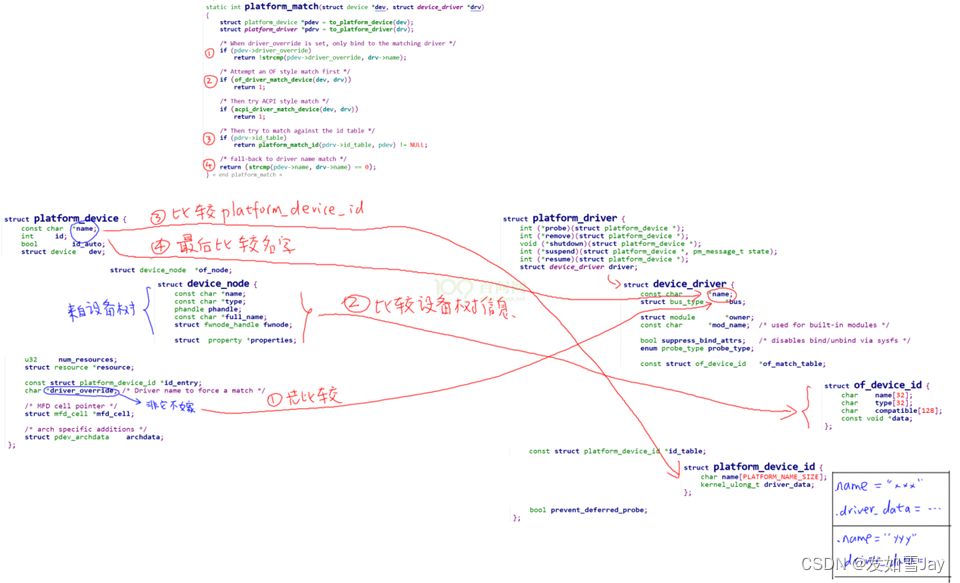
设备树的引入及简明教程
首先说明,设备树不可能用来写驱动。 设备树只是用来给内核里的驱动程序,指定硬件的信息。比如LED驱动,在内核的驱动程序里去操作寄存器,但是操作哪一个引脚?这由设备树指定。 需要编写设备树文件(dts: device tree s…...

MM32F3273G8P火龙果开发板MindSDK开发教程12 -获取msa311加速器的敲击事件
MM32F3273G8P火龙果开发板MindSDK开发教程12 -获取msa311加速器的敲击事件 1、功能描述 msa311可以识别单击、双击事件,类似手机上的点击返回,双击截屏功能。 单击,双击都能产生中断事件。 中断事件产生后,从对应的状态寄存器读…...

Maven聚合
在实际的开发过程中,我们所接触的项目一般都由多个模块组成。在构建项目时,如果每次都按模块一个一个地进行构建会十分得麻烦,Maven 的聚合功能很好的解决了这个问题。 聚合 使用 Maven 聚合功能对项目进行构建时,需要在该项目中…...
[架构之路-211]- 需求- 软架构前的需求理解:ADMEMS标准化、有序化、结构化、层次化需求矩阵 =》需求框架
目录 前言: 一、什么是ADMES: 首先,需求是分层次的: 其次,需求是有结构的,有维度的 再次,不同层次需求、不同维度需求之间可以相互转化(难点、经验积累) 最终,标准…...
基于前推回代法的连续潮流计算研究【IEEE33节点】(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

【双向链表】
双向链表 带头双向循环链表的实现1. 函数的声明2. 函数的实现3. 主函数测试 带头双向循环链表的实现 今天我们来实现一下带头双向循环链表,顾名思义,带头就是有哨兵位,哨兵位不是链表的头,它是连接头节点的一个节点,方…...

POSTGRESQL NEON - Serverless 式的POSTGRESQL 数据库的独特技能 分支数据
开头还是介绍一下群,如果感兴趣polardb ,mongodb ,mysql ,postgresql ,redis 等有问题,有需求都可以加群群内有各大数据库行业大咖,CTO,可以解决你的问题。加群请联系 liuaustin3 ,在新加的朋友会分到2群(共…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...
