二维计算几何全家桶
参考文章:范神的神仙博客
前置芝士
-
一些高中数学
-
向量的叉积:向量的点积为 a⋅b=∣a∣∣b∣cos<a,b>a\cdot b=|a||b|\cos<a,b>a⋅b=∣a∣∣b∣cos<a,b>,向量的叉积为 a×b=∣a∣∣b∣sin<a,b>a\times b=|a||b|\sin<a,b>a×b=∣a∣∣b∣sin<a,b>,在平面直角坐标系中 a(x1,y1),b(x2,y2)a(x_1,y_1),b(x_2,y_2)a(x1,y1),b(x2,y2),则 a×b=x1y2−x2y1a\times b=x_1y_2-x_2y_1a×b=x1y2−x2y1。容易发现叉积不满足交换律,不要写反。
存储及基本运算
我也不知道为什么到了这就突然不压行了。
struct qwq{//点 double x,y;
};
struct qaq{//线 qwq d,a,b;//d为a->b方向的单位向量
};
struct cir{//圆 qwq p;double r;//圆心及半径
};
inline qwq operator + (const qwq &a,const qwq &b){return {a.x+b.x,a.y+b.y};
}
inline qwq operator - (const qwq &a,const qwq &b){return {a.x-b.x,a.y-b.y};
}
inline qwq operator * (const qwq &a,const double &b){return {a.x*b,a.y*b};
}
inline qwq operator / (const qwq &a,const double &b){return {a.x/b,a.y/b};
}
inline double operator * (const qwq &a,const qwq &b){//点积 return a.x*b.x+a.y*b.y;
}
inline double operator ^ (const qwq &a,const qwq &b){//叉积 return a.x*b.y-b.x*a.y;
}
inline double len(qwq a){return sqrt(a.x*a.x+a.y*a.y);
}
inline qaq get(qwq a,qwq b){//已知两点构造直线qwq d=(b-a)/len(b-a);return {d,a,b};
}
点线基本问题
点到直线垂足
求完垂足显然就可以用初中知识求出点到直线距离,点关于直线对称点等,不一一展开。
inline qwq cz(qaq l,qwq p){return l.a+l.d*((p-l.a)*l.d);
}
点与直线位置关系
用叉积与 000 的大小关系可以判断顺时针/逆时针/在线上。
如果直线是向量,那可以进一步用点积判断点在向量上/延长线上/反向延长线上。
if(fabs(l.d^(p-l.a))<eps){if(((p-l.a)*(p-l.b))<eps) puts("ON_SEGMENT");//注意点与端点重合的情况,实质上是<=0else if((l.d*(p-l.a))<-eps) puts("ONLINE_BACK");else puts("ONLINE_FRONT");}else{if((l.d^(p-l.a))>eps) puts("COUNTER_CLOCKWISE");else puts("CLOCKWISE");}
直线与直线位置关系
共线用叉积判断,垂直用点积判断。
if(fabs(l1.d^l2.d)<eps) puts("2");//共线/平行else if(fabs(l1.d*l2.d)<eps) puts("1");//垂直else puts("0");//其它
判断两线段是否相交
- 快速排斥实验:定义一条线段占的区域为各边平行坐标轴且以该线段为对角线的矩形。当两个矩形不相交是两线段一定不相交。
- 跨立实验:若线段 aaa 两端点在线段 bbb 所在直线两侧且线段 bbb 两端点在线段 aaa 所在直线两侧,则通过了跨立实验。
发现通过了这两个实验之一都无法保证两线段相交,而将它们结合起来用就是充要条件了。
不要忘了跨立实验有端点在线段上的情况。(似乎写的有点丑)
inline bool check(qwq p1,qwq p2,qwq p3,qwq p4){//快速排斥实验 if(max(p1.x,p2.x)<min(p3.x,p4.x)) return 0;if(max(p3.x,p4.x)<min(p1.x,p2.x)) return 0;if(max(p1.y,p2.y)<min(p3.y,p4.y)) return 0;if(max(p3.y,p4.y)<min(p1.y,p2.y)) return 0;return 1;
}
inline int side(qwq p,qaq l){//跨立实验 double tmp=l.d^(p-l.a);if(fabs(tmp)<eps) return 0;if(tmp<-eps) return 1;return 2;
}
inline void solve(){l1=get(p1,p2),l2=get(p3,p4);if(!check(p1,p2,p3,p4)) puts("0");else{int a1=side(p1,l2),a2=side(p2,l2),a3=side(p3,l1),a4=side(p4,l1);if((a1!=a2||!a1||!a2)&&(a3!=a4||!a3||!a4)) puts("1");else puts("0"); }
}
求两直线交点
设交点为 ppp,则代入第一个直线的方程式得 p=a1+k⋅d1p=a_1+k\cdot d_1p=a1+k⋅d1,且同时 ppp 要满足在第二条直线上,即 (p−a2)×d2=0(p-a_2)\times d_2=0(p−a2)×d2=0,联立一下:(a1−a2+k×d1)×d2=0(a_1-a_2+k\times d_1)\times d_2=0(a1−a2+k×d1)×d2=0,叉积拆开即为 k=(a2−a1)×d2d1×d2k=\dfrac{(a_2-a_1)\times d_2}{d_1\times d2}k=d1×d2(a2−a1)×d2。
inline qwq jd(qaq l1,qaq l2){double k=((l2.a-l1.a)^l2.d)/(l1.d^l2.d);return l1.a+(l1.d*k);
}
求两线段距离
特殊情况是相交,答案为 000;其余情况就是端点到另一线段距离了,我是用垂足在不在线段上来判的,似乎又写丑了。
l1=get(p1,p2),l2=get(p3,p4);if(xj()){puts("0.0000000000");continue;}qwq p=cz(p1,l2);double ans=min(dis(p1,p3),min(dis(p1,p4),min(dis(p2,p3),dis(p2,p4)))); if(on(p,l2)) ans=min(ans,dis(p,p1));p=cz(p2,l2);if(on(p,l2)) ans=min(ans,dis(p,p2));p=cz(p3,l1);if(on(p,l1)) ans=min(ans,dis(p,p3));p=cz(p4,l1);if(on(p,l1)) ans=min(ans,dis(p,p4));printf("%.10lf\n",ans);
公共投影问题
给定 nnn 条线段,求是否存在一条直线使得这些线段在这条直线上的投影有公共点。
问题转化:假设存在,那么过公共点作直线垂线一定与每条线段都相交。而这条垂线一定可以通过平移使得它经过所有端点中的两个。于是枚举两个端点判断即可。
直线的旋转
向量 (x,y)(x,y)(x,y) 逆时针旋转 θ\thetaθ 度得到的向量为 (xcosθ−ysinθ,ycosθ+xsinθ)(x\cos\theta-y\sin\theta,y\cos\theta+x\sin\theta)(xcosθ−ysinθ,ycosθ+xsinθ),详见数学必修三。
inline qwq rotate(qwq a,double t){double si=sin(t),co=cos(t);return {a.x*co-a.y*si,a.y*co+a.x*si};
}
多边形问题
下面默认所有顶点都按逆时针顺序存储。
求多边形面积
任选一个点,把多边形拆成若干三角形即可根据叉积的几何意义计算:S=12∣∑i=1npi×pi%n+1∣S=\dfrac{1}{2}|\sum\limits_{i=1}^np_i\times p_{i\%n+1}|S=21∣i=1∑npi×pi%n+1∣,显然任意点直接取原点是最方便的。
判断凹/凸多边形
忽略相邻三点共线情况,凸多边形即相邻两边所成向量之间的叉积正负性始终相同。
p[0]=p[n],p[n+1]=p[1];int pre=0;rep(i,1,n){double tmp=(p[i+1]-p[i])^(p[i]-p[i-1]);if(fabs(tmp)<eps) continue;int now=(tmp>eps)?1:-1;if(!pre) pre=now;else if(pre!=now) return puts("0"),0;}
判断一个点是否在多边形内
这里是回转数算法。
把待判断的点 aaa 与多边形每一个顶点依次相连,相邻顶点之间会形成若干有方向的夹角。画图得知当且仅当这些夹角和为 000 时点在多边形外部。
注意 epsepseps 不要过小,容易炸。
inline bool on(qwq p,qaq l){if(p==l.a||p==l.b) return 1;double tmp=(p-l.a)^l.d;if(fabs(tmp)>eps) return 0;return p.x>=min(l.a.x,l.b.x)&&p.x<=max(l.a.x,l.b.x)&&p.y>=min(l.a.y,l.b.y)&&p.y<=max(l.a.y,l.b.y);
}
inline double jiao(qwq a,qwq b){double ans=acos(min(1.0,(a^b)/(len(a)*len(b))));//取min是为了避免一些精度误差带来的玄学问题 return ans;
}
inline bool pd(qaq l,qwq p){//判断正角还是负角return (l.d^(p-l.a))>eps;
}
inline void solve(){double now=0;rep(i,1,n){if(on(a,get(p[i],p[i+1]))) return puts("1"),void();//在多边形上 if(pd(get(a,p[i]),p[i+1])) now+=jiao(a-p[i],a-p[i+1]);else now-=jiao(a-p[i],a-p[i+1]);}if(fabs(now)<eps) puts("0");//在多边形外 else puts("2");
}
二维凸包
定义:包含给定的所有点的周长最小的凸多边形。
求凸包可以用 Andrew 算法在 O(nlogn)O(n\log n)O(nlogn) 的时间内求解。
先把所有点以 xxx 为第一关键字,yyy 为第二关键字升序排序。那么排完序的第一个点和最后一个点一定在凸包上,且以它们为分界线可以将凸包分为上下两部分,而两部分转弯的顺逆时针情况都是相同的。所以可以用单调栈维护,先求出下凸壳,再在没使用过的点中求出上凸壳。
实现的时候注意因为第一个点要用来更新上凸壳,所以开始不能记 vis[1]=1vis[1]=1vis[1]=1;最后栈内一定重复加了一个 111,所以要 top−−top--top−−。
inline void solve(){sort(a+1,a+n+1);s[++top]=1;rep(i,2,n){while(top>1&&((a[s[top]]-a[s[top-1]])^(a[i]-a[s[top]]))<0) vis[s[top]]=0,--top;vis[i]=1,s[++top]=i;}int pos=top;for(int i=n;i;--i) if(!vis[i]){while(top>pos&&((a[s[top]]-a[s[top-1]])^(a[i]-a[s[top]]))<0)vis[s[top]]=0,--top;vis[i]=1,s[++top]=i;}--top;
}
旋转卡壳
常用于求平面上最远点对。
首先显然最远点对的两个点一定都在凸包上,而逆时针遍历凸包的每一条边的过程中,离当前边所在直线距离最远的点也一定沿着逆时针方向旋转,于是维护这个最远点的位置,用这个点到当前边两端点的距离更新答案即可。
inline double dis(qwq a,qwq b){double x=a.x-b.x,y=a.y-b.y;return x*x+y*y;
}
inline double disl(qwq p,qaq l){return fabs(l.d^(p-l.a));
}
inline double kk(){p[tot+1]=p[1],p[0]=p[tot],nxt[tot]=1;rep(i,1,tot-1) nxt[i]=i+1;int now=2;double ans=0;rep(i,1,tot){qaq l=get(p[i],p[i+1]);while(disl(p[nxt[now]],l)>disl(p[now],l)) now=nxt[now];ans=max(ans,max(dis(p[i],p[now]),dis(p[i+1],p[now])));}return sqrt(ans);
}
半平面交
顾名思义,求解多个凸多边形的面积交问题。
先将所有边进行极角排序,即用 atan2(y,x)atan2(y,x)atan2(y,x) 求出 tanα=yx,α∈(−π,π]\tan\alpha=\dfrac{y}{x},\alpha\in(-\pi,\pi]tanα=xy,α∈(−π,π] 的角 α\alphaα ,不同的角按角的大小排序,相同的将位置更靠里的放在前面。
然后用一个 dequedequedeque 维护对答案可能有贡献的边及相邻边的交点。具体地,每加入一条边,先不断从队尾弹出已经不合法的交点,再不断从队首弹出已经不合法的交点,最后插入当前边已经当前边和之前的队尾的交点。
插入进行到最后时,可能队尾的一些点被队首卡掉了,而队首的点一直被后来加入的队尾们约束着,不可能被卡掉,所以要不断弹出队尾直至合法。
最后别忘了加入一下队尾和队首的交点。
构成一个多边形至少要三条边,若最终队列长度小于 333,说明面积交为 000。
inline bool in(qwq p,qaq l){return (l.d^(p-l.a))>eps;}
inline bool out(qwq p,qaq l){return (l.d^(p-l.a))<-eps;}
inline bool cmp(qaq l1,qaq l2){double p1=atan2(l1.d.y,l1.d.x),p2=atan2(l2.d.y,l2.d.x);if(fabs(p1-p2)>eps) return p1<p2;return in(l1.a,l2);
}
inline qwq jiao(qaq l1,qaq l2){double k=((l2.a-l1.a)^l2.d)/(l1.d^l2.d);return l1.a+l1.d*k;
}
inline void half(){sort(a+1,a+tot+1,cmp);rep(i,1,tot){if(l<=r&&fabs(q[r].d^a[i].d)<eps) continue;//判掉无用的平行边while(l<r&&out(jd[r],a[i])) --r;//当队列长为2且唯一交点不合法时先弹出队首会出错,必须先弹队尾while(l<r&&out(jd[l+1],a[i])) ++l;//交点是从队首的下一个开始产生的q[++r]=a[i];if(l<r) jd[r]=jiao(a[i],q[r-1]);}while(l<r&&out(jd[r],q[l])) --r;if(l<r) jd[r+1]=jiao(q[l],q[r]),++r;n=r-l;rep(i,1,n) p[i]=jd[i+l];p[n+1]=p[1];
}
圆相关问题
三角形内切圆
求出两条角平分线,交点即为圆心。半径即为点到直线距离。
inline qaq pf(qaq l1,qaq l2){//求角平分线qwq d=(l1.d+l2.d)/len(l1.d+l2.d);return {d,l1.a,l1.a+d};
}
inline cir nqy(qwq p1,qwq p2,qwq p3){cir ans;qaq l1=pf(get(p1,p2),get(p1,p3));qaq l2=pf(get(p2,p1),get(p2,p3));ans.p=jd(l1,l2),ans.r=dis(ans.p,get(p1,p2));return ans;
}
三角形外接圆
求两条中垂线交点即可。
inline qaq zcx(qaq l){//中垂线qwq mid={(l.a.x+l.b.x)/2,(l.a.y+l.b.y)/2};return {{l.d.y,-l.d.x},mid};
}
inline cir wjy(qwq p1,qwq p2,qwq p3){qaq l1=zcx(get(p1,p2)),l2=zcx(get(p2,p3));qwq p=jd(l1,l2);return {p,dis(p,p1)};
}
圆和直线交点
在保证有交点的前提下,求出圆心到直线垂足后勾股定理即可。
inline void query(qaq l){vector<qwq> ans;qwq cz=l.d*(l.d*(c.p-l.a))+l.a;double d1=len(cz-c.p),d2=sqrt(c.r*c.r-d1*d1);ans.push_back(cz+l.d*d2),ans.push_back(cz-l.d*d2);sort(ans.begin(),ans.end());for(qwq tmp:ans) printf("%.8lf %.8lf ",tmp.x,tmp.y);putchar('\n');
}
圆与圆交点
发现以两圆心和其中一个交点为顶点的三角形三边均已知,就可以用余弦定理求出其中一个角,旋转经过两圆心的直线即可。
inline void query(cir c1,cir c2){vector<qwq> ans;double dis=len(c1.p-c2.p);qaq l=get(c1.p,c2.p);double t=acos((c1.r*c1.r-c2.r*c2.r+dis*dis)/(2*c1.r*dis));qwq d1=rotate(l.d,t),d2=rotate(l.d,2*pi-t);ans.push_back(c1.p+d1*c1.r),ans.push_back(c1.p+d2*c1.r);sort(ans.begin(),ans.end());for(qwq tmp:ans) printf("%.8lf %.8lf ",tmp.x,tmp.y);putchar('\n');
}
过圆外一点作圆的切线
圆外点 ppp,圆心和任意切点组成的直角三角形两边已知,可以求解其中一锐角并将直线旋转。
inline void query(qwq p,cir c){vector<qwq> ans;qaq l=get(p,c.p);double dis=len(p-c.p),t=asin(c.r/dis),d=sqrt(dis*dis-c.r*c.r);qwq d1=rotate(l.d,t),d2=rotate(l.d,pi*2-t);ans.push_back(p+d1*d),ans.push_back(p+d2*d);sort(ans.begin(),ans.end());for(qwq tmp:ans) printf("%.8lf %.8lf\n",tmp.x,tmp.y);
}
求两圆公切线
分内含/内切/相交/外切/外离五种情况考虑。也是利用一些简单的几何性质求解直角三角形,然后旋转得到交点。
代码求的是在圆 c1c_1c1 上的交点。
inline void solve(cir c1,cir c2){int flag=0;if(c1.r<c2.r) swap(c1,c2),flag=1;double dis=len(c1.p-c2.p);if(dis+c2.r<c1.r) return;//内含qaq l=get(c1.p,c2.p);if(fabs(c1.r-c2.r-dis)<eps){//内切qwq ans=c1.p+l.d*c1.r;return printf("%.10lf %.10lf\n",ans.x,ans.y),void();}vector<qwq> ans;double t=acos((c1.r-c2.r)/dis);qwq d1=rotate(l.d,t),d2=rotate(l.d,2*pi-t);if(flag) ans.pb(c2.p+d1*c2.r),ans.pb(c2.p+d2*c2.r);else ans.pb(c1.p+d1*c1.r),ans.pb(c1.p+d2*c1.r);if(fabs(dis-c1.r-c2.r)<eps) ans.pb(c1.p+l.d*c1.r);//外切else if(dis>c1.r+c2.r){//外离if(flag) swap(c1,c2),l=get(c1.p,c2.p);double xie=dis*c1.r/(c1.r+c2.r),t=acos(c1.r/xie);d1=rotate(l.d,t),d2=rotate(l.d,2*pi-t);ans.pb(c1.p+d1*c1.r),ans.pb(c1.p+d2*c1.r);}sort(ans.begin(),ans.end());for(qwq tmp:ans) printf("%.10lf %.10lf\n",tmp.x,tmp.y);
}
扇形面积与弓形面积
根据初中公式求解即可。注意这里算的都是圆心角 ≤π\le \pi≤π 的部分的面积。
inline double angle(qwq p1,qwq p2){return acos((p1*p2)/len(p1)/len(p2));
}
inline double sshan(cir c,qwq a,qwq b){double t=angle(a-c.p,b-c.p);return t/2*c.r*c.r;
}
inline double sgong(cir c,qwq a,qwq b){return sshan(c,a,b)-fabs((b-c.p)^(a-c.p)/2);
}
圆与圆面积交
特判内含/外离之后考虑处理相交。发现当圆心角在 π\piπ 以内的时候对答案的贡献为扇形面积减三角形面积,否则答案为扇形面积加三角形面积,但此时 sinθ\sin\thetasinθ 为负,依然正确。
inline double query(cir c1,cir c2){if(c1.r<c2.r) swap(c1,c2);double dis=len(c1.p-c2.p);if(dis>=c1.r+c2.r) return 0;if(c2.r+dis<=c1.r) return pi*c2.r*c2.r;double r1=c1.r*c1.r,r2=c2.r*c2.r;double t1=2*acos((dis*dis+r1-r2)/(2*dis*c1.r));double t2=2*acos((dis*dis+r2-r1)/(2*dis*c2.r));return t1/2*r1+t2/2*r2-r1*sin(t1)/2-r2*sin(t2)/2;
}
圆与多边形面积交
把多边形拆成多个由多边形上相邻两顶点和圆心组成的三角形,根据圆心与多边形的位置关系将每部分面积交标上正负符号,然后分类:
-
(当前正在讨论的多边形上的)两点全在圆内,答案为三角形面积;
-
两点全在圆外:
- 两点所成线段与圆没有交点,答案为扇形面积;
- 两点所成线段与圆有交点,答案为扇形面积减多余的弓形面积;
-
一点在圆内一点在圆外:答案为一个三角形面积 + 一个扇形面积。
inline qwq cirline(cir c,qaq l){qwq cz=l.d*((c.p-l.a)*l.d)+l.a;double dis=len(c.p-cz);return cz+l.d*sqrt(c.r*c.r-dis*dis);
}
inline bool check(qwq a,qwq b,cir c){return max(a.x,b.x)>=c.p.x-eps&&min(a.x,b.x)<=c.p.x+eps||max(a.y,b.y)>=c.p.y-eps&&min(a.y,b.y)<=c.p.y+eps;
}
inline double calc(cir c,qwq a,qwq b){double tmp=(a-c.p)^(b-c.p);if(fabs(tmp)<eps) return 0;int f=tmp>0?1:-1,f1=len(a-c.p)<=c.r,f2=len(b-c.p)<=c.r;if(f1&&f2) return tmp/2;qaq l=get(a,b);qwq cz=l.d*((c.p-l.a)*l.d)+l.a;double jl=len(c.p-cz);if(jl<c.r) tmp=sqrt(c.r*c.r-jl*jl);if(!f1&&!f2){qaq l1=get(c.p,a),l2=get(c.p,b);double s=sshan(c,l1.a+l1.d*c.r,l2.a+l2.d*c.r);if(jl<c.r&&check(a,b,c)) s-=sgong(c,cz-l.d*tmp,cz+l.d*tmp);return s*f;}if(!f1) swap(a,b),l=get(a,b);qwq p1=cirline(c,l),p2=cirline(c,get(c.p,b));double s=fabs((c.p-a)^(p1-a)/2)+sshan(c,p1,p2);return s*f;
}
inline double query(){a[n+1]=a[1];double ans=0;rep(i,1,n) ans+=calc(c,a[i],a[i+1]);return fabs(ans);
}
杂项
曼哈顿距离与切比雪夫距离
平面上两点 (x1,y1)(x_1,y_1)(x1,y1) 和 (x2,y2)(x_2,y_2)(x2,y2),它们的曼哈顿距离为 ∣x1−x2∣+∣y1−y2∣|x_1-x_2|+|y_1-y_2|∣x1−x2∣+∣y1−y2∣,切比雪夫距离为 max(∣x1−x2∣,∣y1−y2∣)\max(|x_1-x_2|,|y_1-y_2|)max(∣x1−x2∣,∣y1−y2∣)。
- 曼哈顿距离 ⇒\Rightarrow⇒ 切比雪夫距离:(x,y)⇒(x+y,x−y)(x,y)\Rightarrow(x+y,x-y)(x,y)⇒(x+y,x−y);
- 切比雪夫距离 ⇒\Rightarrow⇒ 曼哈顿距离:(x,y)⇒(x+y2,x−y2)(x,y)\Rightarrow(\dfrac{x+y}{2},\dfrac{x-y}{2})(x,y)⇒(2x+y,2x−y)。
相关文章:

二维计算几何全家桶
参考文章:范神的神仙博客 前置芝士 一些高中数学 向量的叉积:向量的点积为 a⋅b∣a∣∣b∣cos<a,b>a\cdot b|a||b|\cos<a,b>a⋅b∣a∣∣b∣cos<a,b>,向量的叉积为 ab∣a∣∣b∣sin<a,b>a\times b|a||b|\sin<…...
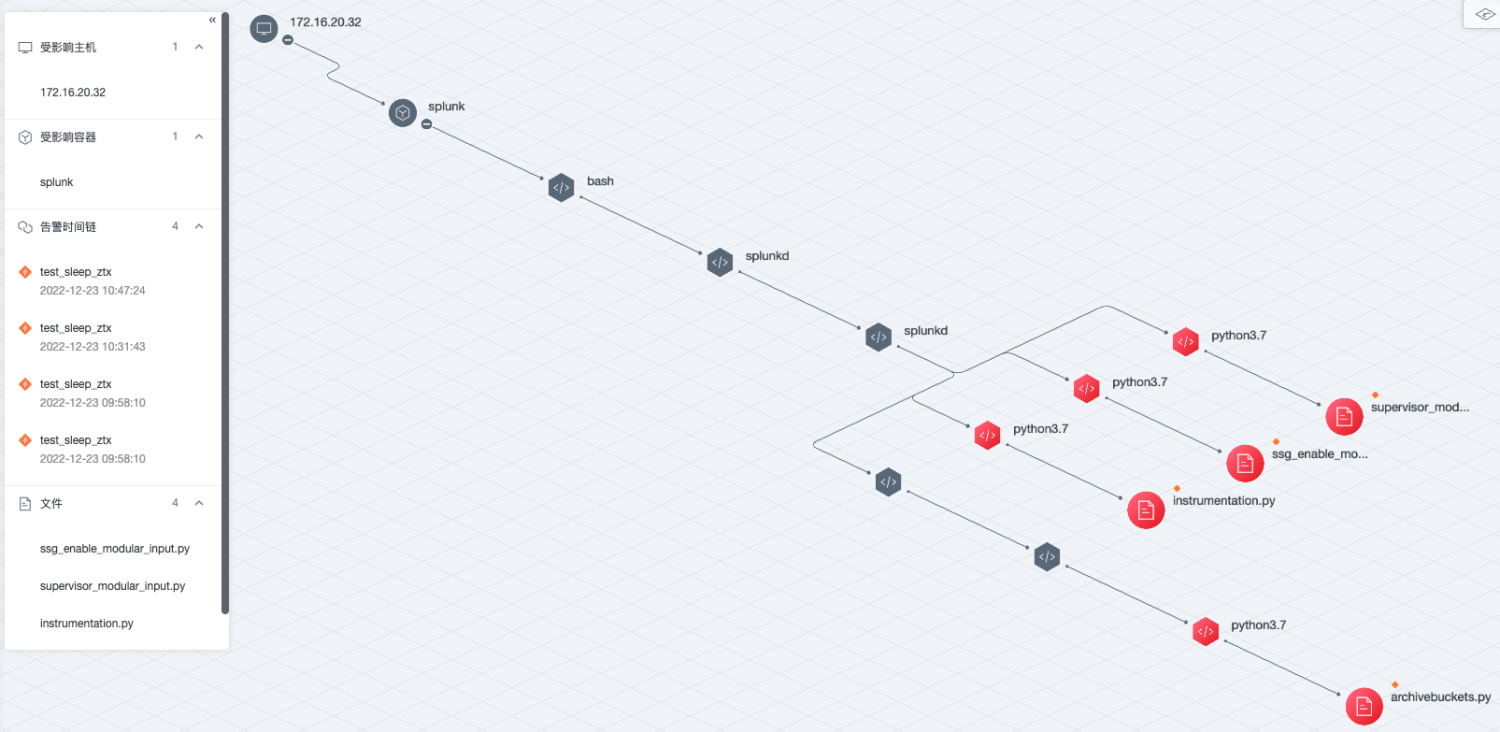
基于图的下一代入侵检测系统
青藤云安全是一家主机安全独角兽公司,看名字就知道当前很大一块方向专注云原生应用安全,目前主营的是主机万相/容器蜂巢产品,行业领先,累计支持 800万 Agent。当前公司基于 NebulaGraph 结合图技术开发的下一代实时入侵检测系统已…...

若依框架---树状层级部门数据库表
👏作者简介:大家好,我是小童,Java开发工程师,CSDN博客博主,Java领域新星创作者 📕系列专栏:前端、Java、Java中间件大全、微信小程序、微信支付、若依框架、Spring全家桶 Ǵ…...
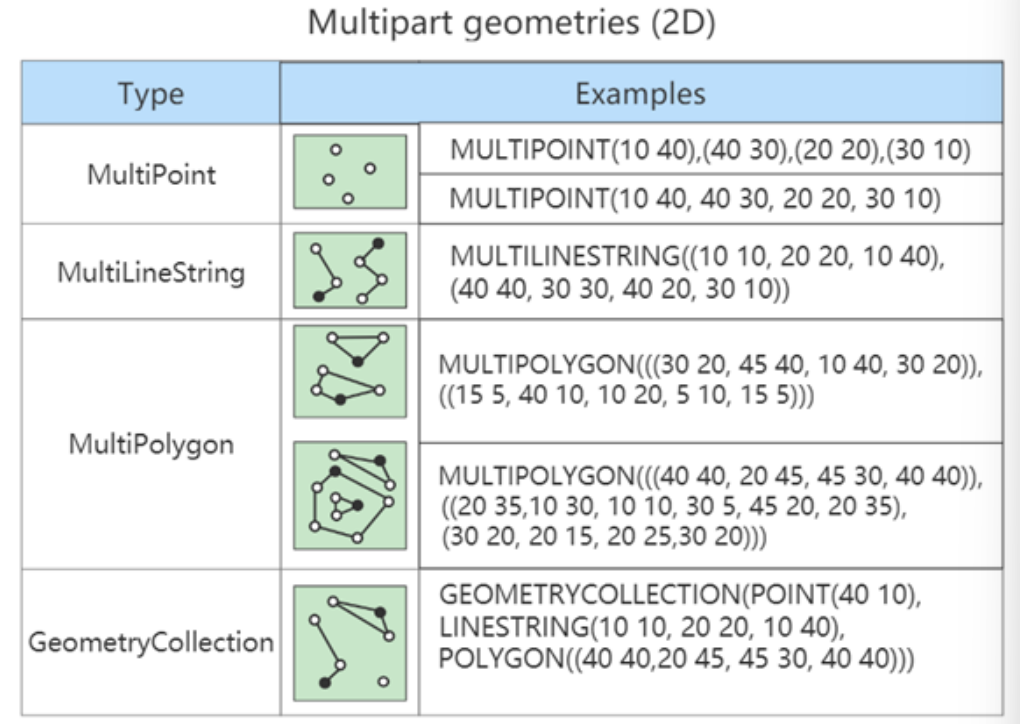
【Mysql第十期 数据类型】
文章目录1. MySQL中的数据类型2.类型介绍2.2 可选属性2.2.2 UNSIGNED2.2.3 ZEROFILL2.3 适用场景2.4 如何选择?3. 浮点类型3.2 数据精度说明3.3 精度误差说明4. 定点数类型4.1 类型介绍4.2 开发中经验5. 位类型:BIT6. 日期与时间类型6.1 YEAR类型6.2 DAT…...

2023-2-9 刷题情况
删除子文件夹 题目描述 你是一位系统管理员,手里有一份文件夹列表 folder,你的任务是要删除该列表中的所有 子文件夹,并以 任意顺序 返回剩下的文件夹。 如果文件夹 folder[i] 位于另一个文件夹 folder[j] 下,那么 folder[i] 就…...
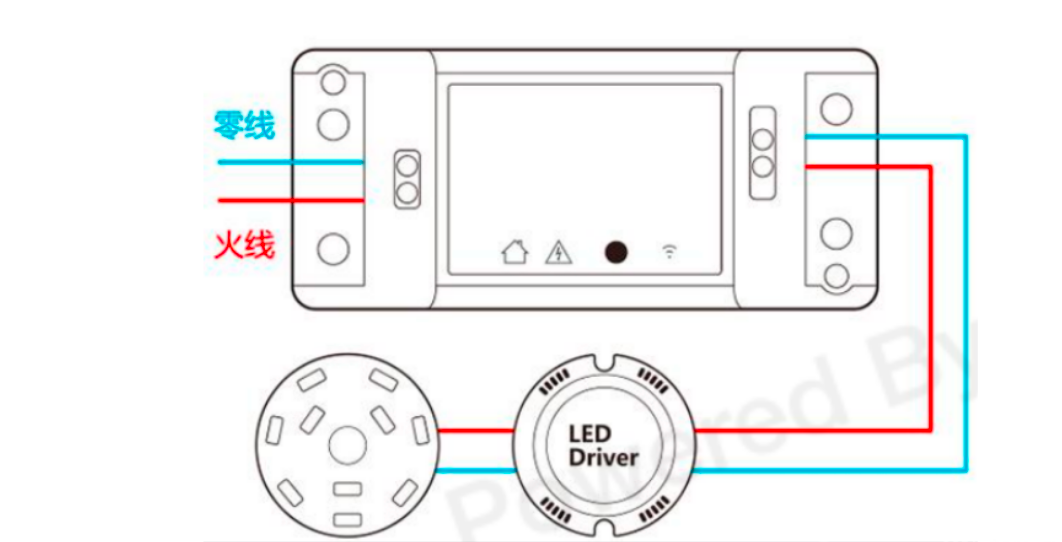
Homekit智能家居DIY设备-智能通断开关
智能通断器,也叫开关模块,可以非常方便地接入家中原有开关、插座、灯具、电器的线路中,通过手机App或者语音即可控制电路通断,轻松实现原有家居设备的智能化改造。 随着智能家居概念的普及,越来越多的人想将自己的家改…...
概述)
【java】EJB(Enterprise Java Bean)概述
EJB概述目录一、什么情况下需要企业Bean需要使用EJB的N个理由二、EJB的基本分类2.1、Enterprise Bean2.2、 Message Driven Bean(MDB)——消息驱动Bean,基于JMS三、定义客户端访问的接口3.1、 远程客户端——客户端与其调用的EJB对象不在同一个JVM进程中3.2、本地客户端——客户…...

Android 10.0 Launcher3桌面禁止左右滑动
1.1概述 在10.0的rom定制化开发中,由于Launcher3有一些功能需要定制,这样的需求也好多的,现在功能需求要求桌面固定在Launcher3的app列表页,不让左右移动,就是禁止左右移动的功能实现,所以需要禁止滑动分析页面滑动部分的功能,然后禁用 2.1Launcher3桌面禁止左右滑动的核…...

日期类的实现
文章目录1. 日期类的具体实现1.查询当前月份的天数2. 构造函数的实现(注意)3.d1d24. d1!d25. d1<d26. d1<d27. d1>d28. d1>d29. 日期天数10.日期天数11.日期-天数12. 日期-天数13. d和 d14. --d 和 d--15.日期日期 返回天数2. 函数的声明——date.h3. 函数的定义—…...

2022年这5款熟悉的软件退出了历史舞台
在过去的一年里,有很多新产品发布,当然也有很多产品与我们就此别过。这些产品曾陪伴我们的生活,给我们带来欢乐,帮助我们成长。所以本文将盘点一下在2022年和我们告别的产品。1.微软IE浏览器IE浏览器1995年8月16日正式上线&#x…...
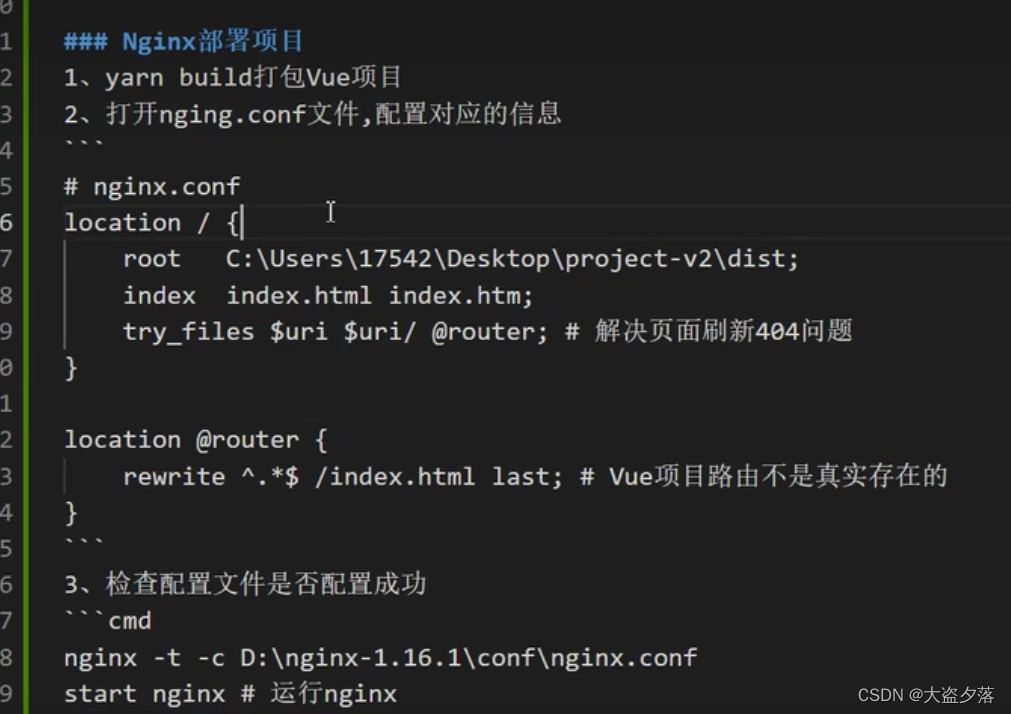
用Nginx打包部署vue3项目及404和500解决
打包vue3 npm run build安装Nginx 这里安装步骤比较繁琐,现在服务器比较便宜,如果想用Nginx,可以去菜鸟教程https://www.runoob.com/linux/nginx-install-setup.html 配置安装一下找到安装路径下的 conf 文件夹 下 nginx.conf文件࿰…...

Java面试——多线程并发篇
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...
维基百科数据抽取
1. 数据路径 https://dumps.wikimedia.org/enwiki/latest/ ----英文 https://dumps.wikimedia.org/zhwiki/latest/ ----中文 https://dumps.wikimedia.org/enwiki/latest/enwiki-latest-pages-articles.xml.bz2 --下载最新的 https://dumps.wikimedia.org/wikidatawiki/2023…...
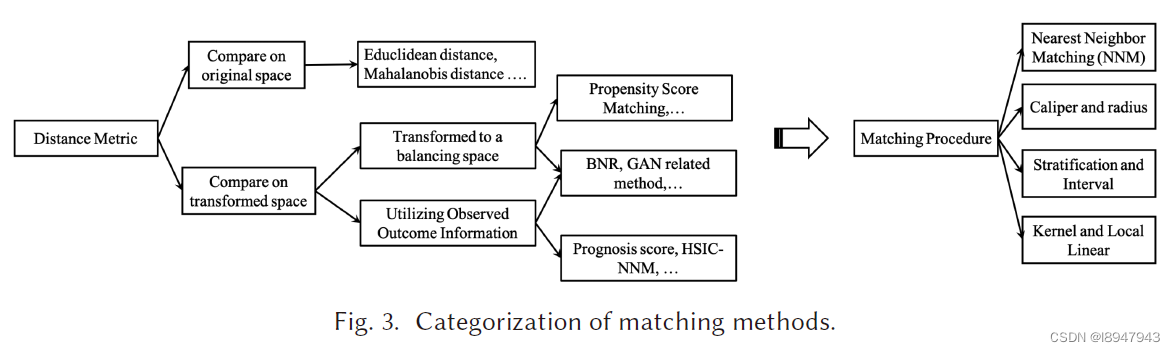
2020年因果推断综述《A Survey on Causal Inference》
最近阅读了TKDD2020年的《A Survey on Causal Inference》,传送门,自己对文章按照顺序做了整理,同时对优秀的内容进行融合,如有不当之处,请多多指教。 文章对因果推理方法进行了全面的回顾,根据传统因果框…...

嵌入式linux系统测试程序编写
文章目录 网络CPU load监测性能设定开源测试工具iozone —— 文件系统测试工具iperf —— 网络性能测试工具LMbench —— 系统性能评测LTP —— linux功能/性能压力测试memtester —— 内存测试,坏位检测stressapptest —— 内存流量压力测试stream —— 内存性能测试fio ——…...

力扣SQL刷题5
目录597. 好友申请 I:总体通过率602. 好友申请 II :谁有最多的好友603. 连续空余座位1045. 买下所有产品的客户597. 好友申请 I:总体通过率 官方讲的题目太繁琐了,大概就是(表2中列1列2不全相同的行数)/&a…...

动态规划详解(完结篇)——如何抽象出动态规划算法?以及解题思路
今天直接开始讲解FIRST:如何抽象出动态规划算法?这个问题,困扰了无数代OIER,包括本蒟蒻在比赛的时候,看一道题,怎么想到他是什么算法的呢?这就需要抽象能力而不同的算法,往往有着不同…...
C语言一维数组篇【下】——每日刷题经验分享
一维数组篇——每日刷题经验分享~😎前言🙌有序序列插入一个整数 😊序列中删除指定数字 😊序列中整数去重小乐乐查找数字筛选法求素数总结撒花💞😎博客昵称:博客小梦~ 😊最喜欢的座右…...

VHDL语言基础-组合逻辑电路-其它组合逻辑模块
目录 多路选择器: 逻辑功能: 常用的类型: 4选1多路选择器的实现: 求补器: 求补器的实现: 三态门: 三态门的应用实例: 三态门的实现: 缓冲器: 什么是…...

初识Vue
文章目录1. 前言2. Vue 的特点3. 安装 Vue4. HelloWord1. 前言 vue是什么 ? 引用 : vue.js 文档 Vue (读音 /vjuː/,类似于 view) 是一套用于构建用户界面的渐进式框架。与其它大型框架不同的是,Vue 被设计为可以自底向上逐层…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...
