LA@相似方阵和对角化
文章目录
- 相似方阵
- 相似矩阵和特征值
- 小结
- 方阵相似对角化
- 结论
- 推论
- 对角化方法归纳
- 例
- 方阵高次幂
相似方阵
- 对角阵是矩阵中最简单的一类矩阵
- 对角阵相关的乘法运算是很高效的
- 相似方阵是和对角阵相关的概念
- 设A和B是n阶方阵,如果存在n阶可逆方阵P,使得P−1AP=BP^{-1}AP=BP−1AP=B,则称方阵A,B相似,记为A∼BA\sim{B}A∼B
- 该定义可以用来判断给定的两个方阵是否相似
- 也可以根据给定的方阵A来生成与A相似的矩阵集
- 相似矩阵特点
- A∼AA\sim{A}A∼A
- A∼B⇒B∼AA\sim{B}\Rightarrow{B\sim{A}}A∼B⇒B∼A
- P−1AP=B,A=PBP−1P^{-1}AP=B,A=PBP^{-1}P−1AP=B,A=PBP−1
- A∼B,B∼C⇒A∼CA\sim{B},B\sim{C}\Rightarrow{A\sim{C}}A∼B,B∼C⇒A∼C
- P−1AP=B,Q−1BQ=CP^{-1}AP=B,Q^{-1}BQ=CP−1AP=B,Q−1BQ=C
- QCQ−1=B=P−1APQCQ^{-1}=B=P^{-1}APQCQ−1=B=P−1AP
- PQCQ−1P−1=APQCQ^{-1}P^{-1}=APQCQ−1P−1=A
- (PQ)−1=Q−1P−1(PQ)^{-1}=Q^{-1}P^{-1}(PQ)−1=Q−1P−1
- 因此C∼AC\sim{A}C∼A
- 单位矩阵只和自身相似
- 设方阵A和单位阵E相似
- P−1AP=EP^{-1}AP=EP−1AP=E
- A=PEP−1=EA=PEP^{-1}=EA=PEP−1=E
- 因此和单位阵E相似的矩阵是E本身
相似矩阵和特征值
-
设A∼BA\sim{B}A∼B,即存在可逆阵P,P−1AP=BP^{-1}AP=BP−1AP=B
-
相似矩阵有相同的特征矩阵(因此有相同的特征值)
- 证明:
- f(λ)=∣λE−B∣=∣λE−P−1AP∣f(\lambda)=|\lambda{E}-B|=|\lambda{E}-P^{-1}AP|f(λ)=∣λE−B∣=∣λE−P−1AP∣
- =∣λ(P−1P)−P−1AP∣=|\lambda{(P^{-1}P)-P^{-1}AP}|=∣λ(P−1P)−P−1AP∣
- =∣P−1(λP−AP)∣=|P^{-1}(\lambda{P}-AP)|=∣P−1(λP−AP)∣
- =∣P−1(λE−A)P∣=|P^{-1}(\lambda{E}-A)P|=∣P−1(λE−A)P∣
- =∣P−1∣∣λE−A∣∣P∣=|P^{-1}||\lambda{E}-A||P|=∣P−1∣∣λE−A∣∣P∣
- =∣P∣−1∣P∣∣λE−A∣=|P|^{-1}|P||\lambda{E}-A|=∣P∣−1∣P∣∣λE−A∣
- =∣λE−A∣=|\lambda{E}-A|=∣λE−A∣
- 可见,A,B具有相同的特征方程,也具有共同的特征值
- f(λ)=∣λE−B∣=∣λE−P−1AP∣f(\lambda)=|\lambda{E}-B|=|\lambda{E}-P^{-1}AP|f(λ)=∣λE−B∣=∣λE−P−1AP∣
- 但是,特征值相同的方阵未必相似
- 证明:
-
∣A∣=∣B∣|A|=|B|∣A∣=∣B∣
- ∣B∣=∣P−1BP∣=∣P−1∣∣B∣∣P∣=∣P∣−1∣P∣∣B∣=B|B|=|P^{-1}BP|=|P^{-1}||B||P|=|P|^{-1}|P||B|=B∣B∣=∣P−1BP∣=∣P−1∣∣B∣∣P∣=∣P∣−1∣P∣∣B∣=B
-
tr(A)=tr(B)tr(A)=tr(B)tr(A)=tr(B)
- A,B具有相同的特征值
- tr(A)=∑i=1naii=∑i=1nλitr(A)=\sum\limits_{i=1}^{n}a_{ii}=\sum\limits_{i=1}^{n}\lambda_{i}tr(A)=i=1∑naii=i=1∑nλi
- tr(B)=∑i=1nbii=∑i=1nλitr(B)=\sum\limits_{i=1}^{n}b_{ii}=\sum\limits_{i=1}^{n}\lambda_{i}tr(B)=i=1∑nbii=i=1∑nλi
- ∴tr(A)=tr(B)\therefore tr(A)=tr(B)∴tr(A)=tr(B)
-
r(A)=r(B)r(A)=r(B)r(A)=r(B)
- A=P−1BPA=P^{-1}BP^{}A=P−1BP
- P,P−1P,P^{-1}P,P−1都是可逆矩阵,它们都可以表示为一系列的初等矩阵的乘积
- 因此,A相当于有B经过初等变换得到的等价矩阵,它们的秩相等(初等变换不改变秩)
- A=P−1BPA=P^{-1}BP^{}A=P−1BP
-
AT∼BTA^T\sim{B^T}AT∼BT
- P−1AP=BP^{-1}AP=BP−1AP=B
- Q−1BQ=AQ^{-1}BQ=AQ−1BQ=A
- (P−1AP)T=BT(P^{-1}AP)^T=B^T(P−1AP)T=BT
- PTAT(P−1)T=BTP^TA^T(P^{-1})^T=B^TPTAT(P−1)T=BT
- PTAT(PT)−1=BTP^TA^T(P^{T})^{-1}=B^TPTAT(PT)−1=BT
- 可见AT∼BTA^T\sim{B^T}AT∼BT
-
Am∼BmA^m\sim{B^m}Am∼Bm
- Bm=(P−1AP)m=(P−1AP)(P−1AP)⋯(P−1AP)B^m=(P^{-1}AP)^m=(P^{-1}AP)(P^{-1}AP)\cdots{(P^{-1}AP)}Bm=(P−1AP)m=(P−1AP)(P−1AP)⋯(P−1AP)
- =P−1A(PP−1)A(P⋯P−1)AP=P^{-1}A(PP^{-1})A(P\cdots{P^{-1})AP}=P−1A(PP−1)A(P⋯P−1)AP
- =P−1AmP=P^{-1}A^mP=P−1AmP
- P−1AmP=BmP^{-1}A^mP=B^mP−1AmP=Bm
- Bm=(P−1AP)m=(P−1AP)(P−1AP)⋯(P−1AP)B^m=(P^{-1}AP)^m=(P^{-1}AP)(P^{-1}AP)\cdots{(P^{-1}AP)}Bm=(P−1AP)m=(P−1AP)(P−1AP)⋯(P−1AP)
-
若A−1A^{-1}A−1存在,则B−1B^{-1}B−1存在,A−1∼B−1,A∗∼B∗A^{-1}\sim{B^{-1}},A^*\sim{B^*}A−1∼B−1,A∗∼B∗
-
B可逆:
- 方法1:
- A∼B⇒∣A∣=∣B∣=kA\sim{B}\Rightarrow{|A|=|B|}=kA∼B⇒∣A∣=∣B∣=k
- A−1A^{-1}A−1存在,∣A∣≠0|A|\neq{0}∣A∣=0,则∣B∣=∣A∣≠0|B|=|A|\neq{0}∣B∣=∣A∣=0
- 方法2:
- 由于A可逆,则P−1AP=BP^{-1}AP=BP−1AP=B表明,B是可逆矩阵的乘积,所以B也可逆
-
A−1=PB−1P−1A^{-1}=PB^{-1}P^{-1}A−1=PB−1P−1,因此B−1∼A−1B^{-1}\sim{A^{-1}}B−1∼A−1
- 设P−1A−1P=B−1P^{-1}A^{-1}P=B^{-1}P−1A−1P=B−1
- A−1=1∣A∣A∗=k−1A∗A^{-1}=\frac{1}{|A|}A^*=k^{-1}A^*A−1=∣A∣1A∗=k−1A∗
- B−1=1∣B∣B∗=k−1B∗B^{-1}=\frac{1}{|B|}B^{*}=k^{-1}B^*B−1=∣B∣1B∗=k−1B∗
- P−1k−1A∗P=k−1B∗P^{-1}k^{-1}A^*P=k^{-1}B^*P−1k−1A∗P=k−1B∗
- P−1A∗P=B∗P^{-1}A^*P=B^*P−1A∗P=B∗
- 设P−1A−1P=B−1P^{-1}A^{-1}P=B^{-1}P−1A−1P=B−1
-
小结
- 上述结论说明,相似阵之间有很多共同点
方阵相似对角化
-
如果方阵A∼BA\sim{B}A∼B,且B是一个对角阵(方阵),则称A可以相似对角化
- 简单的记为A∼ΛA\sim{\Lambda}A∼Λ;P−1AP=ΛP^{-1}AP=\LambdaP−1AP=Λ
-
不是所有方阵都可以对角化
-
n阶方阵A有n个线性无关向量是A和一个对角阵相似的充要条件
-
证明
-
设A和一个对角阵相似,则存在可逆阵PPP,使得$P^{-1}AP=\Lambda $
-
Λ=diag(λ1,⋯,λn)\Lambda=diag(\lambda_1,\cdots,\lambda_n)Λ=diag(λ1,⋯,λn)
-
AP=PΛAP=P\Lambda{}AP=PΛ
-
设可逆矩阵P=(α1,⋯,αn)P=(\alpha_1,\cdots,\alpha_n)P=(α1,⋯,αn)
-
则
-
PΛ=(α1,⋯,αn)(λ1λ2⋱λn)=(λ1α1,⋯,λnαn)P\Lambda =(\alpha_1,\cdots,\alpha_n) \begin{pmatrix} {{\lambda _1}} & {} & {} & {} \cr {} & {{\lambda _2}} & {} & {} \cr {} & {} & \ddots & {} \cr {} & {} & {} & {{\lambda _n}} \cr \end{pmatrix} =(\lambda_{1}\alpha_1,\cdots,\lambda_n\alpha_n) PΛ=(α1,⋯,αn)λ1λ2⋱λn=(λ1α1,⋯,λnαn)
-
AP=A(α1,⋯,αn)=(Aα1,⋯,Aαn)AP=A(\alpha_1,\cdots,\alpha_n)=(A\alpha_1,\cdots,A\alpha_n) AP=A(α1,⋯,αn)=(Aα1,⋯,Aαn)
-
AP=PΛ(Aα1,⋯,Aαn)=(λ1α1,⋯,λnαn)Aαi=λiαiAP=P\Lambda \\ (A\alpha_1,\cdots,A\alpha_n) =(\lambda_{1}\alpha_1,\cdots,\lambda_n\alpha_n) \\ A\alpha_{i}=\lambda_{i}\alpha_i AP=PΛ(Aα1,⋯,Aαn)=(λ1α1,⋯,λnαn)Aαi=λiαi
-
λi,i=1,⋯,n\lambda_i,i=1,\cdots,nλi,i=1,⋯,n是矩阵A的n个特征值
-
PPP是可逆矩阵,P的列向量组α1,⋯,αn\alpha_1,\cdots,\alpha_nα1,⋯,αn线性无关(事实上有λi≠λj,if j≠i\lambda_i\neq{\lambda_{j}},\text{if }j\neq{i}λi=λj,if j=i)
-
因此,P的n个列向量就是方阵A的n个线性无关特征向量
-
-
-
设存在Φ=α1,⋯,αn\Phi=\alpha_1,\cdots,\alpha_nΦ=α1,⋯,αn是A的关于λ1,⋯,λn\lambda_1,\cdots,\lambda_nλ1,⋯,λn的线性无关特征向量
-
Aαi=λiαiA\alpha_{i}=\lambda_{i}\alpha_iAαi=λiαi,i=1,⋯,ni=1,\cdots,ni=1,⋯,n
-
(Aα1,⋯,Aαn)=A(α1,⋯,αn)=AP(λ1α1,⋯,λnαn)=(α1,⋯,αn)(λ1λ2⋱λn)=PΛ(A\alpha_1,\cdots,A\alpha_n)=A(\alpha_1,\cdots,\alpha_n)=AP \\ (\lambda_1\alpha_1,\cdots,\lambda_n\alpha_n) =(\alpha_1,\cdots,\alpha_n) \begin{pmatrix} {{\lambda _1}} & {} & {} & {} \cr {} & {{\lambda _2}} & {} & {} \cr {} & {} & \ddots & {} \cr {} & {} & {} & {{\lambda _n}} \cr \end{pmatrix} =P\Lambda (Aα1,⋯,Aαn)=A(α1,⋯,αn)=AP(λ1α1,⋯,λnαn)=(α1,⋯,αn)λ1λ2⋱λn=PΛ
- 两行式子相等AP=PΛAP=P\LambdaAP=PΛ
-
令方阵P=(Φ)P=(\Phi)P=(Φ),因为Φ\PhiΦ线性无关,所以r(Φ)=nr(\Phi)=nr(Φ)=n,方阵P可逆
- 对AP=PΛAP=P\LambdaAP=PΛ同时左乘P−1P^{-1}P−1
- P−1AP=ΛP^{-1}AP=\LambdaP−1AP=Λ
- 因此A∼ΛA\sim{\Lambda}A∼Λ
-
-
-
结论
- 通过上述推到,可以发现,如果方阵A可以对角化,那么
- A的n个线性无关向量组Ψ=(α1,⋯,αn)\Psi=(\alpha_1,\cdots,\alpha_n)Ψ=(α1,⋯,αn)构成的矩阵P=(Ψ)P=(\Psi)P=(Ψ)
- A的对应于Ψ\PsiΨ的n个特征值λ1,⋯,λn\lambda_1,\cdots,\lambda_nλ1,⋯,λn构成的对角阵Λ=diag(λ1,⋯,λn)\Lambda=diag(\lambda_1,\cdots,\lambda_n)Λ=diag(λ1,⋯,λn)
- P,ΛP,\LambdaP,Λ恰好能够满足P−1AP=ΛP^{-1}AP=\LambdaP−1AP=Λ
推论
- 如果n阶方阵A存在n个互不相同的特征值,则A可以对角化
- 根据特征值的相关性质定理,可以判断这种情况下存在n个线性无关的特征向量,因之可以对角化
- 考虑到方阵可能有重特征根的情况,需要多一些步骤:
- 如果A对于一个kik_iki重特征根λi\lambda_iλi恰好有kik_iki个线性无关特征向量,是A可以对角化的充要条件
- 这意味着,方阵A要有n个线性无关的特征向量才可以对角化
对角化方法归纳
- 求出方阵A所有特征值
- 求解不同特征值λi\lambda_iλi对应的齐次线性方程(λiE−A)=0(\lambda_iE-A)=0(λiE−A)=0的基础解系
- 判断基础解系中包含的向量个数是否和特征值λi\lambda_iλi的重数一致
- 如果不一致,则A不可对角
- 如果所有特征值得重数kik_iki和对应(λiE−A)=0(\lambda_iE-A)=0(λiE−A)=0的基础解系向量个数一致,则可以对角化
- 如果可对角化,则需要求解出一个可逆矩阵P,使得P−1AP=ΛP^{-1}AP=\LambdaP−1AP=Λ
- 设A的n个线性无关特征向量为ϕ=α1,⋯,αn\phi=\alpha_1,\cdots,\alpha_nϕ=α1,⋯,αn,则P=(ϕ)(\phi)(ϕ)
- 利用P计算Λ=P−1AP\Lambda=P^{-1}APΛ=P−1AP,Λ=diag(λ1,⋯,λn)\Lambda=diag(\lambda_1,\cdots,\lambda_n)Λ=diag(λ1,⋯,λn)
例
-
A=(2−1−10−10021)∣λE−A∣=(λ−2)(λ+1)(λ−1)=0A=\begin{pmatrix} 2 & { - 1} & { - 1} \cr 0 & { - 1} & 0 \cr 0 & 2 & 1 \cr \end{pmatrix} \\ |\lambda{E}-A|=(\lambda-2)(\lambda+1)(\lambda-1)=0 A=200−1−12−101∣λE−A∣=(λ−2)(λ+1)(λ−1)=0
- λ1=2,λ2=−1,λ3=1\lambda_1=2,\lambda_2=-1,\lambda_3=1λ1=2,λ2=−1,λ3=1都是单个,显然可以对角化
-
(λ1E−A)x=0(\lambda_1{E}-A)x=0(λ1E−A)x=0
-
(2E−A)x=02E−A=(0110300−21)→(010001000)(2E-A)x=0 \\ 2E-A= \begin{pmatrix} 0 & 1 & 1 \cr 0 & 3 & 0 \cr 0 & { - 2} & 1 \cr \end{pmatrix} \to \begin{pmatrix} 0 & 1 & 0 \cr 0 & 0 & 1 \cr 0 & 0 & 0 \cr \end{pmatrix} (2E−A)x=02E−A=00013−2101→000100010
- x2=0x3=0x1可以是任意常数可以取基础解系为α=(1,0,0)Tx_2=0 \\x_3=0 \\ x_1可以是任意常数 \\ 可以取基础解系为\alpha=(1,0,0)^T x2=0x3=0x1可以是任意常数可以取基础解系为α=(1,0,0)T
-
-
(λ2E−A)x=0(\lambda_2E-A)x=0(λ2E−A)x=0
- (−E−A)x=0取基础解系α2=(0,−1,1)T(-E-A)x=0 \\取基础解系\alpha_2=(0,-1,1)^{T} (−E−A)x=0取基础解系α2=(0,−1,1)T
-
(λ3E−A)x=0(\lambda_3E-A)x=0(λ3E−A)x=0
- (E−A)x=0取基础解系α3=(1,0,1)T(E-A)x=0 \\取基础解系\alpha_3=(1,0,1)^T (E−A)x=0取基础解系α3=(1,0,1)T
-
P=(1010−10011)Λ=diag(2,−1,1)且满足Λ=P−1APP= \begin{pmatrix} 1 & 0 & 1 \cr 0 & { - 1} & 0 \cr 0 & 1 & 1 \cr \end{pmatrix} \\ \Lambda=diag(2,-1,1) \\且满足\Lambda=P^{-1}AP P=1000−11101Λ=diag(2,−1,1)且满足Λ=P−1AP
方阵高次幂
- 方阵高次幂的计算通常计算量比较大,但是如果方阵能够对角化,则可以简单计算
- 设AAA可以被对角化:存在可逆阵P,使得P−1AP=ΛP^{-1}AP=\LambdaP−1AP=Λ
- A=PΛP−1A=P\Lambda{P^{-1}}A=PΛP−1
- An=(PΛP−1)(PΛP−1)⋯(PΛP−1)A^n=(P\Lambda{P^{-1}})(P\Lambda{P^{-1}})\cdots(P\Lambda{P^{-1}})An=(PΛP−1)(PΛP−1)⋯(PΛP−1)
- =PΛ(P−1P)Λ(P−1P)Λ⋯Λ(P−1P)ΛP−1=P\Lambda{}(P^{-1}P)\Lambda{}(P^{-1}P)\Lambda\cdots \Lambda (P^{-1}P)\Lambda{P^{-1}}=PΛ(P−1P)Λ(P−1P)Λ⋯Λ(P−1P)ΛP−1
- =PΛnP−1=P\Lambda^{n}P^{-1}=PΛnP−1
- 而对角阵Λ\LambdaΛ的乘法(高次幂)运算比较简单
- 设AAA可以被对角化:存在可逆阵P,使得P−1AP=ΛP^{-1}AP=\LambdaP−1AP=Λ
相关文章:

LA@相似方阵和对角化
文章目录相似方阵相似矩阵和特征值小结方阵相似对角化结论推论对角化方法归纳例方阵高次幂相似方阵 对角阵是矩阵中最简单的一类矩阵 对角阵相关的乘法运算是很高效的相似方阵是和对角阵相关的概念 设A和B是n阶方阵,如果存在n阶可逆方阵P,使得P−1APBP^{-1}APBP−1APB,则称方阵…...
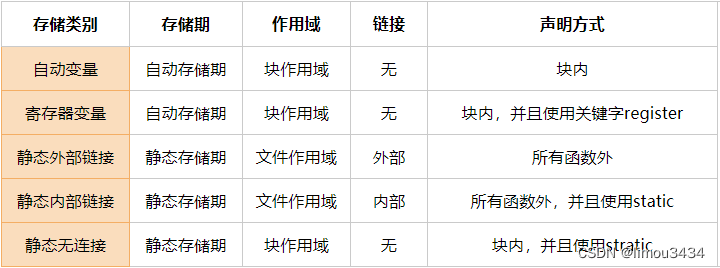
存储类别、链接与内存管理(二)
0、前言概要 本篇来自于我的另外一篇博客存储类别、链接与内存管理(一)的续篇,主要分析了C语言中的不同存储类别、关键字以及使用的注意事项 1、自动变量 (1)属性 自动存储期、块作用域、无连接 (2&a…...

JavaScript 入门教程||javascript 简介||JavaScript 用法
javascript 简介JavaScript 是互联网上最流行的脚本语言,这门语言可用于 HTML 和 web,更可广泛用于服务器、PC、笔记本电脑、平板电脑和智能手机等设备。JavaScript 是脚本语言JavaScript 是一种轻量级的编程语言。JavaScript 是可插入 HTML 页面的编程代…...

新闻稿写作指南
当你想要传达一则新闻,写一份新闻稿是非常必要的。新闻稿的目的是让读者了解某个事件或信息,以及提供与之相关的背景信息和重要细节。以下是新闻稿的写作指南,帮助你写出一份清晰、简洁、有价值的新闻稿。1、选择一个有新闻价值的主题你的新闻…...
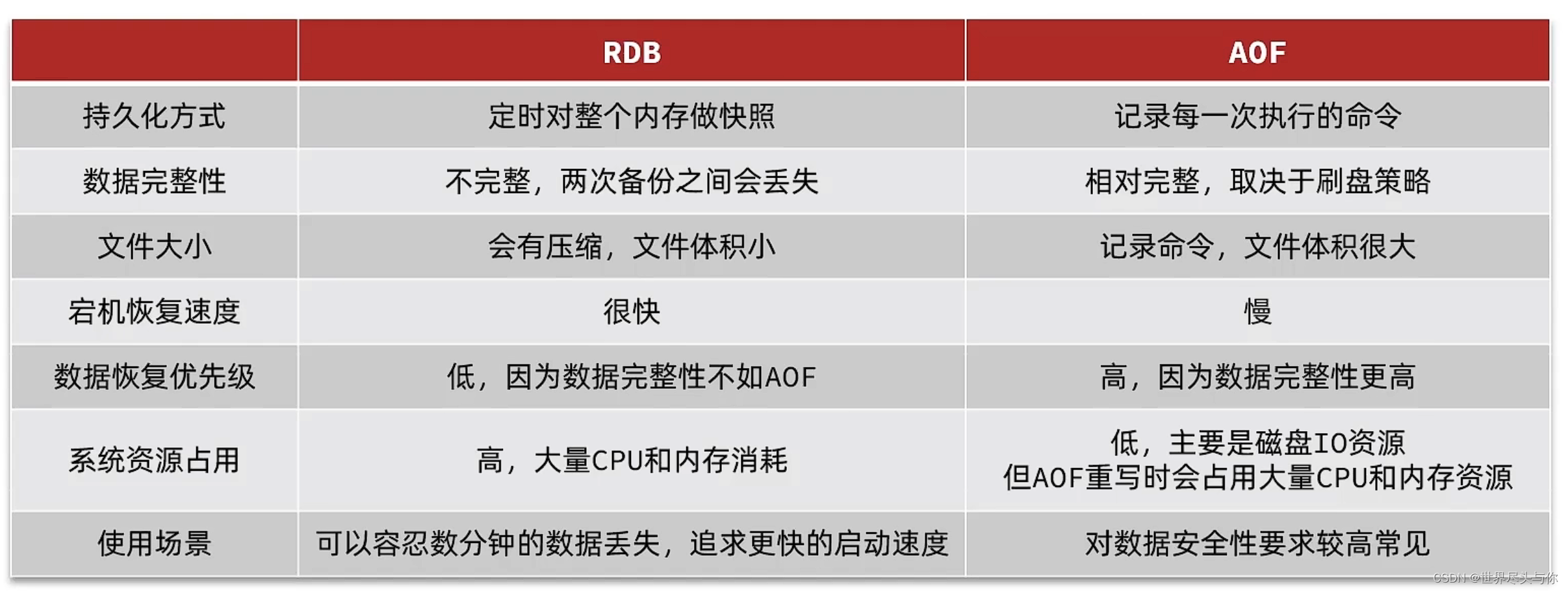
一文详解Redis持久化的两种方案
一文详解Redis持久化的两种方案1.RDB持久化2.RDB持久化原理3.AOF持久化4.RDB VS AOF1.RDB持久化 RDB全称Redis Database Backup file(Redis数据备份文件),也被叫做Redis数据快照。简单来说就是把内存中的所有数据都记录到磁盘中。当Redis实例故障重启后,…...
第六章 - 数据过滤where(where与and和or的组合用法)
第六章 - 数据过滤(where的用法)基本用法where的条件限制符等于号不等号! 或者<>小于<大于>小于等于<大于等于>between 的用法空值和非空值组合条件 and组合条件 orand 和 or 的计算次序in 和 not in基本用法 在查询语句中࿰…...

Oracle 定时任务例子
背景: 创建一个Oracle的定时任务,每天或指定时间 -----定义存储过程 create or replace procedure AAA_BBB as begin insert into AAA select * from BBB; commit; end; ----------------创建定时任务 declare xjobid number; begin DBMS_JOB.SUBM…...

Android常用9种自动化测试框架对比,Appium有哪些优势?
随着移动终端的普及,手机应用越来越多,也越来越重要。 App的回归测试用例数量也越来越多,全量回归也越来越消耗时间。移动 APP自动化测试 的难点移动 APP的UI自动化测试长久以来一直是一个难点,难点在于UI的”变”, 变化导致自动化…...
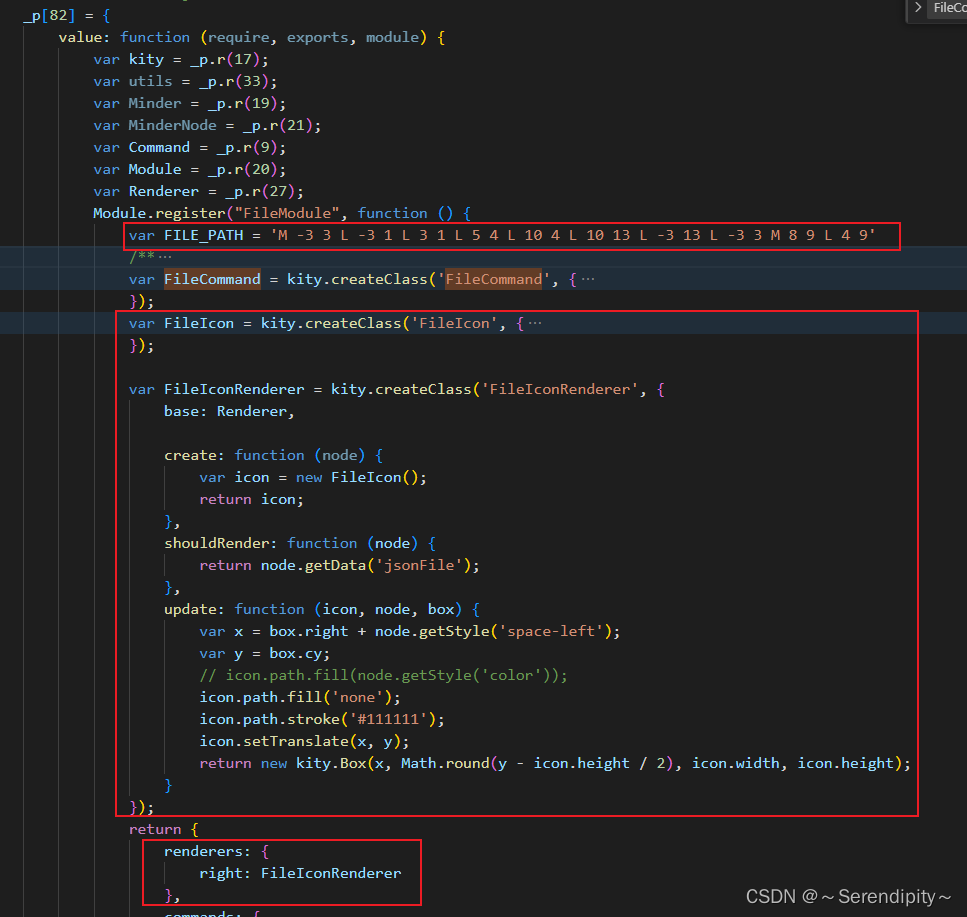
在vue2使用百度脑图的kityminder-core进行二次开发思维导图,给节点绑定数据后添加新的图标
需求说明:在给某个节点绑定文件数据后,用户并不能一眼看出哪个节点上绑定了数据,因此需要在绑定文件数据后给节点上加一个图标用于标识。 添加图标 1、在kityminder-core/src/module/file.js文件中添加代码 (file.js文件如何添加…...
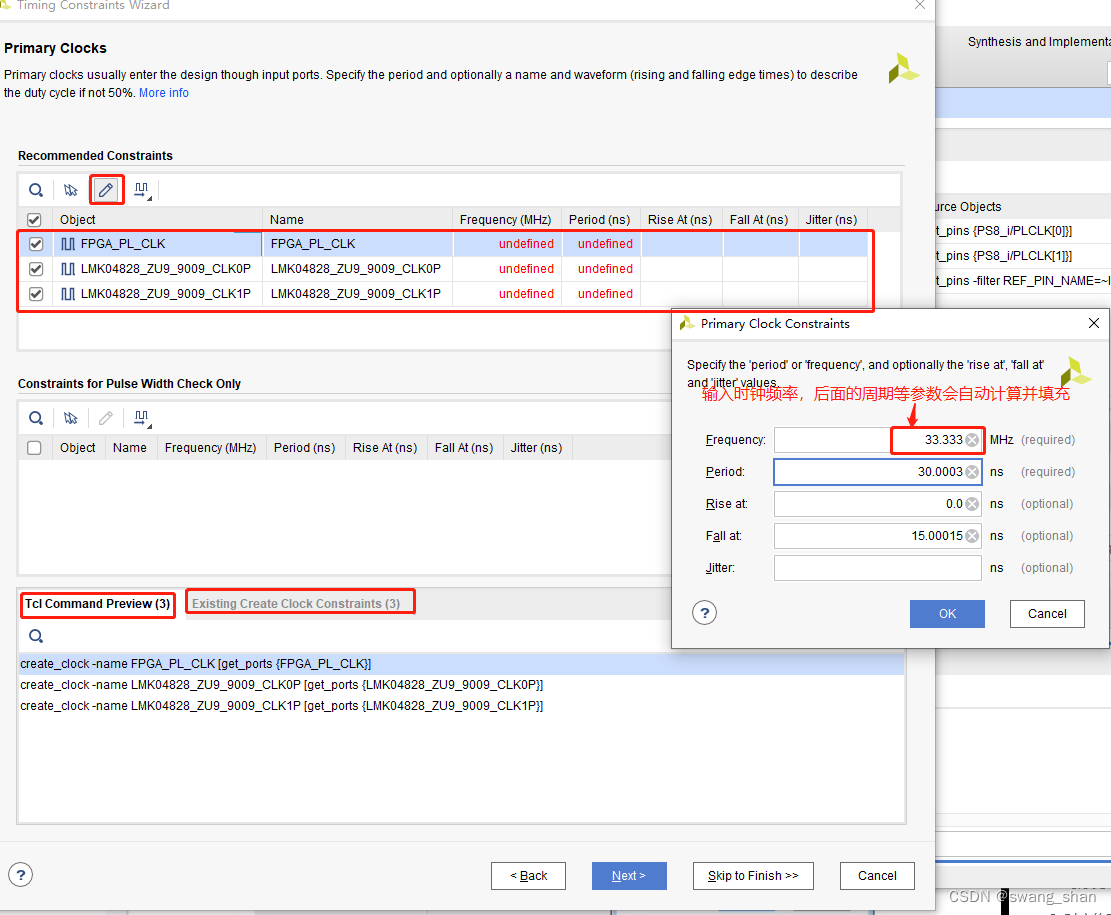
FPGA时序约束与分析 --- 时序约束概述
本系列参考文献 — FPGA时序与约束分析-吴厚航 FPGA从综合到实现需要的过程如下:synth_design -> opt_design -> place-design -> phys_opt_design -> route_design 1、时序约束的理解 2、时序约束的基本路径 3、时序约束的步骤 4、时序约束的主要方法…...

2022——寒假总结
文章目录背景报名摸索结果总结背景 大一上学期,刚上大学没有尽快适应,什么都没有学到。 因为疫情,所以平时的测试以及期末都是线上进行的,就没怎么认真学,网课直接划水。 我的生活与学习很不平衡,还热衷于参…...

C++11 Lambda表达式
文章首发公众号:iDoitnow 为什么引入Lambda Lambda表达式是一个可以内联在我们代码中的函数,我们可以将他传递给另外一个函数。在没有引入Lambda表达式之前,当我们遇到需要对多个数据,按照同一规则进行操作的时候,创建…...

冰湖灾害遥感监测评价与模拟分析
查看原文>>>mp.weixin.qq.com/s?__bizMzAxNzcxMzc5MQ&mid2247582638&idx1&sna22a1697b16a5edc2b74cb1ccf011689&chksm9be29cbeac9515a8227460103ae1b9f280af688eab0ce5a43448f9fa7c9cab820c389fcdc031&token10630879&langzh_CN#rd【专家简介…...
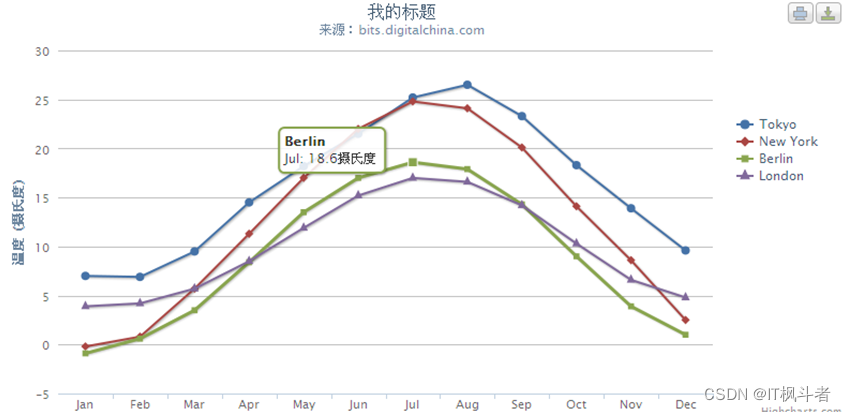
Highcharts.Chart
Highcharts 是一个使用javascript 脚本来生成图表的工具,和jfreechart 作用类似,都用来生成各种图表,并支持图片的导出和打印。 从官网 www.highcharts.com 上下载的压缩表中的example中有各种图表的例子。 要编写生成图表的例子建议从 文…...

遍历map的几种方法
#先往map加入几个数据 Map<Integer,String> mapnew HashMap<>(); map.put(1,"美好的周一"); map.put(2,"美好的周二"); map.put(3,"美好的周三"); 1 2 3 4 方法一:普通的foreach循环,…...

RocketMQ源码分析之Broker概述与同步消息发送原理与高可用设计及思考
1、Broker概述 Broker 在 RocketMQ 架构中的角色,就是存储消息,核心任务就是持久化消息,生产者发送消息给 Broker,消费者从 Broker 消费消息,其物理部署架构图如下: 备注:以上摘录自官方 RocketMQ 设计文档…...

K8s常见面试题总结
部分内容来自:k8s面试题大全(持续更新中) 目录 k8s常考面试题 1.1.什么是k8s? 1.2.简述Docker和Kubernetes的关系 1.3.k8s的组件有哪些,作用分别是什么? 1.4.简述kubelet的功能和作用 1.5.简述pod是…...

OpenFeign 自定义解码器Decoder 失效
问题描述 项目上开发了OpenFeign的自定义解码器,用来统一处理返回结果。 开发完后测试已经生效了,过两天后,这块代码没有变动的情况下,发现请求结果突然又不走自定义的解码器了。 代码如下 解码器 BaseResponseFeignDecoder …...

c++练习题8
1.在do-while循环中,循环由do开始,用while结束;必须注意的是:在while表达式后面的 不能丢,它表示do-while语句的结束。 A)0 B)1 C);…...

Python循环语句代码详解:while、for、break
目录 1 while循环 1 while循环 循环语句是程序设计中常用的语句之一。任何编程语言都有while循环,Python也不例外。while循环的格式如下所示。 while(表达式): … else: … while循环的执行过程:当循环表达式为真时,依次执行whi…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

【Linux系统】Linux环境变量:系统配置的隐形指挥官
。# Linux系列 文章目录 前言一、环境变量的概念二、常见的环境变量三、环境变量特点及其相关指令3.1 环境变量的全局性3.2、环境变量的生命周期 四、环境变量的组织方式五、C语言对环境变量的操作5.1 设置环境变量:setenv5.2 删除环境变量:unsetenv5.3 遍历所有环境…...

消防一体化安全管控平台:构建消防“一张图”和APP统一管理
在城市的某个角落,一场突如其来的火灾打破了平静。熊熊烈火迅速蔓延,滚滚浓烟弥漫开来,周围群众的生命财产安全受到严重威胁。就在这千钧一发之际,消防救援队伍迅速行动,而豪越科技消防一体化安全管控平台构建的消防“…...
