11 二阶矩方法和Lovasz局部引理
文章目录
- 11 二阶矩方法和Lovasz局部引理
- 11.1 The Second-Moment Method——二阶矩方法
- 11.1.1 二阶矩方法定理
- 11.1.2 二阶矩方法的应用——随机图阈值
- 11.2 Lovasz Local Lemma——Lovasz局部引理
- 11.2.1 LLL定理
- 11.2.2 LLL定理证明
- 11.3 Asymmetric LLL
11 二阶矩方法和Lovasz局部引理
11.1 The Second-Moment Method——二阶矩方法
11.1.1 二阶矩方法定理
首先写出二阶矩方法的定理:
- 若存在非负随机整数 X X X,则有:
P ( X = 0 ) ≤ V a r [ X ] ( E [ X ] ) 2 P(X = 0) \leq \frac{Var[X]}{{(E[X])}^2} P(X=0)≤(E[X])2Var[X]
证明:
P ( X = 0 ) ≤ P ( ∣ X − E [ X ] ∣ ≥ E [ X ] ) ≤ V a r [ X ] ( E [ X ] ) 2 P(X = 0) \leq P(|X-E[X]| \geq E[X]) \leq \frac{Var[X]}{{(E[X])}^2} P(X=0)≤P(∣X−E[X]∣≥E[X])≤(E[X])2Var[X]
11.1.2 二阶矩方法的应用——随机图阈值
二阶矩方法可以应用在,对随机图中的阈值进行概率求解。
首先了解一下什么是随机图中的阈值:
- 假设有一个图模型被定义为 G n , p G_{n, p} Gn,p,其中 n n n表示图的节点数量, p p p表示随机图的阈值。
- p p p的阈值表示为一个函数 f ( n ) f(n) f(n):在当 p > f ( n ) p>f(n) p>f(n)时,图 G n , p G_{n, p} Gn,p会拥有图的一些性质;当 p < f ( n ) p<f(n) p<f(n)时,图 G n , p G_{n, p} Gn,p不拥有这些性质。
在这里要补充一下(因为我是第一次实际用到这个知识):
- o ( n ) o(n) o(n)表示函数的上界,表示绝对不会到这个大小。
- ω ( n ) \omega(n) ω(n)表示函数的下界,表示函数一定更大。
下文中说 o ( 1 ) → 0 o(1) \rightarrow 0 o(1)→0就是这个原因,因为这并非表示 o ( 1 ) o(1) o(1),而是一定比 o ( 1 ) o(1) o(1)更小。
接下来我们给出关于随机图的一条定理:
-
在图 G n , p G_{n, p} Gn,p中,若在 p = f ( n ) = o ( n − 2 3 ) p = f(n) = o(n^{-\frac{2}{3}}) p=f(n)=o(n−32)且 n n n足够大的条件下。对于任意的 ε > 0 \varepsilon > 0 ε>0,使得:
P ( ∣ 顶点数大于4的团 ∣ ≥ 1 ) < ε P(|\text{顶点数大于4的团}| \geq 1) < \varepsilon P(∣顶点数大于4的团∣≥1)<ε -
若 p = f ( n ) = ω ( n − 2 3 ) p = f(n) = \omega(n^{-\frac{2}{3}}) p=f(n)=ω(n−32),其余条件不变的情况下,有:
P ( ∣ 顶点数大于4的团 ∣ ≥ 1 ) > 1 − ε P(|\text{顶点数大于4的团}| \geq 1) > 1 - \varepsilon P(∣顶点数大于4的团∣≥1)>1−ε
也可以写作:
P ( ∣ 顶点数大于4的团 ∣ = 0 ) < ε P(|\text{顶点数大于4的团}| = 0) < \varepsilon P(∣顶点数大于4的团∣=0)<ε
证明1:定理中 p = f ( n ) = o ( n − 2 3 ) p = f(n) = o(n^{-\frac{2}{3}}) p=f(n)=o(n−32)的情况:
-
图中取出4个顶点一共有 C n 4 C_n^4 Cn4中情况。假设我们通过 X i X_i Xi表示第 i i i种情况下,四个顶点组成的是否是团,可以表示为:
X i = { 1 if C i is a 4-clique 0 otherwise X_i = \begin{cases} 1 & \text{if $C_i$ is a 4-clique} \\ 0 & \text{otherwise} \end{cases} Xi={10if Ci is a 4-cliqueotherwise -
根据第一点我们可以知道 X = ∑ i = 1 C n 4 X i X = \sum_{i=1}^{C_n^4} X_i X=∑i=1Cn4Xi,同时因为一个四顶点的团有6条边,可得:
E [ X ] = C n 4 p 6 = O ( n 4 ) ⋅ o ( n − 4 ) = o ( 1 ) → 0 < ε E[X] = C_n^4 p^6 = O(n^4) \cdot o(n^{-4}) = o(1) \rightarrow 0 < \varepsilon E[X]=Cn4p6=O(n4)⋅o(n−4)=o(1)→0<ε -
又因为Markov Inequality有 P ( X ≥ 1 ) ≤ E [ X ] P(X \geq 1) \leq E[X] P(X≥1)≤E[X],可得:
P ( X ≥ 1 ) ≤ E [ X ] < ε P(X \geq 1) \leq E[X] < \varepsilon P(X≥1)≤E[X]<ε
证明2:定理中 p = f ( n ) = ω ( n − 2 3 ) p = f(n) = \omega(n^{-\frac{2}{3}}) p=f(n)=ω(n−32)的情况:
对于定理中 p = f ( n ) = ω ( n − 2 3 ) p = f(n) = \omega(n^{-\frac{2}{3}}) p=f(n)=ω(n−32)的情况,为了证明 P ( X = 0 ) < ε P(X = 0) < \varepsilon P(X=0)<ε,我们需要用到二阶矩定理,可以将问题转化为证明 P ( X = 0 ) ≤ V a r [ X ] ( E [ X ] ) 2 < ε P(X = 0) \leq \frac{Var[X]}{{(E[X])}^2} < \varepsilon P(X=0)≤(E[X])2Var[X]<ε。但是期望好求,方差不好求,所以我们要先引入一条定理:
定理:若 Y i , i ∈ [ 1 , m ] Y_i, i \in [1, m] Yi,i∈[1,m]表示0-1随机变量,且 Y = ∑ i = 1 m Y i Y = \sum_{i=1}^{m} Y_i Y=∑i=1mYi,可得
V a r [ Y ] ≤ E [ Y ] + ∑ 1 ≤ i , j ≤ m ; i ≠ j C o v ( Y i , Y j ) Var[Y] \leq E[Y] + \sum_{1 \leq i, j \leq m; i \neq j} Cov(Y_i, Y_j) Var[Y]≤E[Y]+1≤i,j≤m;i=j∑Cov(Yi,Yj)
证明:
对于随机变量序列可以做如下转换:
V a r [ Y ] = V a r [ ∑ i = 1 m Y i ] = ∑ i = 1 m V a r [ Y i ] + ∑ 1 ≤ i , j ≤ m ; i ≠ j C o v ( Y i , Y j ) Var[Y] = Var[\sum_{i=1}^{m} Y_i] = \sum_{i=1}^m Var[Y_i] + \sum_{1 \leq i, j \leq m; i \neq j} Cov(Y_i, Y_j) Var[Y]=Var[i=1∑mYi]=i=1∑mVar[Yi]+1≤i,j≤m;i=j∑Cov(Yi,Yj)因为方差的性质可得:
V a r [ Y i ] = E [ Y i 2 ] − E [ Y i ] 2 ≤ E [ Y i ] Var[Y_i] = E[Y_i^2] - {E[Y_i]}^2 \leq E[Y_i] Var[Yi]=E[Yi2]−E[Yi]2≤E[Yi]代入第一个公式就可得:
V a r [ Y ] ≤ ∑ i = 1 m E [ Y i ] + ∑ 1 ≤ i , j ≤ m ; i ≠ j C o v ( Y i , Y j ) = E [ Y ] + ∑ 1 ≤ i , j ≤ m ; i ≠ j C o v ( Y i , Y j ) \begin{align} Var[Y] &\leq \sum_{i=1}^m E[Y_i] + \sum_{1 \leq i, j \leq m; i \neq j} Cov(Y_i, Y_j) \\ &= E[Y] + \sum_{1 \leq i, j \leq m; i \neq j} Cov(Y_i, Y_j) \end{align} Var[Y]≤i=1∑mE[Yi]+1≤i,j≤m;i=j∑Cov(Yi,Yj)=E[Y]+1≤i,j≤m;i=j∑Cov(Yi,Yj)
-
根据方差的不等式定理,我们知道除了期望还要考虑协方差。我们已知协方差的计算公式为:
C o v ( X , Y ) = E [ X Y ] − E [ X ] E [ Y ] Cov(X, Y) = E[XY] - E[X]E[Y] Cov(X,Y)=E[XY]−E[X]E[Y] -
假如我们选取的点集(四个点)的情况表示为 { C 1 , C 2 , … , C C n 4 } {\lbrace C_1, C_2, \dots, C_{C_n^4} \rbrace} {C1,C2,…,CCn4},我们可以将协方差分为四类:
- 没有公共点:8个点,12条边, E [ X Y ] = C n 8 ⋅ p 12 = E [ X ] E [ Y ] = C n 4 ⋅ p 6 ⋅ C n 4 ⋅ p 6 E[XY] = C_n^8 \cdot p^{12} = E[X]E[Y] = C_n^4 \cdot p^6 \cdot C_n^4 \cdot p^6 E[XY]=Cn8⋅p12=E[X]E[Y]=Cn4⋅p6⋅Cn4⋅p6
- 有一个公共点:7个点,12条边, E [ X Y ] = C n 7 ⋅ p 12 = E [ X ] E [ Y ] = C n 4 ⋅ p 6 ⋅ C 4 1 C n − 4 3 ⋅ p 6 E[XY] = C_n^7 \cdot p^{12} = E[X]E[Y] = C_n^4 \cdot p^6 \cdot C_4^1 C_{n-4}^3 \cdot p^6 E[XY]=Cn7⋅p12=E[X]E[Y]=Cn4⋅p6⋅C41Cn−43⋅p6
- 有两个公共点:6个点,11条边, E [ X Y ] = C n 6 ⋅ p 11 > E [ X ] E [ Y ] = C n 4 ⋅ p 6 ⋅ C 4 2 C n 2 ⋅ p 6 E[XY] = C_n^6 \cdot p^{11} > E[X]E[Y] = C_n^4 \cdot p^6 \cdot C_4^2 C_n^2 \cdot p^6 E[XY]=Cn6⋅p11>E[X]E[Y]=Cn4⋅p6⋅C42Cn2⋅p6
- 有三个公共点:5个点,9条边, E [ X Y ] = C n 5 ⋅ p 9 > E [ X ] E [ Y ] = C n 4 ⋅ p 6 ⋅ C 4 3 C n 1 ⋅ p 6 E[XY] = C_n^5 \cdot p^{9} > E[X]E[Y] = C_n^4 \cdot p^6 \cdot C_4^3 C_n^1 \cdot p^6 E[XY]=Cn5⋅p9>E[X]E[Y]=Cn4⋅p6⋅C43Cn1⋅p6
-
因为 E [ X Y ] − E [ X ] E [ Y ] < E [ X Y ] E[XY] - E[X]E[Y] < E[XY] E[XY]−E[X]E[Y]<E[XY]恒成立,我们直接用 E [ X Y ] E[XY] E[XY],可以得到:
V a r [ Y ] ≤ E [ Y ] + ∑ 1 ≤ i , j ≤ m ; i ≠ j C o v ( Y i , Y j ) ≤ C n 4 ⋅ p 6 + C n 6 ⋅ p 11 + C n 5 ⋅ p 9 = O ( n 4 q 6 + n 6 q 11 + n 5 q 9 ) \begin{align} Var[Y] &\leq E[Y] + \sum_{1 \leq i, j \leq m; i \neq j} Cov(Y_i, Y_j) \\ &\leq C_n^4 \cdot p^6 + C_n^6 \cdot p^{11} + C_n^5 \cdot p^9 \\ &= O(n^4 q^6 + n^6 q^{11} + n^5 q^9) \end{align} Var[Y]≤E[Y]+1≤i,j≤m;i=j∑Cov(Yi,Yj)≤Cn4⋅p6+Cn6⋅p11+Cn5⋅p9=O(n4q6+n6q11+n5q9) -
代入公式 P ( X = 0 ) ≤ V a r [ X ] ( E [ X ] ) 2 P(X = 0) \leq \frac{Var[X]}{{(E[X])}^2} P(X=0)≤(E[X])2Var[X]可得:
P ( X = 0 ) ≤ V a r [ X ] ( E [ X ] ) 2 = O ( n 4 q 6 + n 6 q 11 + n 5 q 9 ) o ( n 4 q 6 ) 2 = O ( n − 4 q − 6 + n − 2 q − 1 + n − 3 q − 3 ) \begin{align} P(X = 0) &\leq \frac{Var[X]}{{(E[X])}^2} \\ &= \frac{O(n^4 q^6 + n^6 q^{11} + n^5 q^9)}{{o(n^4 q^6)}^2} \\ &= O(n^{-4} q^{-6} + n^{-2} q^{-1} + n^{-3} q^{-3}) \end{align} P(X=0)≤(E[X])2Var[X]=o(n4q6)2O(n4q6+n6q11+n5q9)=O(n−4q−6+n−2q−1+n−3q−3) -
当 p = f ( n ) = ω ( n − 2 3 ) p = f(n) = \omega(n^{-\frac{2}{3}}) p=f(n)=ω(n−32)时可得:
P ( X = 0 ) = o ( 1 + n − 4 / 3 + n − 1 ) = o ( 1 ) P(X = 0) = o(1 + n^{-4/3} + n^{-1}) = o(1) P(X=0)=o(1+n−4/3+n−1)=o(1)
11.2 Lovasz Local Lemma——Lovasz局部引理
11.2.1 LLL定理
在介绍定理之前,我们先介绍一下事件独立性的概念:
-
假定有一组事件 A 1 , A 2 , … , A n A_1, A_2, \dots, A_n A1,A2,…,An,他们发生的概率 P ( A i ) ≤ p < 1 P(A_i) \leq p < 1 P(Ai)≤p<1,如果他们互相独立,则有:
P ( ∩ i A i ˉ ) ≥ ( 1 − p ) n > 0 P(\cap_{i} {\bar {A_i}}) \geq {(1 - p)}^n > 0 P(∩iAiˉ)≥(1−p)n>0 -
与上条件相同,但事件之间相互不独立,则有:
P ( ∩ i A i ˉ ) ≥ 1 − ∑ P ( A i ) P(\cap_{i} {\bar {A_i}}) \geq 1 - \sum P(A_i) P(∩iAiˉ)≥1−∑P(Ai) -
对于独立的事件具有以下的性质:
P ( A ) = P ( A ∣ ∩ i ∈ [ 1 , N ] A i ) P(A) = P(A| \cap_{i \in [1, N]} A_i) P(A)=P(A∣∩i∈[1,N]Ai)
我们给LLL定理一个定义:
- 假设有一组事件 A 1 , A 2 , … , A n A_1, A_2, \dots, A_n A1,A2,…,An,满足 ∀ i , P ( A i ) ≤ p \forall i, P(A_i) \leq p ∀i,P(Ai)≤p,其中 A i A_i Ai与除了 d d d个事件之外的事件都相互独立,则有:
- 若 p d ≤ 1 4 pd \leq \frac{1}{4} pd≤41,则有 P ( ∩ i A i ˉ ) ≥ ( 1 − 2 p ) n > 0 P(\cap_{i} {\bar {A_i}}) \geq {(1 - 2p)}^n > 0 P(∩iAiˉ)≥(1−2p)n>0
- 若 p ( d + 1 ) ≤ 1 e p(d+1) \leq \frac{1}{e} p(d+1)≤e1,则有 P ( ∩ i A i ˉ ) ≥ ( 1 − 1 d + 1 ) n > 0 P(\cap_{i} {\bar {A_i}}) \geq {(1 - \frac{1}{d+1})}^n > 0 P(∩iAiˉ)≥(1−d+11)n>0
11.2.2 LLL定理证明
这里证明一下 p d ≤ 1 4 pd \leq \frac{1}{4} pd≤41的情况。
为了证明LLL,这里引入一条引理,就非常好证明LLL了:
- Lemma:对于任意一个集合 S ⊂ { A 1 , A 2 , … , A n } S \subset {\lbrace A_1, A_2, \dots, A_n \rbrace} S⊂{A1,A2,…,An},对于任意 A ∉ S A \notin S A∈/S,有:
P ( A ∣ ∩ j ∈ S A j ˉ ) ≤ 2 p P(A| \cap_{j \in S} {\bar {A_j}}) \leq 2p P(A∣∩j∈SAjˉ)≤2p
通过这条引理我吗就可以证明LLL定理了:
-
我们将LLL定理中的 P ( ∩ i A i ˉ ) P(\cap_{i} {\bar {A_i}}) P(∩iAiˉ)展开得:
P ( ∩ i A i ˉ ) = ( 1 − P ( A 1 ) ) ( 1 − P ( A 2 ∣ A 1 ˉ ) ) … ( 1 − P ( A i ∣ ∩ j < i A j ˉ ) ) P(\cap_{i} {\bar {A_i}}) = {(1-P(A_1))} {(1-P(A_2|{\bar {A_1}}))} \dots {(1-P(A_i|\cap_{j < i}{\bar {A_j}}))} P(∩iAiˉ)=(1−P(A1))(1−P(A2∣A1ˉ))…(1−P(Ai∣∩j<iAjˉ)) -
根据上文的Lemma可以知道:
{ P ( A 1 ) ≤ 2 p P ( A 2 ∣ A 1 ˉ ) ≤ 2 p … P ( A i ∣ ∩ j < i A j ˉ ) ≤ 2 p \begin{cases} P(A_1) \leq 2p \\ P(A_2|{\bar {A_1}}) \leq 2p \\ \dots \\ P(A_i|\cap_{j < i}{\bar {A_j}}) \leq 2p \\ \end{cases} ⎩ ⎨ ⎧P(A1)≤2pP(A2∣A1ˉ)≤2p…P(Ai∣∩j<iAjˉ)≤2p -
所以可以将公式转换为:
P ( ∩ i A i ˉ ) ≥ ( 1 − 2 p ) i = ( 1 − 2 p ) n P(\cap_{i} {\bar {A_i}}) \geq {(1-2p)}^i = {(1-2p)}^n P(∩iAiˉ)≥(1−2p)i=(1−2p)n
所以我们接下来主要证明上述Lemma
我们分成两种情况来讨论:
-
∣ S ∣ = 0 |S| = 0 ∣S∣=0:没有集合的情况下说明没有其他的事件,所以可得
P ( A ∣ ∅ ) = P ( A ) ≤ p ≤ 2 p P(A| \empty) = P(A) \leq p \leq 2p P(A∣∅)=P(A)≤p≤2p
得证 ∣ S ∣ = 0 |S| = 0 ∣S∣=0时刻 -
∣ S ∣ = k + 1 |S| = k+1 ∣S∣=k+1:我们假设引理适用于 ∣ S ∣ ≤ k |S| \leq k ∣S∣≤k的所有情况,通过数学归纳法证明 ∣ S ∣ = k + 1 |S| = k+1 ∣S∣=k+1时刻的情况。
第一种情况我们简单就证明了,核心就在第二种情况上,我们先来给第二种情况做一些定义:
- 根据LLL定理的条件已知 p d ≤ 1 4 pd \leq \frac{1}{4} pd≤41
- 我们假设有一个事件 A A A, S S S表示不包含事件 A A A的一个事件集合
- 根据与 A A A事件的相对独立性,我们将 S S S分成两部分: S i n d S^{ind} Sind表示 S S S中与 A A A相对独立的事件、 S d e p S^{dep} Sdep表示 S S S中与 A A A有依赖关系的事件
根据以上定义,再次分成两种情况:
-
当 ∣ S i n d ∣ = k + 1 |S^{ind}| = k+1 ∣Sind∣=k+1时,或者说是 S i n d = S S^{ind} = S Sind=S时,我们可得:
P ( A ∣ ∩ j ∈ S A j ˉ ) = P ( A ) ≤ p ≤ 2 p P(A| \cap_{j \in S} {\bar {A_j}}) = P(A) \leq p \leq 2p P(A∣∩j∈SAjˉ)=P(A)≤p≤2p
得证 ∣ S ∣ = k + 1 |S| = k+1 ∣S∣=k+1且 ∣ S i n d ∣ = k + 1 |S^{ind}| = k+1 ∣Sind∣=k+1的情况 -
当 ∣ S i n d ∣ < k + 1 |S^{ind}| < k+1 ∣Sind∣<k+1时,我们可以通过Bayes Formula将 S S S通过条件概率的方式拆分开:
P ( A ∣ ∩ j ∈ S A j ˉ ) = P ( A ∣ ∩ j ∈ S d e p A j ˉ , ∩ j ∈ S i n d A j ˉ ) = P ( A , ∩ j ∈ S d e p A j ˉ ∣ ∩ j ∈ S i n d A j ˉ ) P ( ∩ j ∈ S d e p A j ˉ ∣ ∩ j ∈ S i n d A j ˉ ) \begin{align} P(A| \cap_{j \in S} {\bar {A_j}}) &= P(A| \cap_{j \in S^{dep}} {\bar {A_j}}, \cap_{j \in S^{ind}} {\bar {A_j}}) \\ &= \frac{P(A, \cap_{j \in S^{dep}} {\bar {A_j}}| \cap_{j \in S^{ind}} {\bar {A_j}})}{P(\cap_{j \in S^{dep}} {\bar {A_j}}| \cap_{j \in S^{ind}} {\bar {A_j}})} \end{align} P(A∣∩j∈SAjˉ)=P(A∣∩j∈SdepAjˉ,∩j∈SindAjˉ)=P(∩j∈SdepAjˉ∣∩j∈SindAjˉ)P(A,∩j∈SdepAjˉ∣∩j∈SindAjˉ)
通过对条件的Bayes变换,我们可以分别将分子与分母求解出来:
-
分子:
P ( ∩ j ∈ S d e p A j ˉ ∣ ∩ j ∈ S i n d A j ˉ ) ≥ 1 − ∑ j ∈ S d e p P ( A j ∣ ∩ j ∈ S i n d A j ˉ ) ⏞ = P ( A j ) —独立 ⏟ P ( ∩ i A i ˉ ) ≥ 1 − ∑ P ( A i ) ≥ 1 − ∣ S d e p ∣ ⏟ p d ≤ 1 4 ⟹ ∣ S d e p ∣ = d ≤ 1 4 p ( 2 p ) ≥ 1 − 1 4 p ⋅ 2 p = 1 2 \begin{align} P(\cap_{j \in S^{dep}} {\bar {A_j}}| \cap_{j \in S^{ind}} {\bar {A_j}}) &\geq \underbrace{ 1 - \sum_{j\in S^{dep}} \overbrace{P(A_j| \cap_{j \in S^{ind}} {\bar {A_j}})}^{ =P(A_j) \text{—独立} } }_{P(\cap_{i} {\bar {A_i}}) \geq 1 - \sum P(A_i)} \\ &\geq 1 - \underbrace{|S^{dep}|}_{pd \leq \frac{1}{4} \implies |S^{dep}| = d \leq \frac{1}{4p}}(2p) \\ &\geq 1- \frac{1}{4p} \cdot 2p \\ &= \frac{1}{2} \\ \end{align} P(∩j∈SdepAjˉ∣∩j∈SindAjˉ)≥P(∩iAiˉ)≥1−∑P(Ai) 1−j∈Sdep∑P(Aj∣∩j∈SindAjˉ) =P(Aj)—独立≥1−pd≤41⟹∣Sdep∣=d≤4p1 ∣Sdep∣(2p)≥1−4p1⋅2p=21 -
分母:
P ( A , ∩ j ∈ S d e p A j ˉ ∣ ∩ j ∈ S i n d A j ˉ ) ≤ P ( A ∣ ∩ j ∈ S i n d A j ˉ ) ⏟ = P ( A ) —独立 ≤ p P(A, \cap_{j \in S^{dep}} {\bar {A_j}}| \cap_{j \in S^{ind}} {\bar {A_j}}) \leq \underbrace{P(A| \cap_{j \in S^{ind}} {\bar {A_j}})}_{=P(A) \text{—独立}} \leq p P(A,∩j∈SdepAjˉ∣∩j∈SindAjˉ)≤=P(A)—独立 P(A∣∩j∈SindAjˉ)≤p
由此可证在 ∣ S ∣ = k + 1 |S| = k+1 ∣S∣=k+1且 ∣ S i n d ∣ < k + 1 |S^{ind}| < k+1 ∣Sind∣<k+1的情况下:
P ( A ∣ ∩ j ∈ S A j ˉ ) = P ( A , ∩ j ∈ S d e p A j ˉ ∣ ∩ j ∈ S i n d A j ˉ ) P ( ∩ j ∈ S d e p A j ˉ ∣ ∩ j ∈ S i n d A j ˉ ) ≤ 2 p P(A| \cap_{j \in S} {\bar {A_j}}) = \frac{P(A, \cap_{j \in S^{dep}} {\bar {A_j}}| \cap_{j \in S^{ind}} {\bar {A_j}})}{P(\cap_{j \in S^{dep}} {\bar {A_j}}| \cap_{j \in S^{ind}} {\bar {A_j}})} \leq 2p P(A∣∩j∈SAjˉ)=P(∩j∈SdepAjˉ∣∩j∈SindAjˉ)P(A,∩j∈SdepAjˉ∣∩j∈SindAjˉ)≤2p
11.3 Asymmetric LLL
在上一节的LLL中,我们只用到了两个参数: p p p表示概率、 d d d表示临域的大小。上一节我们通过定义 p , d p,d p,d之间的关系求解了概率边界,我们自然会想要通过更普遍的方式求得概率边界。于是我们提出了Asymmetric LLL,下面我们做一个定义:
- Asymmetric LLL(非对称LLL):有一组事件表示为 A 1 , A 2 , … , A n A_1, A_2, \dots, A_n A1,A2,…,An,其中 S i ⊂ { A 1 , A 2 , … , A n } S_i \subset {\lbrace A_1, A_2, \dots, A_n \rbrace} Si⊂{A1,A2,…,An}表示一组与 A i A_i Ai相对独立的事件集合。假设存在一组变量 r 1 , … , r n ∈ [ 0 , 1 ) r_1, \dots, r_n \in [0, 1) r1,…,rn∈[0,1),且满足 ∀ i , P ( A i ) ≤ r i ∏ j ∉ S i ( 1 − r j ) \forall i, P(A_i) \leq r_i \prod_{j \notin S_i}(1-r_j) ∀i,P(Ai)≤ri∏j∈/Si(1−rj),则有
P ( ∩ i A i ˉ ) ≥ ∏ i ( 1 − r i ) P(\cap_{i} {\bar {A_i}}) \geq \prod_{i}(1-r_i) P(∩iAiˉ)≥i∏(1−ri)
这条定理本文就不做证明,但是这条定理是包含LLL的,我们可以做一个分析:
-
假设 r i = 1 d + 1 r_i = \frac{1}{d+1} ri=d+11,我们可以通过在LLL中的定义得到:
P ( A i ) ( d + 1 ) ≤ 1 e ⟹ P ( A i ) ≤ 1 d + 1 ⋅ 1 e ≤ 1 d + 1 ⋅ ( 1 − 1 d + 1 ) d ≤ 1 d + 1 ⋅ ∏ j ∉ S i ( 1 − 1 d + 1 ) = r i ⋅ ∏ j ∉ S i ( 1 − r i ) \begin{align} & P(A_i)(d+1) \leq \frac{1}{e} \\ \implies& P(A_i) \leq \frac{1}{d+1} \cdot \frac{1}{e} \leq \frac{1}{d+1} \cdot {\left( 1 - \frac{1}{d+1} \right)}^d \\ &\leq \frac{1}{d+1} \cdot \prod_{j \notin S_i}{\left( 1 - \frac{1}{d+1} \right)} = r_i \cdot \prod_{j \notin S_i} {(1-r_i)} \end{align} ⟹P(Ai)(d+1)≤e1P(Ai)≤d+11⋅e1≤d+11⋅(1−d+11)d≤d+11⋅j∈/Si∏(1−d+11)=ri⋅j∈/Si∏(1−ri)
这样条件就等价变换了 -
然后代入Asymmetric LLL的结果中可以得到:
P ( ∩ i A i ˉ ) ≥ ∏ i ( 1 − r i ) = ( 1 − 1 d + 1 ) n > 0 P(\cap_{i} {\bar {A_i}}) \geq \prod_{i}(1-r_i) = {(1-\frac{1}{d+1})}^n > 0 P(∩iAiˉ)≥i∏(1−ri)=(1−d+11)n>0
结果也与LLL等价了
Asymmetric LLL相较于LLL更加具有普遍性,但从结果上来说也更麻烦了,因为要自己提出 r r r的定义
相关文章:

11 二阶矩方法和Lovasz局部引理
文章目录 11 二阶矩方法和Lovasz局部引理11.1 The Second-Moment Method——二阶矩方法11.1.1 二阶矩方法定理11.1.2 二阶矩方法的应用——随机图阈值 11.2 Lovasz Local Lemma——Lovasz局部引理11.2.1 LLL定理11.2.2 LLL定理证明 11.3 Asymmetric LLL 11 二阶矩方法和Lovasz局…...

低代码赛道拥挤 生态聚合成为破局关键
在云计算和移动互联网的强劲推动下,企业数字化转型的步伐正在加速,对于软件应用开发的需求也呈现出爆发式的增长。这样的背景下,低代码平台凭借其独特的优势迅速崛起并引发了业界的广泛关注。 自2020年以来,低代码领域已成为投资…...
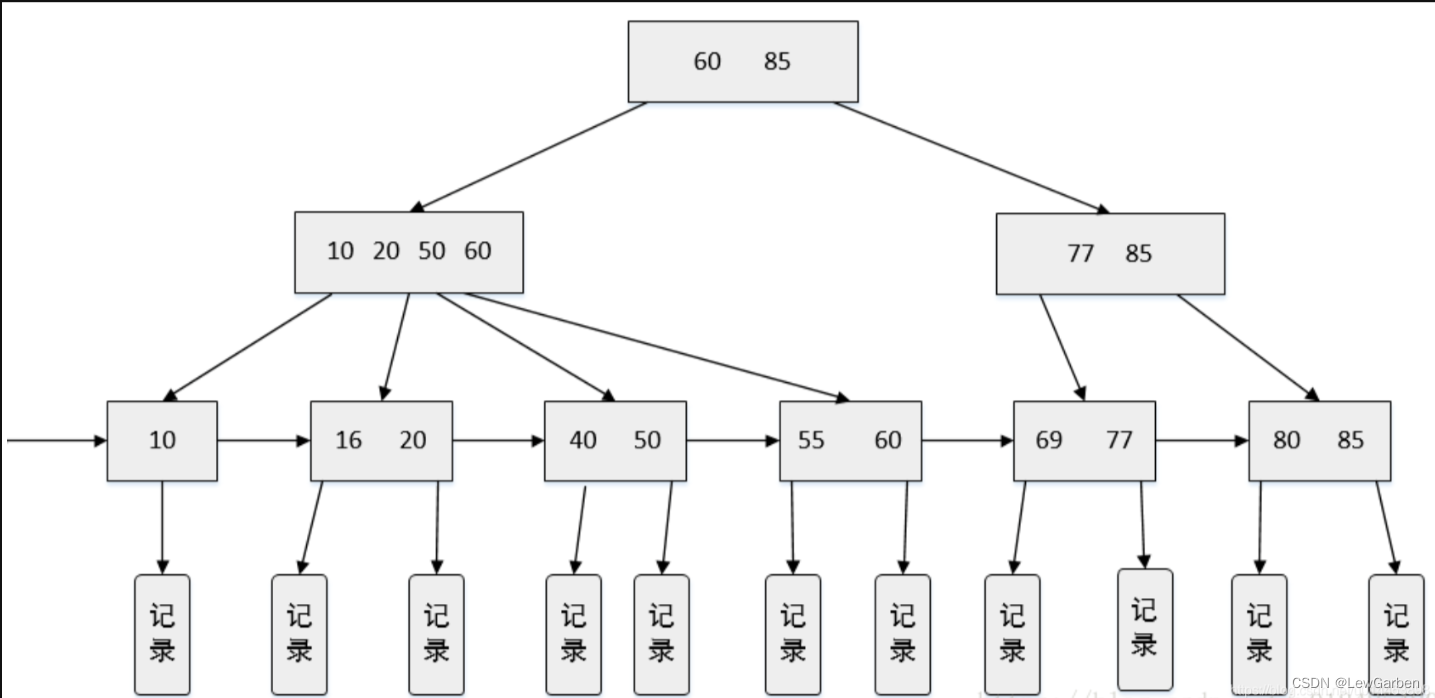
B+树:高效存储与索引的完美结合
目录 引言:一、定义:二、B树和B树三、特点:四、应用场景:总结: 引言: 在计算机科学领域中,数据结构的选择对于高效存储和索引数据至关重要。B树(B tree)作为一种自平衡的…...

左右排版的PDF,如何转换为单栏排版的word?
将左右排版的PDF转换为单行排版的WORD文字版需要进行以下步骤: 1. 使用PDF转换工具将PDF转换为WORD格式。有很多在线或离线的PDF转WORD工具可供选择,例如金鸣表格文字识别、Adobe Acrobat、Smallpdf、Zamzar等。 2. 打开WORD文档后,选择“页…...

D349周赛:注意题目提示里,数据范围隐含的算法复杂度提示
文章目录 6470.既不是最大值也不是最小值完整版为什么两个for循环时间复杂度还是不变的 6465.执行子串操作后的字典序最小字符串思路最开始的写法题意理解的问题 修改版a必须单独拿出来的原因 6449.收集巧克力思路注意提示信息 完整版补充:由数据范围反推算法复杂度…...

iOS -- block one
demo贴上我的github blockOne 块类似于匿名函数或闭包,在许多其他编程语言中也存在类似的概念。 Block 以下是块的一些基本知识: 块的定义:块是由一对花括号 {} 包围的代码片段,可以包含一段可执行的代码。块的定义使用 ^ 符号…...

第十二篇:强化学习SARSA算法
你好,我是郭震(zhenguo) 今天强化学习第二十篇:强化学习SARSA算法 1 历史 SARSA(「State-Action-Reward-State-Action」)算法是一种经典的强化学习算法,用于解决马尔可夫决策过程(MDP࿰…...

电力vr智能巡检模拟实操教学灵活性高成本低
传统电力智能运检服务培训采用交接班期间开展智能带电检测仪器的操作培训,教学时间、场地及材料有限,有了VR技术,将推动电力智能运检服务培训走向高科技、高效率和智能化水平。 深圳华锐视点凭借着对VR实训系统的深入研发和升级,多…...
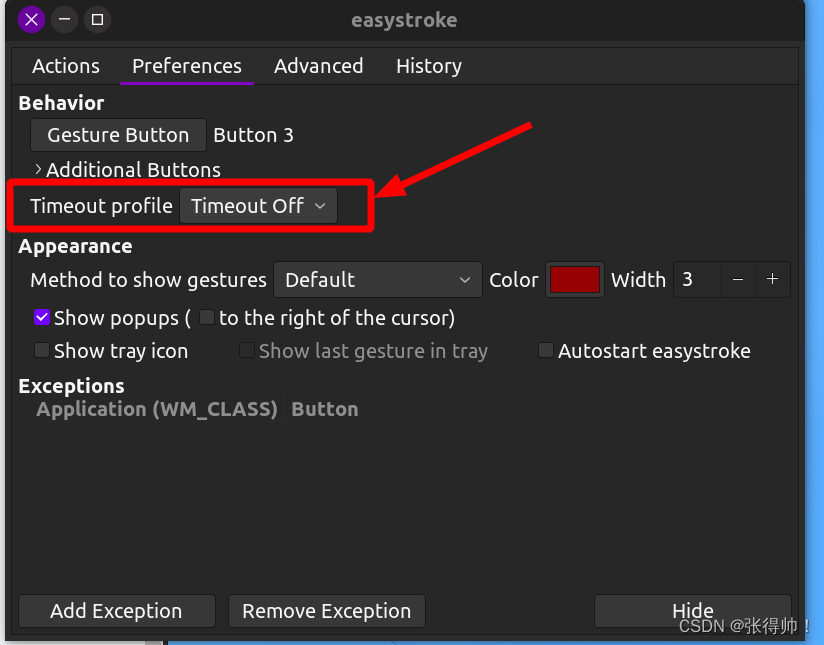
vscode右键点击,松开后自动触发鼠标所在位置的按钮(误触发双击效果)
例如如下,右键展开菜单,松手会自动触发转到声明功能 解决方案: 1、安装easystroke sudo apt-get install easystroke 2、打开easystroke,选择preferences tab 3、点击Gesture Button,在出现的框中右键单击一次 4、点…...

【UE5】分分钟简单使用像素流云服务(Pixel Streaming)
【UE5】分分钟简单使用像素流云服务(Pixel Streaming) 前言 UE5的Pixel Streaming已经封装的很好,简单三步实现简单的服务搭建。 安装插件打包项目运行服务 注:实例平台为Windows 安装插件 编辑→插件→输入查询Pixel Strea…...

2021 年全国硕士研究生入学统一考试管理类专业学位联考逻辑试题
2021 年全国硕士研究生入学统一考试管理类专业学位联考逻辑试题 一. 逻辑推理:第 26~55 小题,每小题 2 分,共 60 分。下列每题给出的 A、B、C、D、E 五个选项中,只有一项是符合试题要求的。 26.哲学是关于世界观、方法论的学问。哲…...

【算法】【算法杂谈】两个排序数组中找第k小的数
目录 前言问题介绍解决方案代码编写java语言版本c语言版本c语言版本 思考感悟写在最后 前言 当前所有算法都使用测试用例运行过,但是不保证100%的测试用例,如果存在问题务必联系批评指正~ 在此感谢左大神让我对算法有了新的感悟认识! 问题介…...

ABAP 新语法--Open SQL(草稿)
1. 常量 1.1 常量赋值 常量字段可以用来为内表中的部分字段赋初始值,字段类型和长度依据输入常量的值决定 SELECTmara~matnr, " 物料号mara~matkl, " 物料组mara~mtart, " 物料类型 AS lkenz, " 删除标识,常量空字符串123 AS fla…...

2023最新常用开发网站汇总
1、在线画图工具 • 在线画图工具ProcessOn:https://www.processon.com/ • 在线画图工具draw.io:https://app.diagrams.net/ • 在线思维导图工具:http://www.mindline.cn/webapp • PlantUML在线编辑器:http://haha98k.com/…...

ELK 日志采集使用
1.安装ELK整体环境 1.1.安装docker环境 Docker 最新版Version 20.10安装_docker最新版本是多少_猿小飞的博客-CSDN博客 1.2.先安装docker compose 安装docker compose_猿小飞的博客-CSDN博客 1.3.使用 Docker Compose 搭建 ELK 环境 1.3.1.编写 docker-compose.yml 脚本启…...

深入剖析RocketMQ源码:消息传递的奥秘
RocketMQ是一款高性能、高可靠性、可扩展性强的分布式消息中间件,能够有效架构企业级分布式应用。由于其广泛应用和优秀表现,越来越多的开发者对RocketMQ的底层实现产生了浓厚的兴趣。本文将深入剖析RocketMQ的消息传递奥秘,帮助大家了解RocketMQ的底层实现原理,进一步掌握…...

Protocol https not supported or disabled in libcurl
原因 curl默认安装完后是只支持http协议而不支持https协议的。 curl -V查看当前curl支持哪些协议: [rootlocalhost /]# curl -V curl 7.19.4 (x86_64-unknown-linux-gnu) libcurl/7.19.4 OpenSSL/1.0.2k zlib/1.2.11 Protocols: tftp ftp telnet dict http fil…...

一步步搭建基于 ts + express + prisma + mongodb + zod 后端服务
环境: windows11、node 18.16.0 、pnpm 1、在合适位置,代开 vscode , 终端执行 mkdir miaooo-backend && cd miaooo-backend && npm init -y 。 创建一个名为一个 miaooo-backend 的项目,并且进入项目 执行 npm 默认初始化。…...
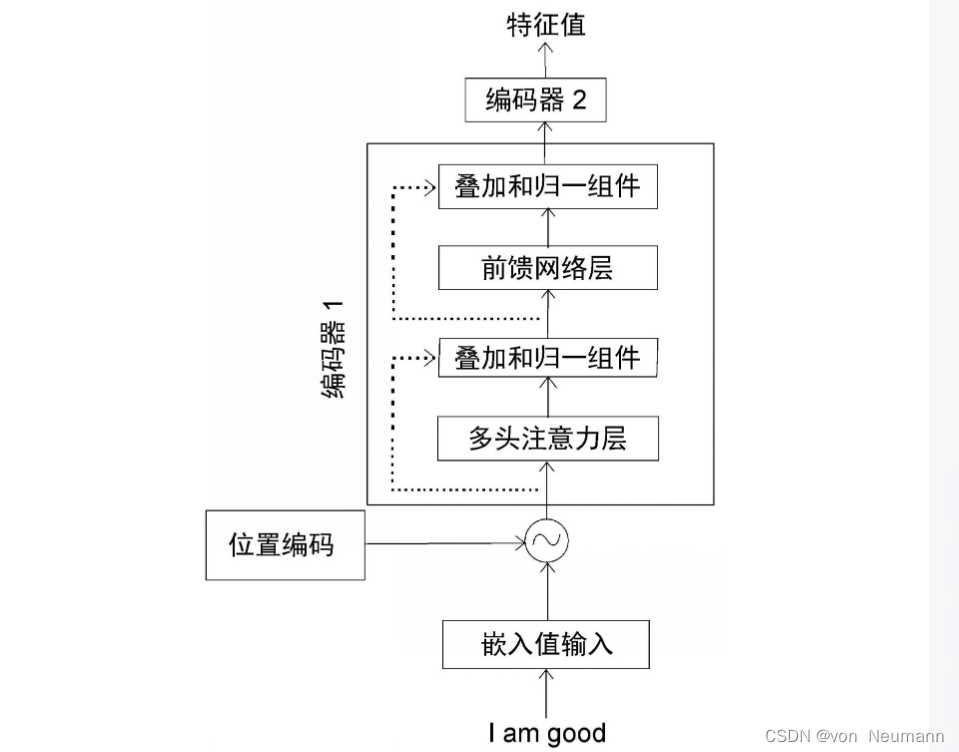
深入理解深度学习——Transformer:编码器(Encoder)部分
分类目录:《深入理解深度学习》总目录 Transformer中的编码器不止一个,而是由一组 N N N个编码器串联而成。一个编码器的输出作为下一个编码器的输入。在下图中有 N N N个编码器,每一个编码器都从下方接收数据,再输出给上方。以此…...

【图像处理】基于收缩系数的粒子群优化和引力搜索算法的多级图像阈值研究【CPSOGSA】(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...
