大学物理(上)-期末知识点结合习题复习(4)——质点运动学-动能定理 力做功 保守力与非保守力 势能 机械能守恒定律 完全弹性碰撞
目录
1.力做功
恒力作用下的功
变力的功
2.动能定理
3.保守力与非保守力
4.势能
引力的功与弹力的功
引力势能与弹性势能
5.保守力做功与势能的关系
6.机械能守恒定律
7.完全弹性碰撞
题1
题目描述
题解
题2
题目描述
题解
1.力做功
物体在力作用下移动
做功
恒力作用下的功
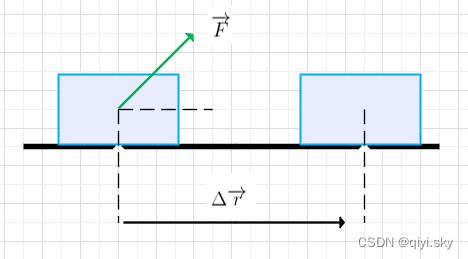
变力的功
运用微积分的思想和方法
变力做功的一般表达式
微分:
积分:
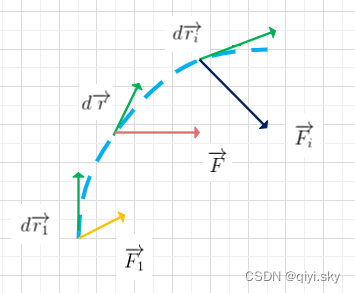
(1)功有正负,由决定。
(2)功是一个过程量,与路径有关。
(3)合力的功,等于各分力的功的代数和。
功的单位:焦耳(J),
2.动能定理
而
所以
动能定理:合外力对质点所做的功,等于质点动能的增量。
注意:(1)功是过程量,动能是状态量;(2)功和动能依赖于惯性系的选取,但对不同惯性系动能定理形式相同。
3.保守力与非保守力
保守力 :做功与路径无关,仅决定于始、末位置的力。(万有引力、重力、弹性力和静电场力)
非保守力:所做的功与路径有关的力。(例如摩擦力)
4.势能
势能:因相对位置而具有的做功本领称为势能或位能(因有速度而具有的做功本领称为动能)。势能与质点的位置有关。
引力的功与弹力的功
引力的功:
弹力的功:
引力势能与弹性势能
引力势能:
弹性势能:
注意: (1)势能是状态的函数
(2)势能具有相对性,势能大小与势能零点的选取有关。
(3)势能是属于系统的。
(4)势能差与势能零点选取无关。
5.保守力做功与势能的关系
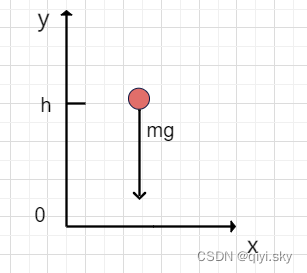
重力势能的计算:
保守力做功:
保守力做功,势能减少。
二者的关系:保守力做功等于等于势能的减少。
6.机械能守恒定律
由功能原理:
为外力,
为非保守内力。
如果:
则:
或:常量
机械能守恒定律
如果系统内只有保守内力做功,其他内力和一切外力都不做功,则系统内各物体的动能和势能可以相互转换,但总机械能保持不变。
7.完全弹性碰撞
如果在碰撞后,两物体的动能完全没有损失,我们就称这种碰撞为弹性碰撞(或完全弹性碰撞)。
在一般情况下,两物体碰撞时,总要损失一大部分动能(转变为其他形式的能量,例如放出热量等),这种碰撞就称为非弹性碰撞。
如果两物体在碰撞后,以同一速度运动,并不分开,这种就称为完全非弹性碰撞。
一般碰撞时,如果,即内力远远大于外力,则可以近似地看为完全弹性碰撞。
在完全弹性碰撞的情况中:动量守恒,机械能守恒。
其余碰撞都为:动量守恒,但机械能不守恒。
题1
题目描述
对质点系有以下几种说法:
(1)质点系总动量的改变与内力无关;
(2)质点系总动能的改变与内力无关;
(3)质点系机械能的改变与保守内力无关。
下列对上述说法判断正确的是()
(A)只有(1)是正确的
(B)(1)、(2)是正确的
(C)(1)、(3)是正确的
(D)(2)、(3)是正确的
题解
(1)是正确的,假设在以下场景
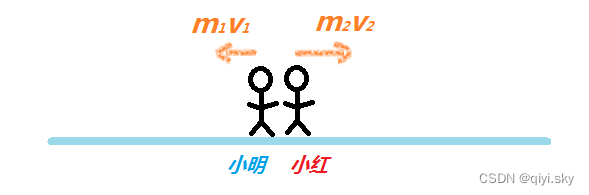
小明和小红在光滑的冰面上,一开始两人都静止;后面两个人相互推了对方一下,那么他们两个就开始相互向后撤离;小明由于体重比较大,所以向后撤离的速度会稍微慢一点,小红则是体重比较小,向后撤离的速度会快一点;但是他们二者之间的乘积大小都是一样的,保证了整个系统总的动量跟之前是相同的。
而他们之间只受到了对方的推力,这种推力就是系统中的内力,这个内力不会改变他们以他们两个系统的总动量。故而(1)正确。
(2)是错误的,还是以之前的场景来看:
最开始以他们两个为系统的情况下,小明和小红都是静止的,所以他们二者的动能都是为零的;(由动能的定义)
后面推开了之后,两个人都有了速度,虽然二者的速度方向是相反的,但算的是动能,矢量速度平方之后也变成了一个标量,也就是说没有正负号之分了。
所以总动能肯定是增加的,故而(2)错误。
(3)也是正确的,机械能分为两个部分:动能和势能;而势能也有两部分:重力势能和弹性势能。
这里的重力势能和弹性势能对应的力是重力、万有引力和弹性力,他们都是一种弹性力。
我们可以把这样的一句话记住:只有保守内力做功的情况下,系统的机械能守恒。
综上,最终答案应选择C。
题2
题目描述
对功的概念有以下几种说法:
(1)保守力做正功时,系统内相应的势能增加;
(2)质点运动经一闭合路径,保守力对质点做的功为零;
(3)作用力和反作用力大小相等,方向相反,所以二者所做功的代数和必为零 。
下列对上述说法判断正确的是()
(A)(1)、(2)是正确的
(B)(2)、(3)是正确的
(C)只有(2)是正确的
(D)只有(3)是正确的
题解
(1)是错误的,做题的时候脑子里最好要能够浮现出相应的情景;随便想象一个场景,重力(保守内力)做正功的情况,即物体下落:

很显然势能应该是减少的。故而(1)错误。
(2)是正确的,其中描述的正是保守力的一个特点,事实上,就是根据这样一个特点才定义出一个保守力的概念。故而是正确的。
(3)也是错误的,前半句是正确的,反作用力大小相等,方向相反,但是二者所做功的代数和不一定为零 。
我们举下面这个例子来证明一下:

一个木块放在一辆小车上,突然给这个木块施加一个力,使其拥有一个初速度。木块和小车就会开始运动,这时就会有一队作用力和反作用力:.计算他们所做功的代数和,已知他们的位移分别为
.
明显会更大一点,所以计算出来的功的大小较大,且为负数;而
较小,计算出来的功的大小较小,为正数,故而二者的代数和并不为零。
即
故而(3)错误。
题3
题目描述
有两个倾角不同、高度相同、质量一样的斜面放在光滑的水平面上,斜面是光滑的,有两个一样的物块分别从这两个斜面的顶点由静止开始滑下,则()
(A)物块到达斜面底端时的动量相等
(B)物块到达斜面底端时动能相等
(C)物块和斜面(以及地球) 组成的系统,机械能不守恒
(D)物块和斜面组成的系统水平方向上动量守恒
题解
画出情景:
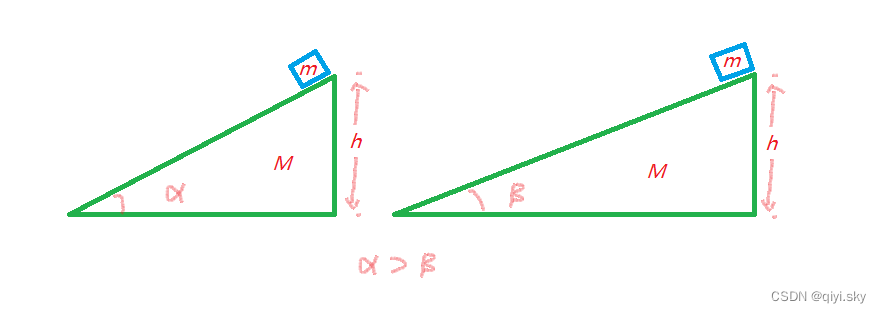
先看A选项,到达底端动量相等,由动量的定义:,动量和速度都为矢量,需要考虑方向性;已知两个斜面的倾角是不一样的,所以很显然到达底端时所拥有的速度在方向上是一定不一样的,动量也就不相等。故而A选项错误。
B选项,物块到达底端的动能相等,这个选项的情况,因为斜面放在光滑的水平面上,在小物块往下滑的过程中,斜面也在向右运动;而两个斜面拥有的速度一定是不相同的,怎么得出这个结论的呢?
我们利用反证法:
假设两个斜面速度相同,由于小物块和斜面之间只有相互之间的支持力,即只有内力,而内力不改变整个系统的动量,那么就可以判断小物块在向左下方运动时的水平方向上的分速度是相同的,即水平方向上,动量要守恒。
小物块水平方向上的分速度相同的情况下,由于倾角不同,那么小物块最终的速度自然就是v左大于v右,也就是小物块的动能是不相同的。
总的看下来,情况就是:两个小物块的动能不同,而两个斜面的动能却是相同的。
这在同样的重力做功,同样的能量转换的情况下,是矛盾的,所以我们才说两个斜面的速度一定是不相同的。
那么知道了斜面的速度是不相同了之后,因为系统能量是守恒的,小物块和斜面能量之和应该是一个定值,所以两个小物块的动能也是不相同的。故而B选项错误。
再看C选项,物块和斜面(以及地球) 组成的系统机械能守不守恒,如果只有保守内力做功,那么机械能一定是守恒的;但是系统中还有支持力、弹力和压力,这些力是否做功呢?
看到情景中就可以判断出来,这些支持力、弹力和压力,都是与运动路径互相垂直的,也就是不做功,所以整个系统机械能一定是守恒的。故而C选项错误。
最后看D选项,是说物块和斜面组成的系统水平方向上动量守恒,这一点刚刚在前面我们就提到过了,在水平方向上没有任何外力做功。
综上,这道题应选择D选项。
end
相关文章:
大学物理(上)-期末知识点结合习题复习(4)——质点运动学-动能定理 力做功 保守力与非保守力 势能 机械能守恒定律 完全弹性碰撞
目录 1.力做功 恒力作用下的功 变力的功 2.动能定理 3.保守力与非保守力 4.势能 引力的功与弹力的功 引力势能与弹性势能 5.保守力做功与势能的关系 6.机械能守恒定律 7.完全弹性碰撞 题1 题目描述 题解 题2 题目描述 题解 1.力做功 物体在力作用下移动做功…...
这两个小众的资源搜索工具其实很好用
01 小不点搜索是一个中国网络技术公司开发的网盘搜索引擎,该网站通过与多个主流网盘进行整合,为用户提供一种快速查找和下载文件的方式。小不点搜索因其高效性、便利性和实用性受到了广大用户的喜爱。 在技术实现上,小不点搜索拥有先进的搜…...
— 单例模式1)
Java设计模式(六)— 单例模式1
系列文章目录 单例模式介绍 单例模式之静态常量饿汉式 单例模式之静态代码饿汉式 单例模式之线程不安全懒汉式 文章目录 系列文章目录前言一、单例设计模式介绍二、单例设计模式八种方式三、单例—静态常量饿汉式1.静态常量饿汉式介绍2.静态常量饿汉式案例3.静态常量饿汉式优缺…...
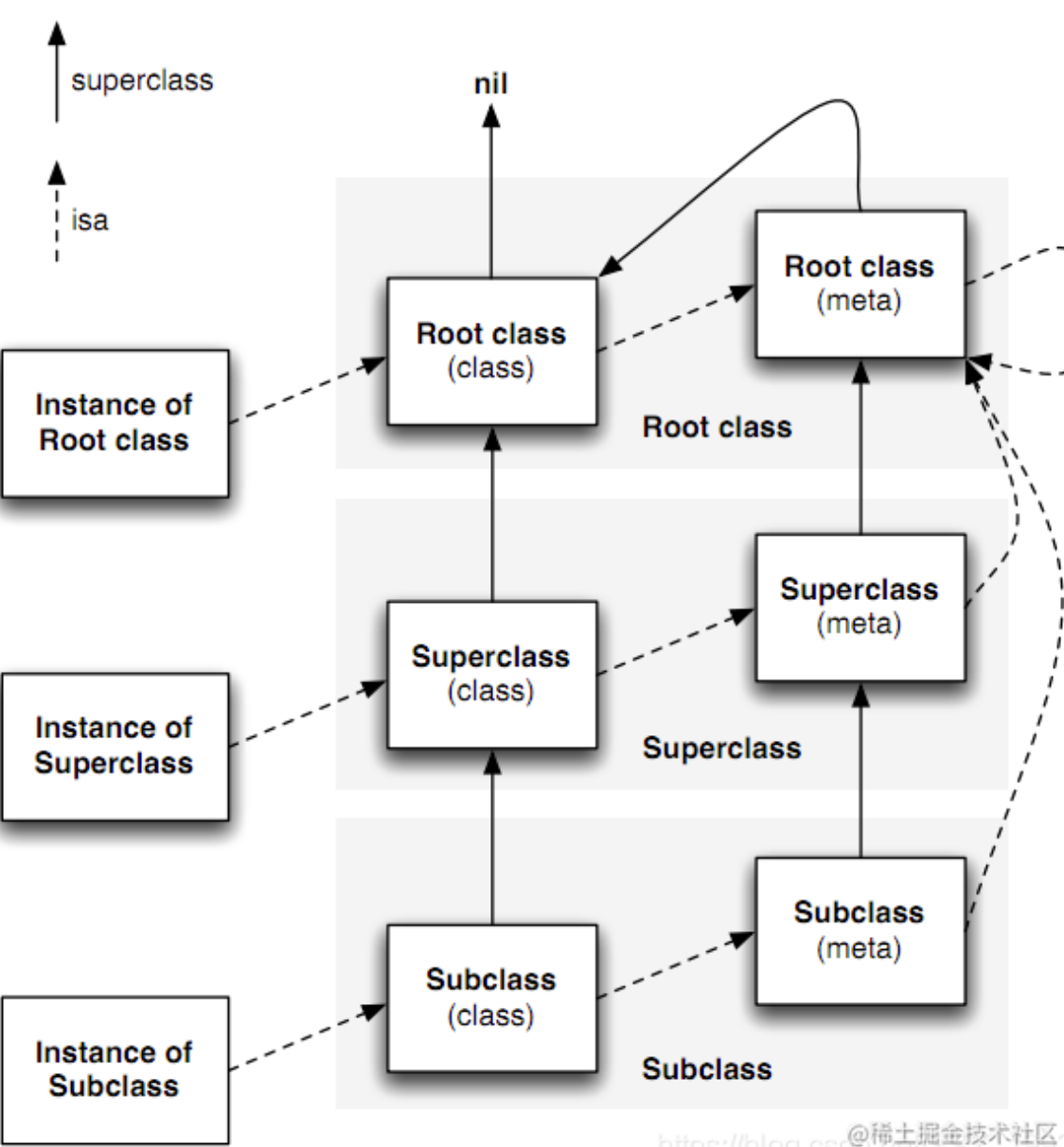
iOS -- isa指针
isa指针:isa指针是一个指向对象所属类或元类的指针。它决定了对象可以调用的方法和属性。isa指针在对象的结构中存在,并且在运行时会被自动设置。isa 指针,表示这个对象是一个什么类。而 Class 类型, 也就是 struct objc_class * …...

【SA8295P 源码分析】14 - Passthrough配置文件 /mnt/vm/images/linux-la.config 内容分析
系列文章汇总见:《【SA8295P 源码分析】00 - 系列文章链接汇总》 本文链接:《【SA8295P 源码分析】14 - Passthrough配置文件 /mnt/vm/images/linux-la.config 内容分析》 透传配置文件位于:qnx.git\apps\qnx_ap\target\hypervisor\gvm\ivi\la\linux-la.config 它是在QNX Ho…...
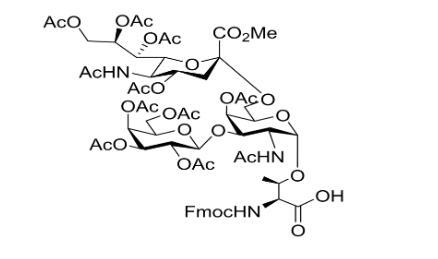
新型糖基化氨基酸:Fmoc-Thr((Ac4Galβ1-3)Me,Ac4Neu5Acα2-6AcGalNAcα)-OH,化学CAS号174783-92-7
●英文名:Fmoc-Thr((Ac4Galβ1-3)Me,Ac4Neu5Acα2-6AcGalNAcα)-OH ●外观以及性质: Fmoc-Thr((Ac4Galβ1-3)Me,Ac4Neu5Acα2-6AcGalNAcα)-OH中通过对蛋白进行复杂蛋白糖基化修饰,细胞产生了极大丰度的蛋白质类型;通过对各类糖基…...

网络安全(黑客)怎么自学?
最近看到很多问题,都是小白想要转行网络安全行业咨询学习路线和学习资料的,作为一个培训机构,学习路线和免费学习资料肯定是很多的。机构里面的不是顶级的黑阔大佬就是正在学习的同学,也用不上这些内容,每天都在某云盘…...

Vue学习 之 MacOS 安装 webpack
Vue学习 之 MacOS 安装 webpack webpack 简介 Webpack 是一个非常流行的前端构建工具,它可以将多个模块(包括CSS、JavaScript、图片等)打包成一个或多个静态资源文件(bundle),以便用于部署到生产环境。We…...

媒介易教你海外品牌推广:如何选择适合的新闻通稿发布平台?
在进行海外品牌推广时,选择合适的海外新闻通稿发布第三方平台是提高品牌曝光度和影响力的重要一环。这些平台可以帮助企业将新闻内容传播到全球范围内的媒体和受众,为品牌推广提供更广阔的机会。然而,选择合适的发布平台并不容易,…...

网络安全的学习路线是怎么样的?
最近看到网上有很多人在问诸如:“怎样成为网络安全工程师”等相关问题,这可能与近几年网络安全事件频发,国家对于互联网信息安全和互联网舆情的重视程度不断提升有关,网络信息安全工程师随之成为炙手可热的职业。关于职业前景的详…...

QT学习07:五种按钮控件
文章首发于我的个人博客:欢迎大佬们来逛逛 文章目录 抽象类:QAbstractButtonQPushButtonQToolButtonQCommandLinkButtonQRadioButtonQCheckBoxQButtonGroup 抽象类:QAbstractButton 是所有按钮类的祖先。 QAbstractButton的信号:…...

chatgpt赋能python:Python如何截图运行结果
Python如何截图运行结果 介绍 Python是一种高级编程语言,非常流行。它具有许多有用的功能和库,使其成为许多开发人员的首选编程语言之一。但是,当您运行Python程序并需要与他人共享结果时,您可能需要截图运行结果。在本文中&…...
)
Baumer工业相机堡盟工业相机如何通过BGAPISDK使用JPEG图像压缩功能(C#)
Baumer工业相机堡盟工业相机如何通过BGAPISDK使用JPEG图像压缩功能(C#) Baumer工业相机Baumer工业相机BGAPISDK和JPEG图像压缩功能的技术背景Baumer工业相机通过BGAPISDK使用JPEG图像压缩功能1.引用合适的类文件2.使用BGAPISDK设置堡盟相机JPEG图像压缩模…...

RT-Thread FAL组件
目录 1、FAL介绍2、使用FAL2.1 下载FAL软件包2.2 FAL移植2.2.1 定义flash设备2.2.2 定义flash设备表&分区表2.2.3 加入到mdk工程3、MSH测试1、FAL介绍 FAL(Flash Abstraction Layer) Flash抽象层,是对Flash及基于Flash的分区进行管理、操作的抽象层,对上层统一了Flash及分…...
【git切换分支/tag】git stash保存暂不提交的更改
目录 问题git stash使用方法git stash pop 还原修改 git stash使用、修改指定tag的代码 其他git指令 问题 情景:分支1上开发新功能,临时切换到其他分支或tag上修改bug。 1、直接切换:如果没有冲突,分支1的修改会带到要切换的分支…...

【爬虫】4.5 实践项目——爬取当当网站图书数据
目录 1. 网站图书数据分析 2. 网站图书数据提取 3. 网站图书数据爬取 (1)创建 MySQL 数据库 (2)创建 scrapy 项目 (3)编写 items.py 中的数据项目类 (4)编写 pipelines_1.py …...

Socket 编程:基础概念辨析
文章目录 参考Socket APIBSD UNIX 操作系统BSD UNIX 与 Socket API Socket套接字套接字地址套接字 VS 套接字地址套接字的表示方法 TCP 套接字与 UDP 套接字TCP 套接字监听套接字连接套接字 UDP套接字 TCP 服务器端与 TCP 客户端通信的基本流程服务器端客户端 参考 项目描述刘…...

git lfs下载指定文件git lfs pull --include=“*.bin“
git lfs pull --include"*.bin"...

JavaScript 数组 函数
目录 1.数组的概念 2.创建数组 2.1 数组创建的方式 2.2利用new 创建数组 2.3 利用数组字面量创建数组 2.4 数据元素的类型 3.获取数组当元素 3.1数组元素的索引 4.遍历数组 4.1数组的长度 5.数组中新增元素 5.1通过修改length 长度新增数组元素 5.2通过修改数组索引…...

【哈佛积极心理学笔记】第7讲 逆境还是机遇
第7讲 逆境还是机遇 How can we raise base level? One of the things is coping, putting ourselves on the line. How to become an optimist. Optimism as an interpretation style, not as a Pollyannaish feel good kind of approach. Three approaches: First is to t…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...
