算法模板(5):数学(1):数学知识(1)
数论
整数的整除性
- [x]表示不超过x的最大整数,叫做取整函数或高斯函数。
- 设整数a,b不同时为零,则存在一对整数m,n,使得 ( a , b ) = a m + b n (a, b) = am + bn (a,b)=am+bn。注:a和b的最大公因数会写成 (a, b) 的形式,最小公倍数会写成 [a, b] 的形式。
- 若 a ∣ b c a\ |\ bc a ∣ bc,且 ( a , b ) = 1 (a, b) = 1 (a,b)=1,则 a ∣ c a\ |\ c a ∣ c。
- 设p为素数,若 p ∣ a b p\ |\ ab p ∣ ab,则 p ∣ a p\ |\ a p ∣ a,或 p ∣ b p\ |\ b p ∣ b。推论:设p为素数,若 p ∣ a 1 a 2 . . . a k p\ |\ a_1a_2...a_k p ∣ a1a2...ak,则存在 a i ( 1 ≤ i ≤ k ) a_i(1\le i \le k) ai(1≤i≤k),使得 p ∣ a i p\ |\ a_i p ∣ ai。
- ( a , b ) [ a , b ] = ∣ a b ∣ (a, b)[a, b] = |ab| (a,b)[a,b]=∣ab∣.
- 求多个整数的最大公因数,可以这样转化:(a, b, c) = ((a, b), c)。求多个整数的最大公倍数,可以转化为:[a, b, c] = [[a, b], c]。
- 算术基本定理:任何大一1的整数可以分解成素因数乘积的形式,并且,如果不计分解式中素因数的次序,这种分解式是惟一的。
- 一般地,对给定的两个大于1的整数a, b,找出它们所有的互异素因数,然后将a, b表示成这些素因数的幂的乘积,如果其中一个素因数在a或b中不出现,就将这个素因数的幂指数写作0,那么(a, b)可以表示成这些素因数的幂的乘积,每个素因数的幂指数为其在a与b中的幂指数的最小者,而[a, b]也可以表示成这些素因数幂的乘积,每个素因数的幂指数为其在a与b的幂指数的最大者.
同余
- a ≡ b ( m o d n ) ⇔ n ∣ a − b a\equiv b(mod\ n)\Leftrightarrow n|a-b a≡b(mod n)⇔n∣a−b.
- 若 a ≡ b ( m o d n ) a\equiv b(mod\ n) a≡b(mod n),且 c ≡ d ( m o d n ) c\equiv d(mod\ n) c≡d(mod n),则
- a + c ≡ b + d ( m o d n ) a+c\equiv b+d(mod\ n) a+c≡b+d(mod n);
- a c ≡ b d ( m o d n ) ac\equiv bd(mod\ n) ac≡bd(mod n)
- k a ≡ k b ( m o d n ) ka\equiv kb(mod\ n) ka≡kb(mod n),k为任意整数
- a m ≡ b m ( m o d n ) a^m \equiv b^m(mod\ n) am≡bm(mod n),m为正整数
- 若 a b ≡ a c ( m o d n ) ab\equiv ac(mod\ n) ab≡ac(mod n),且 ( a , n ) = 1 (a, n) = 1 (a,n)=1,则 b ≡ c ( m o d n ) b\equiv c(mod\ n) b≡c(mod n).
- 我们把所有与整数a模n同余的整数构成的集合叫做模n的一个剩余类,记作[a],并把a叫做剩余类[a]的一个代表元。
- a ≡ b ( m o d n ) ⇔ [ a ] = [ b ] . a\equiv b(mod\ n) \Leftrightarrow [a] = [b]. a≡b(mod n)⇔[a]=[b].
- 剩余类加法: [ a ] + [ b ] = [ a + b ] [a] + [b]=[a+b] [a]+[b]=[a+b]。剩余类乘法: [ a ] [ b ] = [ a b ] [a][b]=[ab] [a][b]=[ab]。
- [0]叫剩余类环的零元,[1]叫剩余类环的单位元。若 [ a ] + [ b ] = [ b ] + [ a ] = [ 0 ] [a]+[b]=[b]+[a]=[0] [a]+[b]=[b]+[a]=[0],则称[b]为[a]的负元。若 [ a ] [ b ] = [ b ] [ a ] = [ 1 ] [a][b]=[b][a]=[1] [a][b]=[b][a]=[1],则称[b]为[a]的逆元。
- 非零元[a]有逆元的充要条件是 ( a , n ) = 1 (a, n)=1 (a,n)=1。n就是剩余类定义里面的那个n。
- 在模n的剩余类环中,若[a]存在逆元,则它的逆元仅有一个。
- 无零因子:任意两个非零整数的乘积不等于0。但是,剩余类乘法中并不都满足这个条件。比如模6的剩余类乘法, [ 2 ] [ 3 ] = 0 [2][3]=0 [2][3]=0。但是模5的剩余类环无零因子。
- 设m为素数,a为任意整数,且 ( a , m ) = 1 (a, m)=1 (a,m)=1,则 a m − 1 ≡ 1 ( m o d m ) a^{m-1}\equiv 1(mod\ m) am−1≡1(mod m).
- 欧拉定理:设 m 为正整数,a 为任意整数,且 ( a , m ) = 1 (a, m) = 1 (a,m)=1,则: a ϕ ( m ) ≡ 1 ( m o d n ) a^{\phi(m)}\equiv 1(mod\ n) aϕ(m)≡1(mod n),其中 ϕ ( m ) \phi(m) ϕ(m)表示1,2,3,…,m 中与m互素的正整数的个数。若在算数基本定理中, N = p 1 a 1 ∗ p 2 a 2 ∗ … ∗ p m a m N=p_1^{a_1}*p_2^{a_2}*…*p_m^{a_m} N=p1a1∗p2a2∗…∗pmam,则: φ ( N ) = N ∗ p 1 − 1 p 1 ∗ p 2 − 1 p 2 ∗ … ∗ p m − 1 p m \varphi(N)=N*\frac{p_1 - 1}{p_1}∗\frac{p_2−1}{p_2}∗…∗\frac{p_m−1}{p_m} φ(N)=N∗p1p1−1∗p2p2−1∗…∗pmpm−1。不过要指出的是, φ ( 1 ) = 1 \varphi(1)=1 φ(1)=1。
- 一次同余方程 a x ≡ b ( m o d n ) ax\equiv b(mod\ n) ax≡b(mod n)有解,则 ( a , n ) ∣ b (a, n)|b (a,n)∣b。反过来,当 ( a , n ) ∣ b (a, n)|b (a,n)∣b,一次同余方程 a x ≡ b ( m o d n ) ax\equiv b(mod\ n) ax≡b(mod n)恰有(a, n)个解。
- b a % p = b ∗ a − 1 % p = b ∗ a p − 2 % p \frac{b}{a} \ \% \ p = b * a^{-1} \ \% \ p = b * a^{p-2} \ \% \ p ab % p=b∗a−1 % p=b∗ap−2 % p
一次不定方程
- 二元一次不定方程 a x + b y = c ax+by=c ax+by=c有解,等价于 ( a , b ) ∣ c (a, b)|c (a,b)∣c。
- 设 ( a , b ) = 1 (a, b)=1 (a,b)=1,则不定方程ax+by=c的整数通解为 { x = x 0 + b t y = y 0 − a t \begin{cases}x=x_0+bt\\y=y_0-at\end{cases} {x=x0+bty=y0−at其中t为任意整数, x = x 0 , y = y 0 x=x_0,y=y_0 x=x0,y=y0为不定方程 a x + b y = c ax+by=c ax+by=c的一个特解。
- 三元一次不定方程 a x + b y + c z = d ax+by+cz=d ax+by+cz=d有整数解的充要条件是 ( a , b , c ) ∣ d (a,b,c)|d (a,b,c)∣d
原根与指数
原根
- 设(a,m) = 1,则
(i)存在正整数n, 1 ≤ r < m 1≤ r< m 1≤r<m,使 a n = 1 a^n= 1 an=1(mod m);
(ii)设n为(i)中最小的正整数,则对整数k和l,同余式 a k = a l ( m o d m ) a^k=a^l(mod\ m) ak=al(mod m) 成立的充分必要条件是 k ≡ l ( m o d n ) k\equiv l(mod\ n) k≡l(mod n).特别地, a k = 1 ( m o d m ) a^k= 1(mod\ m) ak=1(mod m)成立的充分必要条件为n|k. - 对与m互素的整数a,满足 a n = 1 ( m o d m ) a^n= 1(mod\ m) an=1(mod m)的最小正整数n,称为a模m的阶.
组合数学
组合数
- 一个组合数是否为奇数: C ( n , k ) C(n,k) C(n,k)为奇数时, n & k = k n\&k=k n&k=k 。
- 令 a n = ∑ x = 0 N C N x ∗ 2 x a_n =\sum_{x=0}^NC_N^x*2^x an=∑x=0NCNx∗2x: a 0 = 1 a_0 =1 a0=1, a n = 3 ∗ a n − 1 a_n = 3*a_{n-1} an=3∗an−1。
求和公式
1.平方和公式
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-SemLiPww-1686468029027)(null)]
2.立方和公式
∑ i = 1 n i 3 = 1 3 + 2 3 + . . . + n 3 = n 2 ( n + 1 ) 2 4 = [ n ( n + 1 ) 2 ] 2 \sum\limits_{i = 1}^{n} i^3= 1^3 + 2 ^ 3 + ... + n^3 = \frac{n^2(n+1)^2}{4}=[\frac{n(n+1)}{2}]^2 i=1∑ni3=13+23+...+n3=4n2(n+1)2=[2n(n+1)]2
微积分
积分表
- 积分表1:
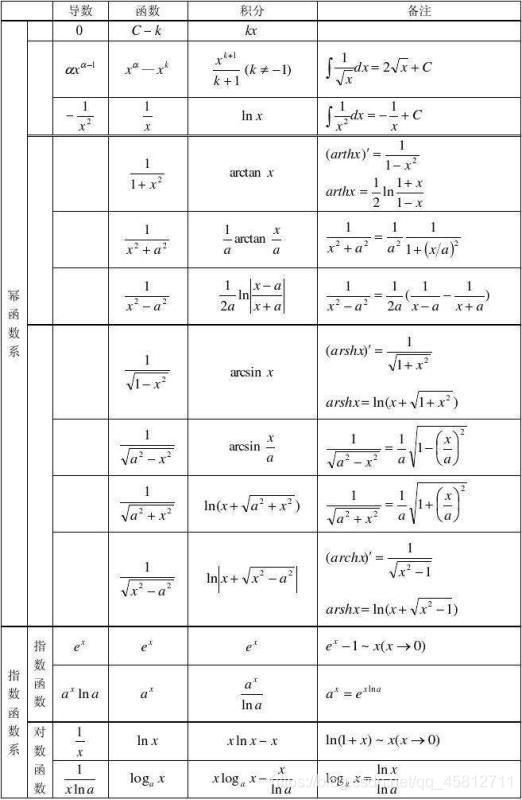
- 积分表2:

- 积分表3:
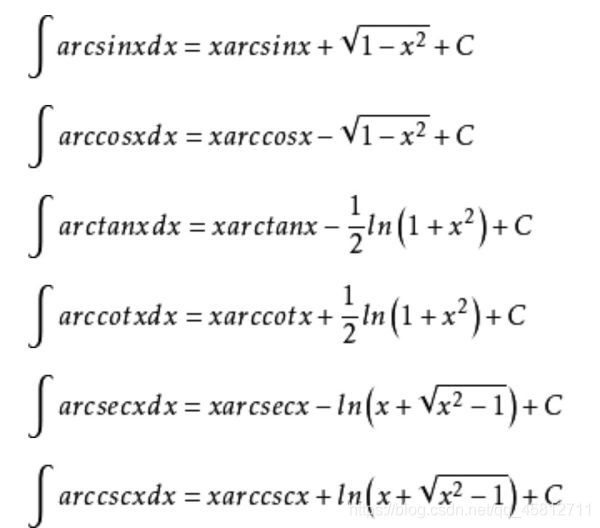
π \pi π 的值
- 不用记住准确值,一行代码就可以了呀。把这个放在main函数外面也是没问题的。
const double PI = acos(-1);
其他
- 在数学中,以Kenneth E. Iverson命名的“艾佛森括号”,是一种用方括号记号,如果方括号内的条件满足则为1,不满足则为0。
- 格雷码规则:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-NC5Ypxxs-1686468028452)(file:///D:\1398687709\1398687709\Image\C2C\3144C8683FBA94C26F58702AA73A398E.png)]
相关文章:
算法模板(5):数学(1):数学知识(1)
数论 整数的整除性 [x]表示不超过x的最大整数,叫做取整函数或高斯函数。设整数a,b不同时为零,则存在一对整数m,n,使得 ( a , b ) a m b n (a, b) am bn (a,b)ambn。注:a和b的最大公因数会写成 (a, b)…...
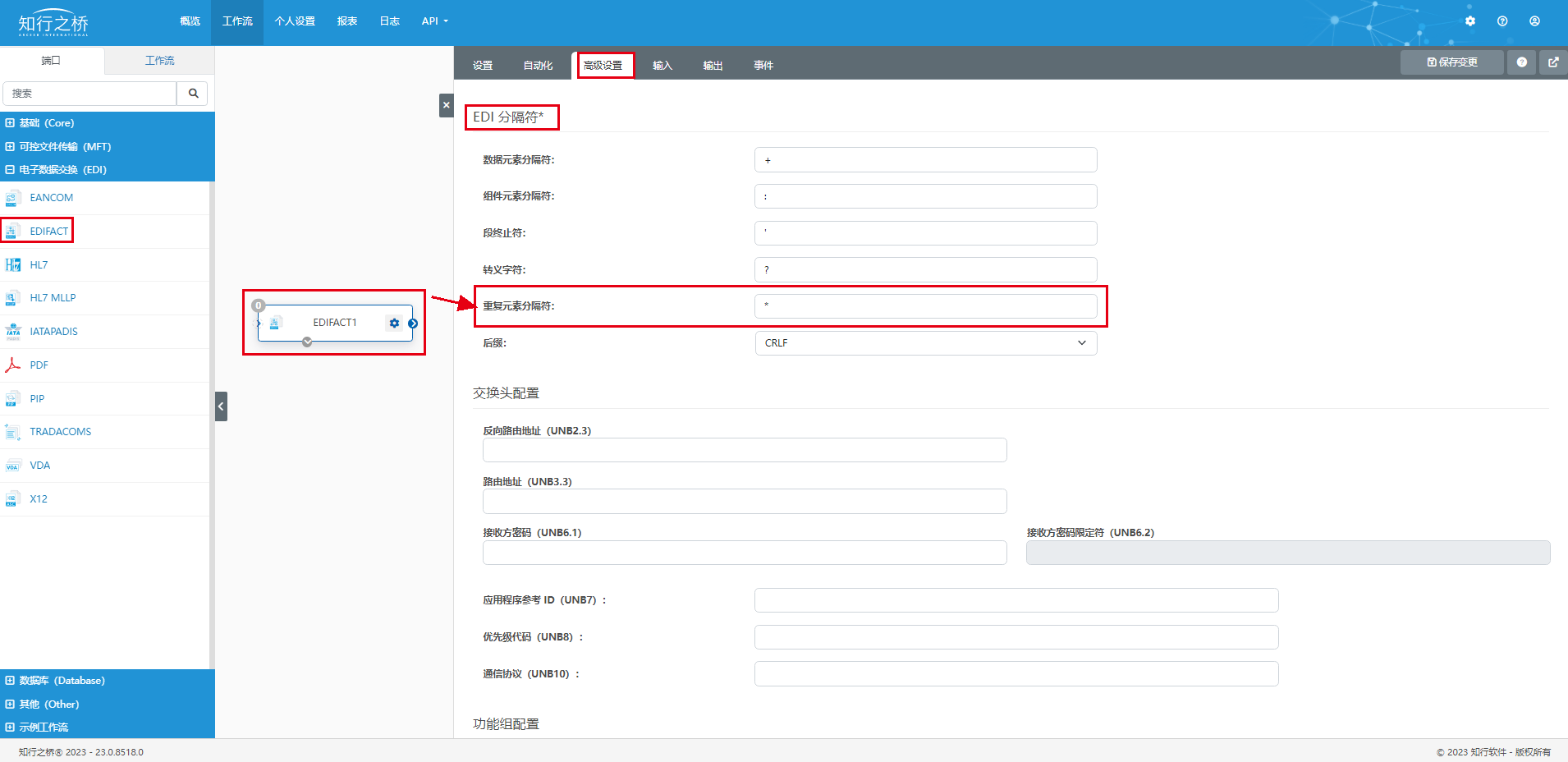
电子行业 K 公司对接 Nexperia EDI 项目案例
项目背景 Nexperia 是一家全球领先的半导体制造商,专注于提供高性能、高可靠性和创新性的半导体解决方案。公司成立于2017年,是前飞思卡尔半导体业务的一部分,并在全球范围内拥有多个设计、研发和生产基地。 Nexperia 使用 EDI(…...

chatgpt赋能python:Python如何将英文转化为中文的最佳方法
Python如何将英文转化为中文的最佳方法 介绍 在现代全球化社会中,国与国之间的交流越来越频繁,相应的语言翻译工具的需求也愈发迫切。Python是一种易于学习、快速上手的编程语言,适合初学者和经验丰富的程序员使用,在语言翻译方…...
知道这些英文文档翻译的方式吗
在工作中,大家有没有遇到领导交给你一份外语的文档,要你去观看和理解,但是我们看不太懂或者没啥时间去一点点翻译怎么办呢?我们就需要有工具来将文档翻译,它是一项非常实用和便捷的功能,它可以将文档中的文…...
供应链安全
供应链安全 目录 文章目录 供应链安全目录本节实战可信任软件供应链概述构建镜像Dockerfile文件优化镜像漏洞扫描工具:Trivy检查YAML文件安全配置:kubesec准入控制器: Admission Webhook准入控制器: ImagePolicyWebhook关于我最后…...

华硕天选4原装Windows11系统带ASUSRECOVERY恢复工厂模式安装
华硕工厂恢复系统 ,安装结束后带隐藏分区以及机器所有驱动软件,奥创Myasus Recovery 文件地址https://pan.baidu.com/s/1Pq09oDzmFI6hXVdf8Vqjqw?pwd3fs8 提取码:3fs8 文件格式:5个底包(HDI KIT COM MCAFEE EDN) 1个引导工具TLK 支持ASUSRECOVERY型…...
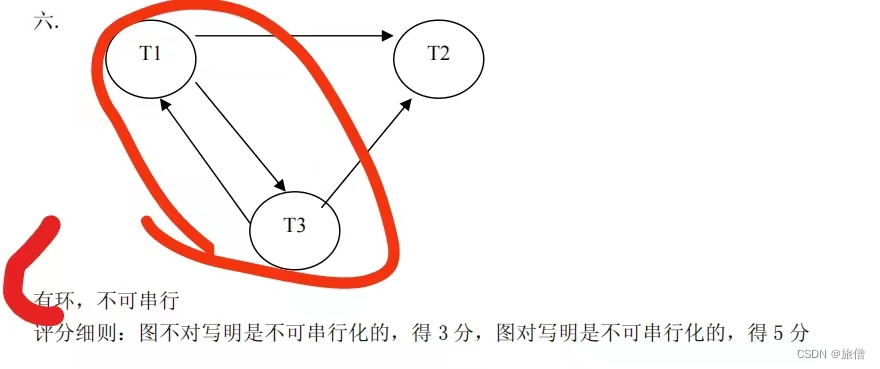
数据库期末复习(8)并发控制
笔记 数据库DBMS并发控制(1)_旅僧的博客-CSDN博客 数据库 并发控制(2)死锁和意向锁_旅僧的博客-CSDN博客 同一个对象不能既有slock又有xlock; 冲突可串行化和锁 怎么判断是否可以进行冲突可串行化:简便的方法是优先图 只有不同对象和同一对象都是读才不能发生非串行化调…...
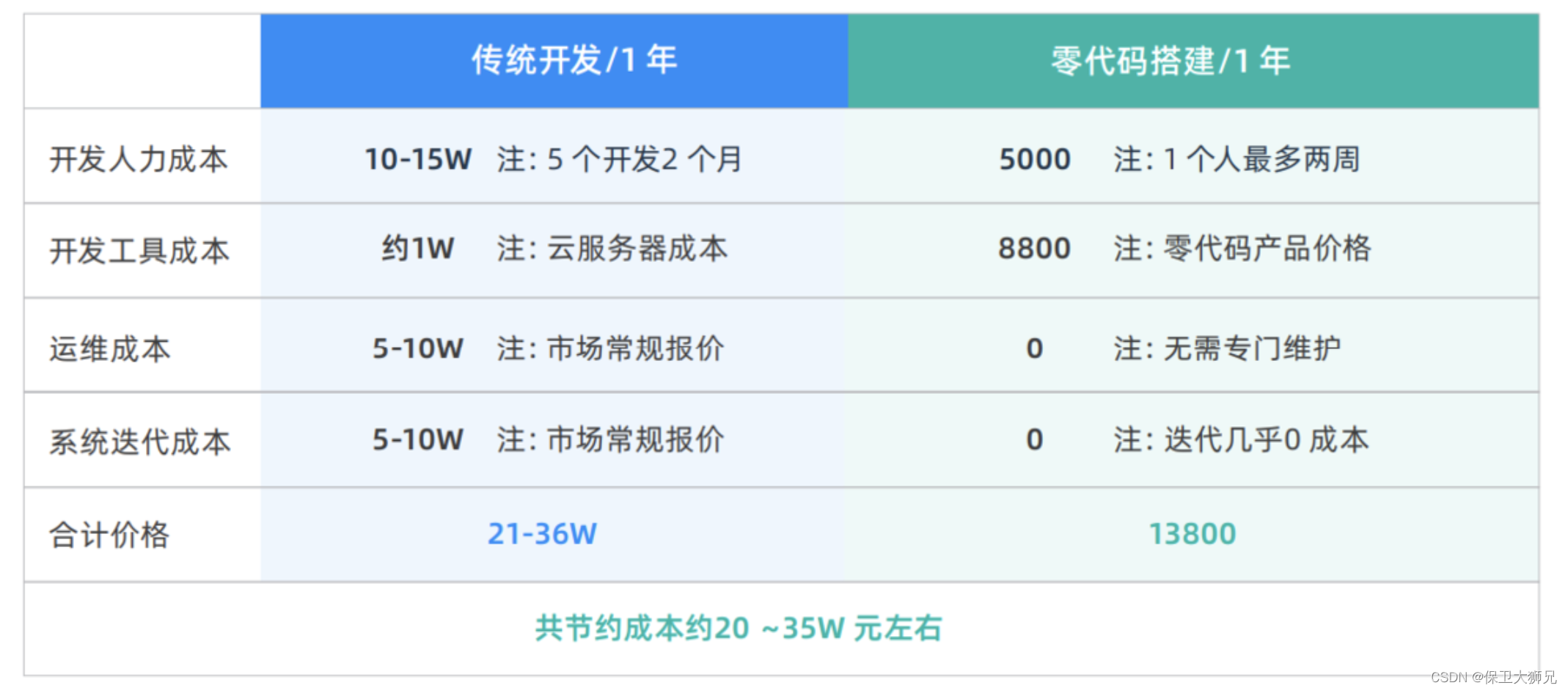
一文说透:低代码开发平台和零代码平台区别是什么?
低代码开发平台和零代码平台区别是什么? 一个简单的例子就可以解释清楚。 假设你想入住一套新房,回看住房变迁史: 最原始方式是:自己建造往后一点,交付“毛坯房”:开发商统一建小区,不需要自…...

4.将图神经网络应用于大规模图数据(Cluster-GCN)
到目前为止,我们已经为节点分类任务单独以全批方式训练了图神经网络。特别是,这意味着每个节点的隐藏表示都是并行计算的,并且可以在下一层中重复使用。 然而,一旦我们想在更大的图上操作,由于内存消耗爆炸,…...

pymongo更新数据
使用 PyMongo,可以通过以下步骤将查询到的记录进行更新: 下面是一个简单的示例代码片段,展示如何向名为users的集合中的所有文档添加一个新字段age。 import pymongo # 连接 MongoDB client pymongo.MongoClient("mongodb://localh…...
)
手机软件测试规范(含具体用例)
菜单基本功能测试规范一、短消息功能测试规范测试选项操作方法观察与判断结果创建、编辑短消息并发送书写短消息1、分别使用菜单或快捷方式进入书写短消息是否有异常; 2、输入0个字符,选择、输入号码发送,应成功; 3、输入1个中文…...

mysql having的用法
having的用法 having字句可以让我们筛选成组后的各种数据,where字句在聚合前先筛选记录,也就是说作用在group by和having字句前。而 having子句在聚合后对组记录进行筛选。我的理解就是真实表中没有此数据,这些数据是通过一些函数生存。 SQ…...
大数据需要学习哪些内容?
大数据技术的体系庞大且复杂,每年都会涌现出大量新的技术,目前大数据行业所涉及到的核心技术主要就是:数据采集、数据存储、数据清洗、数据查询分析和数据可视化。 Python 已成利器 在大数据领域中大放异彩 Python,成为职场人追求…...
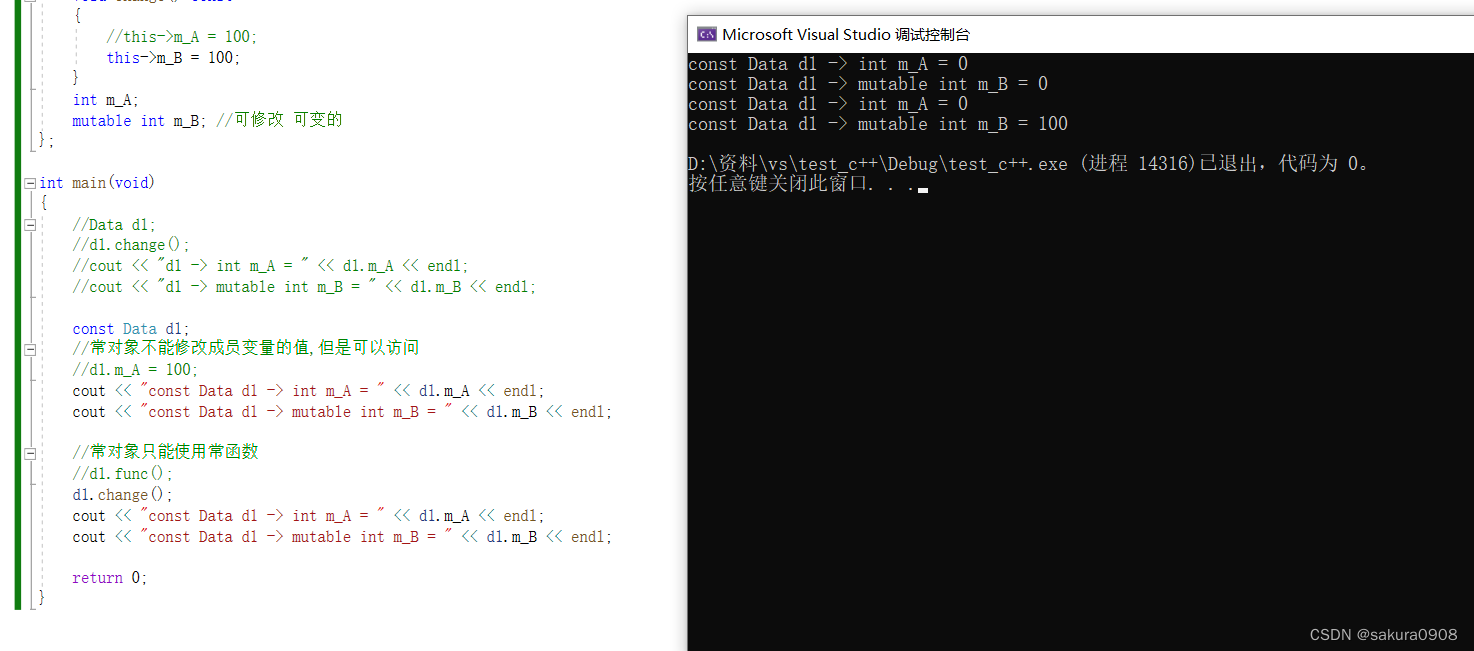
【c++】static和const修饰类的成员变量或成员函数
目录 1、静态成员变量 2、静态成员函数 3、常函数 4、常对象 当我们使用c的关键字static修饰类中的成员变量和成员函数的时候,此时的成员变量和成员函数被称为静态成员。 静态成员包含: 静态成员变量静态成员函数 1、静态成员变量 静态成员变量有…...
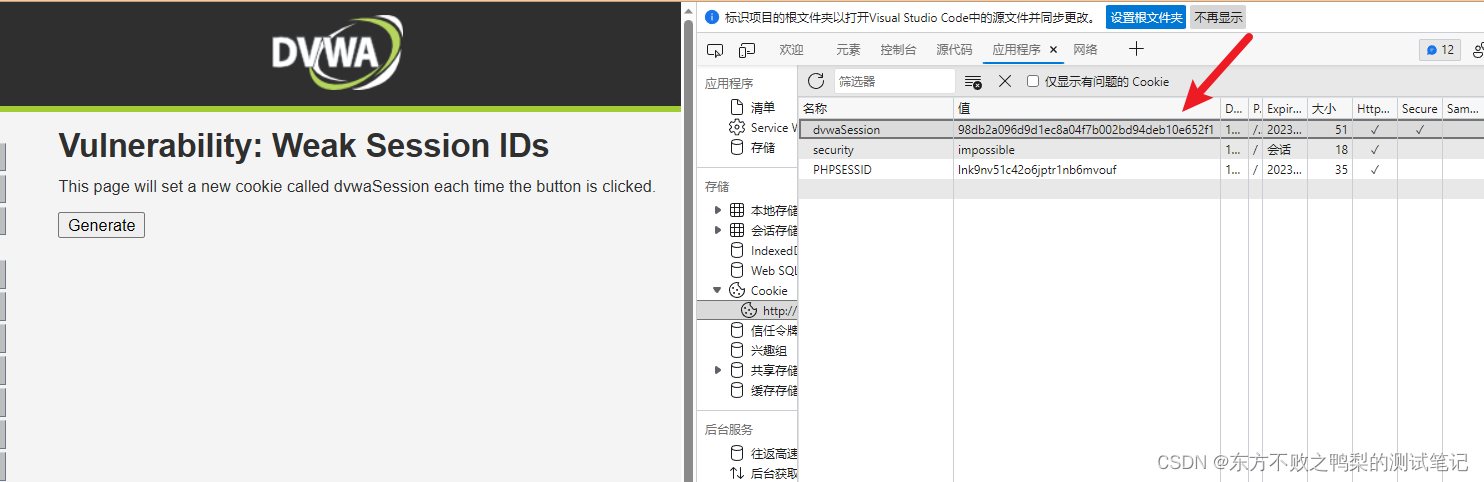
DVWA-9.Weak Session IDs
大约 了解会话 ID 通常是在登录后以特定用户身份访问站点所需的唯一内容,如果能够计算或轻松猜测该会话 ID,则攻击者将有一种简单的方法来访问用户帐户,而无需暴力破解密码或查找其他漏洞,例如跨站点脚本。 目的 该模块使用四种…...
Bug序列——容器内给/root目录777权限后无法使用ssh免密登录
Linux——创建容器并将本地调试完全的前后端分离项目打包上传docker运行_北岭山脚鼠鼠的博客-CSDN博客 接着上一篇文章结尾出现403错误时通过赋予/root目录以777权限解决403错误。 chmod 777 /root 现在又出现新的问题,远程ssh无法免密登录了,即使通过…...

华为OD机试真题 JavaScript 实现【服务中心选址】【2023Q1 100分 】
一、题目描述 一个快递公司希望在一条街道建立新的服务中心。公司统计了该街道中所有区域在地图上的位置,并希望能够以此为依据为新的服务中心选址,使服务中心到所有区域的距离的总和最小。 给你一个数组 positions,其中 positions[i] [le…...

<Linux>《OpenSSH 客户端配置文件ssh_config详解》
《OpenSSH 客户端配置文件ssh_config详解》 1、 ssh获取配置数据顺序2、关键字2.1 Host2.2 Match2.3 AddKeysToAgent2.4 AddressFamily2.5 BatchMode2.6 BindAddress2.7 BindInterface2.8 CanonicalDomains2.9 CanonicalizeFallbackLocal2.10 CanonicalizeHostname2.11 Canonic…...

Linux内核中内存管理相关配置项的详细解析8
接前一篇文章:Linux内核中内存管理相关配置项的详细解析7 十一、Enable KSM for page merging 对应配置变量为:CONFIG_KSM。 此项只有选中和不选中两种状态,默认为选中。 内核源码详细解释为: Enable Kernel Samepage Merging:…...

深入浅出Vite:Vite打包与拆分
一、背景 在生产环境下,为了提高页面加载性能,构建工具一般将项目的代码打包(bundle)到一起,这样上线之后只需要请求少量的 JS 文件,大大减少 HTTP 请求。当然,Vite 也不例外,默认情况下 Vite 利用底层打包引擎 Rollup 来完成项目的模块打包。 某种意义上来说,对线上环…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

第7篇:中间件全链路监控与 SQL 性能分析实践
7.1 章节导读 在构建数据库中间件的过程中,可观测性 和 性能分析 是保障系统稳定性与可维护性的核心能力。 特别是在复杂分布式场景中,必须做到: 🔍 追踪每一条 SQL 的生命周期(从入口到数据库执行)&#…...

实战三:开发网页端界面完成黑白视频转为彩色视频
一、需求描述 设计一个简单的视频上色应用,用户可以通过网页界面上传黑白视频,系统会自动将其转换为彩色视频。整个过程对用户来说非常简单直观,不需要了解技术细节。 效果图 二、实现思路 总体思路: 用户通过Gradio界面上…...
