华为OD机试真题 JavaScript 实现【服务中心选址】【2023Q1 100分 】

一、题目描述
一个快递公司希望在一条街道建立新的服务中心。公司统计了该街道中所有区域在地图上的位置,并希望能够以此为依据为新的服务中心选址,使服务中心到所有区域的距离的总和最小。
给你一个数组 positions,其中 positions[i] = [left, right] 表示第 i 区域在街道上的位置,其中left 代表区域的左侧的起点,right 代表区域的右侧终点。
假设服务中心的位置为 location:
- 如果第 i 个区域的右侧终点 right 满足 right< location,则第 i 个区域到服务中心的距离为location - right;
- 如果第 i 个区域的左侧起点 left 满足 left> location,则第 i 个区域到服务中心的距离为 left -location;
- 如果第 i 个区域的两侧 left,right 满足 left <= location <= right,则第 i 个区域到服务中心的距离为 0;
选择最佳的服务中心位置为 location,请返回最佳的服务中心位置到所有区域的距离总和的最小值;
二、输入描述
第一行,一个整数 N 表示区域个数;
后面 N 行,每行两个整数,表示区域的左右起点终点;
三、输出描述
运行结果输出一个整数,表示服务中心位置到所有区域的距离总和的最小值。
四、解题思路
- 首先读取输入的区域个数 N 和每个区域的左右起点终点;
- 创建一个二维数组 arr,用于存储每个区域的左右起点终点;
- 将每个区域的左右起点终点添加到一个临时列表 tmp 中;
- 对临时列表 tmp 进行排序,得到最小值和最大值;
- 初始化一个变量 ans,用于记录最小的距离总和,初始值设为最大值;
- 从最小值到最大值遍历所有可能的服务中心位置,步长为0.5;
- 对于每个服务中心位置 i,计算其到所有区域的距离总和 dis:
- 遍历每个区域的左右起点终点,判断服务中心位置与区域的相对位置关系;
- 如果区域的右侧终点小于服务中心位置 i,则距离为 i - r;
- 如果区域的左侧起点大于服务中心位置 i,则距离为 l - i;
- 如果服务中心位置在区域的范围内,则距离为 0;
- 将每个区域的距离累加到 dis 中;
- 更新最小的距离总和 ans,取当前计算得到的距离总和 dis 和 ans 中的较小值;
- 返回最小的距离总和 ans;
五、JavaScript算法源码
function getDistanceSum(n, arr) {const tmp = [];for (let i = 0; i < n; i++) {tmp.push(arr[i][0]);tmp.push(arr[i][1]);}tmp.sort((a, b) => a - b);const min = tmp[0];const max = tmp[tmp.length - 1];let ans = Infinity;for (let i = min; i <= max; i += 0.5) {let dis = 0;for (let j = 0; j < n; j++) {const l = arr[j][0];const r = arr[j][1];if (r < i) dis += i - r;else if (i < l) dis += l - i;}ans = Math.min(ans, dis);}return ans;
}
六、效果展示
1、输入
3
10 20
30 40
50 60
2、输出
30

🏆下一篇:华为OD机试真题 JavaScript 实现【相对开音节】【2022Q4 100分】,附详细解题思路
🏆本文收录于,华为OD机试(JavaScript)真题(A卷+B卷)
每一题都有详细的答题思路、详细的代码注释、样例测试,订阅后,专栏内的文章都可看,可加入华为OD刷题群(私信即可),发现新题目,随时更新,全天CSDN在线答疑。

相关文章:

华为OD机试真题 JavaScript 实现【服务中心选址】【2023Q1 100分 】
一、题目描述 一个快递公司希望在一条街道建立新的服务中心。公司统计了该街道中所有区域在地图上的位置,并希望能够以此为依据为新的服务中心选址,使服务中心到所有区域的距离的总和最小。 给你一个数组 positions,其中 positions[i] [le…...

<Linux>《OpenSSH 客户端配置文件ssh_config详解》
《OpenSSH 客户端配置文件ssh_config详解》 1、 ssh获取配置数据顺序2、关键字2.1 Host2.2 Match2.3 AddKeysToAgent2.4 AddressFamily2.5 BatchMode2.6 BindAddress2.7 BindInterface2.8 CanonicalDomains2.9 CanonicalizeFallbackLocal2.10 CanonicalizeHostname2.11 Canonic…...

Linux内核中内存管理相关配置项的详细解析8
接前一篇文章:Linux内核中内存管理相关配置项的详细解析7 十一、Enable KSM for page merging 对应配置变量为:CONFIG_KSM。 此项只有选中和不选中两种状态,默认为选中。 内核源码详细解释为: Enable Kernel Samepage Merging:…...

深入浅出Vite:Vite打包与拆分
一、背景 在生产环境下,为了提高页面加载性能,构建工具一般将项目的代码打包(bundle)到一起,这样上线之后只需要请求少量的 JS 文件,大大减少 HTTP 请求。当然,Vite 也不例外,默认情况下 Vite 利用底层打包引擎 Rollup 来完成项目的模块打包。 某种意义上来说,对线上环…...
大数据ETL工具Kettle
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言最近公司在搞大数据数字化,有MES,CIM,WorkFlow等等N多的系统,不同的数据源DB,需要将这些不同的数据源DB里的数据进行整治统一…...
大学物理(上)-期末知识点结合习题复习(4)——质点运动学-动能定理 力做功 保守力与非保守力 势能 机械能守恒定律 完全弹性碰撞
目录 1.力做功 恒力作用下的功 变力的功 2.动能定理 3.保守力与非保守力 4.势能 引力的功与弹力的功 引力势能与弹性势能 5.保守力做功与势能的关系 6.机械能守恒定律 7.完全弹性碰撞 题1 题目描述 题解 题2 题目描述 题解 1.力做功 物体在力作用下移动做功…...
这两个小众的资源搜索工具其实很好用
01 小不点搜索是一个中国网络技术公司开发的网盘搜索引擎,该网站通过与多个主流网盘进行整合,为用户提供一种快速查找和下载文件的方式。小不点搜索因其高效性、便利性和实用性受到了广大用户的喜爱。 在技术实现上,小不点搜索拥有先进的搜…...
— 单例模式1)
Java设计模式(六)— 单例模式1
系列文章目录 单例模式介绍 单例模式之静态常量饿汉式 单例模式之静态代码饿汉式 单例模式之线程不安全懒汉式 文章目录 系列文章目录前言一、单例设计模式介绍二、单例设计模式八种方式三、单例—静态常量饿汉式1.静态常量饿汉式介绍2.静态常量饿汉式案例3.静态常量饿汉式优缺…...
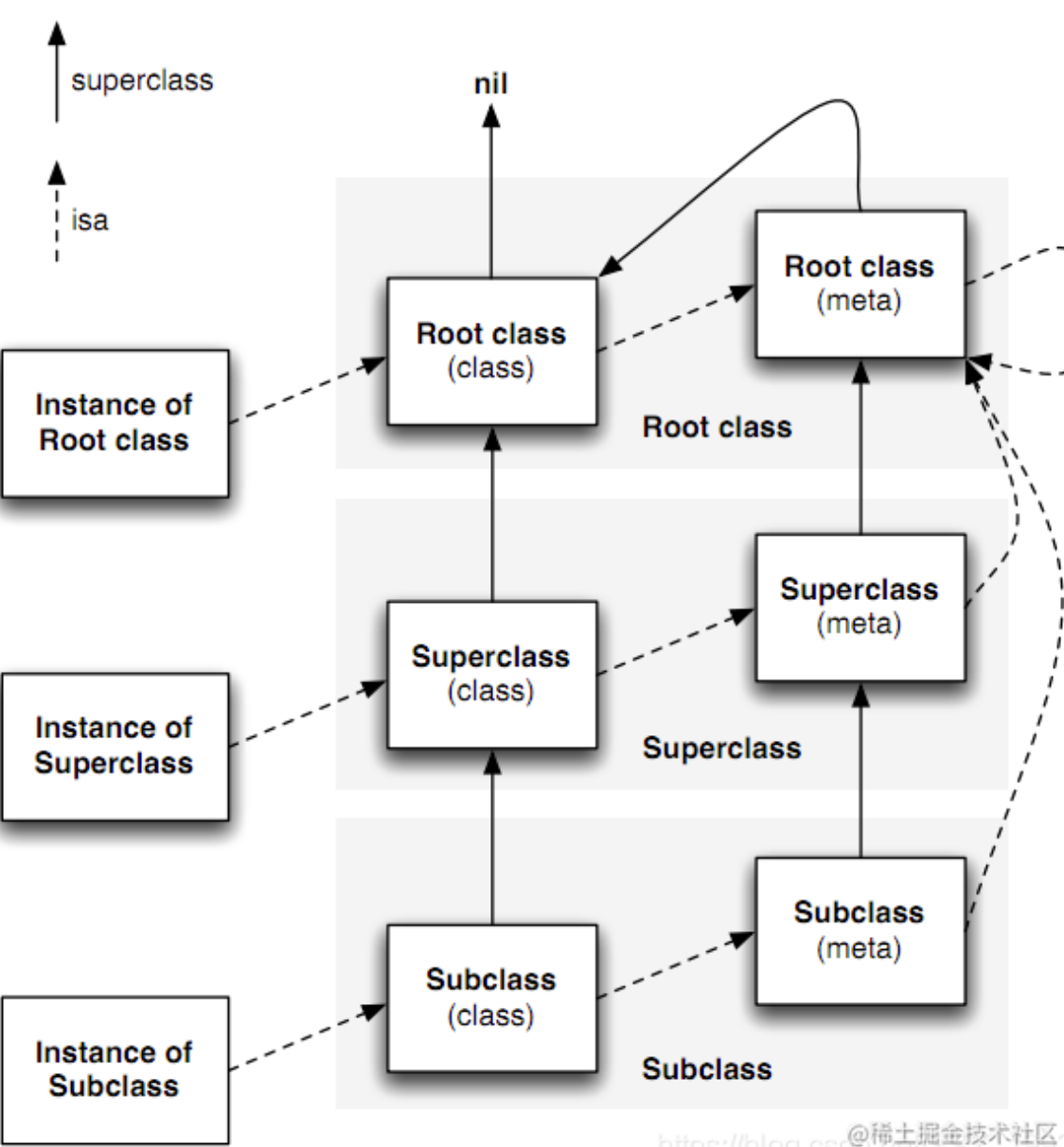
iOS -- isa指针
isa指针:isa指针是一个指向对象所属类或元类的指针。它决定了对象可以调用的方法和属性。isa指针在对象的结构中存在,并且在运行时会被自动设置。isa 指针,表示这个对象是一个什么类。而 Class 类型, 也就是 struct objc_class * …...

【SA8295P 源码分析】14 - Passthrough配置文件 /mnt/vm/images/linux-la.config 内容分析
系列文章汇总见:《【SA8295P 源码分析】00 - 系列文章链接汇总》 本文链接:《【SA8295P 源码分析】14 - Passthrough配置文件 /mnt/vm/images/linux-la.config 内容分析》 透传配置文件位于:qnx.git\apps\qnx_ap\target\hypervisor\gvm\ivi\la\linux-la.config 它是在QNX Ho…...
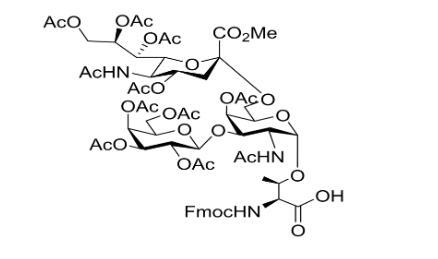
新型糖基化氨基酸:Fmoc-Thr((Ac4Galβ1-3)Me,Ac4Neu5Acα2-6AcGalNAcα)-OH,化学CAS号174783-92-7
●英文名:Fmoc-Thr((Ac4Galβ1-3)Me,Ac4Neu5Acα2-6AcGalNAcα)-OH ●外观以及性质: Fmoc-Thr((Ac4Galβ1-3)Me,Ac4Neu5Acα2-6AcGalNAcα)-OH中通过对蛋白进行复杂蛋白糖基化修饰,细胞产生了极大丰度的蛋白质类型;通过对各类糖基…...

网络安全(黑客)怎么自学?
最近看到很多问题,都是小白想要转行网络安全行业咨询学习路线和学习资料的,作为一个培训机构,学习路线和免费学习资料肯定是很多的。机构里面的不是顶级的黑阔大佬就是正在学习的同学,也用不上这些内容,每天都在某云盘…...

Vue学习 之 MacOS 安装 webpack
Vue学习 之 MacOS 安装 webpack webpack 简介 Webpack 是一个非常流行的前端构建工具,它可以将多个模块(包括CSS、JavaScript、图片等)打包成一个或多个静态资源文件(bundle),以便用于部署到生产环境。We…...

媒介易教你海外品牌推广:如何选择适合的新闻通稿发布平台?
在进行海外品牌推广时,选择合适的海外新闻通稿发布第三方平台是提高品牌曝光度和影响力的重要一环。这些平台可以帮助企业将新闻内容传播到全球范围内的媒体和受众,为品牌推广提供更广阔的机会。然而,选择合适的发布平台并不容易,…...

网络安全的学习路线是怎么样的?
最近看到网上有很多人在问诸如:“怎样成为网络安全工程师”等相关问题,这可能与近几年网络安全事件频发,国家对于互联网信息安全和互联网舆情的重视程度不断提升有关,网络信息安全工程师随之成为炙手可热的职业。关于职业前景的详…...

QT学习07:五种按钮控件
文章首发于我的个人博客:欢迎大佬们来逛逛 文章目录 抽象类:QAbstractButtonQPushButtonQToolButtonQCommandLinkButtonQRadioButtonQCheckBoxQButtonGroup 抽象类:QAbstractButton 是所有按钮类的祖先。 QAbstractButton的信号:…...

chatgpt赋能python:Python如何截图运行结果
Python如何截图运行结果 介绍 Python是一种高级编程语言,非常流行。它具有许多有用的功能和库,使其成为许多开发人员的首选编程语言之一。但是,当您运行Python程序并需要与他人共享结果时,您可能需要截图运行结果。在本文中&…...
)
Baumer工业相机堡盟工业相机如何通过BGAPISDK使用JPEG图像压缩功能(C#)
Baumer工业相机堡盟工业相机如何通过BGAPISDK使用JPEG图像压缩功能(C#) Baumer工业相机Baumer工业相机BGAPISDK和JPEG图像压缩功能的技术背景Baumer工业相机通过BGAPISDK使用JPEG图像压缩功能1.引用合适的类文件2.使用BGAPISDK设置堡盟相机JPEG图像压缩模…...

RT-Thread FAL组件
目录 1、FAL介绍2、使用FAL2.1 下载FAL软件包2.2 FAL移植2.2.1 定义flash设备2.2.2 定义flash设备表&分区表2.2.3 加入到mdk工程3、MSH测试1、FAL介绍 FAL(Flash Abstraction Layer) Flash抽象层,是对Flash及基于Flash的分区进行管理、操作的抽象层,对上层统一了Flash及分…...
【git切换分支/tag】git stash保存暂不提交的更改
目录 问题git stash使用方法git stash pop 还原修改 git stash使用、修改指定tag的代码 其他git指令 问题 情景:分支1上开发新功能,临时切换到其他分支或tag上修改bug。 1、直接切换:如果没有冲突,分支1的修改会带到要切换的分支…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...
