【IoU全总结】GIoU, DIoU, CIoU, EIoUFocal, αIoU, SIoU,WIoU【基础收藏】
🥑 Welcome to Aedream同学 's blog! 🥑
并不存在效果一定优秀的IoU,需要结合自己的网络、数据集试验。
不想深究原理可直接跳转总结。文内公式均为手打,非图片,方便查看
文章目录
- L1 Loss,L2Loss,smooth L1 loss
- L1 Loss
- L2 Loss
- SmoothL1Loss
- IoU
- GIoU(CVPR2019)
- DIoU(AAAI2020)
- CIoU(AAAI2020)
- EIoU&Focal(arXiv2021)
- αIoU(NeurlPS2021)
- SIoU(arXiv2022)
- WIoU
- 总结
- 原论文
- 代码
目标检测任务的损失函数一般都有Classificition Loss(分类损失函数)和Bounding Box Regeression Loss(回归损失函数)。子任务分别需要对应损失函数的反传来学习。
因此,更好的定位有利于模型精度的提高。
L1 Loss,L2Loss,smooth L1 loss
在IoU Loss提出来之前,检测上有关候选框的回归主要是通过坐标的回归损失来优化。
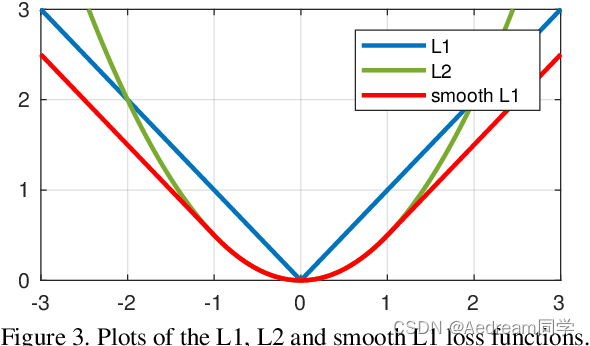

L1 Loss
- L1 范数损失
- 最小绝对值偏差(LAD)
- 最小绝对值误差(LAE)
最常看到的MAE也是指L1 Loss损失函数。 它是把目标值 y i y_i yi与模型输出(估计值) f ( x i ) f(x_i) f(xi) 做绝对值得到的误差。
l o s s ( x , y ) = 1 n ∑ i = 1 n ∣ y i − f ( x i ) ∣ loss(x,y)=\frac{1}{n}\sum_ {i=1}^n \left|y_i-f(x_i) \right| loss(x,y)=n1∑i=1n∣yi−f(xi)∣
什么时候使用?
- 回归任务
- 简单的模型
- 由于神经网络通常是解决复杂问题,所以很少使用。

L2 Loss
- L2 范数损失
- 最小均方值偏差(LSD)
- 最小均方值误差(LSE)
最常看到的MSE也是指L2 Loss损失函数,PyTorch中也将其命名为torch.nn.MSELoss
它是把目标值 y i y_i yi 与模型输出(估计值) f ( x i ) f(x_i) f(xi) 做差然后平方得到的误差
l o s s ( x , y ) = 1 n ∑ i = 1 n ( y i − f ( x i ) ) 2 loss(x,y)=\frac{1}{n} \sum_{i=1}^n(y_i-f(x_i))^2 loss(x,y)=n1∑i=1n(yi−f(xi))2
什么时候使用?
- 回归任务
- 数值特征不大
- 问题维度不高

SmoothL1Loss
简单来说就是平滑版的L1 Loss。
SoothL1Loss的函数如下:
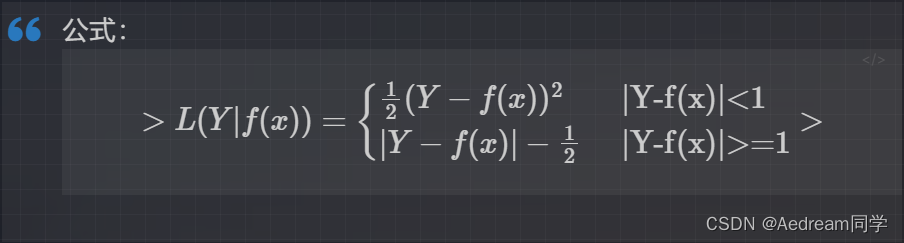
仔细观察可以看到,当预测值和ground truth差别较小的时候(绝对值差小于1),其实使用的是L2 Loss;而当差别大的时候,是L1 Loss的平移。SooothL1Loss其实是L2Loss和L1Loss的结合,它同时拥有L2 Loss和L1 Loss的部分优点。
1. 当预测值和ground truth差别较小的时候(绝对值差小于1),梯度不至于太大。(损失函数相较L1 Loss比较圆滑)
2. 当差别大的时候,梯度值足够小(较稳定,不容易梯度爆炸)。
什么时候使用?
- 回归
- 当特征中有较大的数值
- 适合大多数问题
但L1 Loss和L2 Loss存在比较大的问题:
L1 Loss的问题: 损失函数对x的导数为常数,在训练后期,x很小时,如果learning rate 不变,损失函数会在稳定值附近波动,很难收敛到更高的精度。
L2 Loss的问题: 损失函数对x的导数在x值很大时,其导数也非常大,在训练初期不稳定。
而且,基于L1/L2 Loss的坐标回归不具有尺度不变性,且并没有将四个坐标之间的相关性考虑进去。因此,像L1/L2 Loss直接的坐标回归实际上很难描述两框之间的相对位置关系。

IoU
因此,在ACM2016的论文中提出了IoU loss,它将四个坐标点看成一个整体进行计算,具有尺度不变性(也就是对尺度不敏感)。IoU Loss的定义是先求出预测框和真实框之间的交集和并集之比,再求负对数,但是在实际使用中我们常常将IoU Loss写成1-IoU。如果两个框重合则交并比等于1,Loss为0说明重合度非常高。因此,IoU的取值范围为[0,1]。
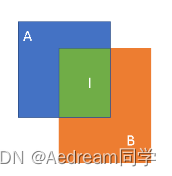
I O U = ( A ∩ B ) ( A ∪ B ) IOU = \frac{(A\cap B)}{(A\cup B)} IOU=(A∪B)(A∩B)
I O U L o s s = 1 − I O U IOU Loss = 1 - IOU IOULoss=1−IOU
虽然IoU Loss虽然解决了Smooth L1系列变量相互独立和不具有尺度不变性的两大问题,但是它也存在两个问题:
- 当预测框和目标框不相交时,即IoU(A,B)=0时,不能反映A,B距离的远近此时损失函数不可导,IoU Loss 无法优化两个框不相交的情况。
- 假设预测框和目标框的大小都确定,只要两个框的相交值是确定的,即其IoU值相同时,IoU值不能反映两个框是如何相交的。

GIoU(CVPR2019)
针对IoU无法反映两个框是如何相交的问题,GIoU通过引入预测框和真实框的最小外接矩形(类似于图像处理中的闭包区域)来获取预测框、真实框在闭包区域中的比重。这样子,GIoU不仅可以关注重叠区域,还可以关注其他非重合区域,能比较好的反映两个框在闭包区域中的相交情况。
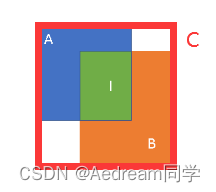
G I o U = I o U − ∣ C − ( A ∪ B ) ∣ ∣ C ∣ GIoU = IoU - \frac{|C- (A\cup B)|}{|C|} \\ GIoU=IoU−∣C∣∣C−(A∪B)∣
从公式上来看,GIoU是一种IoU的下界,取值范围[-1,1]。在两者重合的时候取最大值1,在两者无交集且无限远的时候取最小值-1。因此,与IoU相比,GIoU是一个比较好的距离度量指标。
虽然GIoU通过引入闭包区域缓解了预测框与真实框相交位置的衡量问题,但其实际上仍存在两个问题:
- 对每个预测框与真实框均要去计算最小外接矩形,计算及收敛速度受到限制
- 当预测框在真实框内部时,GIoU退化为IoU,也无法区分相对位置关系

DIoU(AAAI2020)
DIoU在IoU的基础上直接回归两个框中心点的欧式距离,加速了收敛速度。DIoU的惩罚项是基于中心点的距离和对角线距离的比值。这样就避免了GIoU在两框距离较远时产生较大闭包时所造成的Loss值较大而难以优化的情况。
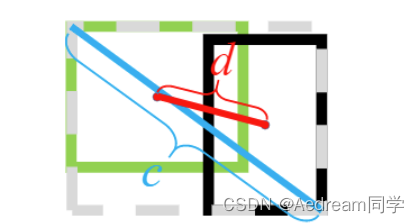
L D I O U = 1 − I O U + ρ 2 ( b , b g t ) C 2 L_{DIOU} = 1 - IOU + \frac{\rho^{2}(b,b^{gt})}{C^{2}} LDIOU=1−IOU+C2ρ2(b,bgt)
虽然DIOU能够直接最小化预测框和真实框的中心点距离加速收敛,但是Bounding box的回归还有一个重要的因素纵横比暂未考虑。

CIoU(AAAI2020)
虽然DIoU Loss通过中心点回归缓解了两框距离较远时难优化的问题,但DIoU Loss仍存在两框中心点重合,但宽高比不同时,DIoU Loss退化为IoU Loss的问题。因此,为了得到更加精准的预测框,CIoU在DIoU的基础上增加了一个影响因子,即增加了预测框与真实框之间长宽比的一致性的考量。
CIOU的惩罚项是在DIOU的惩罚项基础上加了一个影响因子 α υ \alpha\upsilon αυ,这个因子把预测框纵横比拟合真实框的纵横比考虑进去。惩罚项公式如下:
R C I O U = ρ 2 ( b , b g t ) c 2 + α υ R_{CIOU} =\frac{\rho^{2}\left( b,b^{gt} \right)}{c^{2}} + \alpha\upsilon RCIOU=c2ρ2(b,bgt)+αυ
其中 α \alpha α 是用于做trade-off的参数, α \alpha α 的定义如下:
α = υ ( 1 − I O U ) + υ \alpha= \frac{\upsilon}{\left( 1-IOU \right)+\upsilon} α=(1−IOU)+υυ
υ \upsilon υ 是用来衡量长宽比一致性的参数, υ \upsilon υ定义如下:
υ = 4 π 2 ( a r c t a n w g t h g t − a r c t a n w h ) 2 \upsilon=\frac{4}{\pi^{2}}\left( arctan\frac{w^{gt}}{h^{gt}} - arctan\frac{w}{h} \right)^{2} υ=π24(arctanhgtwgt−arctanhw)2
完整的CIOU损失函数的公式如下:
L C I O U = 1 − I O U + ρ 2 ( b , b g t ) c 2 + α υ L_{CIOU} = 1- IOU +\frac{\rho^{2}\left( b,b^{gt} \right)}{c^{2}} + \alpha\upsilon LCIOU=1−IOU+c2ρ2(b,bgt)+αυ
CIOU Loss的梯度在长宽 [ 0 , 1 ] [0,1] [0,1]的情况下, w 2 + h 2 w^{2}+h^{2} w2+h2的值通常很小,会导致梯度爆炸,因此在 1 w 2 + h 2 \frac{1}{w^{2}+h^{2}} w2+h21 实现时将替换成1。

EIoU&Focal(arXiv2021)
EIoU在CIoU的基础上将长宽比拆开,明确地衡量了三个几何因素的差异,即重叠区域、中心点和边长,同时引入Fcoal loss解决了难易样本不平衡的问题。
EIOU的惩罚项是在CIOU的惩罚项基础上将纵横比的影响因子拆开分别计算目标框和锚框的长和宽,该损失函数包含三个部分:重叠损失,中心距离损失,宽高损失,前两部分延续CIOU中的方法,但是宽高损失直接使目标盒与锚盒的宽度和高度之差最小,使得收敛速度更快。惩罚项公式如下:
L E I O U = L I O U + L d i s + L a s p = 1 − I O U + ρ 2 ( b , b ft ) c 2 + ρ 2 ( w , w g t ) C w 2 + ρ 2 ( h , h g t ) C h 2 L_{EIOU}=L_{IOU}+L_{dis}+L_{asp}\\ =1-IOU+\dfrac{\rho^{2}(\mathbf{b},\mathbf{b}^{\text{ft}})}{c^{2}}+\dfrac{\rho^2(w,w^{gt})}{C_{w}^{2}}+\frac{\rho^2(h,h^{gt})}{C_{h}^{2}} LEIOU=LIOU+Ldis+Lasp=1−IOU+c2ρ2(b,bft)+Cw2ρ2(w,wgt)+Ch2ρ2(h,hgt)
其中 Cw 和 Ch 是覆盖两个Box的最小外接框的宽度和高度。
考虑到BBox的回归中也存在训练样本不平衡的问题,即在一张图像中回归误差小的高质量锚框的数量远少于误差大的低质量样本,质量较差的样本会产生过大的梯度影响训练过程。作者在EIOU的基础上结合Focal Loss提出一种Focal EIOU Loss,梯度的角度出发,把高质量的锚框和低质量的锚框分开,惩罚项公式如下:
L Focal-EIOU = I O U γ L E I o U L_{\text{Focal-EIOU}}=IOU^\gamma L_{EIoU} LFocal-EIOU=IOUγLEIoU
γ为控制异常值抑制程度的参数。该损失中的Focal与传统的Focal Loss有一定的区别,传统的Focal Loss针对越困难的样本损失越大,起到的是困难样本挖掘的作用;而根据上述公式:IOU越高的损失越大,相当于加权作用,给越好的回归目标一个越大的损失,有助于提高回归精度。
两个优化方法:
- 将纵横比的损失项拆分成预测的宽高分别与最小外接框宽高的差值,加速了收敛提高了回归精度;
- 引入了Focal Loss优化了边界框回归任务中的样本不平衡问题,即减少与目标框重叠较少的大量锚框对BBox 回归的优化贡献,使回归过程专注于高质量锚框。
不足之处或许在于Focal的表达形式是否有待改进。

αIoU(NeurlPS2021)
αIoU将现有的基于IoU 的损失进行了一个推广。使得αIoU可以显著超越现有的基于 IoU 的损失,通过调节α,使探测器更灵活地实现不同水平的bbox回归精度,并且αIoU对小数据集和噪声的鲁棒性更强
L IoU = 1 − I o U ⟹ L α − IoU = 1 − I o U α , \mathcal L_{\text{IoU}}=1-IoU\Longrightarrow\mathcal L_{\alpha-\text{IoU}}=1-IoU^{\alpha}, LIoU=1−IoU⟹Lα−IoU=1−IoUα,
L G b b U = 1 − I o U + ∣ C − ( B ∪ B g t ) ∣ ∣ C ∣ ⟹ L α G b l d U = 1 − I o U α + ( ∣ C − ( B ∪ B g t ) ∣ ∣ C ∣ ) α , {\cal L}_{\mathrm{GbbU}}=1-I o U+{\frac{|C-(B\cup B^{g t})|}{|C|}}\Longrightarrow{\cal L}_{\alpha\mathrm{Gbld}U}=1-I o U^{\alpha}+({\frac{|C-({B\cup B^{g t}})|}{|C|}})^{\alpha}, LGbbU=1−IoU+∣C∣∣C−(B∪Bgt)∣⟹LαGbldU=1−IoUα+(∣C∣∣C−(B∪Bgt)∣)α,
其余同理……

SIoU(arXiv2022)
传统的目标检测损失函数依赖于边界框回归指标的聚合,例如预测框和真实框(即 GIoU、CIoU、ICIoU 等)的距离、重叠区域和纵横比。然而,迄今为止提出和使用的方法都没有考虑期望的真实框和预测框之间不匹配的方向。这种不足导致收敛速度较慢且效率较低,因为预测框在训练过程中可能会“四处游荡”,最终会产生一个更差的模型。
SIoU提出了一种新的损失函数,重新定义了惩罚度量,考虑了期望回归之间的向量夹角。
SIoU损失函数由4个成本函数组成
Angle cost
Λ = 1 − 2 ∗ s i n 2 ( a r c s i n ( x ) − π 4 ) , \Lambda=1-2*sin^2\left(arcsin\left(x\right)-\frac{\pi}{4}\right), Λ=1−2∗sin2(arcsin(x)−4π),
Distance cost
Δ = ∑ t = x , y ( 1 − e − γ ρ t ) , \Delta=\sum_{t=x,y}(1-e^{-\gamma\rho_t}), Δ=∑t=x,y(1−e−γρt),
ρ x = ( b c x g t − b c x c W ) 2 , ρ y = ( b c y g t − b c y c h ) 2 , γ = 2 − Λ \rho_{x}=\left({\frac{b_{c x}^{g t}-b_{c x}}{c_{W}}}\right)^{2},\rho_{y}=\left({\frac{{b_{c y}^{g t}}-{b_{c y}}}{{c_{h}}}}\right)^{2},\gamma=2-\Lambda ρx=(cWbcxgt−bcx)2,ρy=(chbcygt−bcy)2,γ=2−Λ
Shape cost
Ω = ∑ t = w , h ( 1 − e − ω t ) θ \Omega=\sum\limits_{t=w,h}(1-e^{-\omega_t})^{\theta} Ω=t=w,h∑(1−e−ωt)θ
IoU cost
L b o x = 1 − I o U + Δ + Ω 2 L_{box}=1-IoU+\dfrac{\varDelta+\Omega}{2} Lbox=1−IoU+2Δ+Ω

WIoU
Focal EIoU v1被提出来解决质量较好和质量较差的样本间的BBR平衡问题,但由于其静态聚焦机制(FM),非单调FM的潜力没有被充分利用,基于这一思想,作者提出了一种基于IoU的损失,该损失具有动态非单调FM,名为Wise IoU(WIoU)。
主要贡献总结如下:
提出了BBR的基于注意力的损失WIoU v1,它在仿真实验中实现了比最先进的SIoU更低的回归误差。
设计了具有单调FM的WIoU v2和具有动态非单调FM的WIoU v3。利用动态非单调FM的明智的梯度增益分配策略,WIoU v3获得了优越的性能。
对低质量的样本的影响进行了一系列详细的研究,证明了动态非单调调频的有效性和效率。
由于训练数据不可避免地包含低质量示例,几何因素(如距离和纵横比)将加重对低质量示例的惩罚,从而降低模型的泛化性能。当anchor box与目标box很好地重合时,一个好的损失函数应该会削弱几何因素的惩罚,而较少的训练干预将使模型获得更好的泛化能力。
WIoU v1
L W I d U 1 = R W I d U L I d U R W I d U = exp ( ( x − x g t ) 2 + ( y − y g t ) 2 ( W g 2 + H g 2 ) ∗ ) \mathcal L_{WIdU1}=\mathcal R_{WIdU}\mathcal L_{IdU}\\ \mathcal R_{WIdU}=\exp(\dfrac{(x-x_{gt})^2+(y-y_{gt})^2}{(W_g^2+H_g^2)^*}) LWIdU1=RWIdULIdURWIdU=exp((Wg2+Hg2)∗(x−xgt)2+(y−ygt)2)
WIoU v2
L W I o U v 2 = ( L I o U ∗ L ‾ I o U ‾ ) γ L W I o U v 1 \mathcal{L}_{WIoUv2}=(\dfrac{\mathcal{L}_{IoU}^*}{\overline{\overline{\mathcal{L}}_{IoU}}})^\gamma\mathcal{L}_{WIoUv1} LWIoUv2=(LIoULIoU∗)γLWIoUv1
WIoU v3
β = L I o U ∗ L I o U ‾ ∈ [ 0 , + ∞ ) \beta=\dfrac{\mathcal{L}^{*}_{IoU}}{\overline{\mathcal{L}_{IoU}}}\in[0,+\infty) β=LIoULIoU∗∈[0,+∞)L W I o U v 3 = r L W I o U v 1 , r = β δ α β − δ \mathcal{L}_{WIoUv3}=r\mathcal{L}_{WIoUv1},r=\dfrac{\beta}{\delta\alpha^{\beta-\delta}} LWIoUv3=rLWIoUv1,r=δαβ−δβ

总结
边界框回归的三大几何因素:重叠面积、中心点距离、纵横比
- IOU Loss:考虑了重叠面积,归一化坐标尺度;
- GIOU Loss:考虑了重叠面积,基于IOU解决边界框不相交时loss等于0的问题;
- DIOU Loss:考虑了重叠面积和中心点距离,基于IOU解决GIOU收敛慢的问题;
- CIOU Loss:考虑了重叠面积、中心点距离、纵横比,基于DIOU提升回归精确度;
- EIOU Loss:考虑了重叠面积,中心点距离、长宽边长真实差,基于CIOU解决了纵横比的模糊定义,并添加Focal Loss解决BBox回归中的样本不平衡问题。
- α-IOU Loss:通过调节α,使探测器更灵活地实现不同水平的bbox回归精度
- SIOU Loss:考虑到期望回归之间向量的角度,重新定义角度惩罚度量,它可以使预测框快速漂移到最近的轴,随后则只需要回归一个坐标(X或Y),这有效地减少了自由度的总数。
- WIOU Loss:解决质量较好和质量较差的样本间的BBR平衡问题
| IOU Loss | GIOU Loss | DIOU Loss | CIOU Loss | EIOU Loss | |
|---|---|---|---|---|---|
| 优点 | IOU算法是目标检测中最常用的指标,具有尺度不变性,满足非负性;同一性;对称性;三角不等性等特点。 | GIOU在基于IOU特性的基础上引入最小外接框解决检测框和真实框没有重叠时loss等于0问题。 | DIOU在基于IOU特性的基础上考虑到GIOU的缺点,直接回归两个框中心点的欧式距离,加速收敛。 | CIOU就是在DIOU的基础上增加了检测框尺度的loss,增加了长和宽的loss,这样预测框就会更加的符合真实框。 | EIOU在CIOU的基础上分别计算宽高的差异值取代了纵横比,同时引入Focal Loss解决难易样本不平衡的问题。 |
| 缺点 | 1.如果两个框不相交,不能反映两个框距离远近 2.无法精确的反映两个框的重合度大小 | 1.当检测框和真实框出现包含现象的时候GIOU退化成IOU 2.两个框相交时,在水平和垂直方向上收敛慢 | 回归过程中未考虑Bounding box的纵横比,精确度上尚有进一步提升的空间 | 1. 纵横比描述的是相对值,存在一定的模糊 2. 未考虑难易样本的平衡问题 | 聚焦机制是静态的,并未充分挖掘非单调聚焦机制的潜能 |
原论文
IoU loss
论文:《UnitBox: An Advanced Object Detection Network》
GIoU loss
论文:《Generalized Intersection over Union: A Metric and A Loss for Bounding Box Regression》
DIoU/CIoU
论文:《Distance-IoU Loss: Faster and Better Learning for Bounding Box Regression》
EIoU Loss/Focal EIoU Loss
论文:Focal and Efficient IOU Loss for Accurate Bounding Box Regression》
SIoU loss
论文:《SIoU Loss: More Powerful Learning for Bounding Box Regression》
WIoU loss
论文:《Wise-IoU: Bounding Box Regression Loss with Dynamic Focusing Mechanism》
代码
代码如下:
class WIoU_Scale:''' monotonous: {None: origin v1True: monotonic FM v2False: non-monotonic FM v3}momentum: The momentum of running mean'''iou_mean = 1.monotonous = False_momentum = 1 - 0.5 ** (1 / 7000)_is_train = Truedef __init__(self, iou):self.iou = iouself._update(self)@classmethoddef _update(cls, self):if cls._is_train: cls.iou_mean = (1 - cls._momentum) * cls.iou_mean + \cls._momentum * self.iou.detach().mean().item()@classmethoddef _scaled_loss(cls, self, gamma=1.9, delta=3):if isinstance(self.monotonous, bool):if self.monotonous:return (self.iou.detach() / self.iou_mean).sqrt()else:beta = self.iou.detach() / self.iou_meanalpha = delta * torch.pow(gamma, beta - delta)return beta / alphareturn 1def bbox_iou(box1, box2, xywh=True, GIoU=False, DIoU=False, CIoU=False, SIoU=False, EIoU=False, WIoU=False, Focal=False, alpha=1, gamma=0.5, scale=False, eps=1e-7):# Returns Intersection over Union (IoU) of box1(1,4) to box2(n,4)# Get the coordinates of bounding boxesif xywh: # transform from xywh to xyxy(x1, y1, w1, h1), (x2, y2, w2, h2) = box1.chunk(4, -1), box2.chunk(4, -1)w1_, h1_, w2_, h2_ = w1 / 2, h1 / 2, w2 / 2, h2 / 2b1_x1, b1_x2, b1_y1, b1_y2 = x1 - w1_, x1 + w1_, y1 - h1_, y1 + h1_b2_x1, b2_x2, b2_y1, b2_y2 = x2 - w2_, x2 + w2_, y2 - h2_, y2 + h2_else: # x1, y1, x2, y2 = box1b1_x1, b1_y1, b1_x2, b1_y2 = box1.chunk(4, -1)b2_x1, b2_y1, b2_x2, b2_y2 = box2.chunk(4, -1)w1, h1 = b1_x2 - b1_x1, (b1_y2 - b1_y1).clamp(eps)w2, h2 = b2_x2 - b2_x1, (b2_y2 - b2_y1).clamp(eps)# Intersection areainter = (b1_x2.minimum(b2_x2) - b1_x1.maximum(b2_x1)).clamp(0) * \(b1_y2.minimum(b2_y2) - b1_y1.maximum(b2_y1)).clamp(0)# Union Areaunion = w1 * h1 + w2 * h2 - inter + epsif scale:self = WIoU_Scale(1 - (inter / union))# IoU# iou = inter / union # ori iouiou = torch.pow(inter/(union + eps), alpha) # alpha iouif CIoU or DIoU or GIoU or EIoU or SIoU or WIoU:cw = b1_x2.maximum(b2_x2) - b1_x1.minimum(b2_x1) # convex (smallest enclosing box) widthch = b1_y2.maximum(b2_y2) - b1_y1.minimum(b2_y1) # convex heightif CIoU or DIoU or EIoU or SIoU or WIoU: # Distance or Complete IoU https://arxiv.org/abs/1911.08287v1c2 = (cw ** 2 + ch ** 2) ** alpha + eps # convex diagonal squaredrho2 = (((b2_x1 + b2_x2 - b1_x1 - b1_x2) ** 2 + (b2_y1 + b2_y2 - b1_y1 - b1_y2) ** 2) / 4) ** alpha # center dist ** 2if CIoU: # https://github.com/Zzh-tju/DIoU-SSD-pytorch/blob/master/utils/box/box_utils.py#L47v = (4 / math.pi ** 2) * (torch.atan(w2 / h2) - torch.atan(w1 / h1)).pow(2)with torch.no_grad():alpha_ciou = v / (v - iou + (1 + eps))if Focal:return iou - (rho2 / c2 + torch.pow(v * alpha_ciou + eps, alpha)), torch.pow(inter/(union + eps), gamma) # Focal_CIoUelse:return iou - (rho2 / c2 + torch.pow(v * alpha_ciou + eps, alpha)) # CIoUelif EIoU:rho_w2 = ((b2_x2 - b2_x1) - (b1_x2 - b1_x1)) ** 2rho_h2 = ((b2_y2 - b2_y1) - (b1_y2 - b1_y1)) ** 2cw2 = torch.pow(cw ** 2 + eps, alpha)ch2 = torch.pow(ch ** 2 + eps, alpha)if Focal:return iou - (rho2 / c2 + rho_w2 / cw2 + rho_h2 / ch2), torch.pow(inter/(union + eps), gamma) # Focal_EIouelse:return iou - (rho2 / c2 + rho_w2 / cw2 + rho_h2 / ch2) # EIouelif SIoU:# SIoU Loss https://arxiv.org/pdf/2205.12740.pdfs_cw = (b2_x1 + b2_x2 - b1_x1 - b1_x2) * 0.5 + epss_ch = (b2_y1 + b2_y2 - b1_y1 - b1_y2) * 0.5 + epssigma = torch.pow(s_cw ** 2 + s_ch ** 2, 0.5)sin_alpha_1 = torch.abs(s_cw) / sigmasin_alpha_2 = torch.abs(s_ch) / sigmathreshold = pow(2, 0.5) / 2sin_alpha = torch.where(sin_alpha_1 > threshold, sin_alpha_2, sin_alpha_1)angle_cost = torch.cos(torch.arcsin(sin_alpha) * 2 - math.pi / 2)rho_x = (s_cw / cw) ** 2rho_y = (s_ch / ch) ** 2gamma = angle_cost - 2distance_cost = 2 - torch.exp(gamma * rho_x) - torch.exp(gamma * rho_y)omiga_w = torch.abs(w1 - w2) / torch.max(w1, w2)omiga_h = torch.abs(h1 - h2) / torch.max(h1, h2)shape_cost = torch.pow(1 - torch.exp(-1 * omiga_w), 4) + torch.pow(1 - torch.exp(-1 * omiga_h), 4)if Focal:return iou - torch.pow(0.5 * (distance_cost + shape_cost) + eps, alpha), torch.pow(inter/(union + eps), gamma) # Focal_SIouelse:return iou - torch.pow(0.5 * (distance_cost + shape_cost) + eps, alpha) # SIouelif WIoU:if Focal:raise RuntimeError("WIoU do not support Focal.")elif scale:return getattr(WIoU_Scale, '_scaled_loss')(self), (1 - iou) * torch.exp((rho2 / c2)), iou # WIoU https://arxiv.org/abs/2301.10051else:return iou, torch.exp((rho2 / c2)) # WIoU v1if Focal:return iou - rho2 / c2, torch.pow(inter/(union + eps), gamma) # Focal_DIoUelse:return iou - rho2 / c2 # DIoUc_area = cw * ch + eps # convex areaif Focal:return iou - torch.pow((c_area - union) / c_area + eps, alpha), torch.pow(inter/(union + eps), gamma) # Focal_GIoU https://arxiv.org/pdf/1902.09630.pdfelse:return iou - torch.pow((c_area - union) / c_area + eps, alpha) # GIoU https://arxiv.org/pdf/1902.09630.pdfif Focal:return iou, torch.pow(inter/(union + eps), gamma) # Focal_IoUelse:return iou # IoU
相关文章:

【IoU全总结】GIoU, DIoU, CIoU, EIoUFocal, αIoU, SIoU,WIoU【基础收藏】
🥑 Welcome to Aedream同学 s blog! 🥑 并不存在效果一定优秀的IoU,需要结合自己的网络、数据集试验。 不想深究原理可直接跳转总结。文内公式均为手打,非图片,方便查看 文章目录 L1 Loss,L2Loss࿰…...

docker 安装 mysql
第一步,安装docker ,确保centos环境符合要求,有网 yum install docker -y 第二步:拉取mysql 首先可以先查询支持的mysql: search # 拉取镜像 docker pull mysql # 或者 docker pull mysql:latest # 以上两个命令是一致的&…...

Java 流程控制之 for 循环
Java语言中的for循环是一种常用的循环结构,用于重复执行一段代码,直到指定的条件不再成立。在本篇博客中,我们将深入探讨Java中的for循环,包括其语法、用法和示例。 一、for循环的基本语法 for循环的基本语法如下: …...
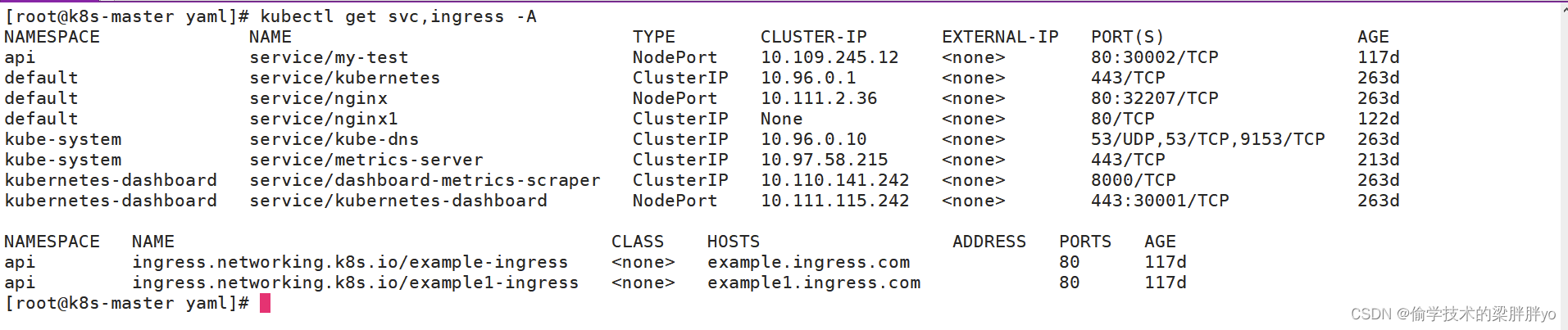
Kubernetes那点事儿——暴露服务之Ingress
Kubernetes那点事儿——暴露服务之Ingress 前言一、ingress负载均衡器Ingress Controller路由规则Ingress 二、Ingress Controller三、案例 前言 在 k8s 集群中,如果我们将服务暴露出来,提供访问,可以使用Nodeport方式,但是Nodepo…...
八股文总结
文章目录 项目介绍1.不动产项目项目难点机器学习算法调研图像提取算法调研数据集-ImageNetXceptionVGGInceptionDensenetMobilenet 系统流程图 2.图书项目技术栈ShiroMybatisMyBatis:Mybatis Plus: 面试问题 Java基础基本数据类型反射接口和抽象类异常代理模式1. 静态代理2. 动…...
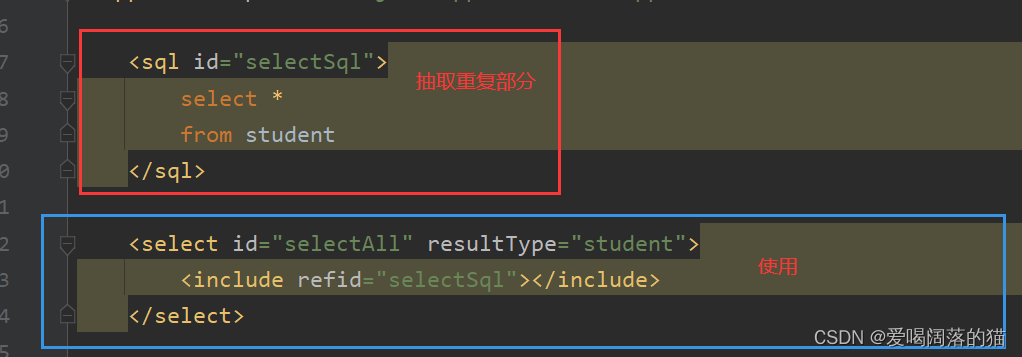
【浅学 MyBatis 】
MyBatis 笔记记录 一、MyBatis基础1. MyBatis介绍及快速入门2. 相关API介绍2.1 Resources2.2 SqlSessionFactory&&SqlSessionFactoryBuilder2.3 SqlSession 3. 映射配置文件4. 核心配置文件4.1 规范写法4.2 参数和返回类型_起别名 5. 引入Log4j 二、MyBatis进阶1. 接口…...
Windows版Redis安装
最近电脑重装了系统,很多常用的软件、应用都没有了,所以需要重新装,所以想借此机会把一些安装比较复杂的应用的安装过程,重新记录一下,方便后续, 安装 Redis默认只有Linux的版本,但是微软为了更…...

Flume面试题二十道
什么是Apache Flume? 参考答案:Apache Flume是一个可靠、分布式、可扩展的日志收集和聚合系统。它用于将大量的日志数据从不同的源(如Web服务器、应用程序日志)传输到目标(如Hadoop、HBase)中进行存储和分析…...

单链表OJ题:LeetCode--138.复制带随即指针的链表
朋友们、伙计们,我们又见面了,本期来给大家解读一下LeetCode中第138道单链表OJ题,如果看完之后对你有一定的启发,那么请留下你的三连,祝大家心想事成! 数据结构与算法专栏:数据结构与算法 个 人…...

Chapter7: SpringBoot与数据访问
尚硅谷SpringBoot顶尖教程 1. JDBC 1.1 依赖及配置 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-jdbc</artifactId> </dependency> <dependency><groupId>mysql</groupId…...

【Sqlite3】maraidb和sqlite3部分命令操作区别
maraidb和sqlite3部分命令操作区别记录 1.安装sqlite3 在实现我的视频点播系统项目时,我尝试封装了两种数据库的调用逻辑 mysql(maraidb)sqlite3 这里封装sqlite3的原因是,sqlite3主要针对的就是嵌入式数据库,其性能…...

Linux中新建用户使用sudo问题
文章目录 sudo问题 sudo问题 sudo:权限提示指令,当使用sudo这条指令时,会将普通用户的权限提升为root权限 但是在命令行新建用户,这个用户使用sudo指令对一条指令提权是用不了的 这个用户没有在sudoers file这个文件中ÿ…...
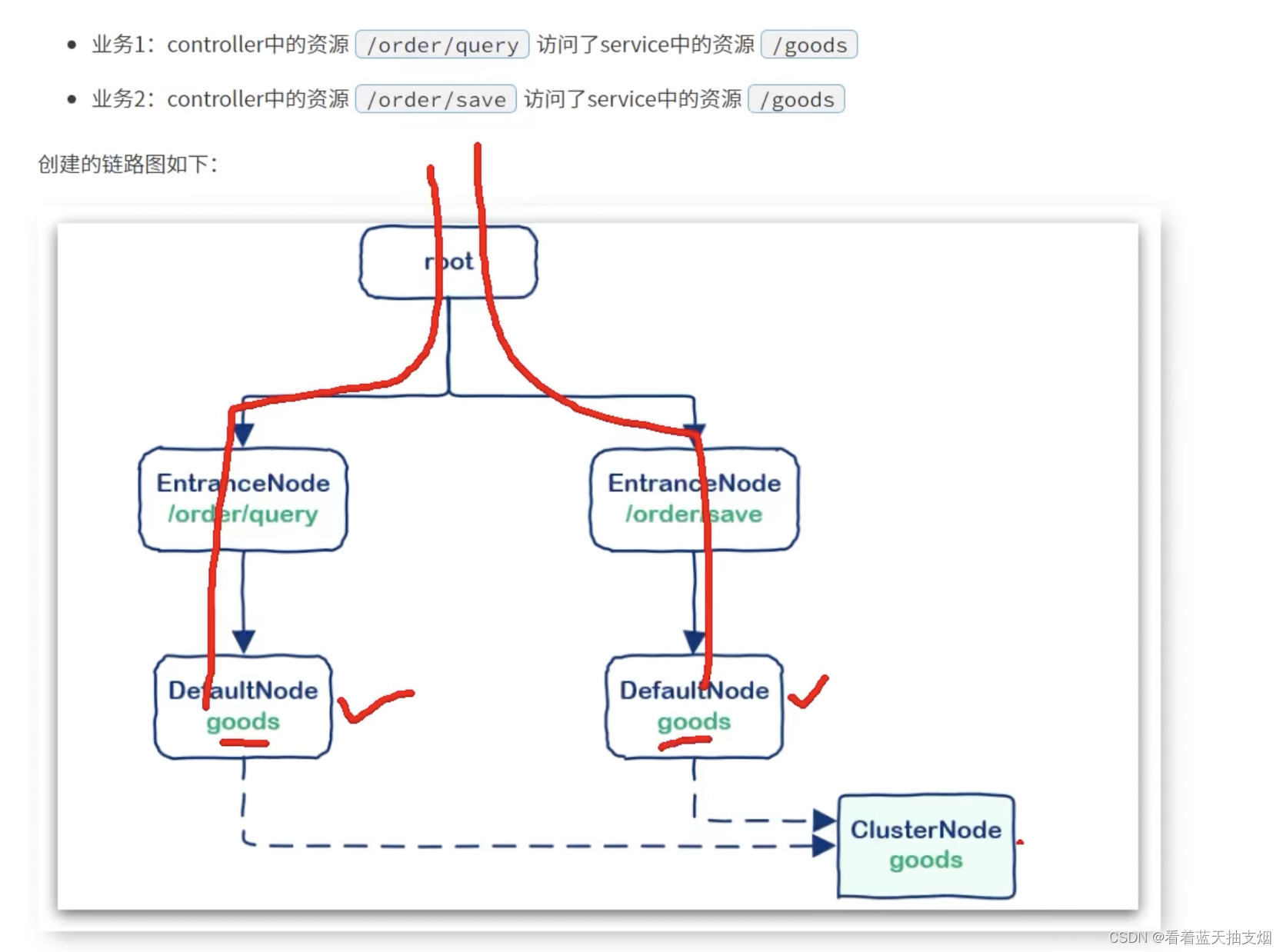
Sentinel源码分析-ProceesorSlotChain调用链及树状资源节点
Sentinel 实现流控,隔离,降级等功能,本质要做两件事: 数据统计: 统计某个资源的访问数据(QPS,RT(响应时间),异常比例)等信息规则判断: 判断流控规…...

springboot 连接 kafka集群(kafka版本 2.13-3.4.0)
springboot 连接 kafka集群 一、环境搭建1.1 springboot 环境1.2 kafka 依赖 二、 kafka 配置类2.1 发布者2.1.1 配置2.1.2 构建发布者类2.1.3 发布消息 2.2 消费者2.2.1 配置2.2.2 构建消费者类2.2.3 进行消息消费 一、环境搭建 1.1 springboot 环境 JDK 11 Maven 3.8.x spr…...
Nacos配置中心使用(Spring Cloud版)
目标 向项目中集成Nacos配置。原项目是一个SpringBoot项目。这里假设我们无法修改原有项目的SpringBoot版本。 注意 在不动SpringBoot版本的前提下,根据SpringBoot的版本,确定Spring Cloud和Nacos版本。Nacos版本其实就是Spring Cloud Alibaba版本。在…...
STM32F407硬件I2C实现MPU6050通讯(CUBEIDE)
STM32F407硬件I2C实现MPU6050通讯 文章目录 STM32F407硬件I2C实现MPU6050通讯cubeide设置写操作与读操作函数实现复位,读取温度,角度等函数封装mpu6050.cmpu6050.h代码分析 DMP移植1.修改头文件路径为自己的头文件路径2.修改I2C读写函数为自己mcu平台的读…...
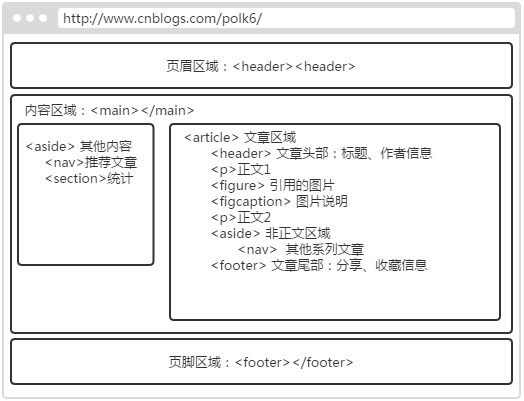
HTML5 语义元素(一)页面结构
本篇主要介绍HTML5增加的语义元素中关于页面结构方面的,包含: <article>、<aside>、<figure>、<figcaption>、<footer>、<header>、<main>、<nav>、<section>等元素。 目录 1. 语义元素介绍 1.…...
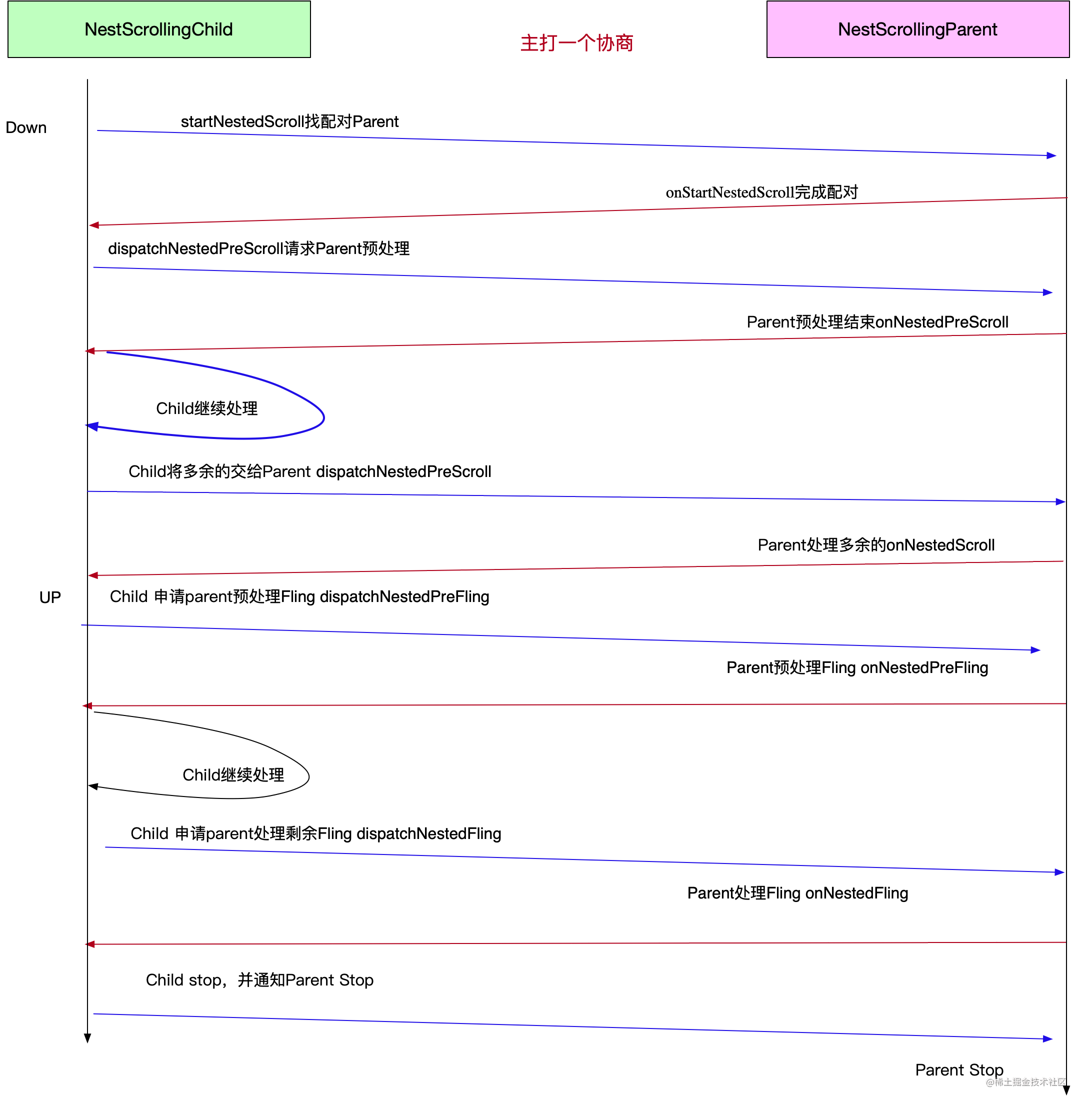
嵌套滚动实践:onInterceptTouchEvent与NestedScrolling【实用为准】
嵌套滚动:内外两层均可滚动,比如上半部分是一个有限的列表,下半部分是WebView,在内层上半部分展示到底的时候,外部父布局整体滚动内部View,将底部WevView拉起来,滚动到顶部之后再将滚动交给内部…...
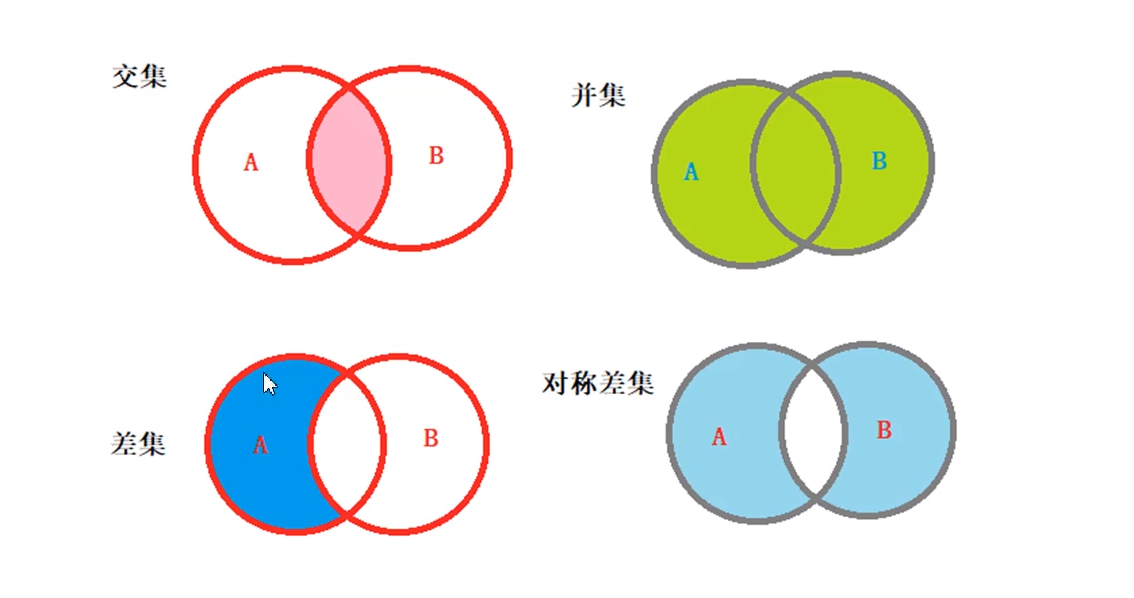
Redis入门 - 5种基本数据类型
原文首更地址,阅读效果更佳! Redis入门 - 5种基本数据类型 | CoderMast编程桅杆https://www.codermast.com/database/redis/five-base-datatype.html 说明 在我们平常的业务中基本只会使用到Redis的基本数据类型(String、List、Hash、Set、…...
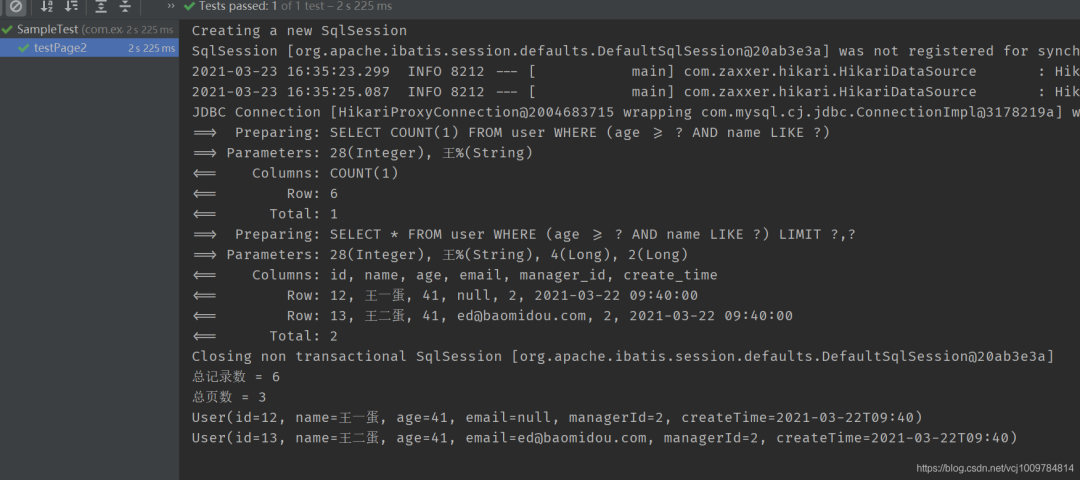
mybatis-plus用法(一)
MyBatis-plus 是一款 Mybatis 增强工具,用于简化开发,提高效率。下文使用缩写 mp来简化表示 MyBatis-plus,本文主要介绍 mp 整合 Spring Boot 的使用。 (5条消息) mybatis-plus用法(二)_渣娃工程师的博客-CSDN博客 1…...

如何快速上手League Akari:英雄联盟智能助手完全指南
如何快速上手League Akari:英雄联盟智能助手完全指南 【免费下载链接】League-Toolkit 兴趣使然的、简单易用的英雄联盟工具集。支持战绩查询、自动秒选等功能。基于 LCU API。 项目地址: https://gitcode.com/gh_mirrors/le/League-Toolkit League Akari是一…...

Bidili Generator零基础入门:5分钟搭建SDXL图片生成工具
Bidili Generator零基础入门:5分钟搭建SDXL图片生成工具 1. 引言:从零开始,5分钟拥有你的AI画师 想象一下,你只需要输入一段文字描述,就能在几分钟内得到一张细节丰富、风格独特的精美图片。无论是为你的社交媒体创作…...

2026 降重 / AIGC 率终极横评:9 大 AI 工具,从 “99.8% AI 痕” 到 “合规绿灯” 的毕业通关秘籍
前言:AI 检测时代,毕业生的 “双率噩梦” 正在升级 2026 年毕业季,毕业论文的 “生死线” 早已不止是重复率 —— 知网、维普、格子达等平台相继上线 AIGC 检测模块,“AI 生成痕迹疑似度 99.8%” 成为比查重不过更致命的扣分点。…...

Qwen3.5-35B-AWQ-4bit图片问答效果对比:单图多问 vs 换图重问的上下文管理实测
Qwen3.5-35B-AWQ-4bit图片问答效果对比:单图多问 vs 换图重问的上下文管理实测 你是不是也遇到过这样的困惑:用AI模型分析图片时,上传一张图,问了几个问题,然后换一张新图再问,结果AI的回答好像还停留在上…...
:追踪predict()耗时、内存泄漏、特征漂移——仅开放72小时下载)
【限时开源】R 4.5部署监控仪表盘(Prometheus+Grafana+Rcpp实时指标采集):追踪predict()耗时、内存泄漏、特征漂移——仅开放72小时下载
第一章:R 4.5机器学习模型部署监控体系概览在 R 4.5 环境下,机器学习模型部署后的可观测性不再仅依赖日志轮转或手动采样,而需构建覆盖数据输入、预测服务、资源状态与业务指标的多维监控闭环。该体系以 prometheus 为指标中枢,通…...
)
GME多模态向量-Qwen2-VL-2B多场景:支持视频关键帧+ASR文本联合向量建模(扩展方向)
GME多模态向量-Qwen2-VL-2B多场景:支持视频关键帧ASR文本联合向量建模 1. 模型简介与核心价值 GME多模态向量-Qwen2-VL-2B是一个强大的多模态向量生成模型,它能够处理文本、图像以及图文对等多种输入类型,并生成统一的向量表示。这个模型的…...

3大核心策略:彻底解决Gigabyte主板风扇失控难题的优化指南
3大核心策略:彻底解决Gigabyte主板风扇失控难题的优化指南 【免费下载链接】FanControl.Releases This is the release repository for Fan Control, a highly customizable fan controlling software for Windows. 项目地址: https://gitcode.com/GitHub_Trendin…...

如何解决Windows系统AirPods功能缺失问题?AirPodsDesktop全方位增强方案实测
如何解决Windows系统AirPods功能缺失问题?AirPodsDesktop全方位增强方案实测 【免费下载链接】AirPodsDesktop ☄️ AirPods desktop user experience enhancement program, for Windows and Linux (WIP) 项目地址: https://gitcode.com/gh_mirrors/ai/AirPodsDes…...

Mirage Flow在STM32嵌入式开发中的应用:边缘AI解决方案
Mirage Flow在STM32嵌入式开发中的应用:边缘AI解决方案 在嵌入式设备上实现AI推理一直是开发者面临的挑战,尤其是像STM32这样的资源受限平台。传统方案要么性能不足,要么功耗太高,很难在边缘设备上实现实用的AI功能。 Mirage Fl…...

空地协同智能消防系统:多智能体嵌入式工程实践
1. 项目概述2023年全国大学生电子设计竞赛G题“空地协同智能消防系统”是一项面向复杂动态环境的多智能体协同控制工程实践任务。该系统由四旋翼无人机与地面消防车构成闭环协作单元,需在40dm48dm矩形场域内完成全覆盖路径规划、火源识别定位、空地信息同步、自主灭…...
