哈希表--day1--基本理论介绍
文章目录
- 哈希表
- 哈希函数
- 哈希碰撞
- 拉链法
- 线性探测法
- 常见的三种哈希函数
- 数组
- set
- map
- 总结
哈希表
Hash table是根据关键码的值来直接进行访问的数据结构。
其实直白来讲其实数组就是一张哈希表,不过其索引是十分简单的,我们通过0来访问num[0],就是通过索引进行访问,得到对应的数据。
而对于个人理解,哈希表一般都是用来快速判断一个元素是否出现集合里。而涉及到Hash table 就需要了解Hash function。
哈希函数
哈希函数,把学生的姓名直接映射为哈希表上的索引,然后就可以通过查询索引下标快速知道这位同学是否在这所学校里了。
哈希函数实际上就是通过hashCode把名字转化为数值,一般hashcode是通过特定编码方式,可以将其他数据格式转化为不同的数值,然后根据哈希表对应的数组大小,将这个数值%定义的数组的大小,得到的数值就是学生名字映射为哈希表上的索引数字,从而访问数组当中的各个元素。
但是这样子避免不了会出现不同的名字对应相同的映射的索引数字,比如小张和小李都经过哈希函数运算得到1,对应访问的都是数组下的num[1]这一个元素,那该如何去确定到底是该访问小张对应的数据还是小李对应的数据,这就出现了一个矛盾,这就是对应的哈希矛盾或者哈希碰撞。
哈希碰撞
一般来说哈希碰撞有俩种方法进行解决:拉链法或者线性探测法
拉链法
拉链法实际上就是在对应数据域的地方,将其变成链表元素,然后将对应索引数值相同的数据都保存到这个虚拟头节点之后。然后再次进行别的编码函数判断,求得对应的是元素的索引值。
举个例子:校长和小李对应都是索引值为1,那么我们将num[1]定义为头节点,后面串上小张和小李对应的数据,用单链表对应串起来,然后再访问的时候,再根据小张还是小李,再次进行判断,即可。
其实拉链法就是要选择适当的哈希表的大小,这样既不会因为数组空值而浪费大量内存,也不会因为链表太长而在查找上浪费太多时间。
线性探测法
使用线性探测法,一定要保证tableSize大于dataSize。 我们需要依靠哈希表中的空位来解决碰撞问题。
例如冲突的位置,放了小李,那么就向下找一个空位放置小王的信息。所以要求tableSize一定要大于dataSize ,要不然哈希表上就没有空置的位置来存放 冲突的数据了。
其实关于哈希碰撞还有非常多的细节,感兴趣的同学可以再好好研究一下,这里我就不再赘述了。
常见的三种哈希函数
当我们想使用哈希法来解决问题的时候,我们一般会选择如下三种数据结构。
数组
set (集合)
map(映射)
数组
这里数组就没啥可说的了,占个坑。。。。
set
在C++中,set提供以下三种数据结构,其底层实现以及优劣如下表所示:
| 集合 | 底层实现 | 是否有序 | 数值是否可以重复 | 能否修改数值 | 查询效率 | 增删效率 |
|---|---|---|---|---|---|---|
| std::set | 红黑树 | 有序 | 否 | 否 | O(log n) | O(log n) |
| std::multiset | 红黑树 | 有序 | 是 | 否 | O(logn) | O(logn) |
| std::unordered_set | 哈希表 | 无序 | 否 | 否 | O(1) | O(1) |
std::unordered_set底层实现为哈希表,std::set 和std::multiset 的底层实现是红黑树,红黑树是一种平衡二叉搜索树,所以key值是有序的,但key不可以修改,改动key值会导致整棵树的错乱,所以只能删除和增加。
map
| 映射 | 底层实现 | 是否有序 | 数值是否可以重复 | 能否更改数值 | 查询效率 | 增删效率 |
|---|---|---|---|---|---|---|
| std::map | 红黑树 | key有序 | key不可重复 | key不可修改 | O(logn) | O(logn) |
| std::multimap | 红黑树 | key有序 | key可重复 | key不可修改 | O(log n) | O(log n) |
| std::unordered_map | 哈希表 | key无序 | key不可重复 | key不可修改 | O(1) | O(1) |
std::unordered_map 底层实现为哈希表,std::map 和std::multimap 的底层实现是红黑树。同理,std::map 和std::multimap 的key也是有序的。
当我们要使用集合来解决哈希问题的时候,优先使用unordered_set,因为它的查询和增删效率是最优的,如果需要集合是有序的,那么就用set,如果要求不仅有序还要有重复数据的话,那么就用multiset。
那么再来看一下map ,在map 是一个key-value 的数据结构,map中,对key是有限制,对value没有限制的,因为key的存储方式使用红黑树实现的。
虽然std::set、std::multiset 的底层实现是红黑树,不是哈希表,std::set、std::multiset 使用红黑树来索引和存储,不过给我们的使用方式,还是哈希法的使用方式,即key和value。所以使用这些数据结构来解决映射问题的方法,我们依然称之为哈希法。 map也是一样的道理。
这里在说一下,一些C++的经典书籍上 例如STL源码剖析,说到了hash_set hash_map,这个与unordered_set,unordered_map又有什么关系呢?
实际上功能都是一样一样的,但是unordered_set在C++11的时候被引入标准库了,而hash_set并没有,所以建议还是使用unordered_set比较好,这就好比一个是官方认证的,hash_set,hash_map 是C++11标准之前民间高手自发造的轮子。
总结
总结一下,当我们遇到了要快速判断一个元素是否出现集合里的时候,就要考虑哈希法。
但是哈希法也是牺牲了空间换取了时间,因为我们要使用额外的数组,set或者是map来存放数据,才能实现快速的查找。
相关文章:

哈希表--day1--基本理论介绍
文章目录 哈希表哈希函数哈希碰撞拉链法线性探测法 常见的三种哈希函数数组setmap 总结 哈希表 Hash table是根据关键码的值来直接进行访问的数据结构。 其实直白来讲其实数组就是一张哈希表,不过其索引是十分简单的,我们通过0来访问num[0],…...
基于OpenMV的疲劳驾驶检测系统的设计
一、前言 借助平台将毕业设计记录下来,方便以后查看以及与各位大佬朋友们交流学习。如有问题可以私信哦。 本文主要从两个方面介绍毕业设计:硬件,软件(算法)。以及对最后的实验结果进行分析。感兴趣的朋友们可以评论区…...

chatgpt赋能python:使用Python来寻找两个列表不同元素的方法
使用Python来寻找两个列表不同元素的方法 在编写Python程序时,我们经常需要比较两个列表的元素,找出它们之间的不同之处。在搜索引擎优化(SEO)方面,这种比较对于找出两个网站内容的差异也非常有用。在这篇文章中&…...
简单学生管理系统
简单学生管理系统(Java)_封奚泽优的博客-CSDN博客https://blog.csdn.net/weixin_64066303/article/details/130667107?spm1001.2014.3001.5501 转载请注明出处,尊重作者劳动成果。 目录 前期准备: 数据库的连接: 用户账号类:…...
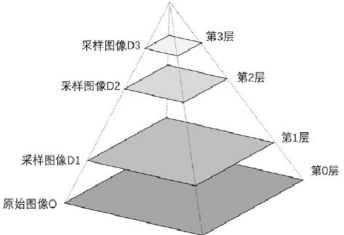
图像金字塔
图像金字塔是由一幅图像的多个不同分辨率的子图构成的图像集合。是通过一个图像不断的降低采样率产生的,最小的图像可能仅仅有一个像素点。下图是一个图像金子塔的示例。从图中可以看到,图像金字塔是一系列以金字塔形状排列的、自底向上分辨率逐渐降低…...

Springboot整合Camunda工作流引擎实现审批流程实例
环境:Spingboot2.6.14 camunda-spring-boot-starter7.18.0 环境配置 依赖配置 <camunda.version>7.18.0</camunda.version> <dependency><groupId>org.camunda.bpm.springboot</groupId><artifactId>camunda-bpm-spring-boo…...
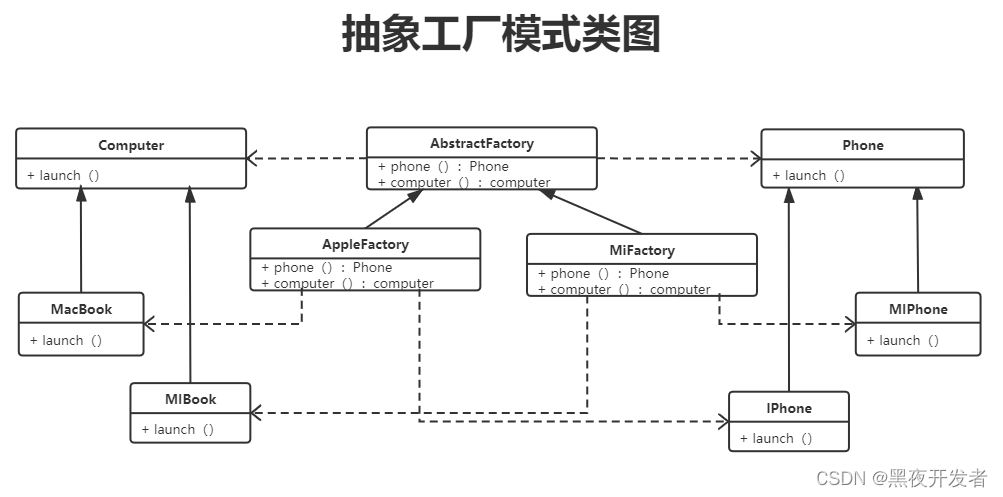
PHP设计模式21-工厂模式的讲解及应用
文章目录 前言基础知识简单工厂模式工厂方法模式抽象工厂模式 详解工厂模式普通的实现更加优雅的实现 总结 前言 本文已收录于PHP全栈系列专栏:PHP快速入门与实战 学会好设计模式,能够对我们的技术水平得到非常大的提升。同时也会让我们的代码写的非常…...

【玩转Docker小鲸鱼叭】理解Docker的核心概念
Docker核心概念 Docker有三大核心概念:镜像(Image)、容器(Container)、仓库(Repository) 1、镜像(Image) Docker镜像 是我们创建和运行Docker容器的基础,它…...

Eureka 心跳和服务续约源码探秘——图解、源码级解析
🍊 Java学习:社区快速通道 🍊 深入浅出RocketMQ设计思想:深入浅出RocketMQ设计思想 🍊 绝对不一样的职场干货:大厂最佳实践经验指南 📆 最近更新:2023年5月25日 🍊 点赞 👍 收藏 ⭐留言 📝 都是我最大的动力! 文章目录 分布式系统的心跳机制心跳机制的实…...

代码随想录二刷 530 二叉搜索树的最小绝对差 98. 验证二叉搜索树 700. 二叉搜索树中的搜索
530 二叉搜索树的最小绝对差 代码如下 func getMinimumDifference(root *TreeNode) int { var pre *TreeNode res : math.MaxInt var traverse func(root * TreeNode) traverse func(root * TreeNode) { if root nil { return } traverse(root.Left) …...
Docker安装——CentOS7.6(详细版)
ps:docker官网 在 CentOS 上安装 Docker 引擎 |官方文档 () 一、确定版本(必须是7以上版本) cat /etc/redhat-release 二、卸载旧版本(或者之前装过,没有安装过就不用管了) (root用…...
)
论信息系统项目的整体管理(范文)
论信息系统项目的整体管理(范文) 【摘要】 2016年10月,XX省卫生健康委启动了XX省分级转诊服务平台建设项目,我在项目中担任项目经理,负责项目的全面管理工作。该平台作为全省上下级医院转诊的信息化通道,…...

【音视频处理】音频编码AAC详解,低码率提高音质?
大家好,欢迎来到停止重构的频道。 本期我们介绍音频编码格式AAC。 AAC是音频最常用的编码格式之一,几乎所有的播放器都支持这个编码格式。 其他音频编码格式都是类似的,只是某些细节存在差别,如压缩算法、某些音频参数存在限制…...

逆函数学习
逆函数 给定关系 R ⊆ X Y R\subseteq X\times Y R⊆XY,颠倒 R R R的所有有序偶可以得到 R R R的逆关系 R ~ ⊆ Y X \tilde{R}\subseteq Y\times X R~⊆YX 但是对于函数 f : X → Y f:X\to Y f:X→Y而言,其逆关系 f ~ \tilde{f} f~可能不是 Y Y Y到…...

代码审计——SSRF详解
为方便您的阅读,可点击下方蓝色字体,进行跳转↓↓↓ 01 漏洞描述02 审计要点03 漏洞特征04 漏洞案例05 修复方案 01 漏洞描述 服务端请求伪造攻击(SSRF)也成为跨站点端口攻击,是由于一些应用在向第三方主机请求资源时提…...
搭建Scala开发环境
一、Windows上安装Scala 1、到Scala官网下载Scala Scala2.13.10下载网址:https://www.scala-lang.org/download/2.13.10.html 单击【scala-2.13.10.msi】超链接,将scala安装程序下载到本地 2、安装Scala 双击安装程序图标,进入安装向导&…...
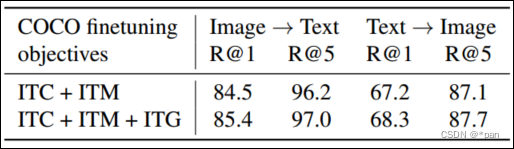
BLIP和BLIP2
文章主要是对BLIP2 (使用冻结图像编码器和大型语言模型的Bootstrapping语言图像预训练)论文的阅读笔记,也对BLIP(用于统一视觉语言理解和生成的Bootstrapping语言图像预训练)算法进行了简单的介绍。 文章:…...

微信小程序开发实战 ⑨(TabBar)
作者 : SYFStrive 博客首页 : HomePage 📜: 微信小程序 📌:个人社区(欢迎大佬们加入) 👉:社区链接🔗 📌:觉得文章不错可以点点关注 Ǵ…...
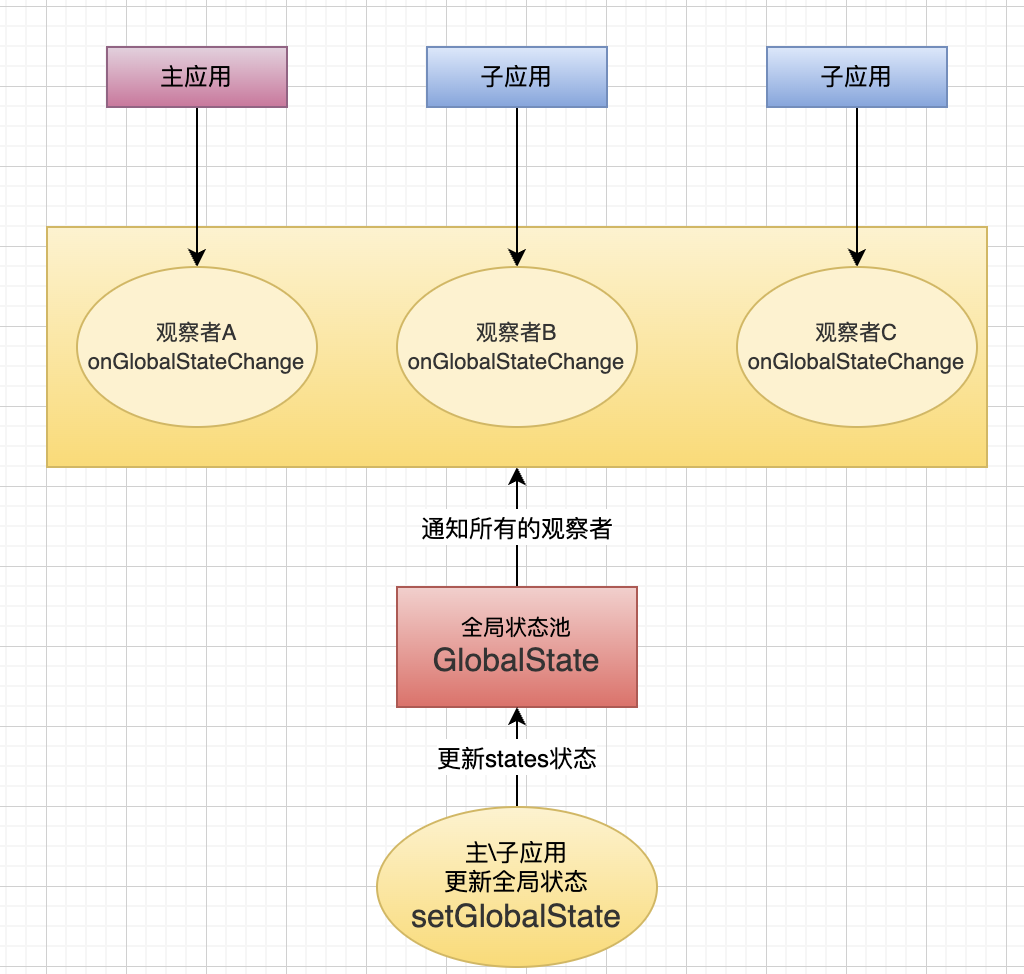
微前端探秘:初始微前端、现有方案和未来趋势
初识微前端 微前端是什么 概念: 微前端是指存在于浏览器中的微服务。 微前端是一种类似于微服务的架构,它将微服务的理念应用于浏览器端,即将单页面前端应用由单一的单体应用转变为把多个小型前端应用聚合为一体的应用。这就意味着前端应用…...

运维(SRE)成长之路-第2天 文本编辑工具之神VIM
vi和vim简介 在Linux中我们经常编辑修改文本文件,即由ASCII, Unicode 或其它编码的纯文字的文件。之前介绍过nano,实际工作中我们会使用更为专业,功能强大的工具 文本编辑种类: 全屏编辑器:nano(字符工具…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...
