【数据结构】特殊矩阵的压缩存储
🎇【数据结构】特殊矩阵的压缩存储🎇

文章目录
- 🎇【数据结构】特殊矩阵的压缩存储🎇
- 🍰一.数组的存储结构
- 🚀1.数组的定义
- 🚀2.数组的存储结构
- 🍰二.特殊矩阵的存储结构
- 🚀1.普通矩阵的存储
- 🚀2.特殊矩阵的压缩存储
- 🔆1.对称矩阵
- 🔆2.三角矩阵
- 🔆3.三对角矩阵
- 🔆4.稀疏矩阵
🍰一.数组的存储结构
🚀1.数组的定义
数组是由n个相同类型的数据元素所构成的有限序列
数组和线性表的关系:
数组是线性表的推广:一维数组可以看做是一个线性表,而对于二维数组而言,可以看成是有多个线性表组成的线性表
也就是每一行 / / /列视都为一个线性表,总的线性表内每一个元素也是一个定长的线性表

🚀2.数组的存储结构
- 对于一维数组的存储,就是线性表,一维数组的所有元素在内存空间中占用一段连续的内存空间

那么,对于多维数组的存储,在计算机中是如何实现的呢?
- 对于多维数组的存储,在计算机中仍表现为一维数组的形式,也就是一段连续的内存空间

接下来,我们就要去尝试模拟计算机存放多维数组的过程:
有两种映射方式:行优先和列优先
①行优先:
以二维数组为例,以行优先存储的方式为:也就是逐行放入一维数组中

🌈 下标转换关系:
(我们默认下标从0开始)对于二维数组 A [ N ] [ M ] A[N][M] A[N][M] 中的元素 a i j a_{ij} aij ,若希望在行优先转化后的一维数组中访问它,我们可以确定其在一维数组中的下标为:
分解代码实现:
- 行优先二维转一维数组
void row_Reducedim(int a[][M],int *res, int row, int col)
{int p = 0;for (int i = 0; i < row; i++) {for (int j = 0; j < col; j++) {res[p++] = a[i][j];}}
}
- 按照索引从一维数组中取值
void visit(int res[], int i, int j)
{if (i <= N-1 && i >= 0 && j >= 0 && j <= M-1){int k = i * M + j;cout << res[k] << endl;}elsecout << "输入违规" << endl;
}
行优先完整代码实现:
#include<iostream>
using namespace std;void row_Reducedim(int a[][4],int *res, int row, int col)
{int p = 0;for (int i = 0; i < row; i++) {for (int j = 0; j < col; j++) {res[p++] = a[i][j];}}
}void Print(int a[], int n)
{for (int i = 0; i < n; i++){cout << a[i] << " ";}cout << endl;
}void visit(int res[], int i, int j)
{if (i <= 1 && i >= 0 && j >= 0 && j <= 3){int k = i * 4 + j;cout << res[k] << endl;}elsecout << "输入违规" << endl;
}int main() {int martix[2][4] ={ {1,2,3,4},{5,6,7,8} };int res[8];//二维转一维row_Reducedim(martix,res, 2, 4); //行优先cout << "行转化后的一维数组为:" << endl;Print(res,8);//二维数组元素在一维数组内的映射int i, j;cout << "对于行转换后的矩阵,输入要访问的元素在二维数组中的行,列下标数(>=0)" << endl;cin >> i >> j;visit(res, i, j);system("pause");return 0;
}
②列优先:
以二维数组为例,以行优先存储的方式为:也就是逐列放入一维数组中

🌈 下标转换关系:
对于二维数组 A [ N ] [ M ] A[N][M] A[N][M] 中的元素 a i j a_{ij} aij ,其在一维数组中的下标为:
分解代码实现:
- 列优先二维转一维数组
void col_Reducedim(int a[][4], int* res1, int row, int col)
{int p = 0;for (int j = 0; j < col; j++) {for (int i = 0; i < row; i++) {res1[p++] = a[i][j];}}
}
- 按照索引从一维数组中取值
void visit1(int res[], int i, int j)
{if (i <= 1 && i >= 0 && j >= 0 && j <= 3){int k = j * 2 + i;cout << res[k] << endl;}elsecout << "输入违规" << endl;
}
列优先完整代码实现:
#include<iostream>
using namespace std;void col_Reducedim(int a[][4], int* res1, int row, int col)
{int p = 0;for (int j = 0; j < col; j++) {for (int i = 0; i < row; i++) {res1[p++] = a[i][j];}}
}void Print(int a[], int n)
{for (int i = 0; i < n; i++){cout << a[i] << " ";}cout << endl;
}void visit1(int res[], int i, int j)
{if (i <= 1 && i >= 0 && j >= 0 && j <= 3){int k = j * 2 + i;cout << res[k] << endl;}elsecout << "输入违规" << endl;
}int main() {int martix[2][4] ={ {1,2,3,4},{5,6,7,8} };int res1[8];//二维转一维col_Reducedim(martix, res1, 2, 4); //列优先cout << "列转化后的一维数组为:" << endl;Print(res1, 8);int a, b;cout << "对于列转换后的矩阵,输入要访问的元素在二维数组中的行,列下标数(>=0)" << endl;cin >> a >> b;visit1(res1, a, b);system("pause");return 0;
}
输出结果:

🍰二.特殊矩阵的存储结构
🚀1.普通矩阵的存储
对于普通的矩阵,我们可以将其视为二维数组进行处理,也就是按行优先和列优先的方式存储,在之前也已经提到过

🚀2.特殊矩阵的压缩存储
压缩存储:指为多个值相同的元素所分配一个存储空间,对零元素不分配存储空间,用于节省空间
接下来,我们来看几个典型的特殊矩阵:
🔆1.对称矩阵
对于一个n阶的方阵,我们可以将其划分为主对角线,上三角区和下三角区,而对于对称矩阵来说,有 a i j = a j i a_{ij}=a_{ji} aij=aji,因此,若仍然采用二维数组存储,会造成一半的空间浪费
策略:
因此,我们其实只需要 存主对角线和下三角块 即可:

🌊 对称矩阵与存储后一维数组的映射关系:
我们规定矩阵元素的下标 i , j i,j i,j的范围为 [ 1 , n ] [1,n] [1,n],而一维数组的下标默认是从0开始的

- 一维数组大小:
第一行:一个元素, a 11 a_{11} a11
第二行:两个元素, a 21 , a 22 a_{21},a_{22} a21,a22
…
共有 n n n 行,则元素总数 k = n ∗ ( n + 1 ) / 2 k=n*(n+1)/2 k=n∗(n+1)/2

-
压缩存储后的访问:
又回到了,压缩完成之后,我们应该如何获取这些数据呢?
我们只需要定义一个映射函数即可:

策略:
不难发现,如果我们希望取出二维数组内的元素 a i j a_{ij} aij,我们已知了它的行号和列号:
①先看行向:
在 a i j a_{ij} aij上面的元素(即前 i − 1 i-1 i−1行)的元素个数为:
②再看列向:
在 a i j a_{ij} aij前面的元素(即前 j − 1 j-1 j−1行)的元素个数为:
由于一维数组下标是从 0 0 0开始的,因此: a i j 的一维数组下标 = 在 a i j 前的元素个数 a_{ij}的一维数组下标=在a_{ij}前的元素个数 aij的一维数组下标=在aij前的元素个数
再由 a i j = a j i a_{ij}=a_{ji} aij=aji,因此,映射函数为:

完整代码实现:
#include<iostream>
using namespace std;//打印下三角
void triangle(int a[][3], int* res, int row, int col)
{int p = 0;for (int i = 0; i < row; i++) {for (int j = 0; j < col; j++) {if (i >= j)res[p++] = a[i][j];}}
}//访问
void visit(int res[], int i, int j)
{if (i >= j){int k = i * (i - 1) / 2 + j - 1;cout << res[k] << endl;}else{int k = j * (j - 1) / 2 + i - 1;cout << res[k] << endl;}
}//打印一维数组
void Print(int a[], int n)
{for (int i = 0; i < n; i++){cout << a[i] << " ";}cout << endl;
}int main() {int martix[3][3] ={ {1,2,3},{2,1,2},{3,2,1} };int res[6];triangle(martix, res, 3, 3);cout << "下三角的一维数组为:" << endl;Print(res,6);int i, j;cout << "请输入需要访问的元素aij中的下标i,j(>=1):" << endl;cin >> i >> j;visit(res, i, j);system("pause");return 0;
}
输出结果:
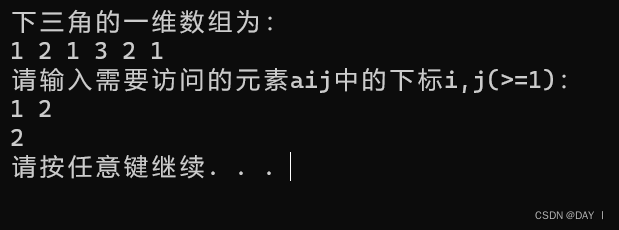
🔆2.三角矩阵
三角矩阵就是有一个三角区全为常量的矩阵

策略:
其储存思维和对称矩阵类似,不同之处就在于:
✅ 存储完下三角区和主对角线后,紧接着存储对角线上方的常量,也就是要在对称矩阵构造的一维数组后面添加一个常数项

-
一维数组的大小:
k = n ∗ ( n + 1 ) / 2 k=n*(n+1)/2 k=n∗(n+1)/2 -
映射函数为:

完整代码实现:
#include<iostream>
using namespace std;//打印下三角
void triangle(int a[][3], int* res, int row, int col,int n)
{int p = 0;for (int i = 0; i < row; i++) {for (int j = 0; j < col; j++) {if (i >= j)res[p++] = a[i][j];}}//存常量int c = a[0][n-1];res[n * (n + 1) / 2] = c;
}//访问
void visit(int res[], int i, int j,int n)
{if (i >= j){int k = i * (i - 1) / 2 + j - 1;cout << res[k] << endl;}else{int k = n * (n + 1)/2;cout << res[k] << endl;}
}//打印一维数组
void Print(int a[], int n)
{for (int i = 0; i < n; i++){cout << a[i] << " ";}cout << endl;
}int main() {int martix[3][3] ={ {1,4,4},{2,1,4},{3,2,1} };int res[6];triangle(martix, res, 3, 3,3);cout << "下三角的一维数组为:" << endl;//加一个常数项Print(res, 6+1);int i, j;cout << "请输入需要访问的元素aij中的下标i,j(>=1):" << endl;cin >> i >> j;visit(res, i, j,3);system("pause");return 0;
}
输出结果:

🔆3.三对角矩阵
三对角矩阵也称带状矩阵,对于n阶方阵的A中的任一元素 a i j a_{ij} aij,当 ∣ i − j ∣ > 1 |i-j|>1 ∣i−j∣>1时, a i j = 0 a_{ij}=0 aij=0

策略:
将三条对角线上的元素按行优先原则存放在一维数组中(零元素不存)

-
一维数组的大小:
由于只有第一行和最后一行只有两个元素,因此,一维数组大小为:
l e n = 3 n − 2 len=3n-2 len=3n−2 -
映射函数为:
由于前 i − 1 i-1 i−1行有 3 i − 1 3i-1 3i−1个元素,当前行前面有 j − i + 1 j-i+1 j−i+1个元素
k = 2 i + j − 3 k=2i+j-3 k=2i+j−3
反之,若我们已知 a i j a_{ij} aij存放于一维数组中的第 k个位置,怎么推出行数和列数呢?

i = ⌈ ( k + 2 ) / 3 ⌉ i=⌈(k+2)/3⌉ i=⌈(k+2)/3⌉ 再由公式 k = 2 i + j − 3 k=2i+j-3 k=2i+j−3可以推出: j = k − 2 i + 3 j=k-2i+3 j=k−2i+3
完整代码实现:
#include<iostream>
#include<math.h>
using namespace std;//转一维矩阵
void Three(int a[][4], int* res, int row, int col)
{int p = 0;for (int i = 0; i < row; i++) {for (int j = 0; j < col; j++) {if (a[i][j] != 0)res[p++] = a[i][j];}}
}void Print(int a[],int n) {for (int i = 0; i < n; i++) {cout << a[i] << " ";}cout << endl;
}void visit1(int a[], int i, int j)
{int k = 2*i + j - 3;printf("a%d%d=%d\n", i,j,a[k]);
}void visit2(int a[], int k)
{int i, j;i = ceil((k + 2) / 3);j = k - 2 * i + 3;printf("访问的元素为:a%d%d\n", i, j);
}int main() {int martix[4][4] ={{1,2,0,0},{1,2,3,0},{0,2,3,4},{0,0,3,4}};int res[10];//转一维Three(martix, res, 4, 4);cout << "三对角的一维矩阵为:" << endl;Print(res, 10);//正向访问int i, j;cout << "请输入需要访问的元素aij中的下标i,j(>=1):" << endl;cin >> i >> j;visit1(res, i, j);//反向访问int k;cout<<"请输入该元素在一维数组中的下标:" << endl;cin >> k;visit2(res, k);system("pause");return 0;
}
输出结果:

🔆4.稀疏矩阵
还有一种特殊矩阵,其矩阵内的非0元素远远少于零元素,则称其为稀疏矩阵
e . g e.g e.g 如下矩阵:

| 我们只存取非零元素,但其分布往往没有规律,因此,我们还应该记录它的位置 |
策略:
将非零元素的行,列,值构成一个三元组 (行标,列标,值) (行标,列标,值) (行标,列标,值)
✅ 我们用结构体定义这个三元组:
#define Maxsize 100//结构体定义三元组
typedef struct {int i;int j;int val;
}Triple[Maxsize]; //结构体数组

完整代码实现:
#include<iostream>
#define Maxsize 100
using namespace std;//结构体定义三元组
typedef struct {int i;int j;int val;
}Triple[Maxsize]; //结构体数组//稀疏矩阵转三元组
void triple(Triple &T,int a[][5],int row,int col,int &p)
{for (int i = 0; i < row; i++) {for (int j = 0; j < col; j++) {if (a[i][j] != 0) {T[p].i = i+1;T[p].j = j+1;T[p].val = a[i][j];p++;}}}
}void Print(Triple &T,int len) {for (int i = 0; i < len; i++) {printf("a%d%d=",T[i].i,T[i].j);cout << T[i].i<< " " << T[i].j << " " << T[i].val << endl;}
}int main() {int martix[5][5] ={{0,2,0,0,0},{0,0,1,0,2},{3,0,0,0,1},{0,5,0,0,0},{1,0,4,0,0}};Triple T;int p = 0;//稀疏矩阵转三元组triple(T, martix, 5, 5, p);cout << "转化后的三元组为(矩阵元素下标从1开始):\n" << endl;Print(T, p);system("pause");return 0;
}
输出结果:



相关文章:

【数据结构】特殊矩阵的压缩存储
🎇【数据结构】特殊矩阵的压缩存储🎇 🌈 自在飞花轻似梦,无边丝雨细如愁 🌈 🌟 正式开始学习数据结构啦~此专栏作为学习过程中的记录🌟 文章目录 🎇【数据结构】特殊矩阵的压缩存储Ἰ…...

在layui中使用vue,使用vue进行页面数据部分数据更新
layui是一款非常优秀的框架,使用也非常的广泛,许多后台管理系统都使用layui,简单便捷,但是在涉及页面部分数据变化,就比较难以处理,比如一个页面一个提交页,提交之后部分数据实时进行更新&#…...

Vue中如何进行数据导入与Excel导入
Vue中如何进行数据导入与Excel导入 Vue是一款非常流行的JavaScript框架,它提供了一套用于构建用户界面的工具和库。在Vue中,我们可以使用多种方式来导入数据,包括从服务器获取数据、从本地存储获取数据、从文件中读取数据等等。其中…...

git 的基本操作
1. git建立本地仓库 在想要建立的目录下输入命令 git init 我们可以看一下 .git目录下有什么 2. 配置git本地仓库 配置用户的 name 和 email 命令:git config [...] 配置完后,我们像查看一下 刚才的配置 2.1 查看配置命令 git config -l 2.2 删除…...
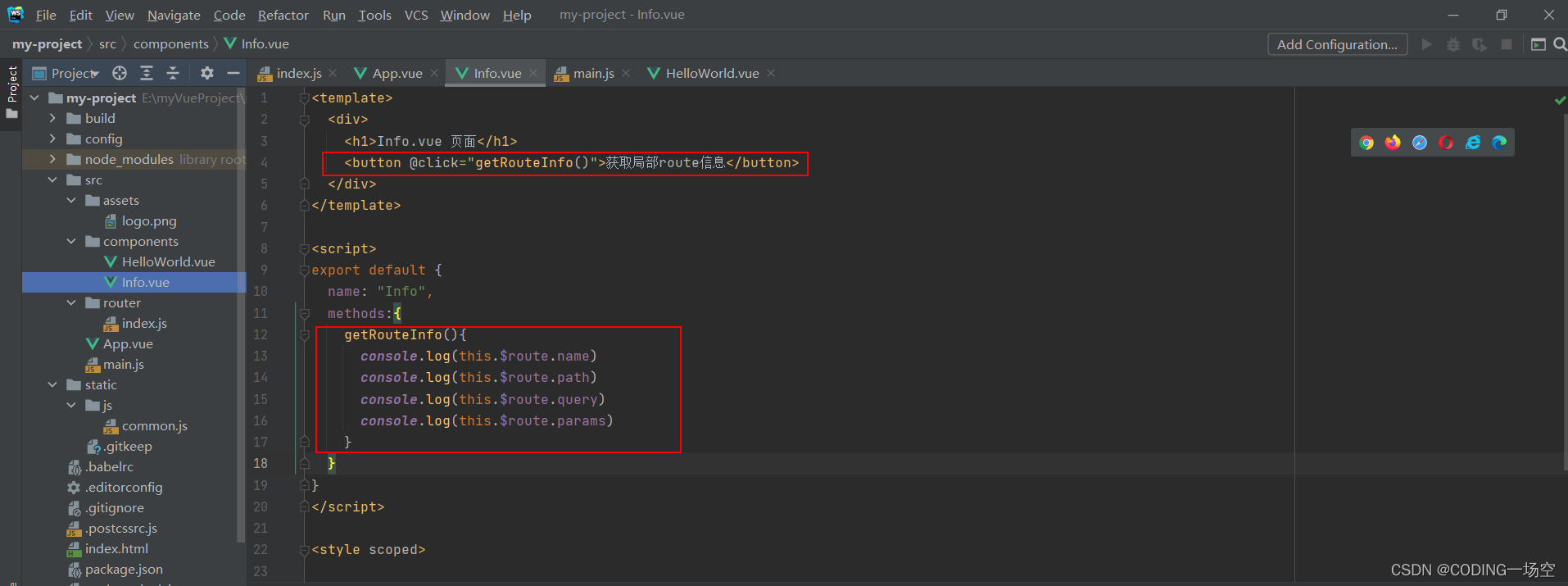
搭建Vue项目以及项目的常见知识
前言:使用脚手架搭建vue项目,使用脚手架可以开发者能够开箱即用快速地进行应用开发而开发。 搭建 #创建一个基于 webpack 模板的新项目 vue init webpack my-project #选择所需要的选项如图: cd my-project npm run dev访问localhost:808…...

TypeScript ~ TS Webpack构建工具 ⑦
作者 : SYFStrive 博客首页 : HomePage 📜: TypeScript ~ TS 📌:个人社区(欢迎大佬们加入) 👉:社区链接🔗 📌:觉得文章不错可以点点关注 &…...

Rust 自建HTTP Server支持图片响应
本博客是在杨旭老师的 rust web 全栈教程项目基础上进行修改,支持了图片资源返回,杨旭老师的rust web链接如下: https://www.bilibili.com/video/BV1RP4y1G7KFp1&vd_source8595fbbf160cc11a0cc07cadacf22951 本人默认读者已经学习了相关…...

[游戏开发][Unity]UnityWebRequest使用大全
首先记录个小问题 使用new UnityWebRequest的方式,最终的downloadHandler是个null 使用UnityWebRequest.Get的方式,最终的downloadHandler会是DownloadHandlerBuffer 从网站或本地下载内容,包括文本或二进制数据 IEnumerator downloadfile(st…...
如何使用Fiddler对手机进行弱网测试?(干货教程)
1.首先,fiddler连接手机 1)Tools->Options->Connections->设置端口8888,勾选Allow remote computers to connect 2)配置手机 注:手机和电脑需要在同一局域网下 手机进入网络详情,将代理改为手动 设置主机名、端口 主机…...

专业科普:什么是单片机?
一、什么是单片机 单片机诞生于20世纪70年代末,它是指一个集成在一块芯片上的完整计算机系统。单片机具有一个完整计算机所需要的大部分部件:CPU、内存、内部和外部总线系统,目前大部分还会具有外存。同时集成诸如通讯接口、定时器ÿ…...

深度学习-第T11周——优化器对比实验
深度学习-第T11周——优化器对比实验 深度学习-第T11周——优化器对比实验一、前言二、我的环境三、前期工作1、导入数据集2、查看图片数目3、查看数据 四、数据预处理1、 加载数据1、设置图片格式2、划分训练集3、划分验证集4、查看标签 2、数据可视化3、检查数据4、配置数据集…...
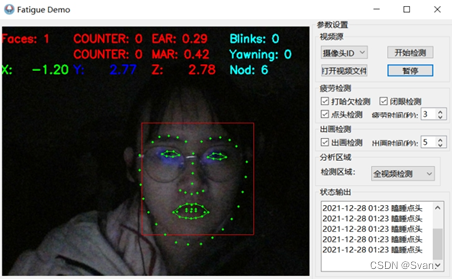
基于Dlib的疲劳检测系统
需要源码的朋友可以私信我 基于Dlib的疲劳检测系统 1、设计背景及要求2、系统分析3、系统设计3.1功能结构图3.2基于EAR、MAR和HPE算法的疲劳检测3.2.1基于EAR算法的眨眼检测3.2.2基于MAR算法的哈欠检测3.3.3基于HPE算法的点头检测 4、系统实现与调试4.1初步实现4.2具体实现过程…...

three.js通过CubeTexture加载环境贴图,和RGBELoader加载器加载hdr环境贴图
一、使用CubeTexture进行环境贴图 1.CubeTexture使用介绍 Three.js中可以通过使用CubeTexture进行环境贴图,CubeTexture需要将6张图片(正面、反面、上下左右)包装成一个立方体纹理。下面是一个简单的例子: 首先需要加载六张贴图…...
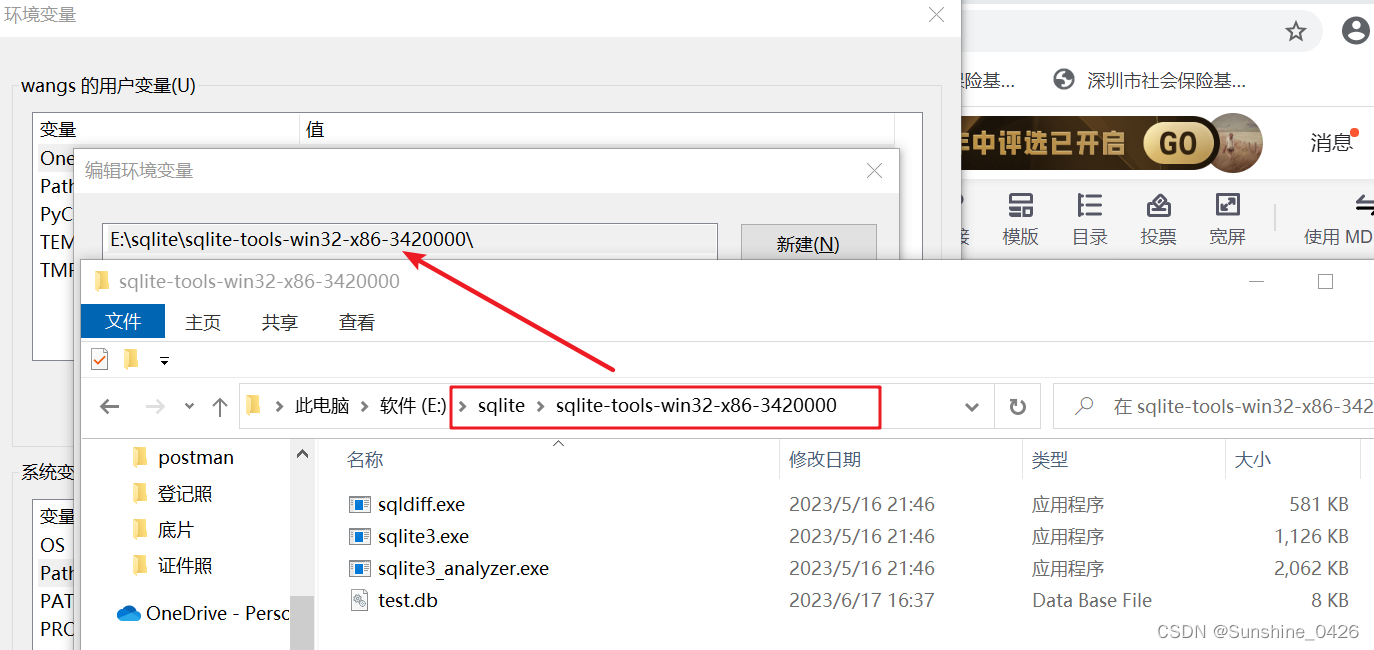
pycharm中Terminal输入sqlite3,出现无法将sqlite项识别为cmdlet**的解决方法
前提:本机上已安装sqlite3,安装详见:pycharm社区版中安装配置sqlite3_Sunshine_0426的博客-CSDN博客 问题: cmd命令行中或pycharm中Terminal行输入sqlite3 db.sqlite3命令后,出现“无法将“sqlite3”项识别为 cmdlet…...
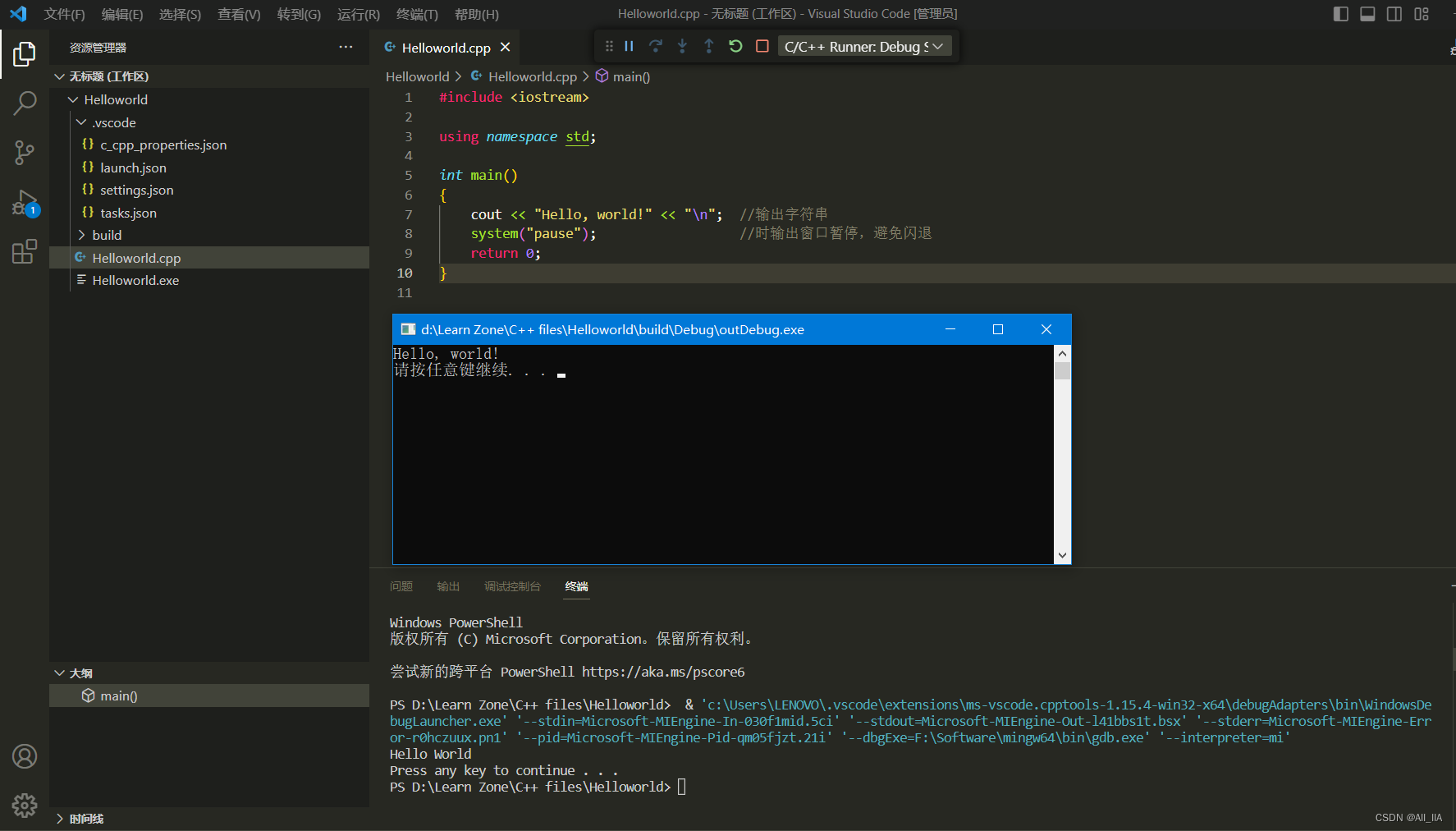
VSCode 安装配置教程详解包含c++环境配置方法
vscode安装教程及c环境配置详解 vscode下载安装下载C扩展插件VScode C环境配置配置环境变量检查 MinGW 安装配置编译器:配置构建任务检查是否安装了编译器配置完毕 vscode下载安装 地址:官网下载地址 直接打开下载好的.exe文件进行安装即可࿰…...
)
Baumer工业相机堡盟工业相机如何通过BGAPISDK将图像放大缩小显示(C#)
Baumer工业相机堡盟工业相机如何通过BGAPISDK将图像放大缩小显示(C#) Baumer工业相机Baumer工业相机BGAPISDK和图像放大缩小的技术背景Baumer工业相机通过BGAPISDK将相机图像图像放大缩小功能1.引用合适的类文件2.通过BGAPISDK将相机图像图像放大缩小功能…...

8.1 PowerBI系列之DAX函数专题-进阶-解决列排序对计算的影响
需求 下列矩阵中,在月份列不按照原始数据的month_no排列时,能正确计算销售额占比,但是当月份按照month_no排序时就会出错,需要解决这个问题。 实现 month % divide([amount],calculate([amount],all(date[month desc]))) //排…...
Java的第十二篇文章——集合
目录 第十二章 集合 学习目标 1. 集合框架的由来 2. 集合框架的继承体系 3. Collection接口 3.1 Collection接口的常用方法 4. Iterator接口 4.1 Iterator接口的抽象方法 4.2 获取迭代器接口实现类 4.3 迭代器的实现原理 4.4 并发修改异常 4.5 集合存储自定义对象并…...

docker 镜像制作 与 CI/CD
目录 镜像到底是什么? 使用docker创建镜像 步骤: 1、编辑Dockerfile(Dockerfile是docker制作镜像的配方文件) 2、编辑requirements.txt文件 3、编辑app.py文件,我们的程序文件 4、生成镜像文件 5、查看生成的镜…...
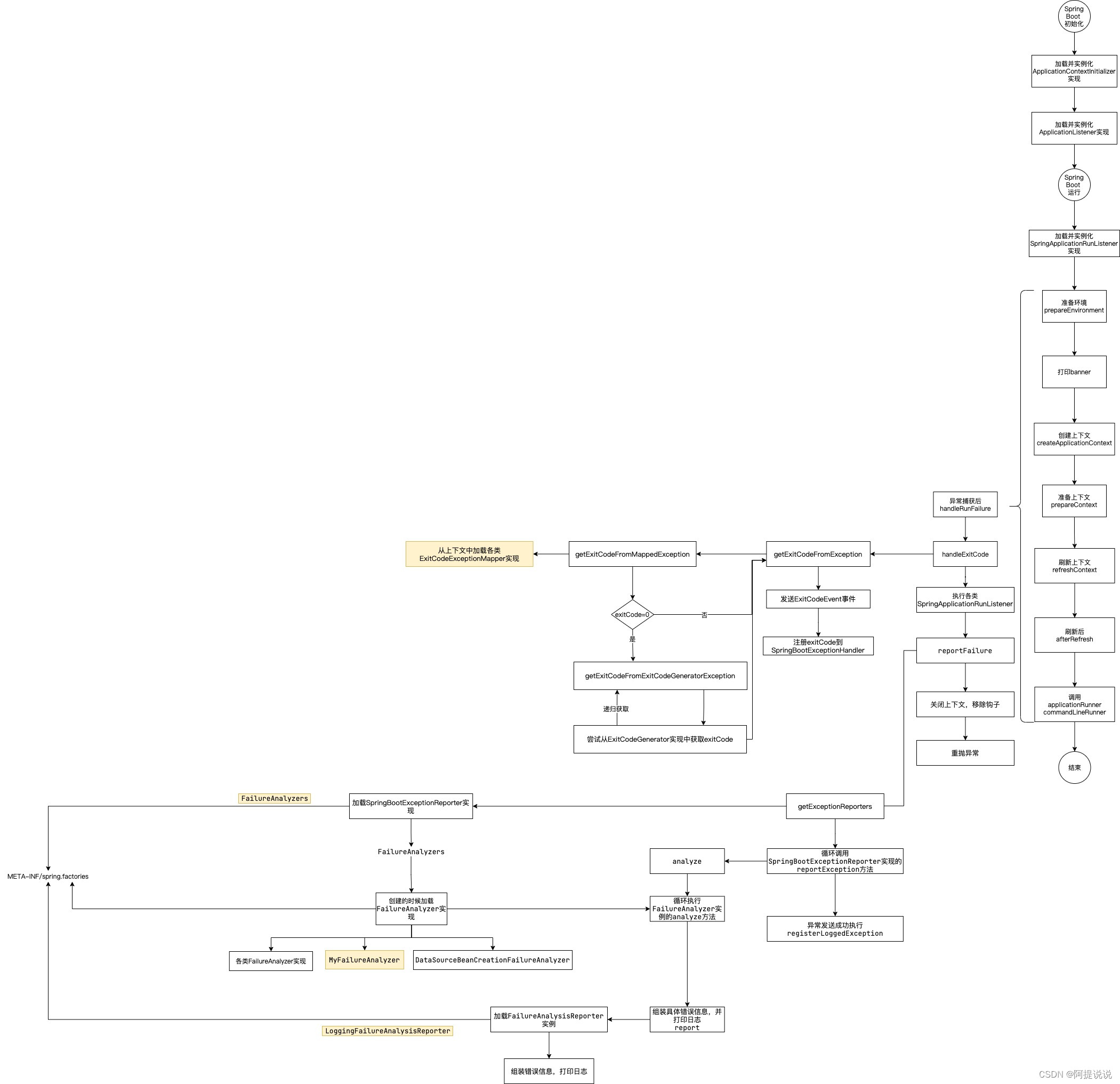
Spring Boot 异常报告器解析
基于Spring Boot 3.1.0 系列文章 Spring Boot 源码阅读初始化环境搭建Spring Boot 框架整体启动流程详解Spring Boot 系统初始化器详解Spring Boot 监听器详解Spring Boot banner详解Spring Boot 属性配置解析Spring Boot 属性加载原理解析Spring Boot 异常报告器解析 创建自定…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...

【 java 虚拟机知识 第一篇 】
目录 1.内存模型 1.1.JVM内存模型的介绍 1.2.堆和栈的区别 1.3.栈的存储细节 1.4.堆的部分 1.5.程序计数器的作用 1.6.方法区的内容 1.7.字符串池 1.8.引用类型 1.9.内存泄漏与内存溢出 1.10.会出现内存溢出的结构 1.内存模型 1.1.JVM内存模型的介绍 内存模型主要分…...

ubuntu22.04有线网络无法连接,图标也没了
今天突然无法有线网络无法连接任何设备,并且图标都没了 错误案例 往上一顿搜索,试了很多博客都不行,比如 Ubuntu22.04右上角网络图标消失 最后解决的办法 下载网卡驱动,重新安装 操作步骤 查看自己网卡的型号 lspci | gre…...

智能职业发展系统:AI驱动的职业规划平台技术解析
智能职业发展系统:AI驱动的职业规划平台技术解析 引言:数字时代的职业革命 在当今瞬息万变的就业市场中,传统的职业规划方法已无法满足个人和企业的需求。据统计,全球每年有超过2亿人面临职业转型困境,而企业也因此遭…...

图解JavaScript原型:原型链及其分析 | JavaScript图解
忽略该图的细节(如内存地址值没有用二进制) 以下是对该图进一步的理解和总结 1. JS 对象概念的辨析 对象是什么:保存在堆中一块区域,同时在栈中有一块区域保存其在堆中的地址(也就是我们通常说的该变量指向谁&…...

深入解析光敏传感技术:嵌入式仿真平台如何重塑电子工程教学
一、光敏传感技术的物理本质与系统级实现挑战 光敏电阻作为经典的光电传感器件,其工作原理根植于半导体材料的光电导效应。当入射光子能量超过材料带隙宽度时,价带电子受激发跃迁至导带,形成电子-空穴对,导致材料电导率显著提升。…...
qt+vs Generated File下的moc_和ui_文件丢失导致 error LNK2001
qt 5.9.7 vs2013 qt add-in 2.3.2 起因是添加一个新的控件类,直接把源文件拖进VS的项目里,然后VS卡住十秒,然后编译就报一堆 error LNK2001 一看项目的Generated Files下的moc_和ui_文件丢失了一部分,导致编译的时候找不到了。因…...
