查找的基本概念
查找表是由同一类型的数据元素(或记录)构成的集合。
根据给定的某个值,在查找表中确定一个其关键字等于给定值的数据元素或记录。
关键字:用来标识一个数据元素(或记录)的某个数据项的值。
查找算法的评价指标:关键字的平均比较次数,也称平均查找长度。
线性表的查找:
顺序查找
应用范围:顺序表或线性链表表示的静态查找表;表内元素之间无序。
优点:算法简单,逻辑次序无要求
缺点:ASL太长,时间效率太低
折半查找(二分)
每次将待查记录所在区间缩小一半。
优点:效率比顺序查找高。
缺点:只适用于有序表,且限于顺序存储结构。
分块查找(索引顺序查找)
查找效率:ASL=Lb+Lw(对索引表查找的ASL+对块内查找的ASL)
数表的查找:
二叉排序树
平衡二叉树(左<根<右)
散列表的查找:
基本思想:记录的存储位置与关键字之间存在对应关系
对应关系---hash函数
优点:查找效率高,O(1)
缺点:空间效率低
散列方法(杂凑法):选取某个函数时,依该函数按关键字计算元素的存储位置,并按此存放;查找时,由同一个函数对给定值k计算地址,将k与地址单元中元素关键码进行比,确定查找是否成功。
散列函数:散列方法中使用的转换函数
冲突:不同的关键码映射到同一个散列地址
同义词:具有相同函数值的多个关键字
构造散列函数考虑的因素:
执行速度
关键字的长度
散列表的大小
关键字的分布情况
查找频率
构造方法:
直接定址法:
优点:以关键码key的某个线性函数值为散列地址,不会产生冲突
缺点:要占用连续地址空间,空间效率低
除留余数法:hash(key)=key mod p(p是一个整数)
处理冲突的方法:
开放定址法:
基本思想:有冲突时就去寻找下一个空的散列地址
常用:
线性探测法
二次探测法
链地址法
基本思想:相同散列地址的记录链成一单链表
优点:非同义词不会冲突,无“聚集”现象,链表上结点空间动态申请,更适合于表长不确定的情况
散列表技术具有很好的平均性能,优于一些传统的技术。
链地址法优于开地址法。
除留余数法作散列函数优于其他类型函数。
相关文章:

查找的基本概念
查找表是由同一类型的数据元素(或记录)构成的集合。根据给定的某个值,在查找表中确定一个其关键字等于给定值的数据元素或记录。关键字:用来标识一个数据元素(或记录)的某个数据项的值。查找算法的评价指标…...

安装v-router出错
一、场景 1、安装v-router npm i --save vue-router 2、报错: npm ERR! code ERESOLVE npm ERR! ERESOLVE unable to resolve dependency tree npm ERR! npm ERR! While resolving: sph20.1.0 npm ERR! Found: vue2.7.14 npm ERR! node_modules/vue npm ERR! v…...

2023美赛C题:预测 Wordle 结果
以下内容全部来自本人人工翻译,仅供参考。 文章目录背景要求附件数据文件条目描述纽约时报网站上发布的Wordle指导方针词汇表参考文献服务背景 Wordle是目前纽约时报每天提供的一种受欢迎的谜题。玩家试图通过在六次或更少的机会内猜测一个五个字母的单词来解决谜题…...

minio public桶禁止在直接访问桶位置时列出所有文件url
minio的public桶因为没有限制,所以在直接访问到桶地址的时候会列出桶内所有文件的url,这样很不安全,如何禁止这个功能,可以使用三种方法 1、如果是新版的可以直接设置桶的Access Policy为自定义就好 编辑custom的Policyÿ…...

Python 元组简介
Python 的元组与列表类似,不同之处在于元组的元素不能修改。元组使用小括号,列表使用方括号。元组创建很简单,只需要在括号中添加元素,并使用逗号隔开即可。如下实例:实例(Python 2.0)tup1 (physics, chemistry, 1997…...
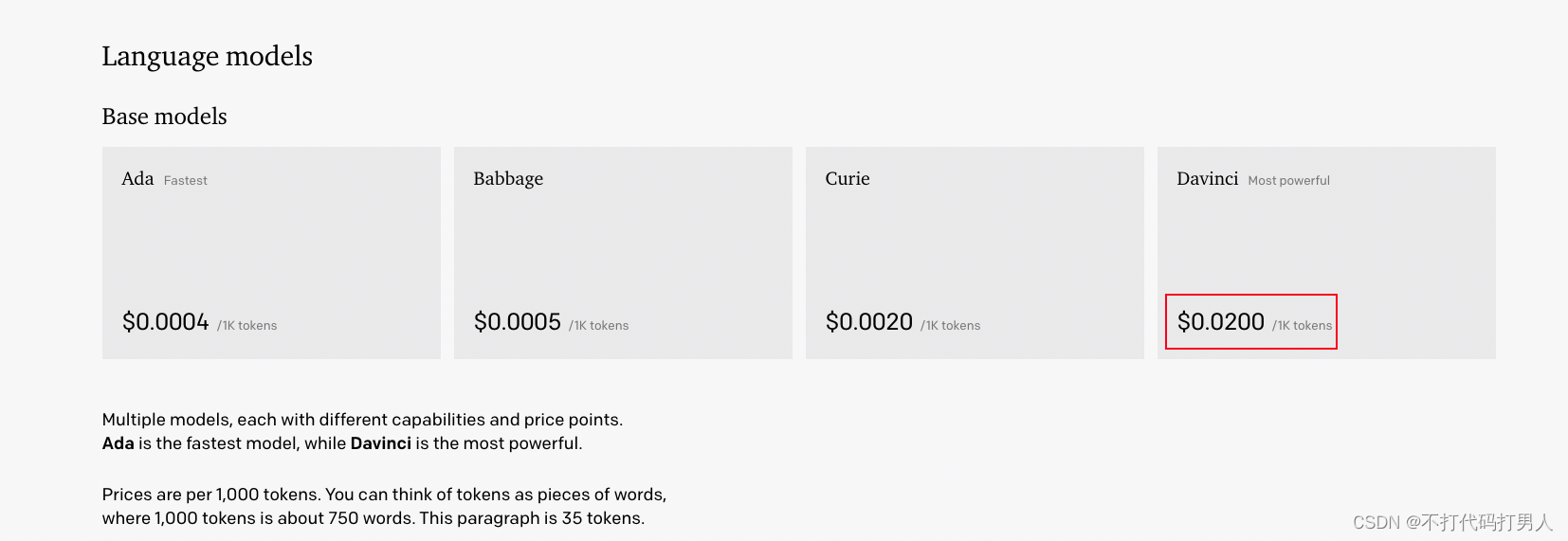
python gui构造openai api可视化页面
背景:最近chatgpt很火,前几天也想注册体验一下,一顿操作之后,卡在该国家不支持。最后发现自己的代理开在香港,改在漂亮国就行了。虽然有chatgpt可以用,但是小平是自己封装了一个,我不能输。正好…...
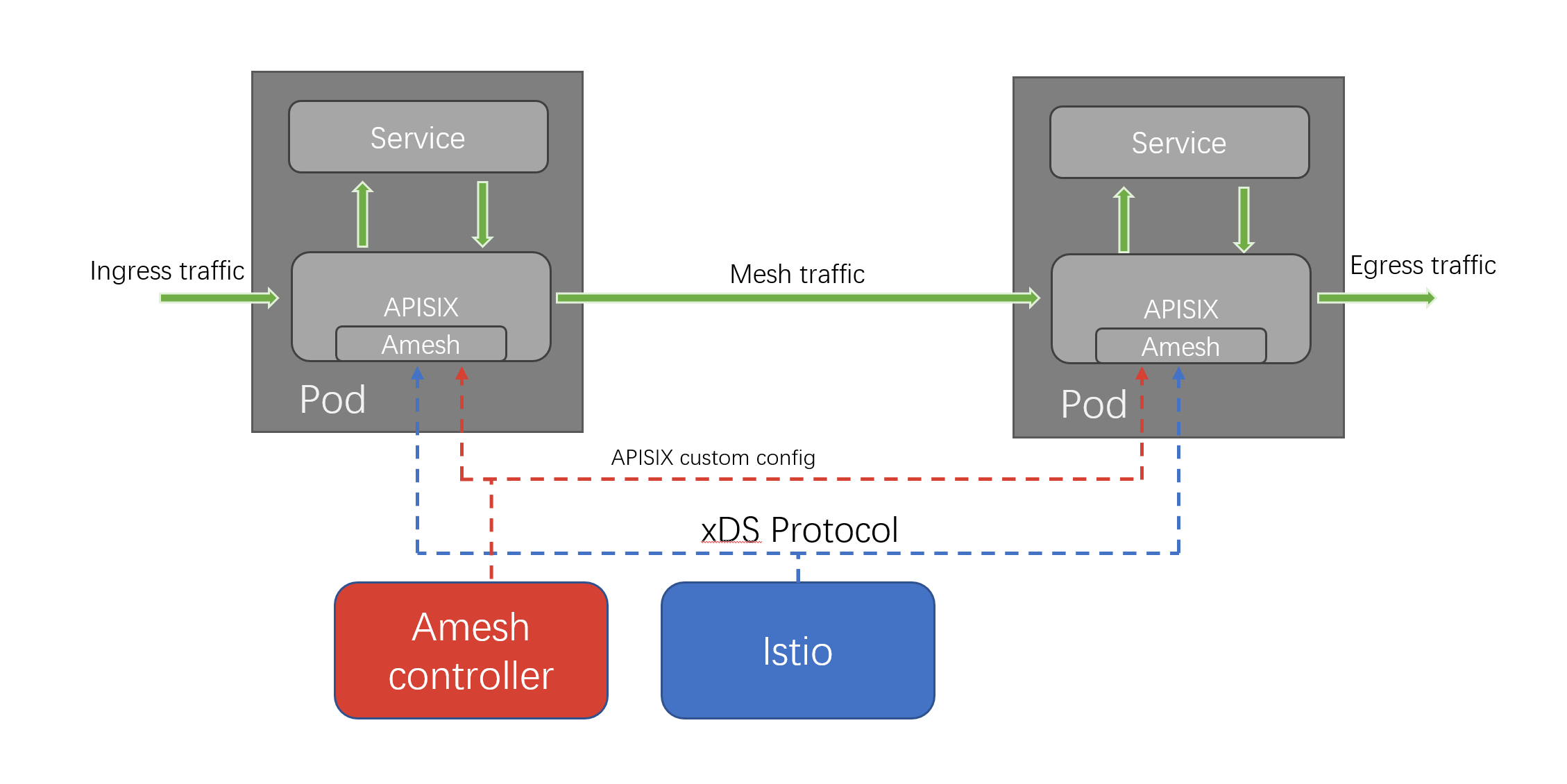
服务网格领域的百花齐放,是否存在一个更优解?
作者 lingsamuel,API7.ai 云原生技术专家,Apache APISIX Committer。作者 林志煌,API7.ai 技术工程师,Apache APISIX contributor。 服务网格是一种技术架构,它用于管理微服务系统中各个服务之间的通信,旨…...
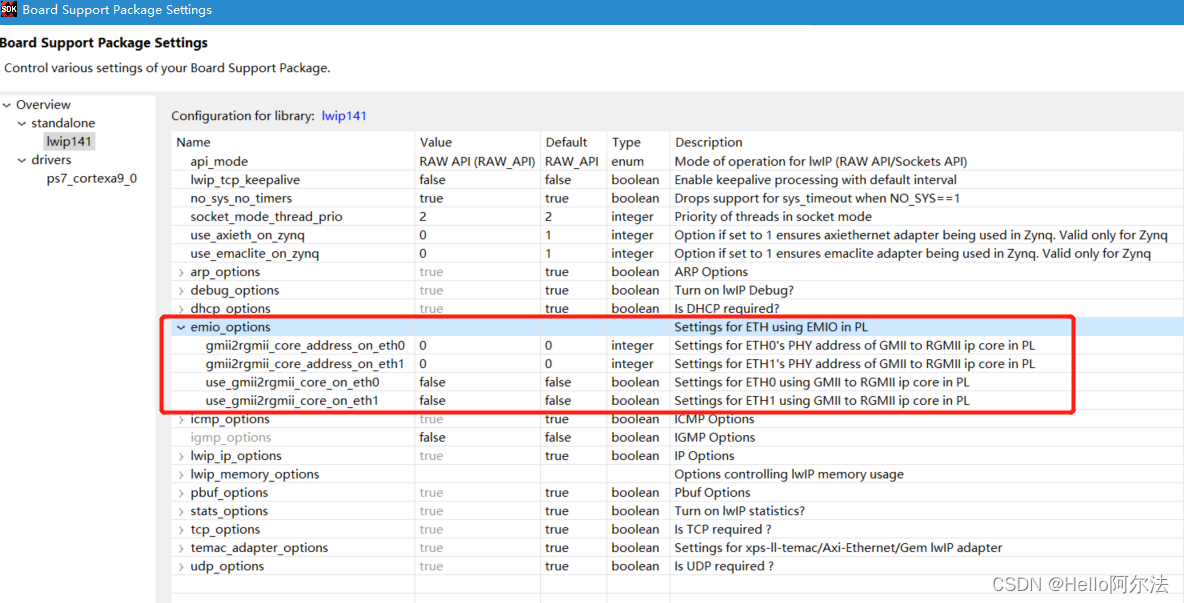
Zynq 裸机 PS + PL 双网口实现之 lwip 库文件修改
基于 xilinx vivado 2017.4 库文件 lwip141_v2_0 的修改: 添加对 PHY 芯片 ksz9031 的支持; 添加 SDK 中 LWIP 参数设置对话框 emio_options 选项; 添加 XPAR_GMII2RGMIICON_0N_ETH0_ADDR 和 XPAR_GMII2RGMIICON_0N_ETH1_ADDR 宏配置&#…...
金三银四丨黑蛋老师带你剖析-CTF岗
作者丨黑蛋二进制是个庞大的方向,对应着许许多多方向的岗位,除了之前说过的逆向岗位,漏洞岗位,病毒岗位,还有专门打CTF的岗位,CTF是网络安全领域的一种比赛。普遍来讲,大学生学习网络安全都会参…...
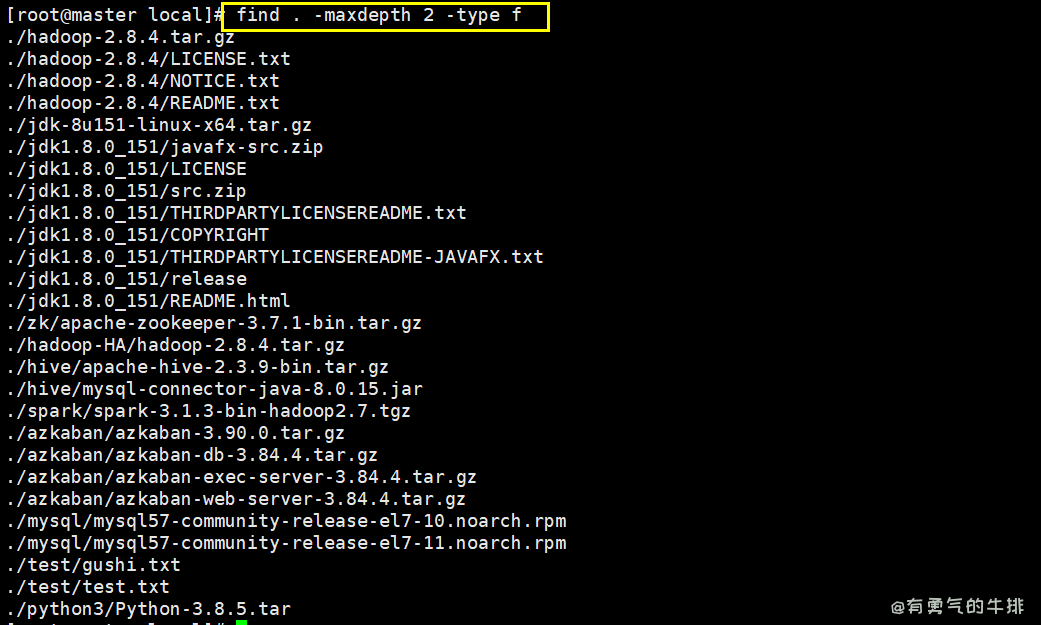
Linux find命令
哈喽,大家好,我是有勇气的牛排(全网同名)🐮 有问题的小伙伴欢迎在文末评论,点赞、收藏是对我最大的支持!!!。 1 介绍 find命令用来查找置顶目录下的文件。任何位于参数…...
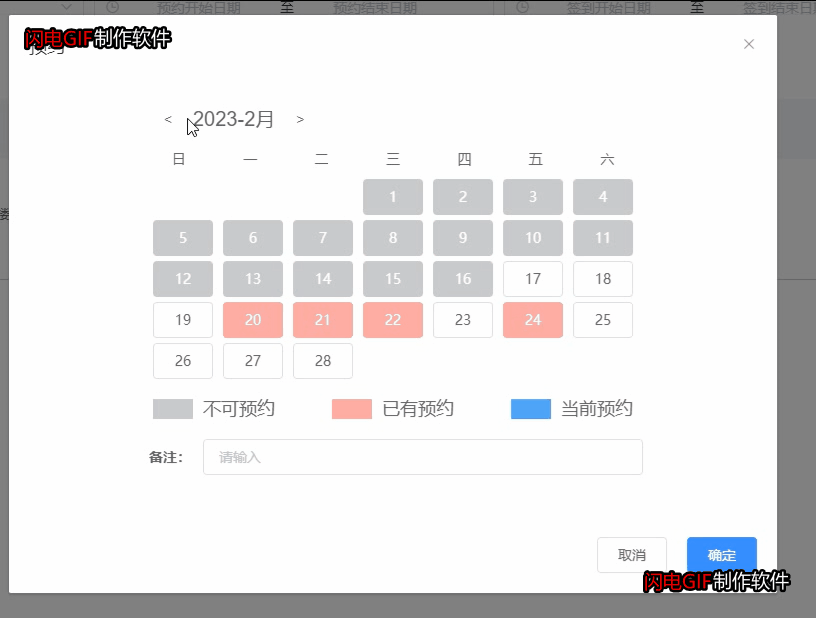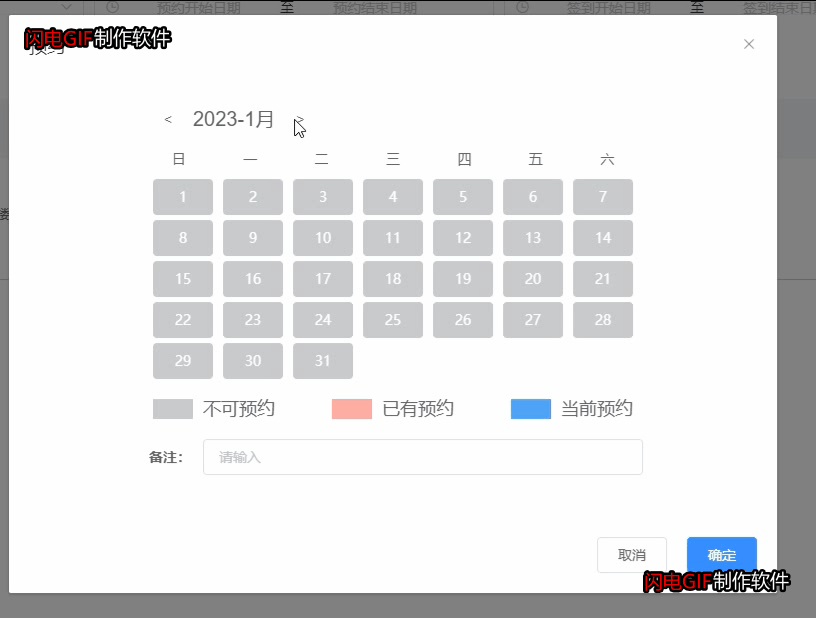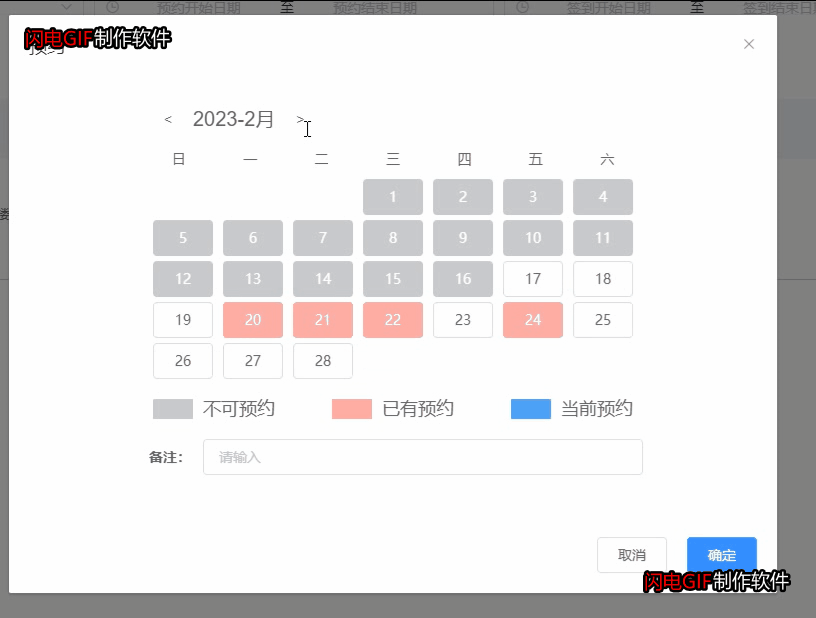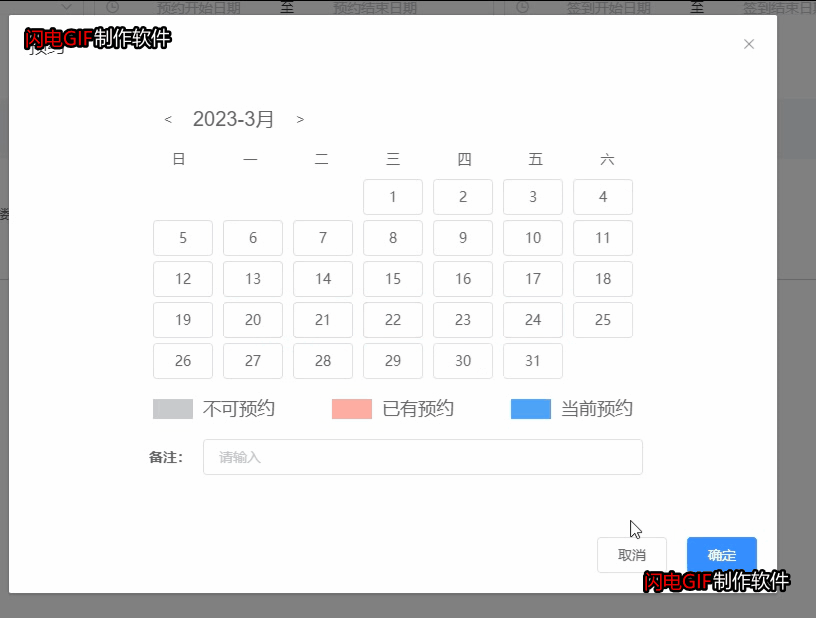
vue项目实现会议预约(包含某天的某个时间段和某月的某几天)
一、一天的时间段预约 会议预约有以下操作: 1.点击预约按钮,弹窗最近一周的预约时间点(半小时一个点),预约时间为5:00到24:00; 2.超过当前时间的时间点不允许再预约,已经预约的时间不允许再预约,…...

javacv桌面推送 通过推送和拉取udp组播视频流实现
ffmpeg udp 推流拉流命令单播推流E:/工具/ffmpeg/ffmpeg -f gdigrab -r 23 -i desktop -pkt_size 1316 -vcodec libx264 -preset:v ultrafast -tune:v zerolatency -f h264 udp://192.168.1.20:5001拉流ffplay -f h264 udp://192.168.1.20:5001 -fflags nobuffer -nofind_strea…...
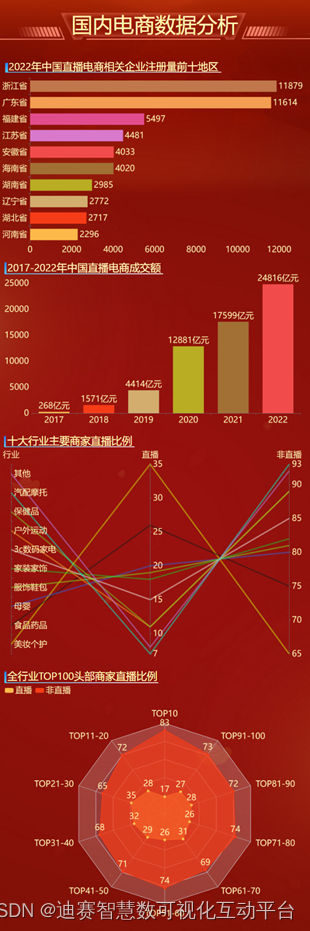
2022年直播电商成交额,更是达到了24816亿元的成交额
近年来移动网络覆盖率、网速提升,直播行业不在是陌生的行业,直播也诞生了繁多的领域,游戏直播、户外直播等,当然还有今天的主题“直播带货”。直播带货是线上销售模式的一种,由衷是为了更好的把商品展示给用户观看&…...

【学习总结】2023寒假总结
写在前面时光匆匆,白驹过隙,转眼间寒假就过去了,这次寒假可以算的上是最长的一次假期,经历了从疫情到放开,从患病到阳康,在现实与虚幻的世界中玩耍,在痛苦的数据结构中徘徊,在每次早…...
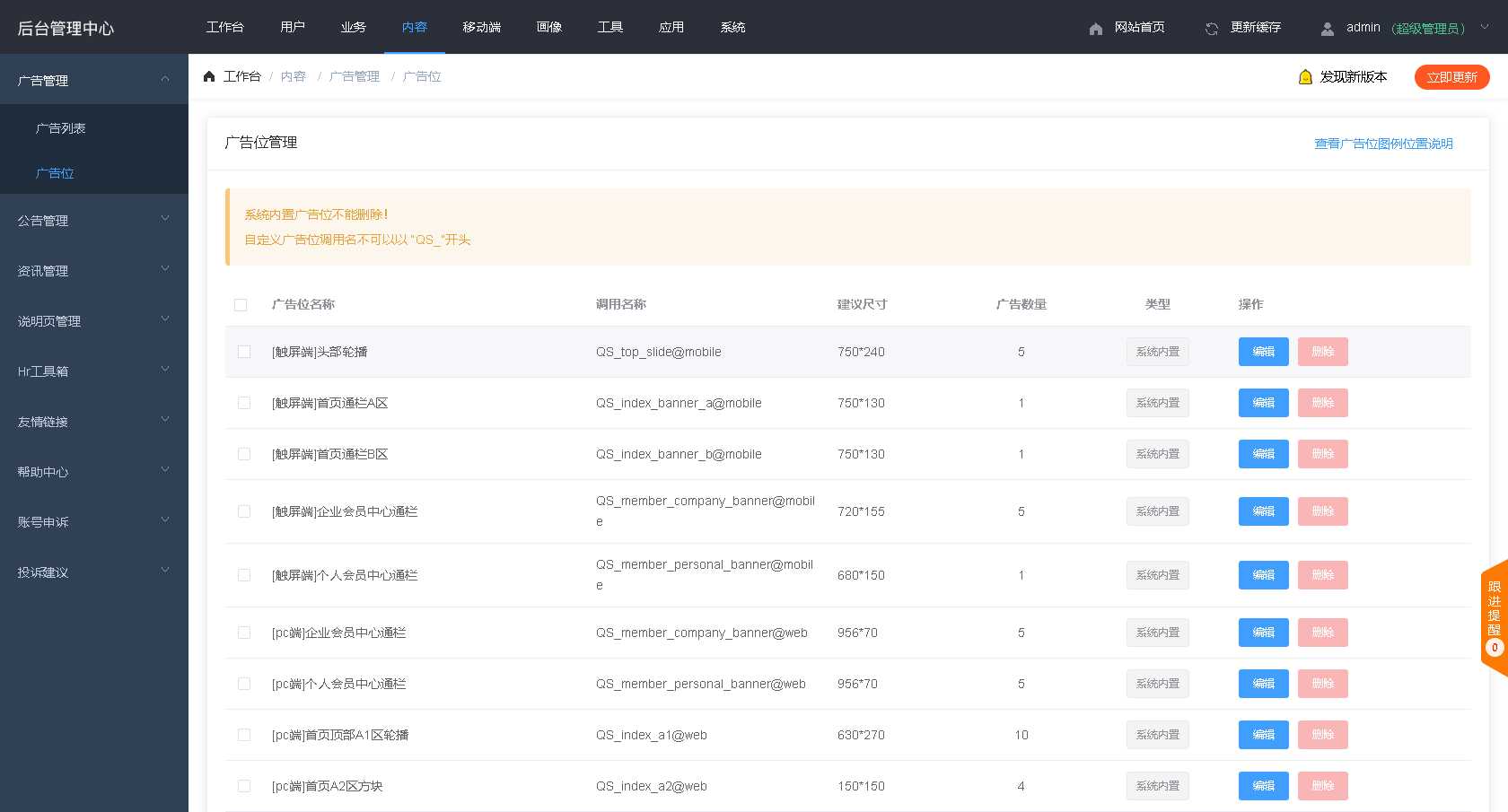
宝塔搭建实战php源码人才求职管理系统后台端thinkphp源码(一)
大家好啊,我是测评君,欢迎来到web测评。 在开源社区里看到了这一套系统,骑士人才系统SE版,搭建测试了,感觉很不错。能够帮助一些想做招聘平台的朋友降低开发成本,就是要注意,想商业使用的话&…...
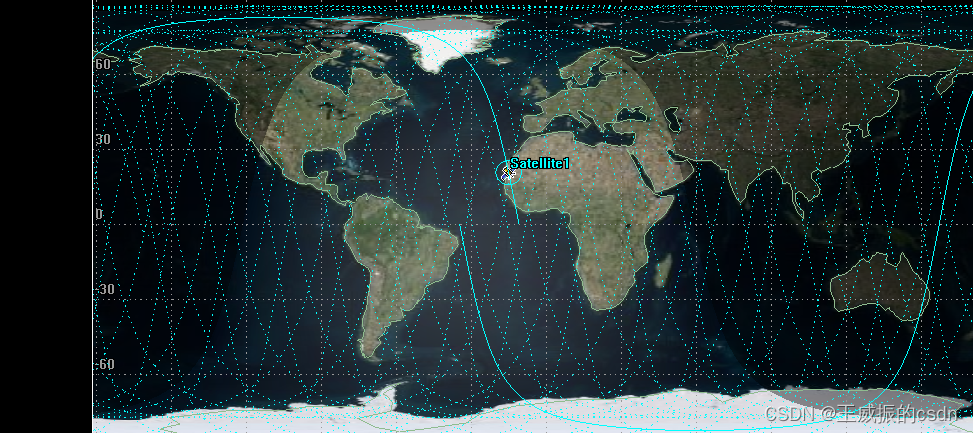
stk 根据六根数文件生成卫星轨迹(一)
先简单介绍下上面的参数。 Propagator预报轨道模型。 TwoBody为二体(开普勒运动模型)。HPOP为高精度轨道模型。目前只用到这两个。 下图为六根数参数 Orbit Epoch:为根数时间(UTC) Semimajor Axis:长半…...
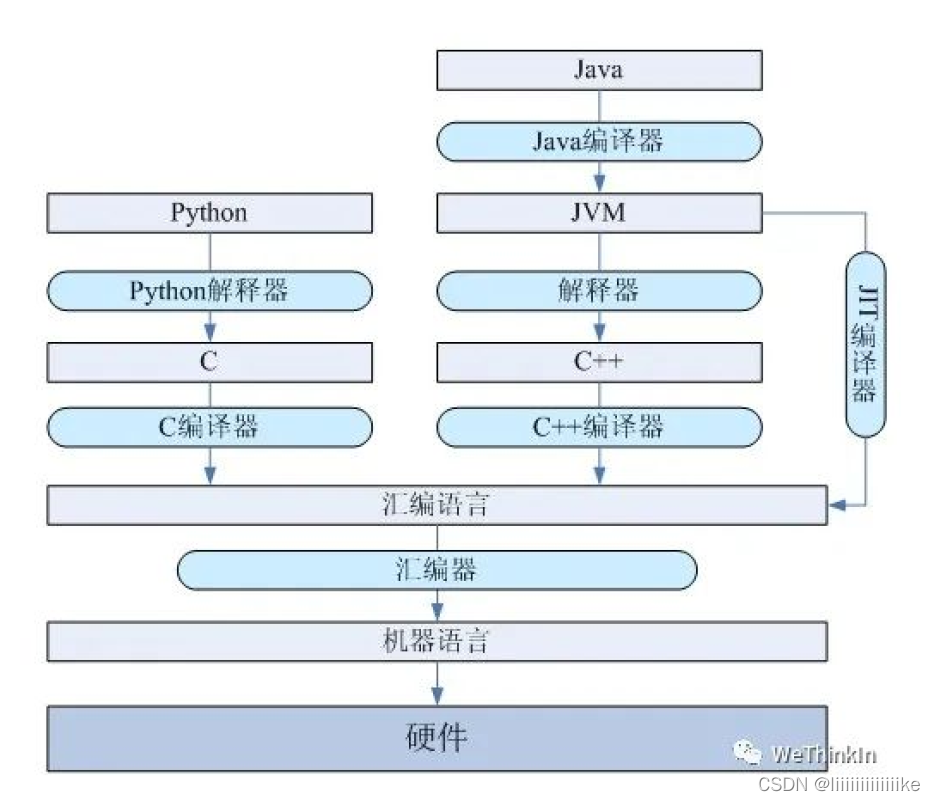
深度学习算法面试常问问题(一)
博主秋招遇到的面试问题以及整理其他面经相关问题,无偿分享~ 项目叙述: 算法需求及应用场景算法的调研和初步方案的制定数据的准备(包括数据标注和数据增强)算法的介绍(包括输入和输出,loss、backbone、训…...
Spring 底层原理与解析 - 容器接口
Spring 底层原理与解析 - 容器接口 BeanFactory 能做哪些事 BeanFactory 与 ApplicaiotnContext 到底是谁提前做完了对象的加载 在之前的一篇关于 Spring 的文章Spring IoC 与容器的初始化中提到过,BeanFactory 接口与 ApplicationContext 接口之间的关系 可以看…...
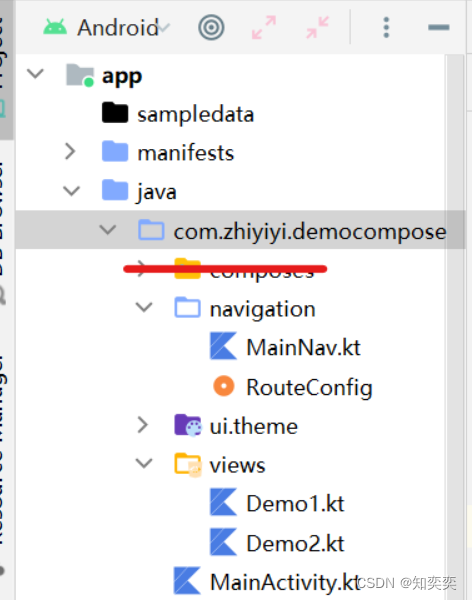
Compose-Navigation简单案例上手
Navigation 快速上手 下面案例简要展示使用 Compose 版本的 Navigation 库来实现两个页面之间的跳转 这是完整的结构(忽略掉红线划过的那个包) 安装适用于 kotlin 的 navigation 依赖 dependencies {implementation("androidx.navigation:navigati…...

855. 考场就座
题目 考场就座 在考场里,一排有 N 个座位,分别编号为 0, 1, 2, …, N-1 。 当学生进入考场后,他必须坐在能够使他与离他最近的人之间的距离达到最大化的座位上。如果有多个这样的座位,他会坐在编号最小的座位上。(另外…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...
