855. 考场就座
题目
- 考场就座
在考场里,一排有 N 个座位,分别编号为 0, 1, 2, …, N-1 。
当学生进入考场后,他必须坐在能够使他与离他最近的人之间的距离达到最大化的座位上。如果有多个这样的座位,他会坐在编号最小的座位上。(另外,如果考场里没有人,那么学生就坐在 0 号座位上。)
返回 ExamRoom(int N) 类,它有两个公开的函数:其中,函数 ExamRoom.seat() 会返回一个 int (整型数据),代表学生坐的位置;函数 ExamRoom.leave(int p) 代表坐在座位 p 上的学生现在离开了考场。每次调用 ExamRoom.leave§ 时都保证有学生坐在座位 p 上。
示例:
输入:[“ExamRoom”,“seat”,“seat”,“seat”,“seat”,“leave”,“seat”], [[10],[],[],[],[],[4],[]]
输出:[null,0,9,4,2,null,5]
解释:
ExamRoom(10) -> null
seat() -> 0,没有人在考场里,那么学生坐在 0 号座位上。
seat() -> 9,学生最后坐在 9 号座位上。
seat() -> 4,学生最后坐在 4 号座位上。
seat() -> 2,学生最后坐在 2 号座位上。
leave(4) -> null
seat() -> 5,学生最后坐在 5 号座位上。
提示:
1 <= N <= 10^9
在所有的测试样例中 ExamRoom.seat() 和 ExamRoom.leave() 最多被调用 10^4 次。
保证在调用 ExamRoom.leave§ 时有学生正坐在座位 p 上。
分析
寻找座位
要实时找到使间距最大化的位置,可以维护一个区间的有序集合。只要能找到最大的区间,就能够确定目标座位。
可以用左端点和右端点 [left, right] 表示一个区间,如果一个学生坐在区间的中间,那么他与两个端点的间距为 (right - left) / 2。根据题意,间距相等时优先选择序号小的座位,则排序区间的比较规则是:
若两个区间的间距不等:选择间距较大的区间
否则:选择序号较小的区间
可以将区间放到一个大顶堆中,这样就可以在 O(1) 时间复杂度下找到满足条件的最大区间 m。当一个学生坐下时,需要将 m 从大顶堆移除,并根据学生坐下的位置将新产生的区间放入到大顶堆中。假设区间为 m = [a, b],那么学生应该坐到 c = (a+b) / 2,则新产生的区间为:[a,c] 和 [c, b]。
离开座位
至此,只分析了没有学生会离开座位的情况。如果一个学生离开了座位,那么由他坐下而产生的新区间都将失效,此外还需要将因为学生离开而产生的新区间放入到大顶堆中。
我们可以延迟删除大顶堆中失效的区间。
为了确定大顶堆中的区间是否失效,可以设置一个有序集合 set 表示当前有学生的座位号。验证一个区间 [a, b] 有效的条件为:
- 能从
set里面找到a和b,即两个端点都有学生; a和b之间没有其它值,即没有学生坐在这个区间里。
其它
上述分析不包含边界条件。首先想到通过在位置 -1 和位置 n 放置哨兵,避免特殊情况的判断。但题目要求第一个位置为 0 号座位,所以这种方法行不通。
可以单独计算学生坐在边沿的情况:
- 如果当前没有学生就座,直接选择 0 号座位;
- 如果边沿座位比某区间中央的座位更佳,则选择边沿座位。
代码
struct interval {int left, right;
};struct CompByLen {bool operator()(const interval a, const interval b) const {int da = a.right - a.left, db = b.right - b.left;return da / 2 < db / 2 || da / 2 == db / 2 && a.left > b.left;}
};class ExamRoom {
public:ExamRoom(int n) : n_(n) {}int seat() {if (seat_taken_.empty()) {seat_taken_.insert(0);return 0;}int llen = *seat_taken_.begin(), rlen = n_ - 1 - *seat_taken_.rbegin();while (seat_taken_.size() >= 2) {auto p = interval_by_len_.top();if (!isValidInterval(p)) {interval_by_len_.pop();continue;}int len = p.right - p.left;if (len / 2 <= llen || len / 2 < rlen) {// Seat on the side is better.break;}interval_by_len_.pop();int pos = p.left + len / 2;interval_by_len_.push({p.left, pos});interval_by_len_.push({pos, p.right});seat_taken_.insert(pos);return pos;}if (llen >= rlen) {interval_by_len_.push({0, *seat_taken_.begin()});seat_taken_.insert(0);return 0;} else {interval_by_len_.push({*seat_taken_.rbegin(), n_ - 1});seat_taken_.insert(n_ - 1);return n_ - 1;}}void leave(int p) {auto it = seat_taken_.find(p);if (it != seat_taken_.begin() && it != prev(seat_taken_.end())) {interval_by_len_.push({*prev(it), *next(it)});}seat_taken_.erase(it);}private:int n_;set<int> seat_taken_;priority_queue<interval, vector<interval>, CompByLen> interval_by_len_;bool isValidInterval(interval &p) {// Have students both sides && no student in the middle.return seat_taken_.count(p.left) > 0 && seat_taken_.count(p.right) > 0 &&*next(seat_taken_.find(p.left)) == p.right;}
};
相关文章:

855. 考场就座
题目 考场就座 在考场里,一排有 N 个座位,分别编号为 0, 1, 2, …, N-1 。 当学生进入考场后,他必须坐在能够使他与离他最近的人之间的距离达到最大化的座位上。如果有多个这样的座位,他会坐在编号最小的座位上。(另外…...
)
k8s之ingress(二)
文章目录k8s之ingress1.1、Kubernetes 暴露服务的方式:1.2 基本概念1.3为什么需要Ingress资源1.4 Ingress的工作原理1.5ingress 暴露服务的方式总结k8s之ingress 1.1、Kubernetes 暴露服务的方式: Kubernetes暴露服务的方式目前只有三种:LoadBlancer Service、Nod…...
linux下监测串口数据
在编写上下位机通信代码时,需要分阶段测试,确保下位机,线路,上位机都OK. 一.检查设备数据传出 1.确定下位机的串口参数 如果波特率有问题,可能会…...
三分钟深入理解闭包(附详解实例))
【面试之闭包】前端面试那些事(2)三分钟深入理解闭包(附详解实例)
目录1、什么是闭包,什么是作用域1.1 变量作用域1.2 闭包是啥?如何改变变量调用格局1.3 闭包的特性2、怎么用闭包,闭包实例应用2.1 常见闭包实例2.2 闭包异步函数的应用2.3 柯里化的应用3、闭包的优缺点3.1 优点3.2 缺点4、片尾彩蛋【写在前面…...

深入浅出带你学习WebSphere中间件漏洞
前言 上一篇文章给大家介绍了中间件glassfish的一些常见漏洞以及利用方法,今天我给大家带来的是WebSphere中间件的常见漏洞以及这些漏洞的利用方法,下面我们首先介绍一下WebSphere中间件是什么,然后展开来讲关于该中间件的漏洞。 WebSphere…...

如何一眼分辨是C还是C++
C语言的历史C语言是由贝尔实验室的Dennis Ritchie在20世纪70年代初开发的一种通用程序设计语言。在早期的计算机时代,许多计算机使用不同的汇编语言编写程序,这导致了程序的可移植性和代码的可重用性很低。因此,Dennis Ritchie在开发C语言时试…...
CMake系列:正确使用多配置编译系统
目录 常见错误 问题现象 正确做法 if指令应该什么时候使用 活学活用 把IF指令用于多配置编译系统是很多初学者容易犯下的错误。这篇文章启示性的教你如何正确理解、使用CMake的多配置编译系统。 常见错误 以Debug和Release配置有不同的宏定义为例,如下所示&a…...
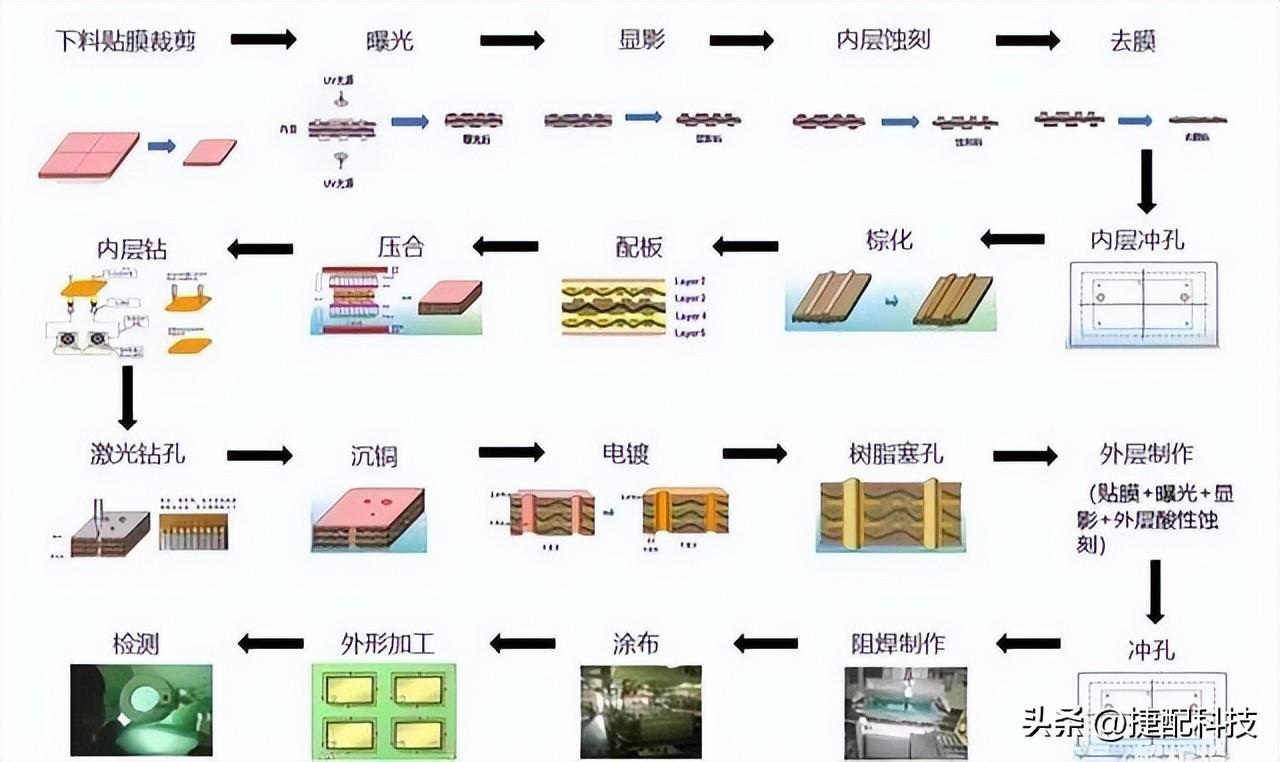
PCB中的HDI板生产中的变化
关键词:HDI概述 HDI发展演变 HDI生产难点如果把一整个电子产业比作浩瀚的宇宙,那些智能电子设备就像宇宙中闪耀的星光,当你以“上帝”的视角手持放大镜去观察时,这些闪烁的星光点点其实都是一个个由精密的“自然规律”所“设计”好…...

程序分析与神经网络后门
原文来自微信公众号“编程语言Lab”:程序分析与神经网络后门 搜索关注“编程语言Lab”公众号(HW-PLLab)获取更多技术内容! 欢迎加入编程语言社区 SIG-程序分析,了解更多程序分析相关的技术内容。 加入方式:…...

redis主从哨兵模式
一.为什么用redis主从模式 1.数据备份:主从复制实现数据的热备份。 2.故障恢复:当主节点出现问题时,由从节点提供服务,实现快速恢复。 3.负载均衡:读写分离,主节点提供写服务,从节点提供读服务。在写少读多时提高Redis的并发。 二.为什么使用哨兵模式 主要用于主节…...
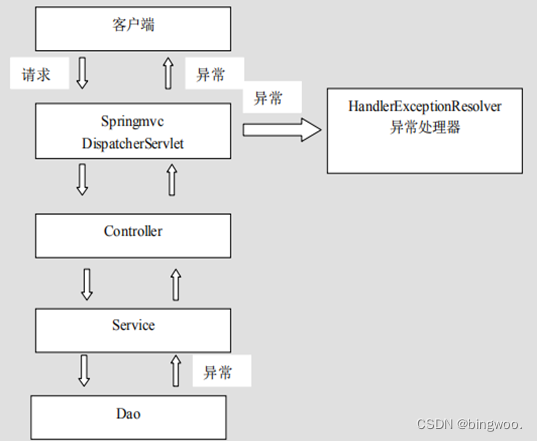
Spring 系列之 MVC
Spring 系列文章目录 文章目录Spring 系列文章目录前言一、介绍二、项目搭建1.创建空项目2.设置maven和lombok3.创建maven web module4. 配置Tomcat启动运行项目(选择local本地)5. 导入jar依赖包6.在web.xml中配置DispatcherServlet7. 加入SpringMVC的配…...
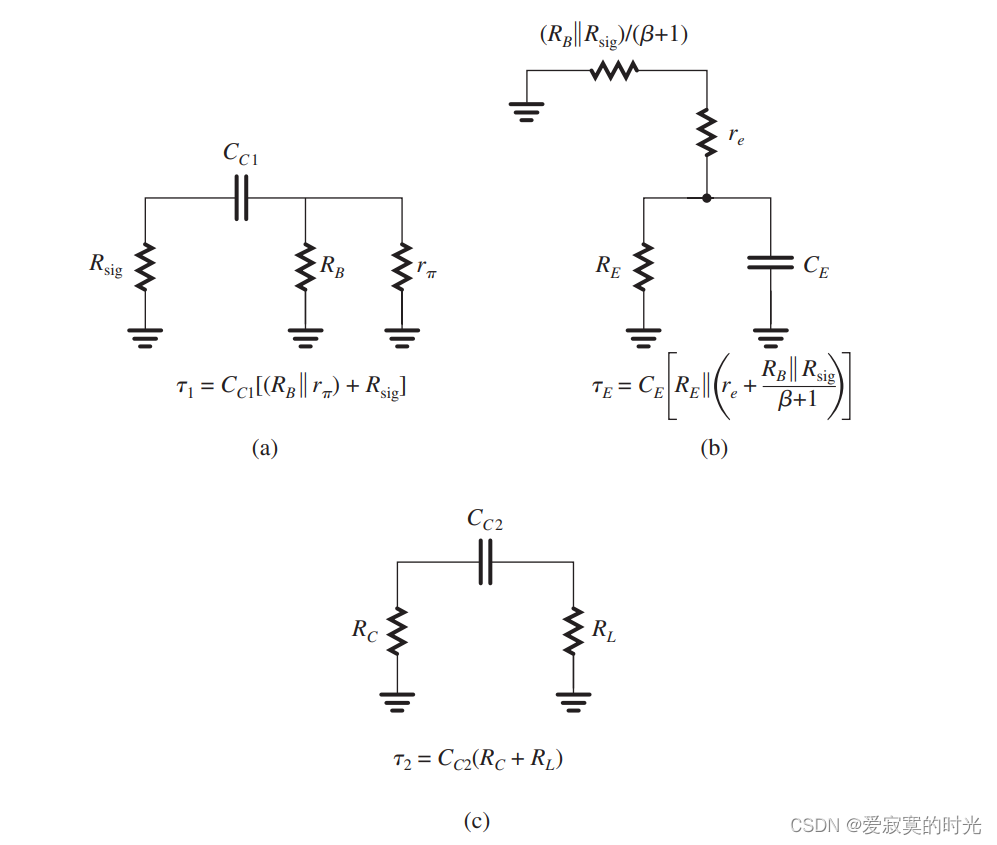
电子技术——分立CS和CE放大器的低频响应
电子技术——分立CS和CE放大器的低频响应 我们之前在学习放大器中从来没有关系过信号频率对放大器的影响,也就是说我们默认放大器具有无限的带宽,这当然不符合现实逻辑。为了说明这一点,我们使用下图: 上图描述了MOS或BJT分立电路…...

代码随想录【Day16】| 104. 二叉树的最大深度、111. 二叉树的最小深度、222. 完全二叉树的节点个数
104. 二叉树的最大深度 题目链接 题目描述: 给定一个二叉树,找出其最大深度。 二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。 说明: 叶子节点是指没有子节点的节点。 示例: 给定二叉树 [3,9,20,null,null,15,7],…...

状态机图、通信图题
1.下列关于通信图与顺序图中的对象的相同点的叙述.正确的是(D)。A.两种图中都可以表示对象的创建和销毁B.对象在两种图中的位置都没有任何限制C.对象在两种图中的表示方式完全一致D.对象名在两种图中的表示完全一致2.下列关于通信图的说法错误的是(C)。A.通信图是对一次交互过程…...

分布式文件存储Minio学习入门
文章目录一、分布式文件系统应用场景1. Minio介绍Minio优点2. MinIO的基础概念、3. 纠删码ES(Erasure Code)4. 存储形式5. 存储方案二、Docker部署单机Minio三、minio纠删码模式部署四、分布式集群部署分布式存储可靠性常用方法冗余校验分布式Minio优势运行分布式minio使用dock…...
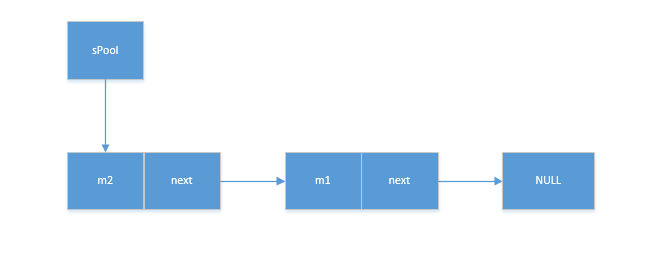
handler解析(4)-Message及Message回收机制
Message中可以携带的信息 Message中可以携带的数据比较丰富,下面对一些常用的数据进行了分析。 /*** 用户定义的消息代码,以便当接受到消息是关于什么的。其中每个Hanler都有自己的命名控件,不用担心会冲突*/ public int what; /*** 如果你…...

Linux使用定时任务监控java进程并拉起
需求描述: 设计一个脚本,通过Linux定时任务,每分钟执行一次,监控jar包进程是否存在,存在则不做动作,不存在则重新拉起jar包程序。 定时任务配置: */1 * * * * bash -x /root/myfile/jars/che…...
Win 10电脑摄像头提示错误代码0xa00f4244怎么办?
如果你的Windows 10电脑无法打开摄像头,提示“我们找不到你的摄像头”的错误消息,错误代码是0xA00F4244,原因可能是杀毒软件阻止了摄像头,或者是摄像头驱动程序有问题。 小编为你整理了摄像头错误代码0xA00F4244的解决方法&#…...
MFC消息机制
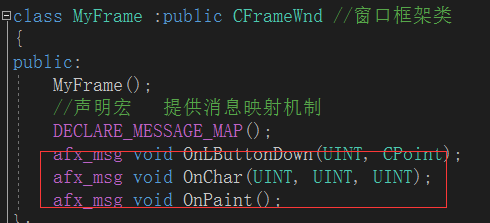
1.消息映射消息映射是一个将消息和成员函数相互关联的表。比如,框架窗口接收到一个鼠标左击消息,MFC将搜索该窗口的消息映射,如果存在一个处理WM_LBUTTTONDOWN消息的处理程序,然后就调用OnButtonDown。2.消息映射机制2.1 声明宏 写…...

全国计算机等级考试报名照片要求以及证件照制作教程
马上就全国计算机等级考试就要开始了,相信现在很多同学都在网上进行报名呢,报名的时候肯定需要用到个人证件照片,所以问题来了,我们怎么自己制作证件照片呢?计算机等级考试报名时对证件照都有哪些要求呢?该…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...

《Docker》架构
文章目录 架构模式单机架构应用数据分离架构应用服务器集群架构读写分离/主从分离架构冷热分离架构垂直分库架构微服务架构容器编排架构什么是容器,docker,镜像,k8s 架构模式 单机架构 单机架构其实就是应用服务器和单机服务器都部署在同一…...

文件上传漏洞防御全攻略
要全面防范文件上传漏洞,需构建多层防御体系,结合技术验证、存储隔离与权限控制: 🔒 一、基础防护层 前端校验(仅辅助) 通过JavaScript限制文件后缀名(白名单)和大小,提…...
