day44【代码随想录】动态规划之零钱兑换II、组合总和 Ⅳ、零钱兑换
文章目录
- 前言
- 一、零钱兑换II(力扣518)
- 二、组合总和 Ⅳ(力扣377)
- 三、零钱兑换(力扣322)
- 总结
前言
1、零钱兑换II
2、组合总和 Ⅳ
3、零钱兑换
一、零钱兑换II(力扣518)
给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。
请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。
假设每一种面额的硬币有无限个。
类似与之前的目标和问题(01背包)求有多少种组合方式
目标和

分析
题目描述中是凑成总金额的硬币组合数,为什么强调是组合数呢?
例如示例一:
5 = 2 + 2 + 1
5 = 2 + 1 + 2
这是一种组合,都是 2 2 1。
如果问的是排列数,那么上面就是两种排列了。
组合不强调元素之间的顺序,排列强调元素之间的顺序
每个硬币可以重复使用,完全背包问题
整数amount 相当于完全背包问题中的背包容量
组合数:不强调元素之间的顺序
动规五部曲:
1、确定dp数组以及下标的含义
dp[j] :表示总金额为j时有dp[j]种方式
2、确定递推公式
dp[j] += dp[j - coins[i]];
3、dp数组如何初始化
dp[0]一定是1,因为dp[0]是在公式中一切递推结果的起源,如果dp[0]是0的话,递推结果将都是0。
4、确定遍历顺序
外层for循环遍历物品(钱币),内层for遍历背包(金钱总额)===组合数
是否可以颠倒?
不可以
外层for遍历背包(金钱总额),内层for循环遍历物品(钱币) ===排列数
class Solution {public int change(int amount, int[] coins) {int[] dp = new int[amount+1];//初始化 类似于目标和问题dp[0]=1;for(int i = 0; i<coins.length;i++){for(int j=coins[i];j<=amount;j++){dp[j] += dp[j-coins[i]];}}return dp[amount];}
}

二、组合总和 Ⅳ(力扣377)
给你一个由 不同 整数组成的数组 nums ,和一个目标整数 target 。请你从 nums 中找出并返回总和为 target 的元素组合的个数。

分析 :
元素可以重复使用 --> 完全背包问题
求排列数 -->遍历顺序 外层循环背包容量 内层循环元素个数
class Solution {public int combinationSum4(int[] nums, int target) {int[] dp = new int[target+1];dp[0]=1;for(int j=0;j<=target;j++){for(int i = 0;i<nums.length;i++){if(j-nums[i]>=0){dp[j] += dp[j-nums[i]]; }}} return dp[target];}
}

三、零钱兑换(力扣322)
给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。
计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。
你可以认为每种硬币的数量是无限的。

分析:
每种硬币的数量是无限的,可以看出是典型的完全背包问题。
1、确定dp数组以及下标的含义
dp[j]:凑足总额为j所需钱币的最少个数为dp[j]
2、确定递推公式
凑足总额为j - coins[i]的最少个数为dp[j - coins[i]],那么只需要加上一个钱币coins[i]即dp[j - coins[i]] + 1就是dp[j]
dp[j] = Math.min(dp[j], dp[j-coins[j]]+1)
3、dp数组初始化
在测试用例中可以发现 dp[0] = 0;
考虑到递推公式的特性,dp[j]必须初始化为一个最大的数,否则就会在min(dp[j - coins[i]] + 1, dp[j])比较的过程中被初始值覆盖。
所以下标非0的元素都是应该是最大值。
4、确定遍历顺序
本题求钱币最小个数,那么钱币有顺序和没有顺序都可以,都不影响钱币的最小个数。
所以本题并不强调集合是组合还是排列。
class Solution {public int coinChange(int[] coins, int amount) {int[] dp = new int[amount+1];int max = Integer.MAX_VALUE;//初始化为最大值for(int i=0;i<dp.length;i++){dp[i] = max;}dp[0] = 0;//遍历for(int i=0;i<coins.length;i++){for(int j=coins[i];j<=amount;j++){if(dp[j-coins[i]]!=max){dp[j] = Math.min(dp[j],dp[j-coins[i]]+1);}}}return dp[amount] == max? -1:dp[amount];}
}

总结
如果求组合数就是外层for循环遍历物品,内层for遍历背包。
如果求排列数就是外层for遍历背包,内层for循环遍历物品
相关文章:

day44【代码随想录】动态规划之零钱兑换II、组合总和 Ⅳ、零钱兑换
文章目录前言一、零钱兑换II(力扣518)二、组合总和 Ⅳ(力扣377)三、零钱兑换(力扣322)总结前言 1、零钱兑换II 2、组合总和 Ⅳ 3、零钱兑换 一、零钱兑换II(力扣518) 给你一个整数…...
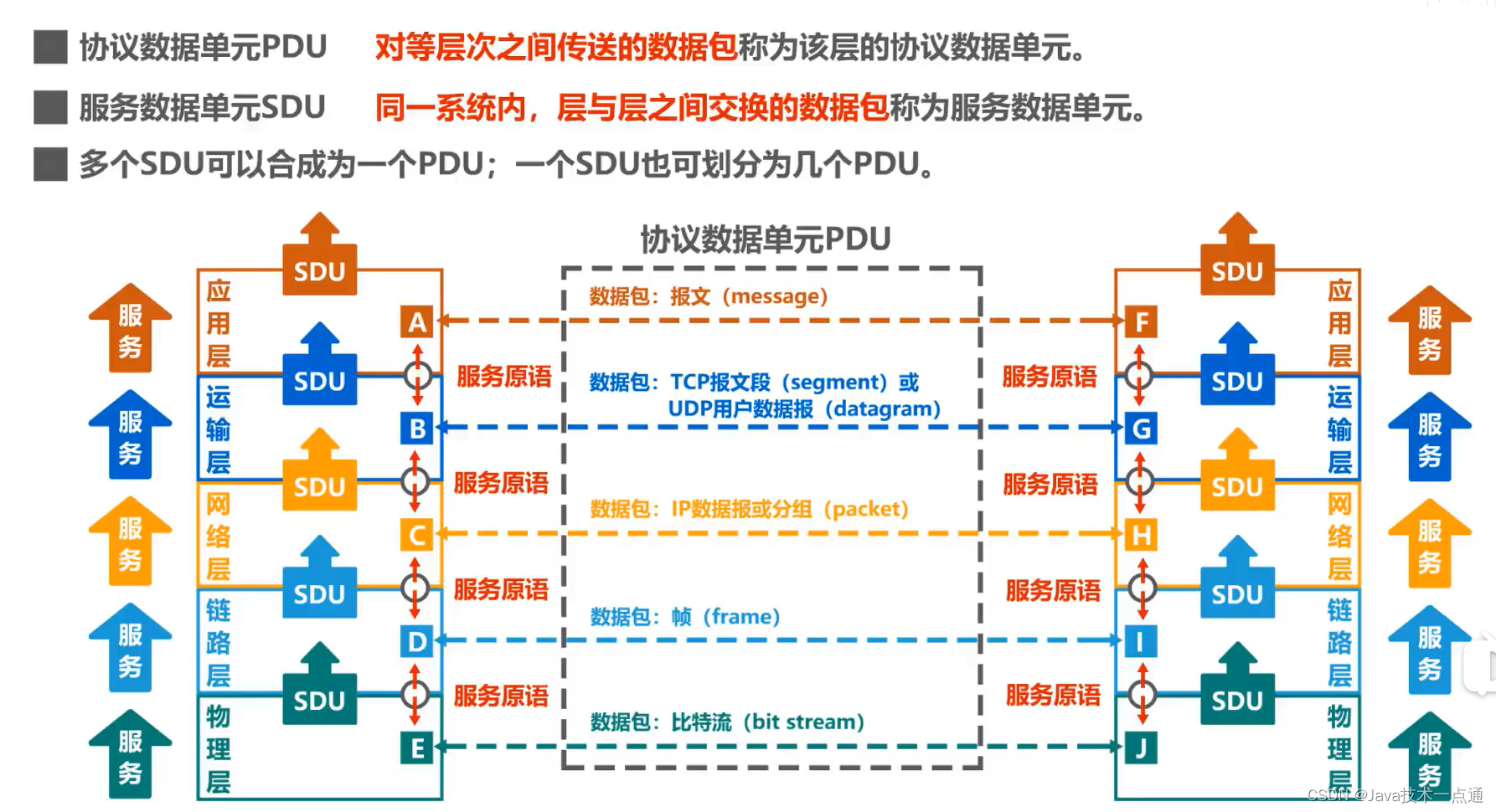
计算机网络第1章(概述)学习笔记
❤ 作者主页:欢迎来到我的技术博客😎 ❀ 个人介绍:大家好,本人热衷于Java后端开发,欢迎来交流学习哦!( ̄▽ ̄)~* 🍊 如果文章对您有帮助,记得关注、点赞、收藏、…...
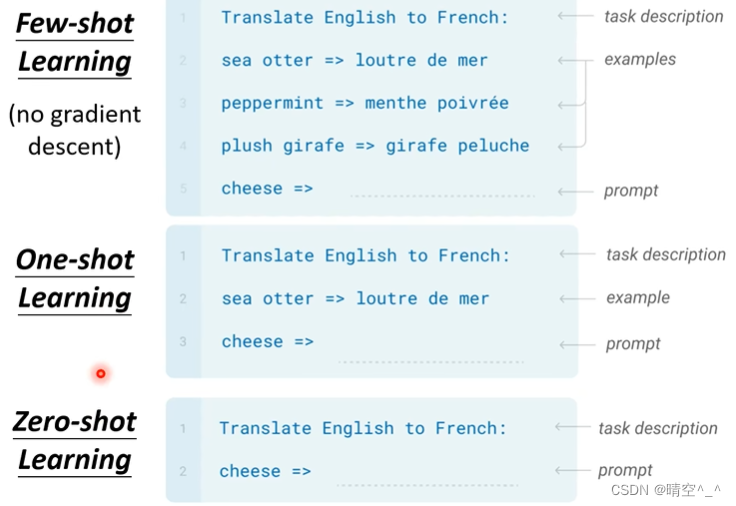
GPT-3(Language Models are Few-shot Learners)简介
GPT-3(Language Models are Few-shot Learners) 一、GPT-2 1. 网络架构: GPT系列的网络架构是Transformer的Decoder,有关Transformer的Decoder的内容可以看我之前的文章。 简单来说,就是利用Masked multi-head attention来提取文本信息&a…...
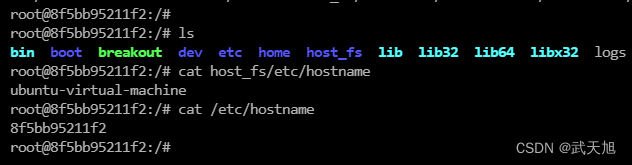
容器安全风险and容器逃逸漏洞实践
本文博客地址:https://security.blog.csdn.net/article/details/128966455 一、Docker存在的安全风险 1.1、Docker镜像存在的风险 不安全的第三方组件:用户自己的代码依赖若干开源组件,这些开源组件本身又有着复杂的依赖树,甚至…...

2023年美赛B题-重新想象马赛马拉
背景 肯尼亚的野生动物保护区最初主要是为了保护野生动物和其他自然资源资源。肯尼亚议会于2013年通过了《野生动物保护和管理法》提供更公平的资源共享,并允许替代的、以社区为基础的管理工作[1]。此后,肯尼亚增加了修正案,以解决立法中的空…...
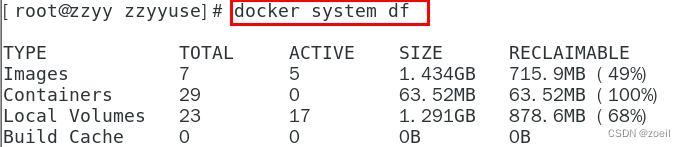
Docker常用命令总结
目录 一、帮助启动类命令 (1)启动docker (2)停止docker (3)重启docker (4)查看docker (5)设置开机自启 (6)查看docker概要信息…...
mac环境,安装NMP遇到的问题
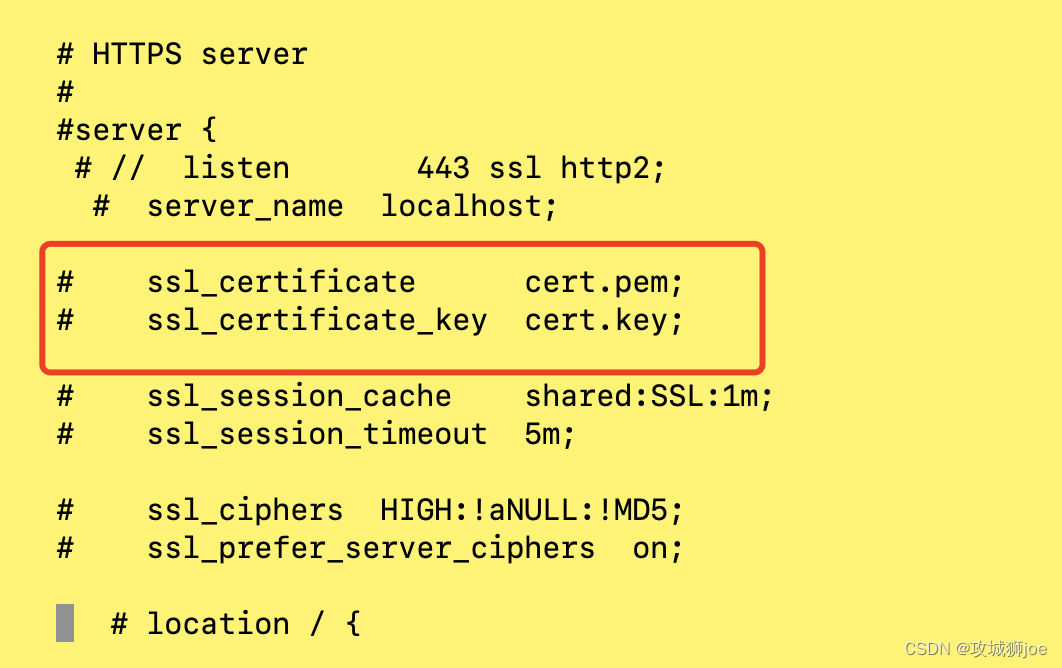
一 背景 项目开发中,公司项目需要使用本地的环境运行,主要是php这块的业务。没有使用docker来处理,重新手动撸了一遍。记录下其中遇到的问题; 二 遇到的问题 2.1 Nginx的问题 brew install nginx后,启动nginx,报错如下:nginx: [emerg] no "ssl_certificate" …...

Web Worker 与 SharedWorker 的介绍和使用
目录一、Web Worker1 Web Worker 是什么2 Web Worker 使用3 简单示例二、SharedWorker2.1 SharedWorker 是什么2.2 SharedWorker 的使用方式2.3 多页面数据共享的例子一、Web Worker 1 Web Worker 是什么 Web Worker是 HTML5 标准的一部分,这一规范定义了一套 API…...

React:Redux和Flux
React,用来构建用户界面,它有三个特点: 作为view,构建上用户界面虚拟DOM,目的就是高性能DOM渲染【diff算法】、组件化、多端同构单向数据流,是一种自上而下的渲染方式。Flux 在一个React应用中,UI部分是由无数个组件嵌套构成的,组件和组件之间就存在层级关系,也就是父…...

TypeScript 学习之Class
基本使用 class Greeter {// 属性greeting: string;// 构造函数constructor(message: string) {// 用this 访问类的属性this.greeting message;}// 方法greet() {return Hello, this.greeting;} } // 实例化 let greeter new Greeter(World);声明了一个Greeter类ÿ…...
doris - 数仓 拉链表 按天全量打宽表性能优化
数仓 拉链表 按天全量打宽性能优化现状描述优化现状描述 1、业务历史数据可以变更 2、拉链表按天打宽 3、拉链表模型分区字段设计不合理,通用的过滤字段没有作为分区分桶字段 4、拉链表表数据量略大、模型数据分区不合理和服务器资源限制,计算任务执行超…...

服务器虚拟化及优势
服务器虚拟化是从一台物理服务器创建多个服务器实例的过程。每个服务器实例代表一个隔离的虚拟环境。在每个虚拟环境中,都可以运行单独的操作系统。 1.更有效的资源调配 使用虚拟化技术大大节省了所占用的空间,减少了数据中心里服务器和相关硬件的数量。…...
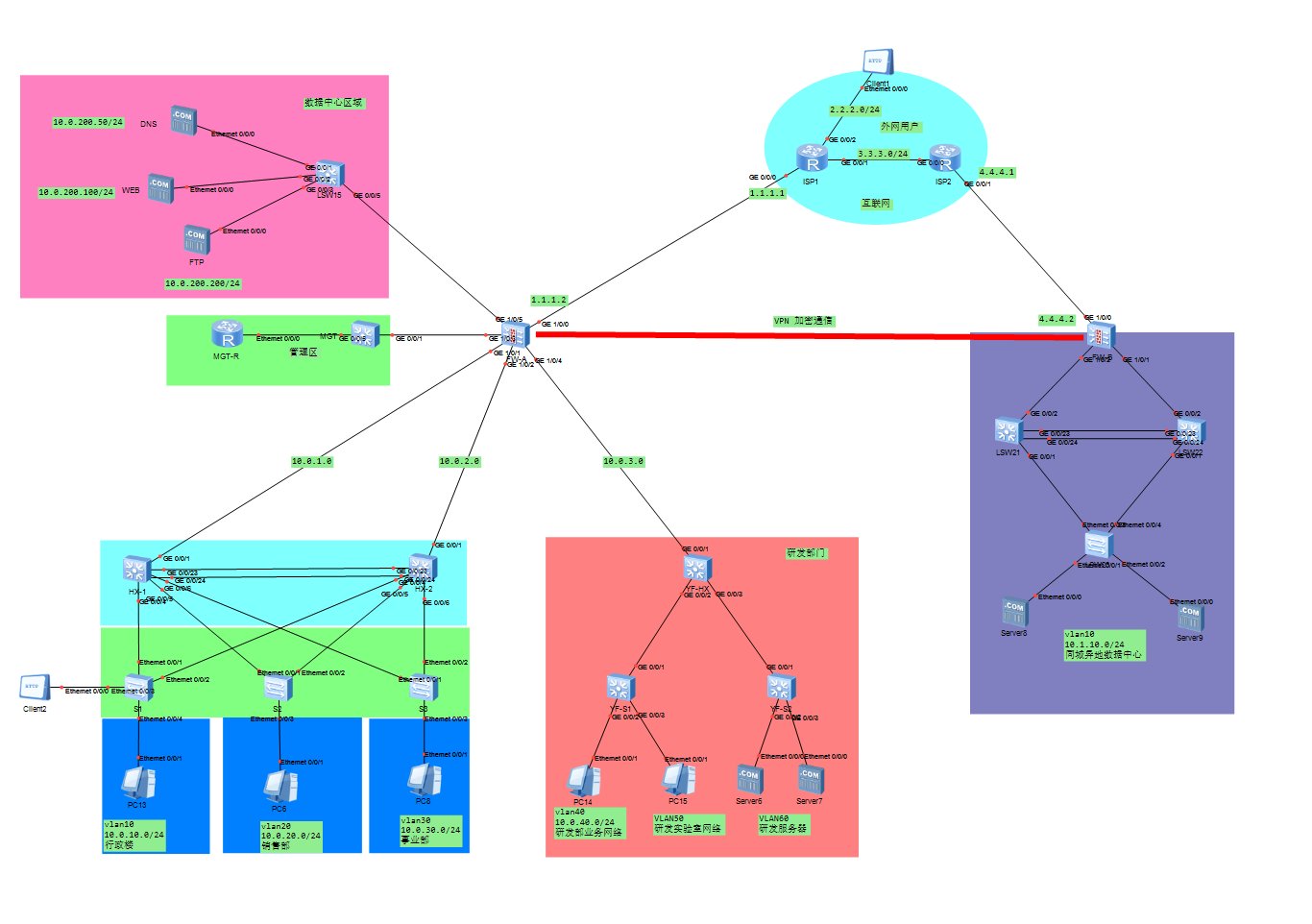
华为ensp模拟校园网/企业网实例(同城灾备及异地备份中心保证网络安全)
文章简介:本文用华为ensp对企业网络进行了规划和模拟,也同样适用于校园、医院等场景。如有需要可联系作者,可以根据定制化需求做修改。作者简介:网络工程师,希望能认识更多的小伙伴一起交流,私信必回。一、…...

git命令篇(持续更新中)
首先介绍这个网页:https://learngitbranching.js.org/?localezh_CN --提交命令 git commit --创建分支 git branch <分支名> --切换分支 git checkout <分支名> --合并分支 (合并到主分支去,把我合并到谁的身上去) 自己写的分支合并到主线…...
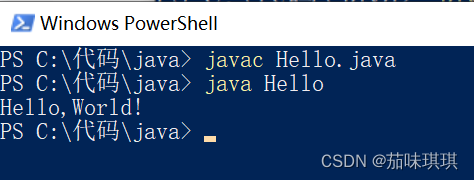
用记事本实现“HelloWorld”输出
一、在任意文件夹中创建一个新的文本文档文件并写入以下代码 public class Hello{public static void main (String[] args){System.out.print("Hello,World!");} } 二、修改文件名称及文件类型为 Hello.java 特别注意:文件命名必须与代码中类的名称相同…...
Python基础1
1. 注释 单行注释:以#开头。一般建议注释和内容用空格隔开。 多行注释:以一对三个双引号括起来的内容是注释。“““示例注释”””。 2. 数据类型 验证数据类型的方法:type(被查看类型的数据)。 注意:…...

4.2 双点双向路由重发布
1. 实验目的 熟悉双点双向路由重发布的应用场景掌握双点双向路由重发布的配置方法2. 实验拓扑 双点双向路由重发布如图4-6所示: 图4-6:双点双向路由重发布 3. 实验步骤 IP地址的配置R1的配置 <Huawei>system-v…...

AcWing《蓝桥杯集训·每日一题》—— 3768 字符串删减
AcWing《蓝桥杯集训每日一题》—— 3768. 字符串删减 文章目录AcWing《蓝桥杯集训每日一题》—— 3768. 字符串删减一、题目二、解题思路三、代码实现本次博客我是通过Notion软件写的,转md文件可能不太美观,大家可以去我的博客中查看:北天的 …...

第五天笔记
1. 简述图片验证码使用流程? 1.前段生成UUID随机值,作为GET请求参数 2.后端试图进行判断,调用工具类来生成图片验证码和内容 3.将验证码内容使用redis保存到本地,前端传入的uuid作为key, 4.在前段输入获取到的图片验证码,想后端发…...
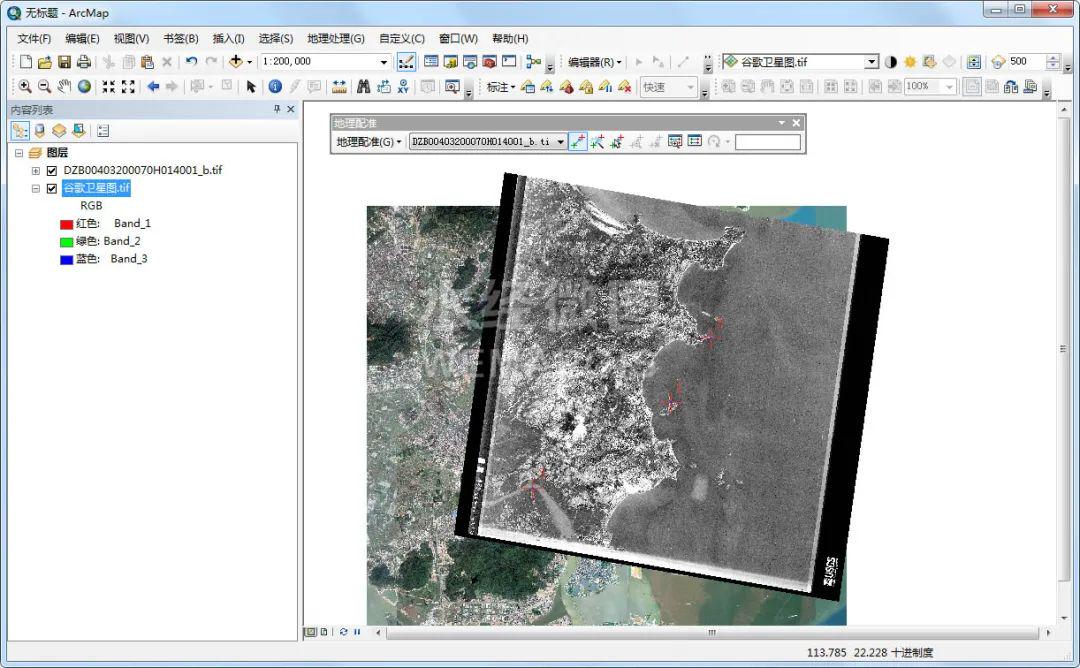
如何使用ArcGIS进行地理配准
1.概述 对于GIS数据而言,坐标信息是灵魂,有了坐标信息之后才能和别的数据结合使用,之前有介绍过矢量数据定义坐标信息的方法,针对栅格图,这里为大家介绍一下通过地理配准增加坐标信息的方法,希望能对你有所…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...
