day43【代码随想录】动态规划之一和零、完全背包理论基础
文章目录
- 前言
- 一、一和零(力扣474)
- 二、完全背包
前言
1、一和零
2、完全背包理论基础
一、一和零(力扣474)
求装满这个背包最多有多少个物品
给你一个二进制字符串数组 strs 和两个整数 m 和 n 。
请你找出并返回 strs 的最大子集的长度,该子集中 最多 有 m 个 0 和 n 个 1 。
如果 x 的所有元素也是 y 的元素,集合 x 是集合 y 的 子集 。

背包容量是二维的 m个0 n个1 限制
思路:
动规五部曲
1、确定dp[]数组以及下标含义
dp[i][j]:i个0 j个1 最多装了dp[i][j]个物品
2、确定递推公式
dp[i][j] 可以由前一个strs里的字符串推导出来,strs里的字符串有zeroNum个0,oneNum个1。
dp[i][j] 就可以是 dp[i - zeroNum][j - oneNum] + 1。
然后我们在遍历的过程中,取dp[i][j]的最大值。
所以递推公式:dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);
对比下01背包的递推公式:dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
对比一下就会发现,字符串的zeroNum和oneNum相当于物品的重量(weight[i]),字符串本身的个数相当于物品的价值(value[i])。
这就是一个典型的01背包! 只不过物品的重量有了两个维度而已。
3、dp数组如何初始化
01背包的dp数组初始化为0就可以。
4、确定遍历顺序
外层for循环遍历物品,内层for循环遍历背包容量且从后向前遍历
5、举例推导dp数组
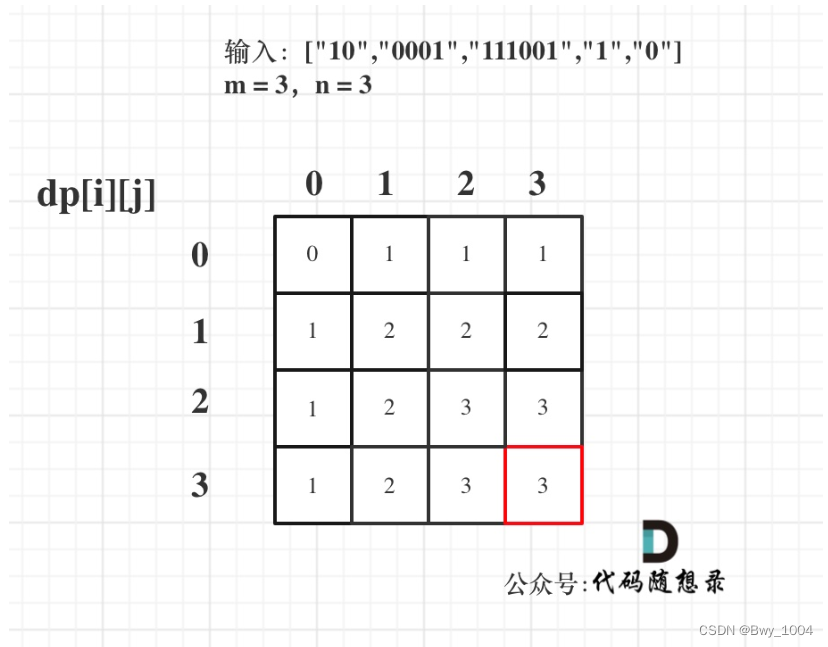
以输入:[“10”,“0001”,“111001”,“1”,“0”],m = 3,n = 3为例
最后dp数组的状态如下所示:
class Solution {public int findMaxForm(String[] strs, int m, int n) {int[][] dp = new int[m+1][n+1];int oneNum;int zeroNum;for(int x = 0; x<strs.length; x++){oneNum = 0;zeroNum = 0;for(char ch : strs[x].toCharArray()){if( ch == '0'){zeroNum++;}else oneNum++;}for(int i=m;i>=zeroNum;i--){for(int j=n;j>=oneNum;j--){dp[i][j] = Math.max(dp[i][j],dp[i-zeroNum][j-oneNum]+1);}}}return dp[m][n];}
}

二、完全背包
完全背包和01背包的区别所在: 物品在完全背包中可以使用无数次。
而在01背包一维dp数组中,倒序遍历背包容量就是为了保证每个物品只取一次,那么如何能让这个物品无限次使用呢?改为正序遍历
for(int i = 0; i < weight.length; i++) { // 遍历物品for(int j = weight[i]; j =< bagWeight; j++) { // 遍历背包容量dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);}
}
遍历顺序:
两层for循环可以相互颠倒
遍历物品在外层循环,遍历背包容量在内层循环(按行),状态如图:
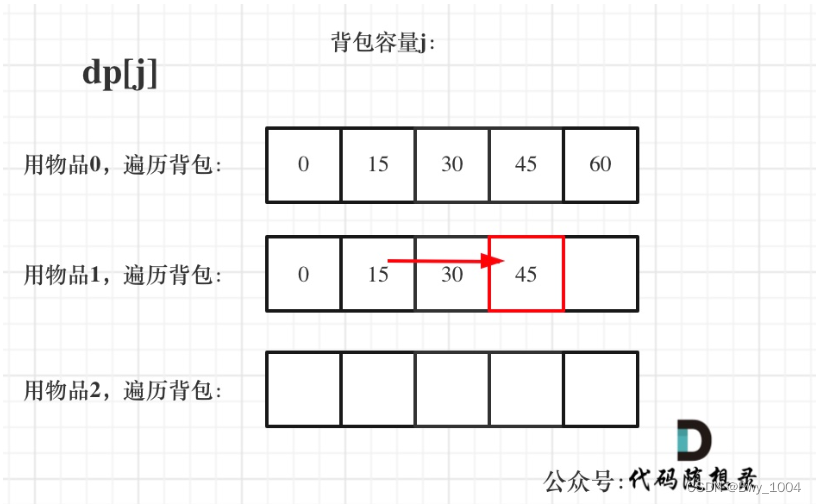
for (int i = 0; i < weight.length; i++){ // 遍历物品for (int j = weight[i]; j <= bagWeight; j++){ // 遍历背包容量dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);}}
遍历背包容量在外层循环,遍历物品在内层循环(按列),状态如图:
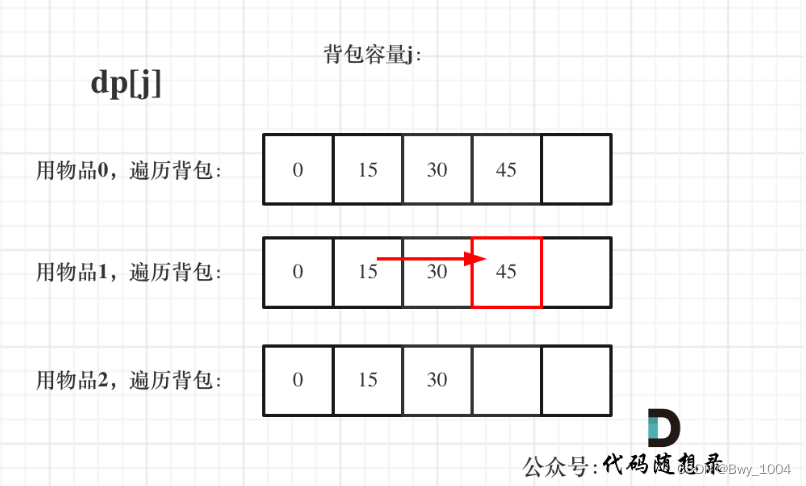
for (int i = 1; i <= bagWeight; i++){ // 遍历背包容量for (int j = 0; j < weight.length; j++){ // 遍历物品if (i - weight[j] >= 0){dp[i] = Math.max(dp[i], dp[i - weight[j]] + value[j]);}}
完整代码:
//先遍历物品,再遍历背包
private static void testCompletePack(){int[] weight = {1, 3, 4};int[] value = {15, 20, 30};int bagWeight = 4;int[] dp = new int[bagWeight + 1];for (int i = 0; i < weight.length; i++){ // 遍历物品for (int j = weight[i]; j <= bagWeight; j++){ // 遍历背包容量dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);}}for (int maxValue : dp){System.out.println(maxValue + " ");}
}
相关文章:

day43【代码随想录】动态规划之一和零、完全背包理论基础
文章目录前言一、一和零(力扣474)二、完全背包前言 1、一和零 2、完全背包理论基础 一、一和零(力扣474) 求装满这个背包最多有多少个物品 给你一个二进制字符串数组 strs 和两个整数 m 和 n 。 请你找出并返回 strs 的最大子集…...
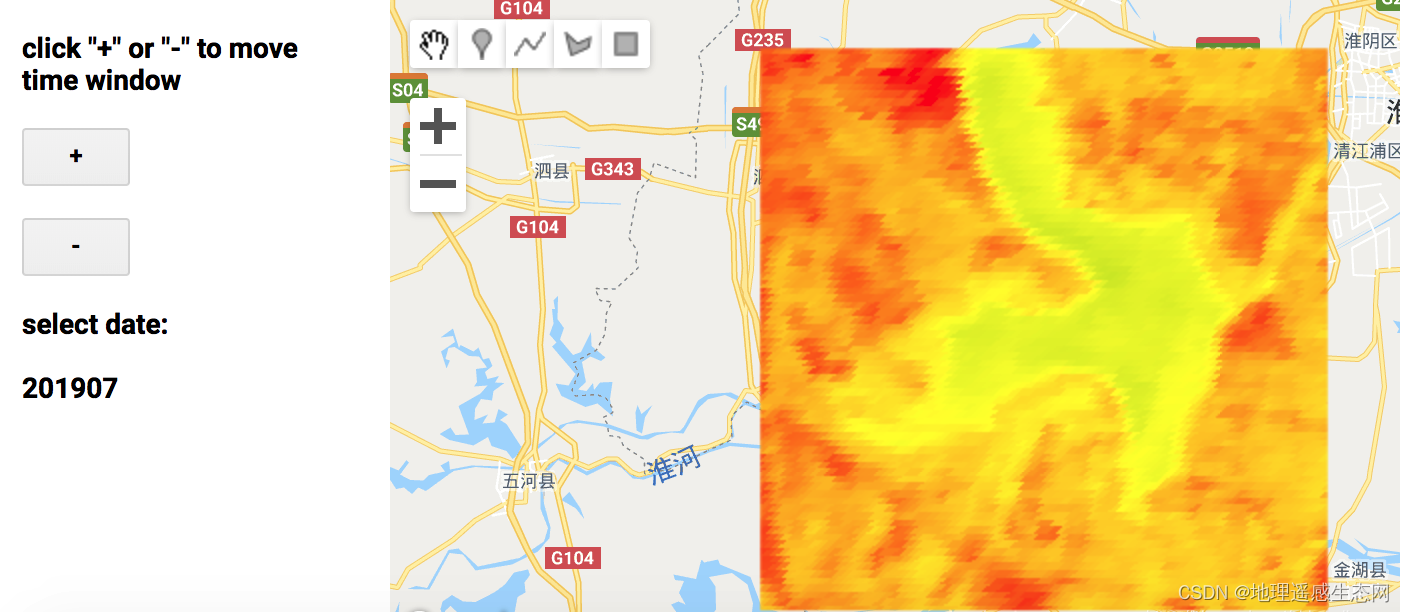
GEE学习笔记 七十八:干涸的洪泽湖
今天看了一篇报道直击60年一遇气象干旱:洪泽湖缩小近一半,鱼蟹受灾严重!_新华报业网(直击60年一遇气象干旱:洪泽湖缩小近一半,鱼蟹受灾严重!),既然玩GEE那就要玩出点花样…...

双指针【灵神基础精讲】
来源0x3f:https://space.bilibili.com/206214 文章目录同向双指针[209. 长度最小的子数组](https://leetcode.cn/problems/minimum-size-subarray-sum/)[713. 乘积小于 K 的子数组](https://leetcode.cn/problems/subarray-product-less-than-k/)[3. 无重复字符的最…...

tushare量化数据库模块怎么分析?
tushare量化数据其实包含的数据库有些是需要收费的,也有些会免费提供,不过tushare量化数据库整个库就很大很大,涉及的范围也广,挖掘这些数据还得从量化股票接口说起,就比如说在股票量化领域,tushare量化数据…...

模型转换 PyTorch转ONNX 入门
前言 本文主要介绍如何将PyTorch模型转换为ONNX模型,为后面的模型部署做准备。转换后的xxx.onnx模型,进行加载和测试。最后介绍使用Netron,可视化ONNX模型,看一下网络结构;查看使用了那些算子,以便开发部署…...
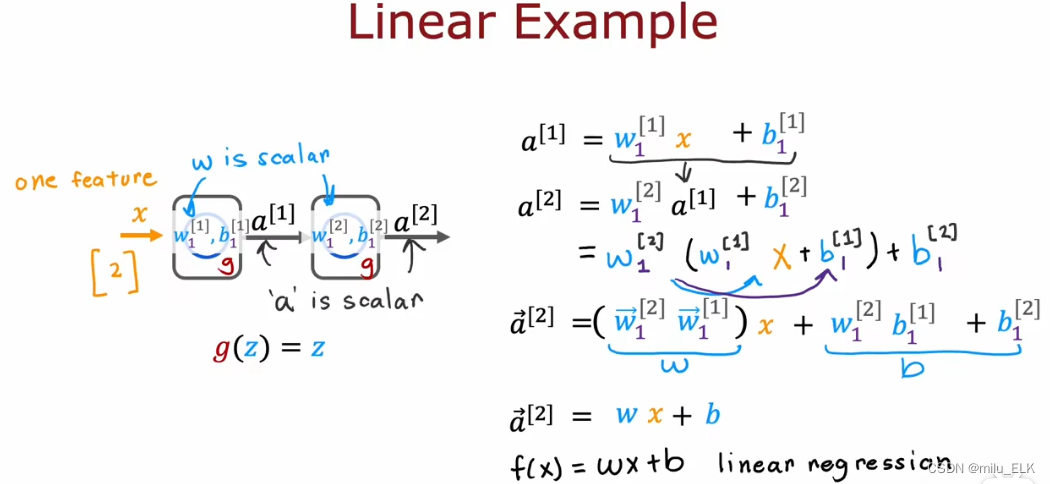
【深度学习】激活函数
上一章——认识神经网络 新课P54介绍了强人工智能概念,P55到P58解读了矩阵乘法在代码中的应用,P59,P60介绍了在Tensflow中实现神经网络的代码及细节,详细的内容可以自行观看2022吴恩达机器学习Deeplearning.ai课程,专…...
)
【新2023】华为OD机试 - 数字的排列(Python)
华为 OD 清单查看地址:blog.csdn.net/hihell/category_12199275.html 数字的排列 题目 小华是个很有对数字很敏感的小朋友, 他觉得数字的不同排列方式有特殊的美感。 某天,小华突发奇想,如果数字多行排列, 第一行1个数, 第二行2个, 第三行3个, 即第n行n个数字,并且…...

[oeasy]python0085_ASCII之父_Bemer_COBOL_数据交换网络
编码进化 回忆上次内容 上次 回顾了 字符编码的 进化过程 IBM 在数字化过程中 作用 非常大IBM 的 BCDIC 有 黑历史 😄 6-bit的 BCDIC 直接进化成 8-bit的 EBCDIC补全了 小写字母 和 控制字符 在ibm就是信息产业的年代 ibm的标准 怎么最终 没有成为 行业的标准 呢…...

volatile,内存屏障
volatile的特性可见性: 对于其他线程是可见,假设线程1修改了volatile修饰的变量,那么线程2是可见的,并且是线程安全的重排序: 由于CPU执行的时候,指令在后面的会先执行,在指令层级的时候我们晓得volatile的特性后,我们就要去volatile是如何实现的,这个很重要!&#…...

【ESP 保姆级教程】玩转emqx MQTT篇① —— 系统主题、延迟发布、服务器配置预算、常见问题
忘记过去,超越自己 ❤️ 博客主页 单片机菜鸟哥,一个野生非专业硬件IOT爱好者 ❤️❤️ 本篇创建记录 2023-02-18 ❤️❤️ 本篇更新记录 2023-02-18 ❤️🎉 欢迎关注 🔎点赞 👍收藏 ⭐️留言📝🙏 此博客均由博主单独编写,不存在任何商业团队运营,如发现错误,请…...
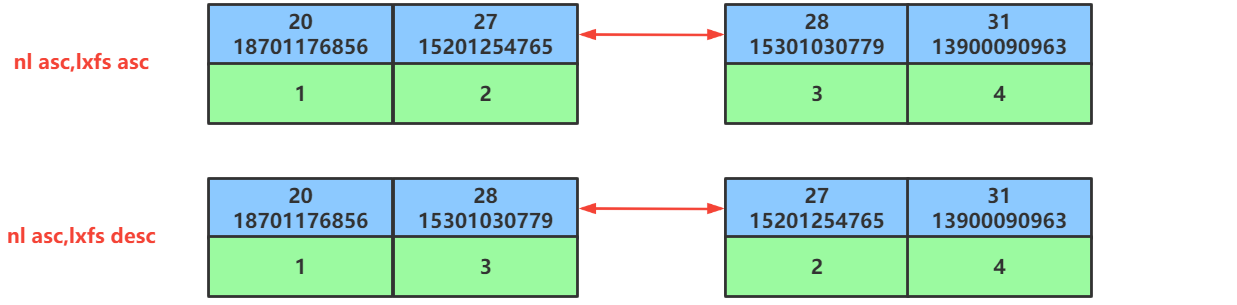
第48讲:SQL优化之ORDER BY排序查询的优化
文章目录1.ORDEY BY排序查询优化方面的概念2.ORDER BY排序的优化原则3.ORDER BY排序优化的案例3.1.准备排序优化的表以及索引3.2.同时对nl和lxfs字段使用升序排序3.3.同时对nl和lxfs字段使用降序排序3.4.排序时调整联合索引中字段的位置顺序3.5.排序时一个字段使用升序一个字段…...
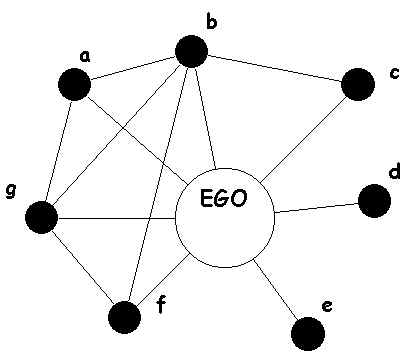
[Datawhale][CS224W]图机器学习(三)
目录一、简介与准备二、教程2.1 下载安装2.2 创建图2.2.1 常用图创建(自定义图创建)1.创建图对象2.添加图节点3.创建连接2.2.2 经典图结构1.全连接无向图2.全连接有向图3.环状图4.梯状图5.线性串珠图6.星状图7.轮辐图8.二项树2.2.3 栅格图1.二维矩形栅格…...

2023版最新最强大数据面试宝典
此套面试题来自于各大厂的真实面试题及常问的知识点,如果能理解吃透这些问题,你的大数据能力将会大大提升,进入大厂指日可待!目前已经更新到第4版,广受好评!复习大数据面试题,看这一套就够了&am…...

CSS 中的 BFC 是什么,有什么作用?
BFC,即“块级格式化上下文”(Block Formatting Context),是 CSS 中一个重要的概念,它指的是一个独立的渲染区域,让块级盒子在布局时遵循一些特定的规则。BFC 的存在使得我们可以更好地控制文档流࿰…...

总结在使用 Git 踩过的坑
问题一: 原因 git 有两种拉代码的方式,一个是 HTTP,另一个是 ssh。git 的 HTTP 底层是通过 curl 的。HTTP 底层基于 TCP,而 TCP 协议的实现是有缓冲区的。 所以这个报错大致意思就是说,连接已经关闭,但是此时有未处理…...

从 HTTP 到 gRPC:APISIX 中 etcd 操作的迁移之路
罗泽轩,API7.ai 技术专家/技术工程师,Apache APISIX PMC 成员。 原文链接 Apache APISIX 现有基于 HTTP 的 etcd 操作的局限性 etcd 在 2.x 版本的时候,对外暴露的是 HTTP 1 (以下简称 HTTP)的接口。etcd 升级到 3.x…...
【C语言每日一题】——倒置字符串
【C语言每日一题】——倒置字符串😎前言🙌倒置字符串🙌总结撒花💞😎博客昵称:博客小梦 😊最喜欢的座右铭:全神贯注的上吧!!! 😊作者简…...

Native扩展开发的一般流程(类似开发一个插件)
文章目录大致开发流程1、编写对应的java类服务2、将jar包放到对应位置3、配置文件中进行服务配置4、在代码中调用5、如何查看服务调用成功大致开发流程 1、编写服务,打包为jar包2、将jar包放到指定的位置3、在配置文件中进行配置,调用对应的服务 1、编…...

【新解法】华为OD机试 - 任务调度 | 备考思路,刷题要点,答疑,od Base 提供
华为 OD 清单查看地址:blog.csdn.net/hihell/category_12199275.html 任务调度 题目 现有一个 CPU 和一些任务需要处理,已提前获知每个任务的任务 ID、优先级、所需执行时间和到达时间。 CPU 同时只能运行一个任务,请编写一个任务调度程序,采用“可抢占优先权调度”调度…...
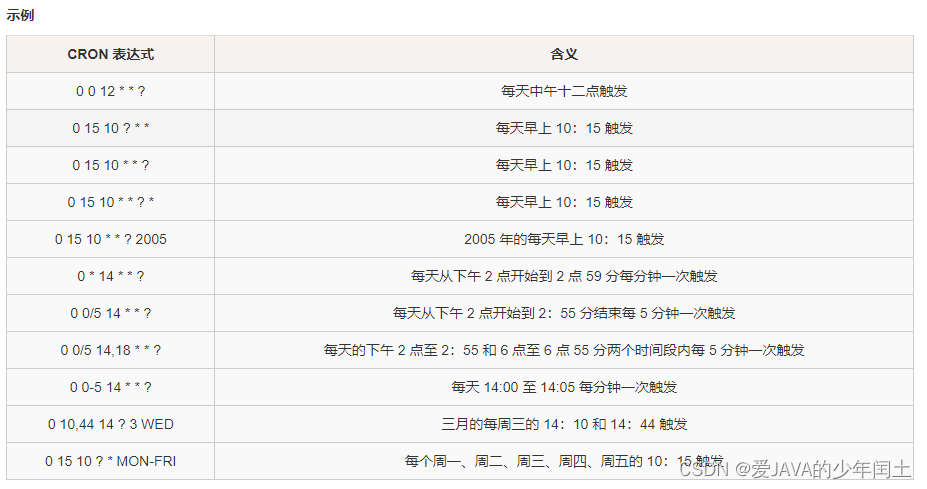
Spring3定时任务
简介 Spring 内部有一个 task 是 Spring 自带的一个设定时间自动任务调度,提供了两种方式进行配置,一种是注解的方式,而另外一种就是 XML 配置方式了;注解方式比较简洁,XML 配置方式相对而言有些繁琐,但是应用场景的不…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...
