计算机组成原理学习笔记:循环冗余校验码
循环冗余校验码 CRC 码
- 循环冗余校验码 (cyclic redundancy Check, CRC)
十进制除法
- 从熟悉的十进制出发,假设现在你要给另一个人传送882这样的一个10进制数据,为了防止传送数据的过程中某一个数据发生错误
- 你可以和你的另一个小伙伴约定一个除数,比如:7, 882÷7刚好是除的尽的,最后我们算得的余数是等于0
- 当数据的接收方接收到数据的时候,就可以用它接收到的这个数据和你们约定的这个除数进行一个除法操作
- 检查余数是否为0,如果余数不等于0,那么是不是就可以确定数据传输的过程中肯定是发生了错误
- 比如说对方收到的其实是883,也就是最后一个数发生了错误,那883÷7,最后可以算的余数=1,不等于0
- 那么这就说明肯定是发生了错误,需要重新传送,再比如,第2个数据发生了错误, 由8变成5(即:852),那么除以7得到的余数是等于5
- 同样,这种情况也可以确定,我们的数据传输肯定出现了问题,这是我们熟悉的十进制除法
- 总结一下:
- 我们通过约定一个除数,然后在接收到数据之后与这个除数进行相除的操作
- 检查余数是否发生了改变, 用这样的方式就可以检测出数据传送的错误
基本思想
- 其实,CRC的思想和十进制除法的思想是类似的
- 就是数据的发送方和接收方会先约定一个除数
- 当然了我们处理的是计算机里面的数据, 所以这个数肯定是一个二进制的数
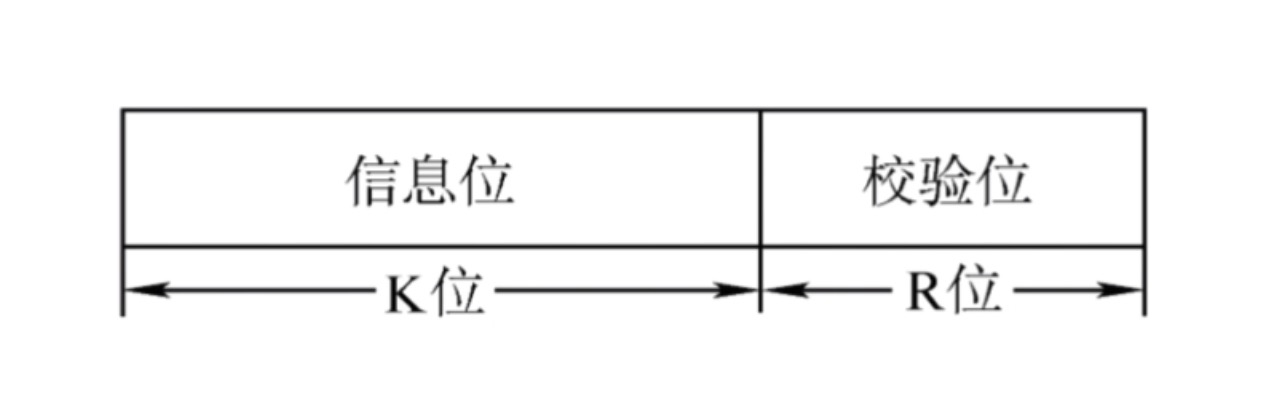
- 然后我们会想办法在K个原始的信息位后面加上R个校验位,我们需要确保拼接上这R个校验位之后,
- 这一整串的数据和我们刚才约定的除数进行相除的操作,余数要等于0
- 接下来数据的接收方接收到这 K+R 位的数据之后,需要用二进制除法来检查余数是否等于0
- 如果余数不等于0,那么就说明有一些二进制位出现了错误,那这种情况下我们就可以进行重传
- 或者某些时候也可以进行单比特位的纠错,这就是循环冗余校验码的一个思想
如何检错纠错
检错
- 构建循环冗余校验码需要有这样的两个关键的要素:一个是除数,一个是被除数
- 一般来说试题中会用这种生成多项式的方式给出除数,比如例题如下:
- 设生成多项式为 G(x)=x3+x2+1G(x)=x^3+x^2+1G(x)=x3+x2+1, 信息码为101001,求对应的CRC码
- 其实这题可以描述为:1∗x3+1∗x2+0∗x1+1∗x01 * x^3 + 1 * x^2 + 0 * x^1 + 1 * x^01∗x3+1∗x2+0∗x1+1∗x0
- 可见,在这个生成多项式中,这些项的系数,要么为1,要么为0
- 因此我们可以把这个生成多项式转换成对应的二进制数, 即:1101
- 这一题的核心在于:确定K、R以及生成多项式对应的二进制码,一般而言,
- K = 信息码的长度
- R = 生成多项式最高次幂,在这里题目中是3
- 这样的话:校验码位数 N = K + R = 6 + 3 = 9
- 由上面的换算可知,我们的二进制码有4个比特,也即是:1101
- 思路:6位信息位+3个校验位生成的9位校验码,除以对应的二进制码,所得余数要为0
- 因此接下来我们需要确定的是添加的这三位校验位应该是多少才能保证余数为零,做法是这样的
- 把信息码左移R位,也即是3位,即:101001000
- 接下来就是相除的操作:101001000 / 1101, 这个除法会让我们得到R位的余数,也就是3位余数
- 不过这个地方我们需要进行的是模2除的运算和我们普通的除法是有一些区别的, 后续来说明
注意体会:模2除和模2减

- 首先由于除数有4位,所以我们会取被除数的高四位与他先商一次,模2除里取商的方式比较特别
- 我们只看当前我们划出来的最高位,如果它是1,那么我们就商 1,那1×1001=1001,我们把它填到下面
- 接下来我们会对后三位进行模2减的运算,其实模2减的效果和模2加是相同的,模2加其实就是异或运算
- 所以事实上我们就是对后边的三位进行了异或运算,先看0和1异或等于1,1和0异或等于1,0和1异或同样等于1
- 因此后边三位进行模2减或者说分别进行异或得到的结果是111
- 接下来有点类似于十进制除法,我们把被除数的后面一位补到刚才得到的这个余数的低位, 得到 1110
- 然后,我们要确定下一位的商,和之前一样,我们只看最高位,如果最高位为1的话,那我们就商1,
- 同样的: 1 × 1101 = 1101, 接下来我们需要对后面的三位进行一次模2减的运算
- 那1和1进行模二减就相当于它们俩进行了一次异或等于0,1和0异或等于1,0和1异或等于1
- 所以这次模2减得到的是011,接下来再补一位,凑足四位,现在由于这儿的高位为0,所以接下来我们应该商0,
- 那么0 × 1100 = 0000,所以我们在下边写上4个0,接下来同样的我们需要把后三位进行模2减或者说异或的运算得到三个1
- 现在由于高位是1,所以下一个商,我们应该商1,得到1101,后三位进行模2减得到011,再补一个0,现在由于高位是0,所以我们需要商0
- 因此接下来需要减0000,后三位进行模2减,得到110,最后还剩一个0,我们在把它补上去
- 由于此时高位为1,所以我们要上商1,那么和1101的后三位进行模2减,得到的结果是001
- 那001就是我们刚才的这一串代码和1101进行模2除得到的一个余数
- 用模2除的规则,最终得到的余数位数应该只比这个除数少一位,那我们用这些操作得到的余数就是我们的校验位
- 所以最终我们得到的CRC校验码就应该是:前6个信息位101001再拼上最后的校验位001,即:101001001,这就是校验位的一个确定方式
- 用这种方式确定的校验码和1101进行模2除,得到的余数一定是000
- 现在我们已经有了校验码,那么我们就可以把一整串的信息进行传输发送,接收方接收到数据之后就需要进行检错和纠错
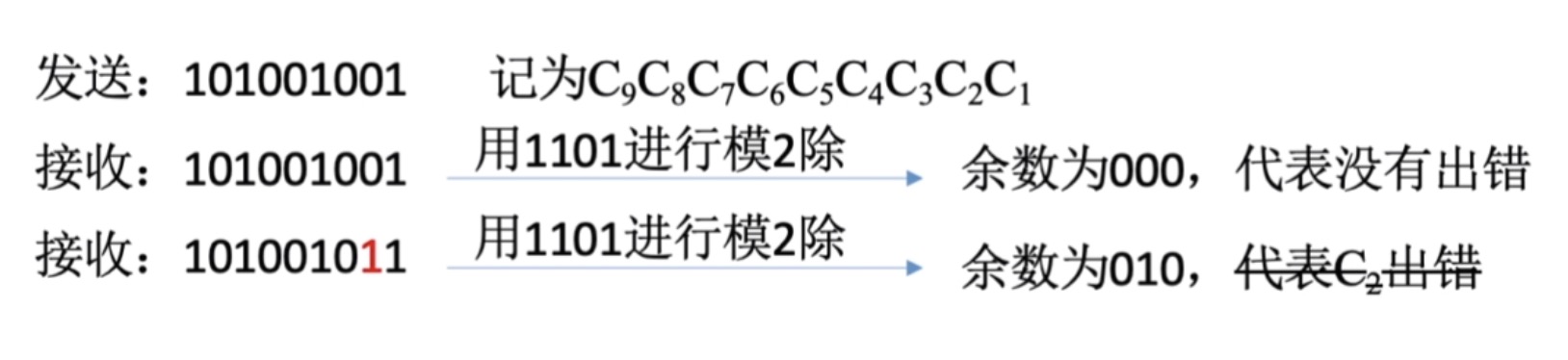
- 注意发送方和接收方提前已经约定好了生成多项式或者说约定好了除数,当接收方接收到数据之后,就可以用接收到的这一串信息和刚才约定好的这个除数进行模二除的运算
- 如果最终得到的余数是000。那么就代表没有出错
- 注意上图接收出错的地方,最终得到的余数应该是010,这里会发现一个巧合,我们得到的这个余数如果把它翻译成十进制的话,刚好就是2
- 而出错的位置刚好也是C2C_2C2这个位置,但其实这语速和出错位置之间并没有这样必然的联系
- 把原始的这一串数据各个位置进行了一个改变,如果出错位在第1位的话,那么和这个生成多项式进行,模2除得到的余数是001
- 如果是第2位, 那得到余数是010, 如果出错的位置是第3位,那得到的余数是100,如果把100翻译成十进制的话,是等于4
- 所以这个余数的值和出错位置之间,其实并不是二进制到十进制的转换这么简单
- 但是余数和出错位置确实又有对应关系,我们会发现这儿的余数只有三个bit的信息,而3个bit的信息总共只能表示2的三次方,也就是8种状态
- 如果余数等于三个0,那么表示这个数据的传输是正确的,接下来出错位为1234567这7种状况分别会对应不同的余数
- 那这7种余数再加上000, 已经把3个bit能够表示的信息都表示了,所以我们再看如果第8位出错的话,余数又会等于001
- 然后如果是第9位出错的话,余数又等于010,也就相当于这个余数又从头来了一遍,第1个是001,第2个是010
- 所以如果余数等于010就可以确定是第2位出错了吗?这个结论显然是站不住脚的,因为第9位出错也有可能会导致余数变为010
- 因此刚才那句话我们划了一条横线,表示他并不严谨,并不正确
纠错
- 那既然如此是不是意味着循环冗余校验吗?它只有检测的能力,而没有纠错的能力,也就是无法确定出错的位置在哪,这种理解也不全对
- 像刚才这个例子当中,由于我们信息位加校验位,总共有9位,而校验码只有3位的信息,3位的信息最多只能表示8种状态
- 无法完全的标注出这9个位置, 到底是哪一个位置发生了错误,所以并不是循环冗余校验码没有纠错的能力,而是这个例子当中信息位太长了
- 所以我们再看另一个例子, 如果信息位只有4位,然后生成多项式和之前是一样的,除数1101,如下
- 信息位:0100
- 生成多项式:G(x)=x3+x2+1(1101)G(x)=x^3+x^2+1 \quad (1101)G(x)=x3+x2+1(1101)
- 首先我们的信息为后面补三个0,得到 0100000, 然后用这一整串对1101进行模2除运算,得到余数011
- 所以最终得到的CRC码就应该是这4个信息位再拼接上011这三个校验位,即:0100011
- 接下来如果这串数据传输过程中没有任何一位发生错误, 那显然余数应该是等于零
- 如果发生错误了,如下表所示:
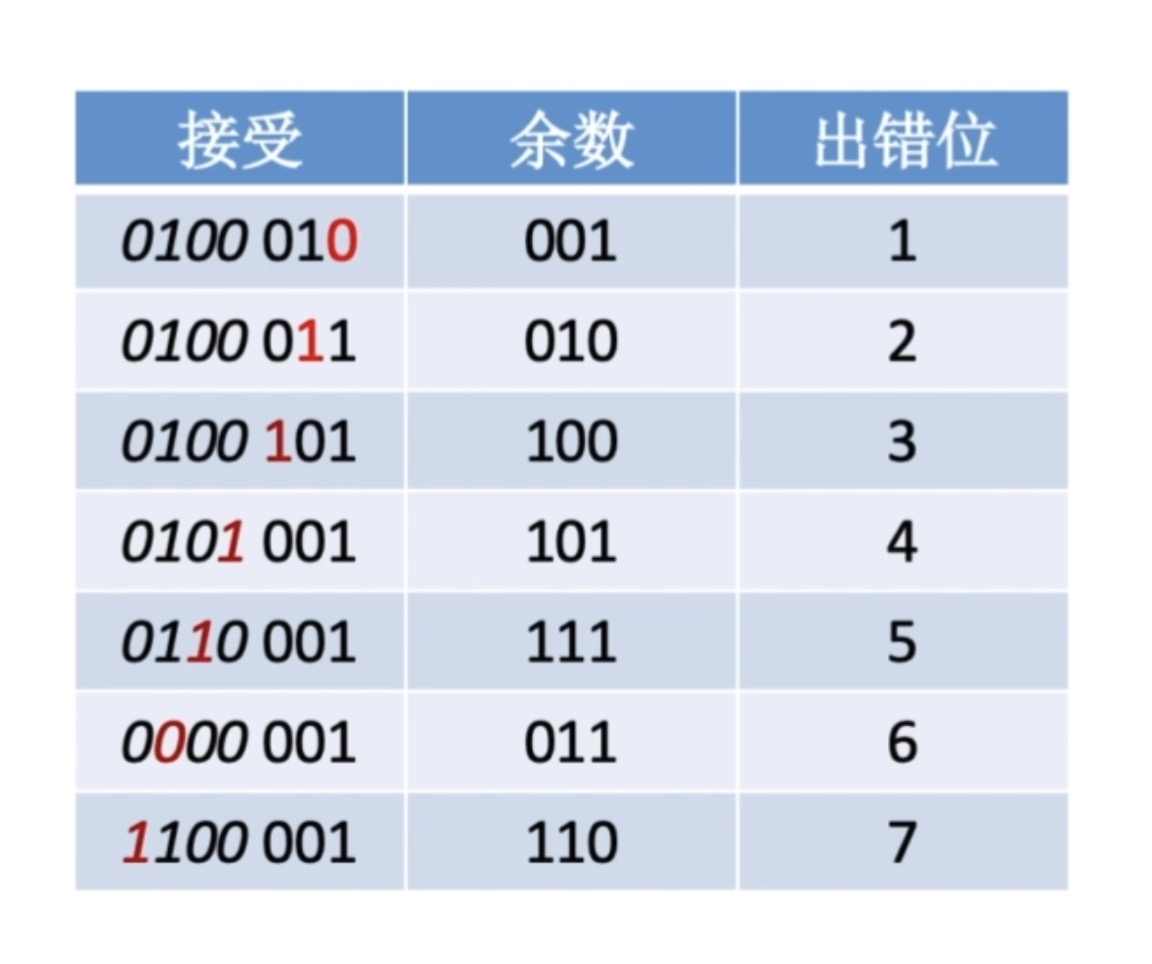
- 如果第1位发生错误,那余数是001,如果是第2位发生错误余数是010,第3位是100,…
- 同样,余数和出错位置之间的这个对应关系与上一个例子当中,并没有发生任何改变
- 所以这也就意味着只要我们确定了一个生成多项式,无论我们的信息位如何变化,最终这个余数的值和出错位置之间,肯定都是一种固定不变的对应关系
- 而如果数据的位数并没有超过余数所能表示的这个范围,那么余数和出错位之间就是一一对应的关系
- 在这个例子当中,如果余数等于010,那我们就可以确定出错的一定是第2位,于是我们只需要纠正第2位就可以了
- 所以循环冗余校验码其实是有纠错功能的,只不过信息位的位数不能太多,那到底要多少个信息问才不算多呢,这儿给出了一个不等式
- 2R≥K+R+12^R \ge K + R + 12R≥K+R+1
- 这个和海明码的不等式是很类似的,我们有R个校验位,就意味着最终我们会得到R位的余数,而这么多位的余数可以表示2的R次方这么多种状态
- 其中有一种状态,也就是余数为000,这种状态是对应正确的状态,然后剩下的2R−12^R-12R−1这么多种状态需要分别对应上K+R这么多位,每一位出现错误的那种情况,需要进行一一对应
- 所以如果能够满足 2R≥K+R+12^R \ge K + R + 12R≥K+R+1 ,那么CRC校验码就拥有可以纠正一位错误的能力,不过在实际应用当中,CRC码这种方式通常用于计算机网络的数据传输
- 通常会把几千个比特的信息位加上几个校验位,所以在实际使用当中,这种校验码通常只会用来检错,而不会用于纠错,我们需要知道的是它实际上是有纠错能力的
- 理论上这种校验码它可以检测出所有的奇数个错误,同时可以检测出所有的双比特错误,另外它可以检测出小于等于校验位长度,也就是小于等于R位的连续的错误
总结
- 循环冗余校验码
- 构造
- 由生成多项式确定"除数",若生成多项式中x的最高次为R,则"除数"有R+1位
- K个信息位 + R个0,作为"被除数"
- 被除数、除数进行"模二除",得R位余数
- K个信息位+R位余数 = CRC码
- 校验
- 收到K+R位数据,与生成多项式模2除,计算R位余数
- 余数为0,说明无错误
- 余数非0,说明出错
- 检错、纠错能力
- 可检测出所有奇数个错误
- 可检测出所有双比特的错误
- 可检测出所有小于等于校验位长度的连续错误
- 若选择合适的生成多项式,且 2R≥K+R+12^R \ge K + R + 12R≥K+R+1,则可纠正单比特错
- 构造
相关文章:

计算机组成原理学习笔记:循环冗余校验码
循环冗余校验码 CRC 码 循环冗余校验码 (cyclic redundancy Check, CRC) 十进制除法 从熟悉的十进制出发,假设现在你要给另一个人传送882这样的一个10进制数据,为了防止传送数据的过程中某一个数据发生错误你可以和你的另一个小伙伴约定一个除数&…...
 A — C)
Educational Codeforces Round 143 (Rated for Div. 2) A — C
Educational Codeforces Round 143 (Rated for Div. 2) 文章目录A. Two Towers题目大意题目分析codeB. Ideal Point题目大意题目分析codeC. Tea Tasting题目大意题目分析codeA. Two Towers 题目大意 有两个有红蓝两种颜色组成的塔,每次操作可以将其中一个塔顶的色…...
【Unity VR开发】结合VRTK4.0:将浮点数从交互器传递到可交互对象
语录: 愿你熬得过万丈孤独,藏得下星辰大海。 前言: 默认情况下,交互器只能将单个布尔操作传递给可交互对象,后者控制可交互对象上的抓取操作。在其他时候,交互器中的其他操作可能希望传递给可交互对象&…...
)
【图像分类】基于PyTorch搭建卷积神经网络实现MNIST手写数字识别(附项目完整代码)
写在前面: 首先感谢兄弟们的关注和订阅,让我有创作的动力,在创作过程我会尽最大能力,保证作品的质量,如果有问题,可以私信我,让我们携手共进,共创辉煌。 在【图像分类】基于PyTorch搭建LSTM实现MNIST手写数字体识别(单向LSTM,附完整代码和数据集)文章中,我们使用了…...
4.4 MQC
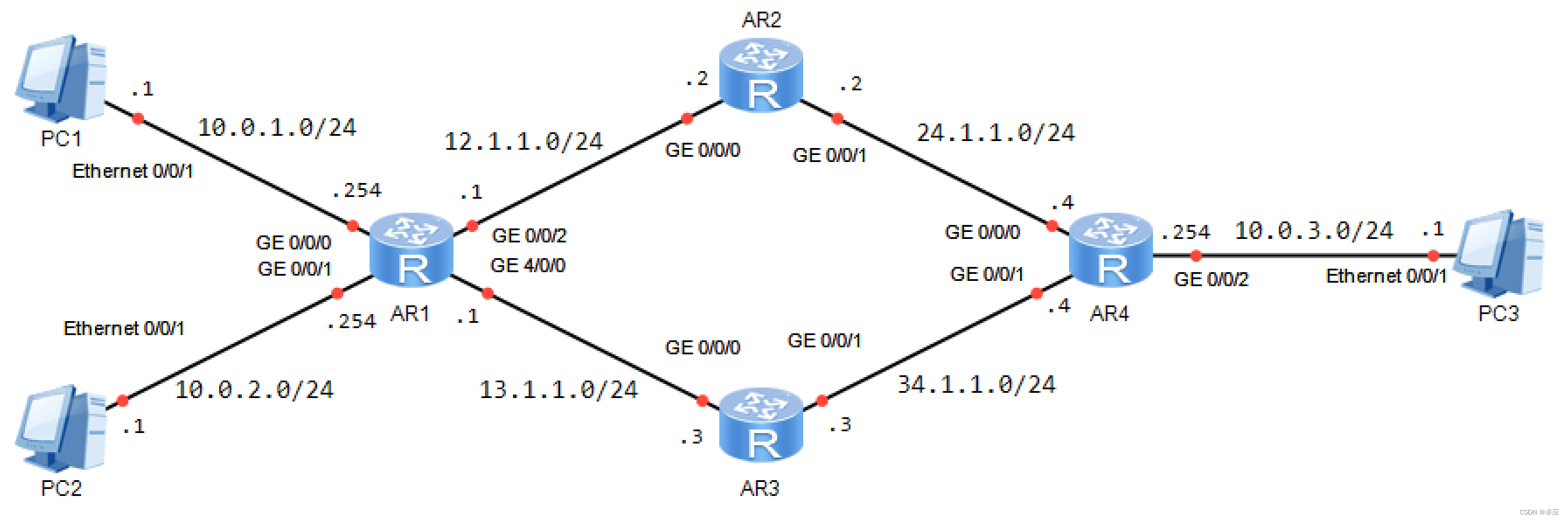
1. 实验目的 熟悉MQC的应用场景掌握MQC的配置方法2. 实验拓扑 实验拓扑如图4-10所示: 图4-10:MQC 3. 实验步骤 (1) IP地址的配置 AR1的配置 <Huawei>system-view...
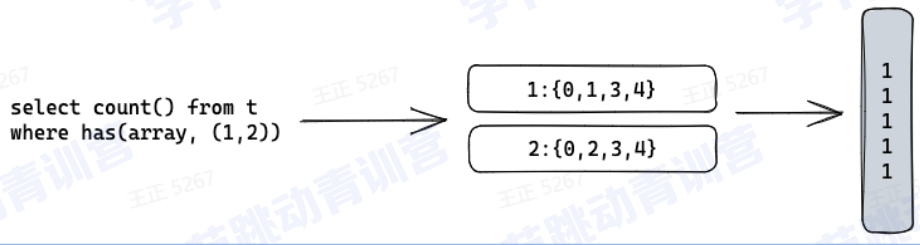
ClickHouse列存储(十一)—— ClickHouse
文章目录一、重点内容:1.数据库基本概念2.列式存储3.clickHouse存储设计4.clickHouse典型应用场景二、准备工作:1、了解数据库基本概念2、了解列式存储相关概念3、了解ClickHouse存储设计4、了解 ClickHouse典型应用场景三、详细知识点介绍:1…...

公司来了个卷王,真让人奔溃
2022年已经结束结束了,最近内卷严重,各种跳槽裁员,相信很多小伙伴也在准备今年的金三银四的面试计划。 在此展示一套学习笔记 / 面试手册,年后跳槽的朋友可以好好刷一刷,还是挺有必要的,它几乎涵盖了所有的…...
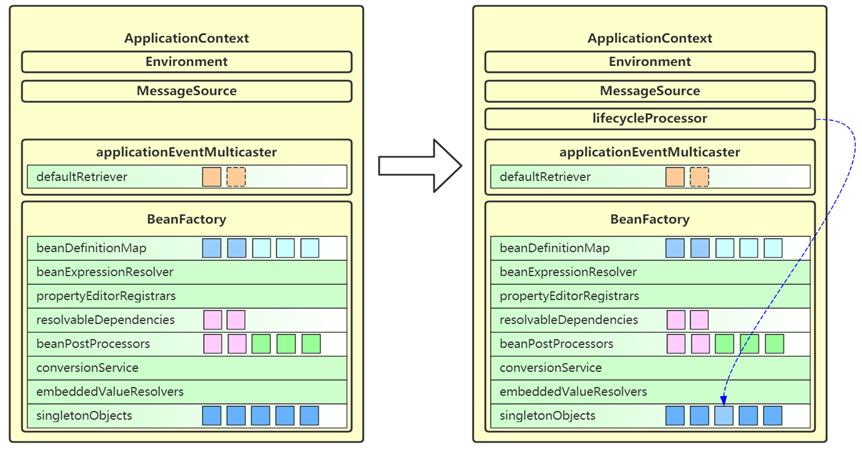
什么是refresh?Spring refresh 流程
refresh 是 AbstractApplicationContext 中的一个方法,负责初始化 ApplicationContext 容器,容器必须调用 refresh 才能正常工作。它的内部主要会调用 12 个方法,我们把它们称为 refresh 的 12 个步骤:1. prepareRefresh2. obtain…...
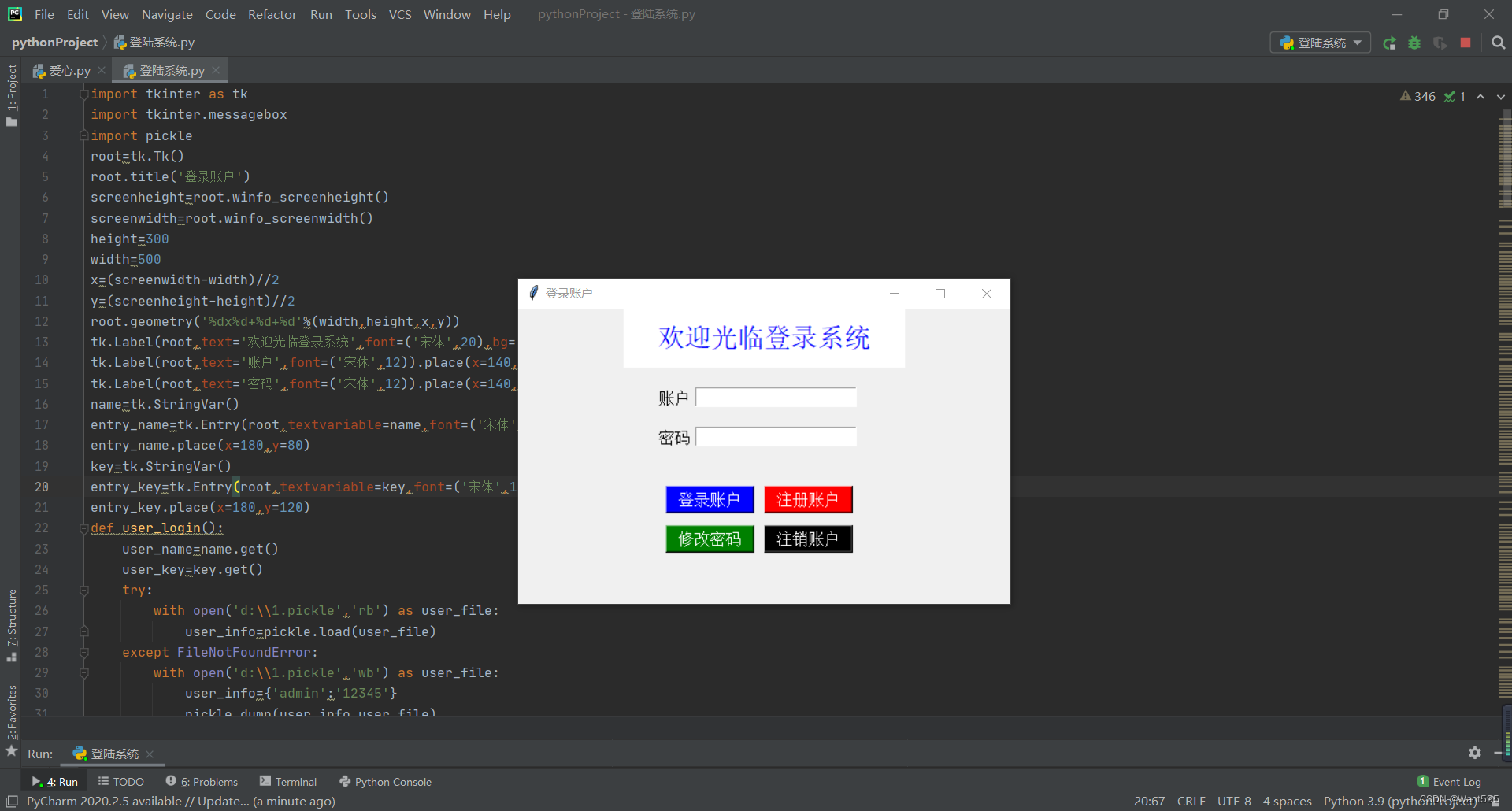
Python登陆系统
前言 #源码见文末公众号哈# 登录系统 一个简单的登录系统包含了登录账户、注册账户、修改密码以及注销账户的操作。 1. 登录账户 登录系统主要需要判断账户是否存在,不存在就注册一个账户,如果第一次登录系统,我们需要先新建一个文件&…...
)
【新2023】华为OD机试 - 重组字符串(Python)
华为 OD 清单查看地址:blog.csdn.net/hihell/category_12199275.html 重组字符串 题目 给定一个非空字符串 S,其被 N 个‘-’分隔成 N+1 的子串,给定正整数 K, 要求除第一个子串外,其余的子串每 K 个字符组成新的子串,并用‘-’分隔。 对于新组成的每一个子串,如果它…...

视频监控流程图
<html> <head> <meta http-equiv"Content-Type" content"text/html; charsetUTF-8"/> <link rel"stylesheet" type"text/css" href"visio.css"/> <title> 视频监控流程图 </title> <…...

普通单双面板的生产工艺流程之图形转移,华秋一文告诉你
衔接上文,继续为朋友们分享普通单双面板的生产工艺流程。 如图,第五道主流程为图形转移。 图形转移的目的为: 利用光化学原理,将图形线路的形状转移到印制板上,再利用化学原理,将图形线路在印制板上制作出…...

1.8 providers
生成providersnest g service <name>providers的注入方式构造函数注入Injectable() export class KeywordService {constructor(private readonly httpService: HttpService,private readonly pro: ProService,) {} }Inject()注入export class KeywordController {Inject…...
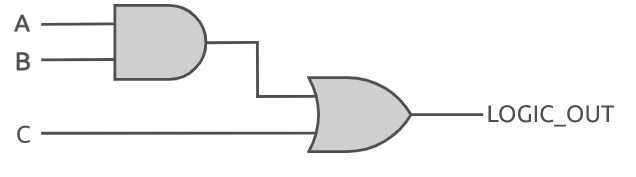
如何编写一个基本的 Verilog Module(模块)
1、概述这篇文章主要介绍了 Verilog 在 FPGA 设计中的概念和使用方法。首先讨论使用模块(module)关键字构造 Verilog 设计的方式,以及这与所描述的硬件的关系。这包括对参数、端口(port)和例化(instantiato…...

让乔布斯想要「发动核战争」的 Android,为何成了占有率最高的系统?
2008 年 9 月 23 日,Apple 的创始人和 CEO 史蒂夫乔布斯像往常一样走进了公司,此时距离初代 iPhone 的发布会才过了一年半,这款充满了争议的产品就像一块从山崖滚落的巨岩,一路电光石火的给手机市场的《小石潭记》来了场焚书坑儒。…...

FPGA开发软件(vivado + modelsim)环境搭建(附详细安装步骤+软件下载)
本文详细介绍了vivado软件和modelsim软件的安装,以及vivado中配置modelsim仿真设置,每一步都加文字说明和图片。一、软件安装包下载1、vivado vivado版本很多,目前最新的已更新到vivado2022.2,版本越高,安装包越大&…...

TypeScript 学习之类型
布尔类型 类型: boolean最简单的类型,值只有 true/false let isDone: boolean true;数字类型 类型:number数字都是浮点数,支持二进制、八进制、十进制、十六进制。 let decLiteral: number 16; // 十进制 let hexLiteral: number 0xf0…...

基于MATLAB计算MIMO信道容量(附完整代码与分析)
目录 一.介绍 二. 代码 三. 运行结果及分析 3.1 MIMO信道容量:固定发射天线数为4 3.2 MIMO信道容量:固定接收天线数为4 3.3 AWGN信道与瑞利信道容量 四. 总结 一.介绍 本文章将在MATLAB环境中分析MIMO信道容量,AWGN信道容量…...

CSDN城市开发者联盟、C友会期待你的加入
文章目录🌟 课前小差🌟 chatGPT🌟 CSDN中的持续学习🌟 23年原力计划🌟 C友会、CDC🌟 如何关联本地的开发者?🌟 写在最后🌟 课前小差 哈喽,大家好,…...
)
【新2023】华为OD机试 - 吃火锅(Python)
华为 OD 清单查看地址:blog.csdn.net/hihell/category_12199275.html 吃火锅 题目 入职后,导师会请你吃饭,你选择了火锅, 火锅里会在不同时间下很多菜, 不同食材要煮不同时间,才能变得刚好合适, 你希望吃到最多的刚好合适的菜, 但是你的手速不够快用m代替手速, 每次…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

c# 局部函数 定义、功能与示例
C# 局部函数:定义、功能与示例 1. 定义与功能 局部函数(Local Function)是嵌套在另一个方法内部的私有方法,仅在包含它的方法内可见。 • 作用:封装仅用于当前方法的逻辑,避免污染类作用域,提升…...

云原生周刊:k0s 成为 CNCF 沙箱项目
开源项目推荐 HAMi HAMi(原名 k8s‑vGPU‑scheduler)是一款 CNCF Sandbox 级别的开源 K8s 中间件,通过虚拟化 GPU/NPU 等异构设备并支持内存、计算核心时间片隔离及共享调度,为容器提供统一接口,实现细粒度资源配额…...

高考志愿填报管理系统---开发介绍
高考志愿填报管理系统是一款专为教育机构、学校和教师设计的学生信息管理和志愿填报辅助平台。系统基于Django框架开发,采用现代化的Web技术,为教育工作者提供高效、安全、便捷的学生管理解决方案。 ## 📋 系统概述 ### 🎯 系统定…...
之(六) ——通用对象池总结(核心))
怎么开发一个网络协议模块(C语言框架)之(六) ——通用对象池总结(核心)
+---------------------------+ | operEntryTbl[] | ← 操作对象池 (对象数组) +---------------------------+ | 0 | 1 | 2 | ... | N-1 | +---------------------------+↓ 初始化时全部加入 +------------------------+ +-------------------------+ | …...

React父子组件通信:Props怎么用?如何从父组件向子组件传递数据?
系列回顾: 在上一篇《React核心概念:State是什么?》中,我们学习了如何使用useState让一个组件拥有自己的内部数据(State),并通过一个计数器案例,实现了组件的自我更新。这很棒&#…...

在MobaXterm 打开图形工具firefox
目录 1.安装 X 服务器软件 2.服务器端配置 3.客户端配置 4.安装并打开 Firefox 1.安装 X 服务器软件 Centos系统 # CentOS/RHEL 7 及之前(YUM) sudo yum install xorg-x11-server-Xorg xorg-x11-xinit xorg-x11-utils mesa-libEGL mesa-libGL mesa-…...

第6章:Neo4j数据导入与导出
在实际应用中,数据的导入与导出是使用Neo4j的重要环节。无论是初始数据加载、系统迁移还是数据备份,都需要高效可靠的数据传输机制。本章将详细介绍Neo4j中的各种数据导入与导出方法,帮助读者掌握不同场景下的最佳实践。 6.1 数据导入策略 …...
