普通单双面板的生产工艺流程之图形转移,华秋一文告诉你
衔接上文,继续为朋友们分享普通单双面板的生产工艺流程。
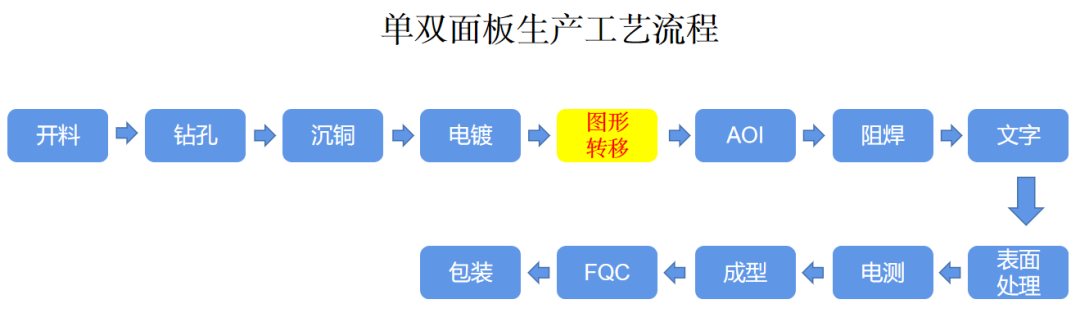
如图,第五道主流程为图形转移。
图形转移的目的为:
利用光化学原理,将图形线路的形状转移到印制板上,再利用化学原理,将图形线路在印制板上制作出来。
在行业内,普通单双面板的图形转移通常采用负片工艺。
在此,以干法的负片工艺为例,为朋友们进行讲述,其子流程,通常为4个。
【1】图形前处理(磨板)
在制作线路前,磨板,保证贴膜前的板面干燥、清洁、无氧化、胶渍等。

【2】干膜(压干膜/贴膜/贴干膜)
通过压膜机,在铜面上,贴附感光材料(干膜)。

【3】曝光
利用感光照相原理,使感光材料(干膜)受到紫外光照射(即曝光)后,发生聚合反应,完成图形转移。

注:曝光又为图形转移主流程中最重要的子流程,因此,相应的曝光设备也极为重要,业内通常会以作业方式进行区分,把曝光机分为:手动曝光机、全自动曝光机、LDI曝光机。

附注:通常情况下,在曝光精度方面,LDI曝光机>全自动曝光机>手动曝光机。因此,为了确保制作线路的精度,行业内的头部大厂,大多会购置LDI曝光机,华秋也是因此购买了LDI曝光机。
【4】DES(显影、蚀刻、退膜)
经过显影、蚀刻、退膜,去除掉不需要的干膜与铜箔,制作出所需要的图形线路。

如上,朋友们可能会觉得图形转移工序,其实也并不复杂,相比鄙人上篇对于电镀的分享,本文确实显得简单,但实际上,图形转移,是PCB生产工艺中最复杂、最重要的部分。
例如:
- 图形转移,可以根据菲林与所制作的图形线路是否一致,区分为正片、负片……(一致为正片,不一致为负片)
- 图形转移,可以根据所采用感光材料的不同,分为干法工艺、湿法工艺……(干膜为干法工艺,油墨为湿法工艺)
- 图形转移 ,还可以根据所采用蚀刻药水的不同,而区分出不同的药水体系……(关于蚀刻药水,目前行业内主要有6种:氯化铁、酸性氯化铜、碱性氯化铜、过硫酸铵、硫酸/铬酸、硫酸/双氧水蚀刻液)
本文之所以相对简单,并不是因为此工序简单,而是此工序过于复杂,鄙人的技术积淀尚且不够,是故无法为朋友们再进行更为全面的深入浅出的讲解。
假如朋友们还有深入学习的兴趣,建议查阅相关的文献资料或购买相关的专业书籍。
相关文章:

普通单双面板的生产工艺流程之图形转移,华秋一文告诉你
衔接上文,继续为朋友们分享普通单双面板的生产工艺流程。 如图,第五道主流程为图形转移。 图形转移的目的为: 利用光化学原理,将图形线路的形状转移到印制板上,再利用化学原理,将图形线路在印制板上制作出…...

1.8 providers
生成providersnest g service <name>providers的注入方式构造函数注入Injectable() export class KeywordService {constructor(private readonly httpService: HttpService,private readonly pro: ProService,) {} }Inject()注入export class KeywordController {Inject…...
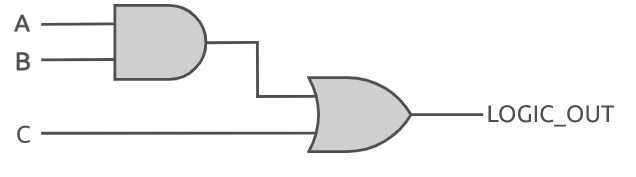
如何编写一个基本的 Verilog Module(模块)
1、概述这篇文章主要介绍了 Verilog 在 FPGA 设计中的概念和使用方法。首先讨论使用模块(module)关键字构造 Verilog 设计的方式,以及这与所描述的硬件的关系。这包括对参数、端口(port)和例化(instantiato…...

让乔布斯想要「发动核战争」的 Android,为何成了占有率最高的系统?
2008 年 9 月 23 日,Apple 的创始人和 CEO 史蒂夫乔布斯像往常一样走进了公司,此时距离初代 iPhone 的发布会才过了一年半,这款充满了争议的产品就像一块从山崖滚落的巨岩,一路电光石火的给手机市场的《小石潭记》来了场焚书坑儒。…...

FPGA开发软件(vivado + modelsim)环境搭建(附详细安装步骤+软件下载)
本文详细介绍了vivado软件和modelsim软件的安装,以及vivado中配置modelsim仿真设置,每一步都加文字说明和图片。一、软件安装包下载1、vivado vivado版本很多,目前最新的已更新到vivado2022.2,版本越高,安装包越大&…...

TypeScript 学习之类型
布尔类型 类型: boolean最简单的类型,值只有 true/false let isDone: boolean true;数字类型 类型:number数字都是浮点数,支持二进制、八进制、十进制、十六进制。 let decLiteral: number 16; // 十进制 let hexLiteral: number 0xf0…...

基于MATLAB计算MIMO信道容量(附完整代码与分析)
目录 一.介绍 二. 代码 三. 运行结果及分析 3.1 MIMO信道容量:固定发射天线数为4 3.2 MIMO信道容量:固定接收天线数为4 3.3 AWGN信道与瑞利信道容量 四. 总结 一.介绍 本文章将在MATLAB环境中分析MIMO信道容量,AWGN信道容量…...

CSDN城市开发者联盟、C友会期待你的加入
文章目录🌟 课前小差🌟 chatGPT🌟 CSDN中的持续学习🌟 23年原力计划🌟 C友会、CDC🌟 如何关联本地的开发者?🌟 写在最后🌟 课前小差 哈喽,大家好,…...
)
【新2023】华为OD机试 - 吃火锅(Python)
华为 OD 清单查看地址:blog.csdn.net/hihell/category_12199275.html 吃火锅 题目 入职后,导师会请你吃饭,你选择了火锅, 火锅里会在不同时间下很多菜, 不同食材要煮不同时间,才能变得刚好合适, 你希望吃到最多的刚好合适的菜, 但是你的手速不够快用m代替手速, 每次…...
类似LeetCode的登录页面(小程序版)
前言每一个项目都会有用户端的注册和登录页面,对于刚入门的小白来说,在UI设计方面不太擅长,就算大致的UI界面设计出来了,但是落实到代码上来实现的时候就很容易卡住。这篇博客主要介绍的就是仿作一个类似LeetCode登录的简约大方页…...

CUDA的统一内存
CUDA的统一内存 文章目录CUDA的统一内存N.1. Unified Memory IntroductionN.1.1. System RequirementsN.1.2. Simplifying GPU ProgrammingN.1.3. Data Migration and CoherencyN.1.4. GPU Memory OversubscriptionN.1.5. Multi-GPUN.1.6. System AllocatorN.1.7. Hardware Coh…...
)
MySQL-其他函数(补充)
格式化函数FORMAT(x, n) 例:将数字x进行格式化,以四舍五入的方式保留n位小数,结果以字符串的形式返回mysql> select format(12.3456,3),format(2.2,4),format(9.333,0); --------------------------------------------------- | format(12…...
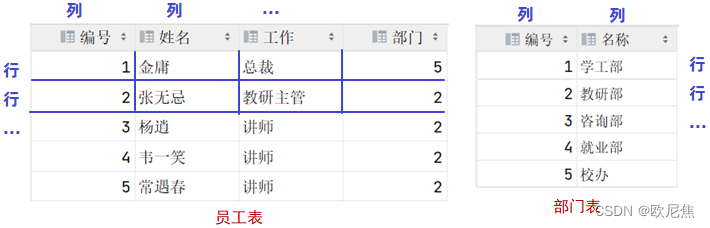
MySQL Study Notes Design in 2023
文章目录1 概述1.1 MySQL相关概述1.2 数据模型1.3 SQL分类2 数据库设计-DDL2.1 约束2.2 字段3 数据库操作-DML3.1 增加(insert)1 概述 1.1 MySQL相关概述 数据库:英文为 DataBase,简称DB,它是存储和管理数据的仓库。 数据库管理系统…...
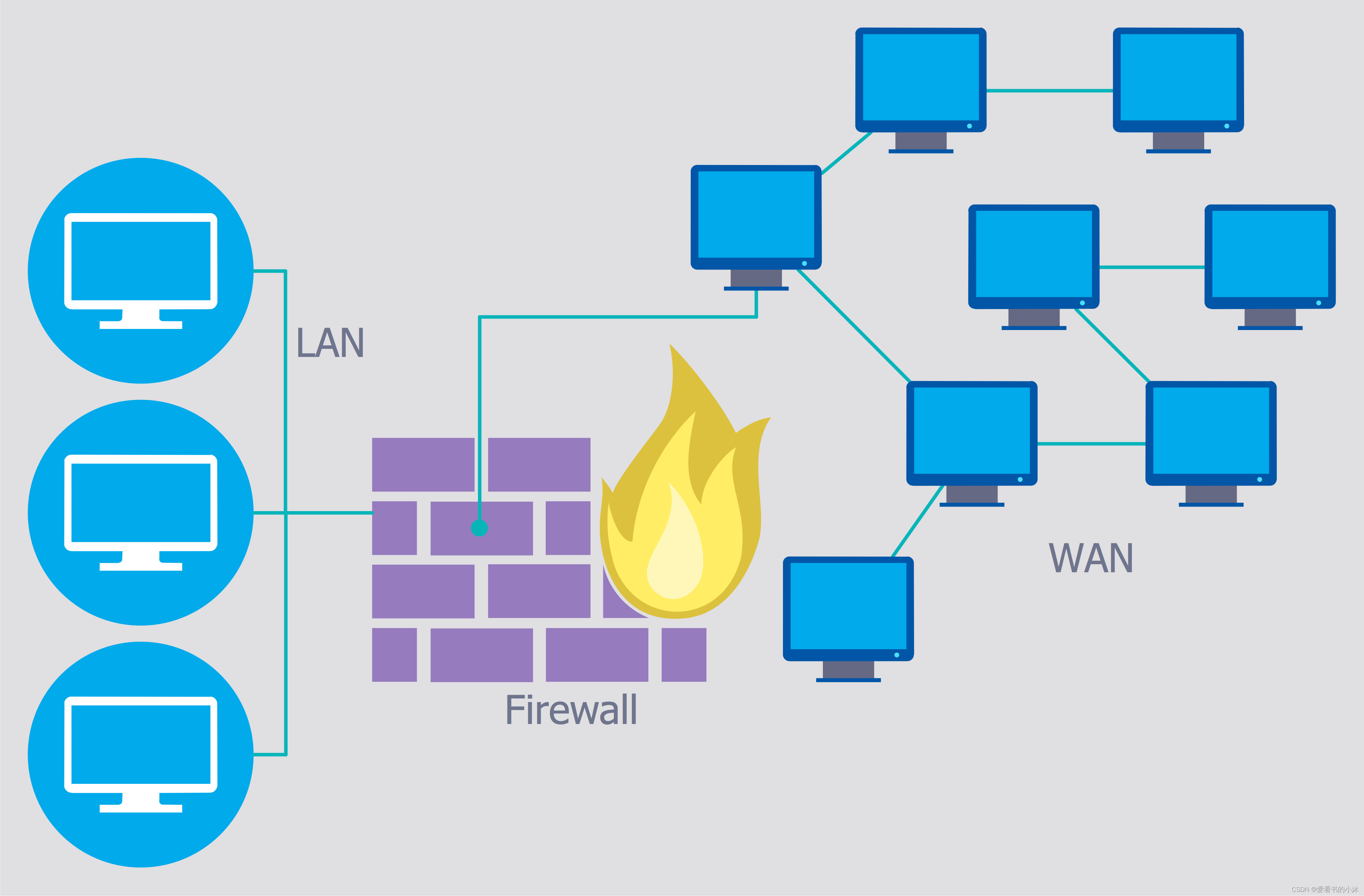
C++ 修改防火墙firewall设置(Windows)
文章目录1、简介1.1 防火墙概述1.2 入站,还是出站?1.3 防火墙规则优先级2、系统界面方式3、命令行方式3.1 防火墙基本状态设置3.2 入站出站规则设置3.3 其他设置3.4 telnet检测端口4、C方式4.1 注册表4.2 COM(Windows XP)4.3 COM&…...

Spring 入门教程详解
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...
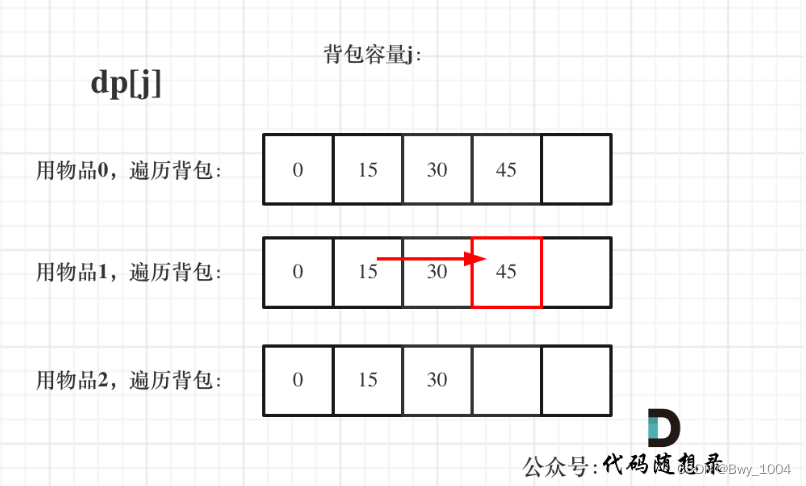
day43【代码随想录】动态规划之一和零、完全背包理论基础
文章目录前言一、一和零(力扣474)二、完全背包前言 1、一和零 2、完全背包理论基础 一、一和零(力扣474) 求装满这个背包最多有多少个物品 给你一个二进制字符串数组 strs 和两个整数 m 和 n 。 请你找出并返回 strs 的最大子集…...
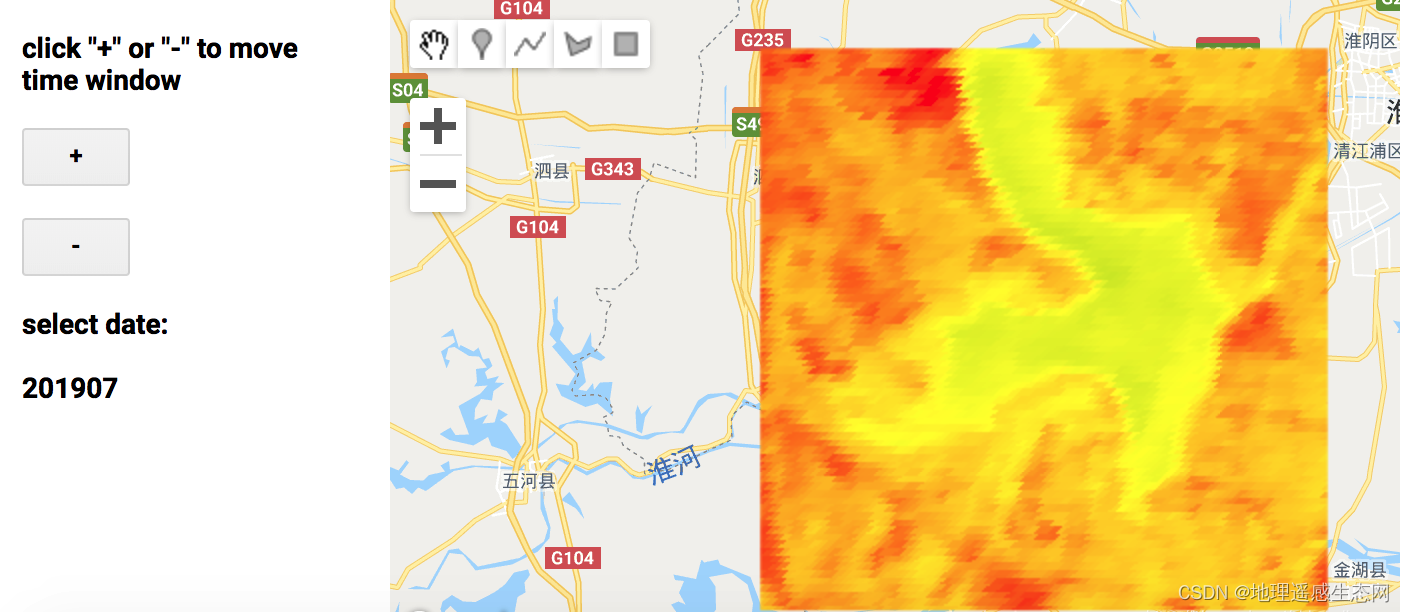
GEE学习笔记 七十八:干涸的洪泽湖
今天看了一篇报道直击60年一遇气象干旱:洪泽湖缩小近一半,鱼蟹受灾严重!_新华报业网(直击60年一遇气象干旱:洪泽湖缩小近一半,鱼蟹受灾严重!),既然玩GEE那就要玩出点花样…...

双指针【灵神基础精讲】
来源0x3f:https://space.bilibili.com/206214 文章目录同向双指针[209. 长度最小的子数组](https://leetcode.cn/problems/minimum-size-subarray-sum/)[713. 乘积小于 K 的子数组](https://leetcode.cn/problems/subarray-product-less-than-k/)[3. 无重复字符的最…...

tushare量化数据库模块怎么分析?
tushare量化数据其实包含的数据库有些是需要收费的,也有些会免费提供,不过tushare量化数据库整个库就很大很大,涉及的范围也广,挖掘这些数据还得从量化股票接口说起,就比如说在股票量化领域,tushare量化数据…...

模型转换 PyTorch转ONNX 入门
前言 本文主要介绍如何将PyTorch模型转换为ONNX模型,为后面的模型部署做准备。转换后的xxx.onnx模型,进行加载和测试。最后介绍使用Netron,可视化ONNX模型,看一下网络结构;查看使用了那些算子,以便开发部署…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...
