问卷数据分析流程
文章目录
- 一、数据合并
- 1. 读取数据
- 2. 数据预览
- 二、数据清洗
- 1. 检验ID是否重复,剔除ID重复项
- 2. 剔除填写时间小于xx分钟的值
- 3.处理 量表题 一直选一个选项的问题
- 三、数据清洗
- 1.1 将问卷单选题的选项code解码,还原成原来的选项
- 1.2 自动获取单选题旧的选项列表,进行替换成想要的选项名称
- 2.将多选题编码成0、1布尔值
- 四、数据分析
- 4.1 多选题 整体分析
- 4.2 快速对多个单选题同时分析
- 4.3 多选 交叉 单选题 分析
- 4.4 单选交叉单选
- 4.5 排序题分析
- 4.6 快速对多个多选题进行分析
一、数据合并
1. 读取数据
import pandas as pd
data = pd.read_excel('模块化床CMF调研_数据合并_202203.xlsx')
2. 数据预览
二、数据清洗
1. 检验ID是否重复,剔除ID重复项
检查是否有重复项,若无,返回0
print('ID重复的个数:',data.duplicated(subset=['ID'], keep='first').sum() )
如果有就删除
data = data.drop_duplicates(subset=['ID'], keep='first')
2. 剔除填写时间小于xx分钟的值
data['Time Finished'] = pd.to_datetime(data['Time Finished'])
data['Time Started'] = pd.to_datetime(data['Time Started'])data['Duration_time'] = data['Time Finished'] - data['Time Started']
# 观察什么样的填答时间是异常的
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as pltdef plot_numeric_features_distribution(feature_data,plt_title):from scipy.stats import normfrom scipy import statssns.distplot(feature_data, fit=norm)mu,sigma = norm.fit(feature_data)plt.legend(['Normal dist.($\mu=$ {:.2f} and$\sigma=${:.2f})'.format(mu,sigma)],loc='best')plt.ylabel('Frequency')plt.title(plt_title) fig = plt.figure()res = stats.probplot(feature_data, plot=plt)plt.show()
#调用函数
plot_numeric_features_distribution(data['时间2'],'none')筛选出 填写用时大于110s的样本
df = data[data['Duration_time'].dt.total_seconds()>110]
3.处理 量表题 一直选一个选项的问题
# 判断量表题是否 选同一个数
def judge(x):list9=['9、与伴侣同睡时,以下原因多大程度会影响您的睡眠?—作息时间不同','9、对床垫的软硬度要求不同','9、对方打鼾','9、对方翻身/上下床','9、对于睡眠温度要求不同']list17 = ['17、购买后,您对于【[q2]】各方面的满意度是?—床垫价格','17、床垫质量','17、床垫舒适度','17、床垫功能卖点','17、店铺促销优惠','17、品牌知名度','17、品牌口碑','17、售后服务','17、床垫外观',]list21=[ '21、未来,您会因为以下特性而购买左右分体床垫吗?—男女左右分区可选不同软硬度','21、更好的抗干扰性能','21、女方一侧,可因怀孕/产后需要更换床垫','21、男方一侧,带有辅助止鼾功能','21、左右拆分后方便搬运',]list22=['22、未来,您可能因为什么原因不考虑左右分体床垫—分体床垫中间区域可能会有缝隙感','22、文化风俗/情感方面会感到有隔阂','22、价格会比普通床垫贵','22、市场现有产品少,无法体验购买','22、跟伴侣睡眠质量好/暂无伴侣,没有需要','22、对质量感到担心',]list_sum = [list9,list17,list21,list22]mid_num = 0 # 过程存储,如果一个量表题全部选项一样就+1for i in list_sum:if len(set(x[i]))==1 and sum(x[i])/len(x[i]) != -3:mid_num+=1else:pass# 如果量表题有2题都是选择同一选项,则判为异常值if mid_num>=3:return Falseelse:return True三、数据清洗
1.1 将问卷单选题的选项code解码,还原成原来的选项
old_code_list = ['lower_i','lower_ii','middle_i','middle_ii','high_i','high_ii','high_iii','prefer_not_to_say']
real_option_list = ['<$2.5万','$2.5万-5万','$5万-7.5万','$7.5万-10万','$10万-12.5万','$12.5万-15万','>$15万','不愿透露']
df = df.reset_index(drop=True)
df['New_Income'] = df['Income'].replace(old_code_list,real_option_list)
1.2 自动获取单选题旧的选项列表,进行替换成想要的选项名称
# 获取原来单选题的选项有哪些
single_question = 'What kind of bed upholstered material do you like? (Please ignore color)'
old_code_list = list(df_multi_options[single_question].unique())
old_code_list
real_option_list = ['海军蓝','绿色','灰蓝色','米黄色','灰色','数字薰衣草','红色','黑色','棕褐色']
df_multi_options = df_multi_options.reset_index(drop=True)
df_multi_options[single_question] = df_multi_options[single_question].copy().replace(old_code_list,real_option_list)
df_multi_options[single_question].value_counts()
2.将多选题编码成0、1布尔值
未处理的多选题长这样
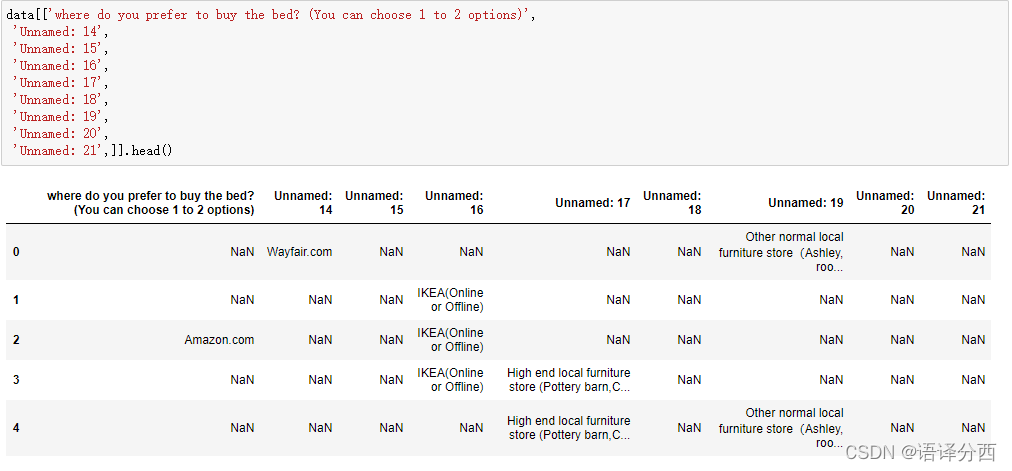
通过处理
# 1. 将要分析的多选题列表存入 “multi_options_list”
old_multi_options_list = ['where do you prefer to buy the bed? (You can choose 1 to 2 options)','Unnamed: 14','Unnamed: 15','Unnamed: 16','Unnamed: 17','Unnamed: 18','Unnamed: 19','Unnamed: 20','Unnamed: 21',]# 复制个备份
df_multi_options = data.copy()# 2. 获取多选题 选项的列表
multi_options_list = []
for i in old_multi_options_list:option_name = list(set(df_multi_options[i].dropna()))[0]multi_options_list.append(option_name)# 3. 将得到的选项列表和 旧的被编码的多选题列名,编成字典{'old name':'new name'}
name_dict = dict(zip(old_multi_options_list,multi_options_list))# 4.更替列表名称
df_multi_options = df_multi_options.rename(columns = name_dict)# 5.将空值填上 0
df_multi_options[multi_options_list] = df_multi_options[multi_options_list].fillna(0)# 6.将非空(也就是被选的)填上1def fill_one(x):if str(x) != '0':return 1else:return 0for i in multi_options_list:df_multi_options[i] = df_multi_options[i].apply(lambda x:fill_one(x))
得到
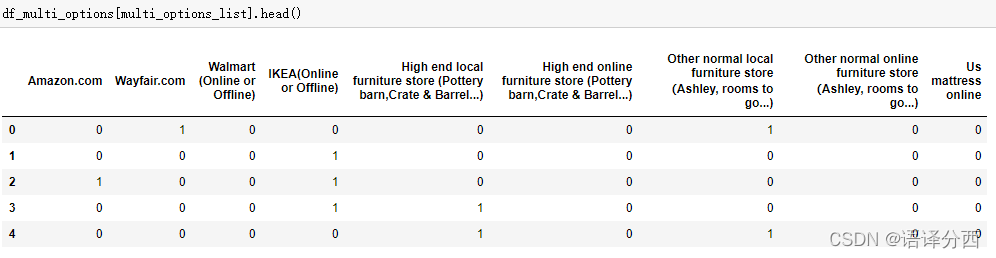
四、数据分析
4.1 多选题 整体分析
duoxuanti_option_list = [ '第36题-多选题-除了免费送货上门,您更偏好以下哪3种售后服务 \n[1]每年定期上门保养\n ','第36题-多选题-除了免费送货上门,您更偏好以下哪3种售后服务 \n[2]配送床垫时可处理旧床垫\n ','第36题-多选题-除了免费送货上门,您更偏好以下哪3种售后服务 \n[3]100%准时配送\n ','第36题-多选题-除了免费送货上门,您更偏好以下哪3种售后服务 \n[4]100天试睡\n ','第36题-多选题-除了免费送货上门,您更偏好以下哪3种售后服务 \n[5]可提供专业杀菌除螨仪\n ','第36题-多选题-除了免费送货上门,您更偏好以下哪3种售后服务 \n[6]上门清洗床垫污渍\n ','第36题-多选题-除了免费送货上门,您更偏好以下哪3种售后服务 \n[7]同城可免费再搬运一次\n ']def analyze_duoxuanti(data,duoxuanti_option_list):mid_df = data[duoxuanti_option_list].sum().rename_axis('选项').reset_index(name='计数')mid_df['选项'] = mid_df['选项'].apply(lambda x:re.findall(r"](.+?)\n",x))mid_df['选项'] = mid_df['选项'].apply(lambda x:x[0])fenmu = data[duoxuanti_option_list].dropna(how='all',axis=0).shape[0]mid_df['占比'] = mid_df['计数']/fenmureturn mid_df
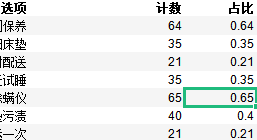
4.2 快速对多个单选题同时分析
1.筛选出单选题,组成列表
danxuanti_list = []
# 找出属性名中包含“单选题”字样的属性
for i in list2:if '单选' in i:danxuanti_list.append(i)
2.构建函数,对多个单选题数据进行分析
def analyze_many_danxuanti(data,danxuanti_list):df_list=[] # 创建个空列表,存储之后分析好的每个单选题的dataframe结果for i,danxuan in enumerate(danxuanti_list):# 计算每个单选题,统计频数,计数时要去掉空置,然后重命名列名middle_df1 = data[danxuan].value_counts(dropna=False).rename_axis(danxuan).reset_index(name='计数')middle_df2 = data[danxuan].value_counts(normalize=True,dropna=False).rename_axis(danxuan).reset_index(name='占比')merge_df = pd.merge(middle_df1,middle_df2,on=danxuan)exec("df_{} = merge_df".format(i))exec("df_list.append(df_{})".format(i)) with pd.ExcelWriter('单选统计分析结果.xlsx') as writer: for df in df_list:df_name = df.columns[0]df.to_excel(writer,sheet_name=df_name[:15],index=False)df_output= pd.concat(df_list,axis=1)return df_output
analyze_many_danxuanti(data,danxuanti_list)
4.3 多选 交叉 单选题 分析
single_option_list = ['<$2.5万','$2.5万-5万','$5万-7.5万','$7.5万-10万','$10万-12.5万','$12.5万-15万','>$15万']
single_option = 'New_Income'
multi_options_list
df_multi_options
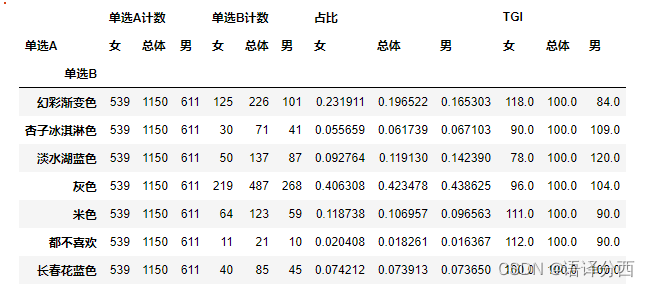
def multi_vs_single_option_analysis(df_multi_options,multi_options_list,single_option,single_option_list):"""df_multi_options是将多选题的答案从选项字符串编码成0、1后的处理结果dataframe,multi_options_list是多选题列名,例如[亚马逊、宜家、沃尔玛],single_option是单选题列名,例如:"年收入",single_option_list是单选题的选项列表,例如:[低收入、中收入、高收入]"""# 1. 交叉分析,需要知道其中一个属性下有哪些选项,通常是用户属性/用户标签,比如说8大策略人群标签#option_list_A = ['Z世代','潮流租客','精致型男','轻奢熟女','城乡小资','小镇百姓','品质中产','实惠中年'] 列表选项#option_A = '策略人群' 列表名for o in single_option_list: df_combine = df_multi_options[multi_options_list+[single_option]].copy()df_list = []for i,danxuan in enumerate(single_option_list):danxuan_df = df_combine[df_combine[single_option]==danxuan] # 提取 某 选项下的样本danxuan_num = danxuan_df.shape[0] # 该单选下样本数量单选 = []多选 = []单选计数 = []多选计数 = []占比 = []for m in multi_options_list:duoxuan_num = danxuan_df[m].sum() # 该单选下选择该多选的数量zhanbi = duoxuan_num/danxuan_num单选.append(danxuan)多选.append(m)单选计数.append(danxuan_num)多选计数.append(duoxuan_num)占比.append(zhanbi)df_middle=pd.DataFrame(zip(单选,多选,单选计数,多选计数,占比),columns=['单选','多选','单选计数','多选计数','占比'])df_middle = df_middle.sort_values(by=['占比'],ascending=False) # 排序exec("df_{} = df_middle".format(i))exec("df_list.append(df_{})".format(i)) df1 = pd.concat(df_list,axis=0)df1 = df1.reset_index(drop=True) #索引重置 单选2 = []多选2 = []单选计数2 = []多选计数2 = []占比2 = []TGI = []total_num = df_combine.shape[0]for m in multi_options_list:duoxuan_num2 = df_combine[m].sum() # 该人群选择该选项的数量zhanbi2 = duoxuan_num2/total_num单选2.append('总体')多选2.append(m)多选计数2.append(duoxuan_num2)单选计数2.append(total_num)占比2.append(zhanbi2)TGI.append(100)# 计算该问卷问题下总体样本的选择分布df_zongti=pd.DataFrame(zip(单选2,多选2,单选计数2,多选计数2,占比2,TGI),columns=['单选','多选','单选计数','多选计数','占比','TGI'])df_zongti = df_zongti.sort_values(by=['占比'],ascending=False)df_zongti = df_zongti.reset_index(drop=True)def calculate_tgi(x):zongti_zhanbi = df_zongti[df_zongti['多选']==x['多选']]['占比']tgi = round(x['占比']/(zongti_zhanbi),2)*100return tgi.values[0]df1['TGI']=df1.apply(lambda x:calculate_tgi(x),axis=1)output = pd.concat([df1,df_zongti])output = output.reset_index(drop=True)return output4.4 单选交叉单选
single_option_A = 'New_Income'
single_option_B = 'What is your budget for a upholstered bed(without mattress) in the master bedroom?'single_option_list_A = list(df_multi_options[single_option_A].unique())
#list(df_multi_options[single_option_A].unique())
single_option_list_B = list(df_multi_options[single_option_B].unique())df_multi_optionsdef single_vs_single_option_analysis(df_multi_options,single_option_A,single_option_list_A,single_option_B,single_option_list_B):# 1. 交叉分析,需要知道其中一个属性下有哪些选项,通常是用户属性/用户标签,比如说8大策略人群标签#single_option_list_A = ['Z世代','潮流租客','精致型男','轻奢熟女','城乡小资','小镇百姓','品质中产','实惠中年'] 列表选项#single_option_A = '策略人群' 列表名# 2.要将另一个单选题进行dummies化single_B_dummies_df = pd.get_dummies(df_multi_options[[single_option_B]],columns=[single_option_B]) # 3. 将dummies后的df 列表名去除 题目字符串,只保留选项字符串的列名old = single_B_dummies_df.columns.tolist()new = [x.replace(single_option_B+'_','') for x in old]name_dict = dict(zip(old,new))single_B_dummies_df= single_B_dummies_df.rename(columns =name_dict)
# print(single_B_dummies_df.columns.tolist())df_combine = pd.concat([single_B_dummies_df,df_multi_options[[single_option_A]]],axis=1)df_list = []for i,danxuan_a in enumerate(single_option_list_A):danxuan_a_df = df_combine[df_combine[single_option_A]==danxuan_a] # 提取单选a,某选项下的样本danxuan_a_num = danxuan_a_df.shape[0] # 该单选下样本数量单选A = []单选B = []单选A计数 = []单选B计数 = []占比 = []for m in single_option_list_B:danxuan_b_num = danxuan_a_df[m].sum() # 该单选下选择该多选的数量zhanbi = danxuan_b_num/danxuan_a_num单选A.append(danxuan_a)单选B.append(m)单选A计数.append(danxuan_a_num)单选B计数.append(danxuan_b_num)占比.append(zhanbi)df_middle=pd.DataFrame(zip(单选A,单选B,单选A计数,单选B计数,占比),columns=['单选A','单选B','单选A计数','单选B计数','占比'])df_middle = df_middle.sort_values(by=['占比'],ascending=False) # 排序exec("df_{} = df_middle".format(i))exec("df_list.append(df_{})".format(i)) df1 = pd.concat(df_list,axis=0)df1 = df1.reset_index(drop=True) #索引重置 单选A2 = []单选B2 = []单选B计数2 = []单选A计数2 = []占比2 = []TGI = []total_num = df_combine.shape[0]for m in single_option_list_B:danxuan_b_num2 = df_combine[m].sum() zhanbi2 = danxuan_b_num2/total_num单选A2.append('总体')单选B2.append(m)单选B计数2.append(danxuan_b_num2)单选A计数2.append(total_num)占比2.append(zhanbi2)TGI.append(100)# 计算该问卷问题下总体样本的选择分布df_zongti=pd.DataFrame(zip(单选A2,单选B2,单选A计数2,单选B计数2,占比2,TGI),columns=['单选A','单选B','单选A计数','单选B计数','占比','TGI'])df_zongti = df_zongti.sort_values(by=['占比'],ascending=False)df_zongti = df_zongti.reset_index(drop=True)def calculate_tgi(x):zongti_zhanbi = df_zongti[df_zongti['单选B']==x['单选B']]['占比']tgi = round(x['占比']/(zongti_zhanbi),2)*100return tgi.values[0]df1['TGI']=df1.apply(lambda x:calculate_tgi(x),axis=1)output = pd.concat([df1,df_zongti])output = output.reset_index(drop=True)return outputpd.pivot(outputdf,index='单选B',columns='单选A')
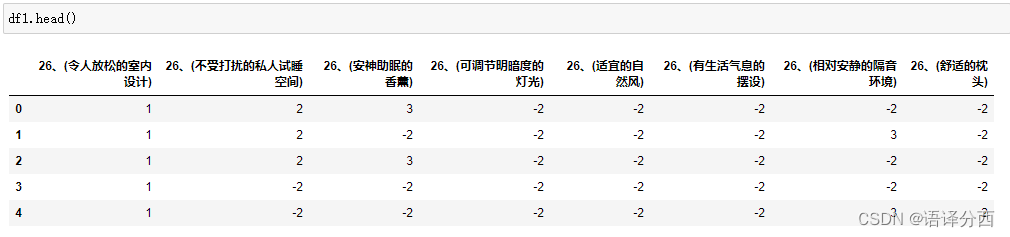
4.5 排序题分析
rank_question_list= [ '26、(令人放松的室内设计)','26、(不受打扰的私人试睡空间)','26、(安神助眠的香薰)','26、(可调节明暗度的灯光)','26、(适宜的自然风)','26、(有生活气息的摆设)','26、(相对安静的隔音环境)','26、(舒适的枕头)',]df1 = data[rank_question_list].copy()
def rank_question_process(x):# x 传入的是 排序题相关的dataframe rank_df = x.copy()option_list= rank_df.columns.tolist() # 获取排序题的选项列表rank_option_num = len(option_list) # 获取该排序题有几个选项paiming_list = [a+1 for a in range(rank_option_num)] # 选项的排名列表 [1.2.3.4.5.....]score_list = sorted(paiming_list,reverse=True) # 选项得分列表[8,7,6,5,...] ,排名越高,得分越高paiming_score_dict = dict(zip(paiming_list,score_list)) #假设排序题有8个选项→{1:8,2:7,3:6,4:5,5:4,6:3,7:2,8:1} # 有些平台排序题如果没有设置需要进行全部排序,有些就会跳过,问卷星跳过的值是 -2,需要进行处理paiming_score_dict[-2]=-2# 得到 排序,得分替换好的 dataframe数据for option in option_list:rank_df[option] = rank_df[option].apply(lambda x:paiming_score_dict[x])option_score_list = [] # 用于存储每个选项的排序得分for option in option_list:mid_list = []for n in rank_df[option].tolist():if n != -2: #如果值不等于-2(跳过),就需要添加进 中间列表中mid_list.append(n)# option_score= sum(mid_list)/len(mid_list) # 求平均得分,这里样本去除了跳过的样本option_score= sum(mid_list)/len(rank_df[option].tolist()) # 这里分母包含了跳过的样本option_score_list.append(option_score)output_df = pd.DataFrame({'选项':option_list,'排序得分':option_score_list})output_df = output_df.sort_values(by='排序得分',ascending=False) # 降序排序return output_df
rank_question_process(df1)
4.6 快速对多个多选题进行分析
整理提取,多选题
duoxuanti_list = []
# 找出属性名中包含“单选题”字样的属性
for i in option_list:if '多选' in i:duoxuanti_list.append(i)first3_str_list = list(set([d[:3] for d in duoxuanti_list])) # 提取每个多选题的头三个字符,题号# 处理多选题,一个多选题一个list,多个多选题list存在一个list里
duoxuanti_processed_list = []
for f in first3_str_list:mid_duoxuan_list=[]for d in duoxuanti_list:if f in d:mid_duoxuan_list.append(d)else:passduoxuanti_processed_list.append(mid_duoxuan_list)
相关文章:

问卷数据分析流程
文章目录一、数据合并1. 读取数据2. 数据预览二、数据清洗1. 检验ID是否重复,剔除ID重复项2. 剔除填写时间小于xx分钟的值3.处理 量表题 一直选一个选项的问题三、数据清洗1.1 将问卷单选题的选项code解码,还原成原来的选项1.2 自动获取单选题旧的选项列…...

【观察】Solidigm P44 Pro SSD评测:原厂品质+软硬兼施=性能怪兽
众所周知,目前SSD(固态硬盘)已取代HDD(机械硬盘)成为电脑中常见的存储设备,特别是在技术创新的持续推动下,如今SSD的速度和效率都在不断地提高,从SATA2 3GB发展到SATA3 6GBÿ…...
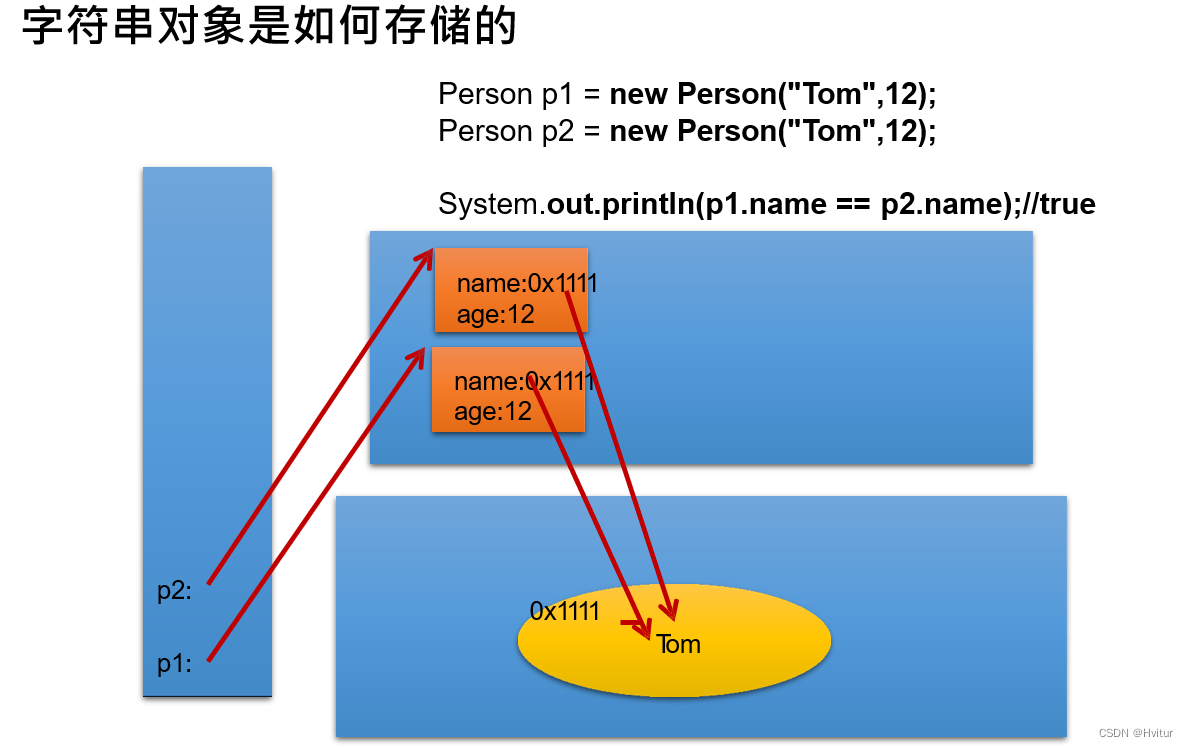
String对象的创建和比较
String类的概述 String类:代表字符串。 Java 程序中的所有字符串字面值(如 “abc” )都作 为此类的实例实现。 String是JDK中内置的一个类:java.lang.string 。 String表示字符串类型,属于引用数据类型,不…...
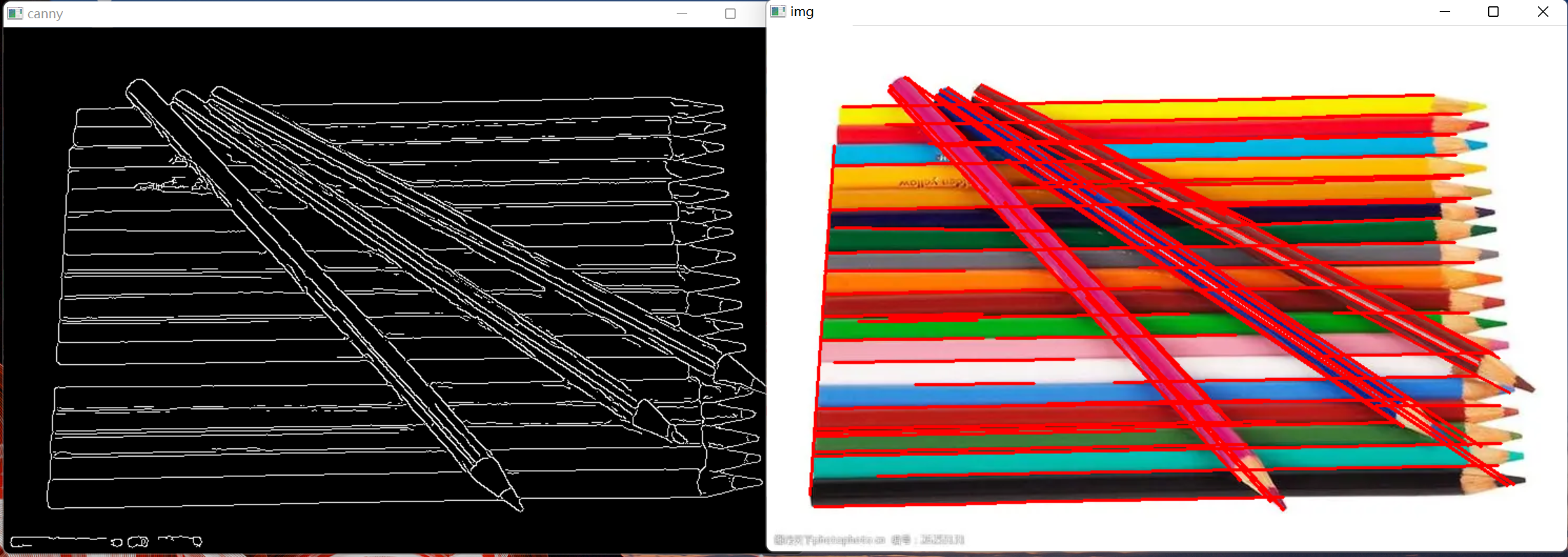
09 OpenCV图形检测
1 轮廓描边 cv2.findContours() 函数是OpenCV中用于寻找轮廓的函数之一。它可以用于在二值图像中查找并检测出所有的物体轮廓,以及计算出这些轮廓的各种属性,例如面积、周长、质心等。 cv2.findContours() 函数的语法如下: contours, hiera…...
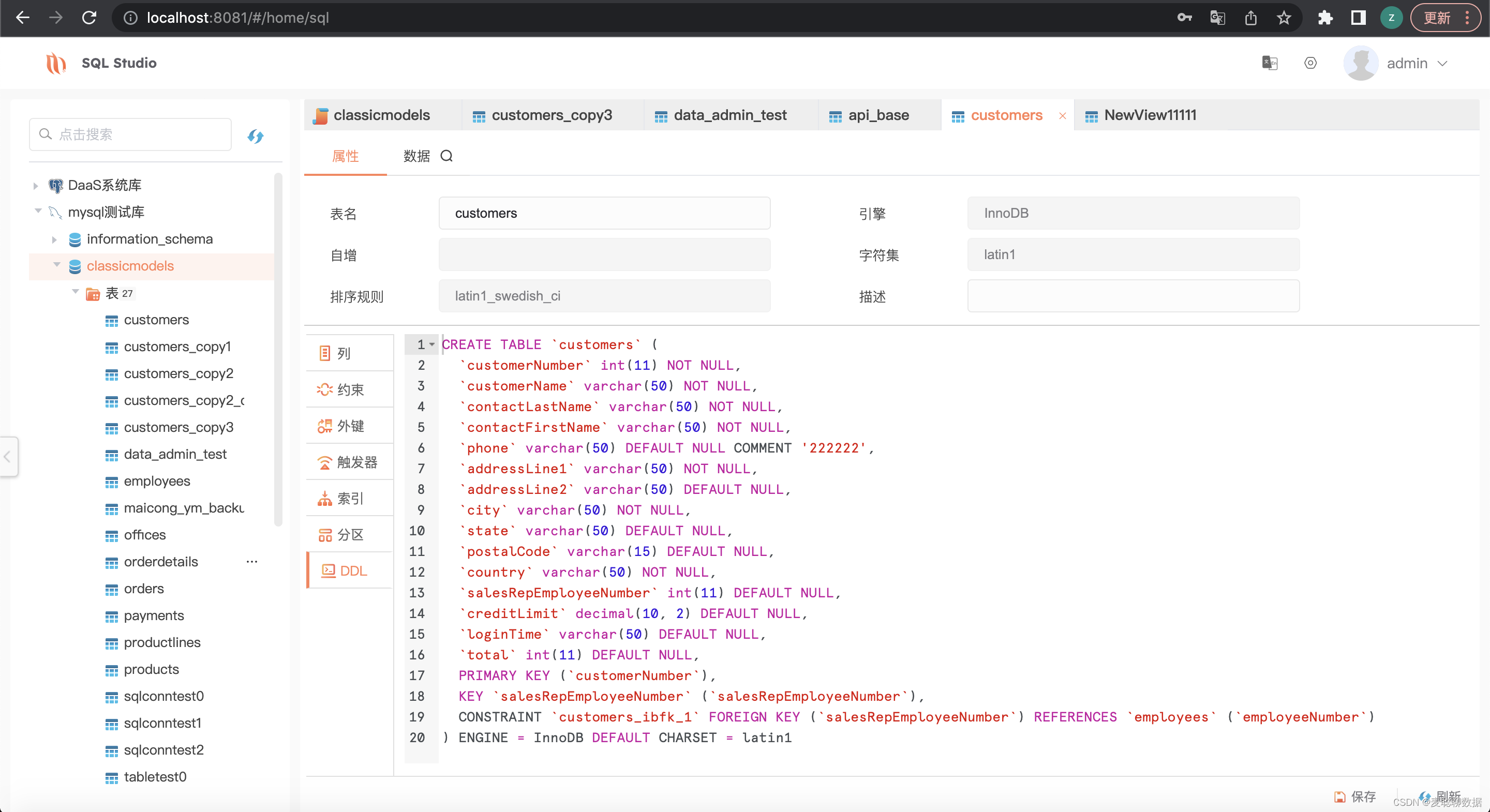
解密Teradata与中国市场“分手”背后的原因!国产数据库能填补空白吗?
2月15日,西方的情人节刚刚过去一天,国内IT行业就爆出一个大瓜。 继Adobe、甲骨文、Tableau、Salesforce之后,又一个IT巨头要撤离中国市场。 Teradata天睿公司官宣与中国市场“分手”,结束在中国的直接运营。目前,多家…...

Bernstein-Vazirani算法
B-V算法 (1) 问题描述 给定布尔函数f:{0,1}n→0,1f:{\left\{ {0,1} \right\}^n} \to{0,1}f:{0,1}n→0,1, 函数fff的值是由输入比特串xxx和确定的比特串sss做模2意义下的内积:f(x)x⋅s(mod2),f\left( x \right) x \cdot s\left( {\bmod 2} \right),f(x)x⋅s(mod2),…...

华为OD机试 - 相对开音节 | 备考思路,刷题要点,答疑 【新解法】
最近更新的博客 【新解法】华为OD机试 - 关联子串 | 备考思路,刷题要点,答疑,od Base 提供【新解法】华为OD机试 - 停车场最大距离 | 备考思路,刷题要点,答疑,od Base 提供【新解法】华为OD机试 - 任务调度 | 备考思路,刷题要点,答疑,od Base 提供【新解法】华为OD机试…...
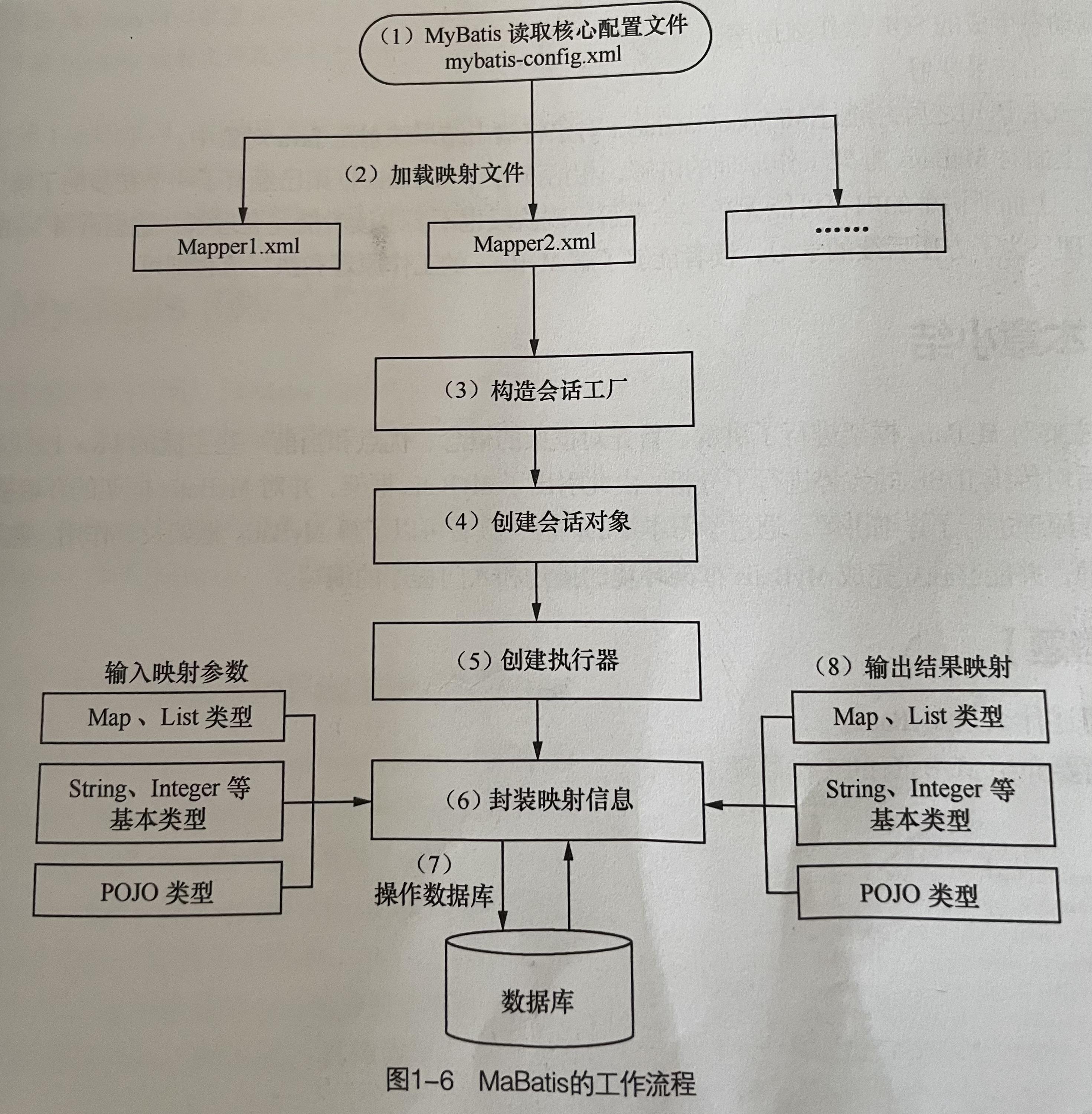
MyBatis
一、MyBatis环境搭建创建工程启动idea开发工具,选择工具栏中的“file”--“new”--“project”选项弹出“new project”对话框,编辑项目名称 选择maven项目,项目路径 单击 create 创建即可。引入相关依赖<dependencies><dependency&…...

良好的作息表
今天给大家带来“传说中”的“世界上最健康的作息时间表”(仅供参考),随时提醒自己吧,毕竟身体可是自己的哦。 7:30 起床:英国威斯敏斯特大学的研究人员发现,那些在早上5:22-7:21分起床的人,其血液中有一种能引起心脏病…...
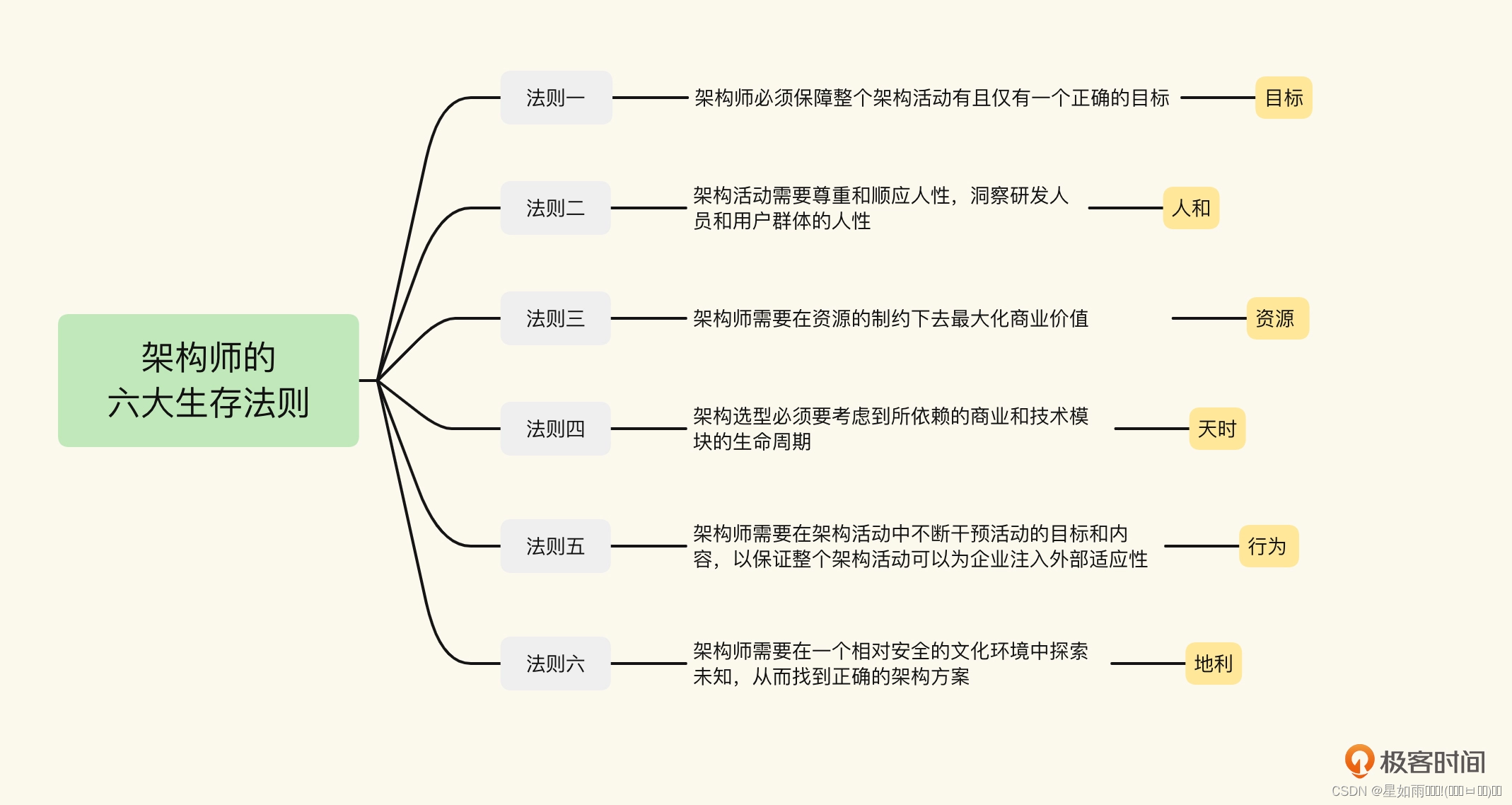
【郭东白架构课 模块一:生存法则】01|模块导学:是什么在影响架构活动的成败?
你好,我是郭东白。这节课是我们模块一的导入部分,我会先来介绍模块的主要内容,以及为什么我要讲生存法则这个话题。 一名软件架构师要为相对复杂的业务制定,并且引导实施一个结构化的软件方案。这个发现最终方案和推动实施的过程&…...

webshell免杀之函数与变量玩法
webshell免杀之函数与变量玩法 前言 前文列举了一些用符号免杀的例子,此篇文章就以函数和变量来尝试下免杀。 本文以PHP为例,用PHP中函数和变量及语法特性,在不隐藏函数关键字情况下进行免杀。 动态函数 PHP中支持一个功能叫 variable fu…...

【新解法】华为OD机试 - 去重求和 | 备考思路,刷题要点,答疑,od Base 提供
华为 OD 清单查看地址:blog.csdn.net/hihell/category_12199275.html 去重求和 | 备考思路,刷题要点,答疑,od Base 提供 给定一个数组,编写一个函数, 计算他的最大N个数和最小N个数的和, 需要对数组进行去重。 输入 第一行输入M,M表示数组大小 第二行输入M个数,表…...

MySQL 服务正在启动.MySQL 服务无法启动.服务没有报告任何错误。请键入 NET HELPMSG 3534 以获得更多的帮助。总结较全 (已解决)
输入以下命令启动mysql: net start mysql出现以下错误提示: MySQL 服务正在启动 .MySQL 服务无法启动。服务没有报告任何错误。请键入 NET HELPMSG 3534 以获得更多的帮助。 出现这个问题的话,一般有几个情况: 一、MySQL安装文…...

【数据结构与算法】数组2:双指针法 二分法(螺旋矩阵)
文章目录今日任务1.Leetcode977:有序数列的平方(1)题目(2)思路(3)暴力排序(4)双指针法2.Leetcode209:长度最小的子数组(1)题目&#x…...

librtmp优化
librtmp是一个RTMP的开源库,很多地方用它来做推流、拉流。它是RTMPDump开源软件里的一部分,librtmp的下载地址:RTMPDump,目前最新版是V2.3。本文重点介绍librtmp优化。 1、调整网络输出块大小。 RTMP_Connect0函数中LibRTMP是关…...

数据结构与算法(二):线性表
上一篇《数据结构与算法(一):概述》中介绍了数据结构的一些基本概念,并分别举例说明了算法的时间复杂度和空间复杂度的求解方法。这一篇主要介绍线性表。 一、基本概念 线性表是具有零个或多个数据元素的有限序列。线性表中数据…...
IOS安全区域适配
对于 iPhone 8 和以往的 iPhone,由于屏幕规规整整的矩形,安全区就是整块屏幕。但自从苹果手机 iphoneX 发布之后,前端人员在开发移动端Web页面时,得多注意一个对 IOS 所谓安全区域范围的适配。这其实说白了就是 iphoneX 之后的苹果…...
在Java 中 利用Milo通信库,实现OPCUA客户端,并生成证书
程序结构: 配置文件resources: opcua.properties 西门子PLC端口号为4840,kepserver为49320 #opcua服务端配置参数 #opcua.server.endpoint.urlopc.tcp://192.168.2.102:49320 opcua.server.endpoint.urlopc.tcp://192.168.2.11:4840 opcu…...

三分钟学会用Vim
Vim知识点 目录Vim知识点一:什么是vim二:vim常用的三种模式三:vim的基本操作一:什么是vim vim最小集 vim是一款多模式的编辑器—各种模式—每种模式的用法有差别—每种模式之间可以互相切换 但是我们最常用的就是3~5个模式 vi…...
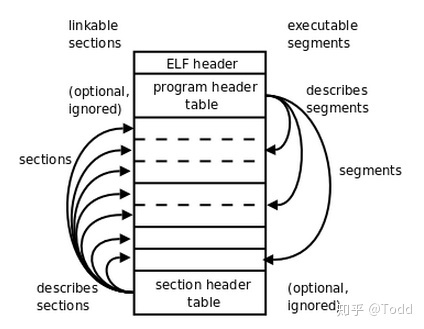
编译链接实战(8)认识elf文件格式
🎀 关于博主👇🏻👇🏻👇🏻 🥇 作者简介: 热衷于知识探索和分享的技术博主。 💂 csdn主页::【奇妙之二进制】 ✍️ 微信公众号:【Linux …...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...
