Easy Glide
题意:给出起点终点坐标,然后给出可以经过的几个点,未经过这几个点的时候以v1的速度前进,一旦经过这些点就可以在3秒内以v2的速度前进,3秒之后恢复v1,问从起点到终点所需的最短时间
思路:最短路模型没什么好说的,如果采用邻接表方式存图建边会比较麻烦,很遗憾我就是用的邻接表,注意从起点出发的点只能以v1的速度前进
ac代码:
#include<bits/stdc++.h>
#define endl '\n'
#define ll long long
#define INF 0x3f3f3f3f
#define pb push_back
#define int long long
#define Mirai ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
using namespace std;
typedef pair<int,int> pii;
const int N=1010;
pii _point[N];
int n;
double dist[N];
bool vis[N];
pii _start,_end;
vector<pair<int,double>> g[N];
double v1,v2;
double getdist(int sx,int sy,int tx,int ty)
{return sqrt((sx-tx)*(sx-tx)+(sy-ty)*(sy-ty));
}
double gettime(pii a,pii b,bool isv2)//isv2代表是否加速
{double len=getdist(a.first,a.second,b.first,b.second);double time;if(isv2){time=len/v2;if(time>3)time=3+(time-3)*v2/v1;}else time=len/v1;return time;
}
void dij()
{priority_queue<pair<double,int>,vector<pair<double,int>>,greater<pair<double,int>>> q;dist[n]=0;q.push({dist[n],n});while(q.size()){int u=q.top().second;q.pop();if(vis[u])continue;vis[u]=true;for(auto [v,w]:g[u]){if(dist[v]>dist[u]+w){dist[v]=dist[u]+w;q.push({dist[v],v});}}}
}
void solve()
{cin>>n;for(int i=0;i<=n+1;i++)dist[i]=1e9;for(int i=0;i<n;i++)cin>>_point[i].first>>_point[i].second;//将0加速点到n-1加速点的坐标存下来cin>>_start.first>>_start.second>>_end.first>>_end.second;//起点和终点的坐标cin>>v1>>v2;//假设起点为n,终点为n+1for(int i=0;i<n;i++){for(int j=0;j<n;j++)//对于每个加速点都向其他加速点以连一条边{g[i].pb({j,gettime(_point[i],_point[j],true)});}g[i].pb({n+1,gettime(_point[i],_end,true)});//再从每个点向终点连一条边}for(int i=0;i<n;i++)//从起点处发的边都是未加速的{g[n].pb({i,gettime(_start,_point[i],false)});//从起点向每个加速点连一条边}g[n].pb({n+1,gettime(_start,_end,false)});//从起点到终点连一条边dij();printf("%.12lf\n",dist[n+1]);
}
signed main()
{Mirai;int T=1;// cin>>T;while(T--){solve();}
}相关文章:

Easy Glide
题意:给出起点终点坐标,然后给出可以经过的几个点,未经过这几个点的时候以v1的速度前进,一旦经过这些点就可以在3秒内以v2的速度前进,3秒之后恢复v1,问从起点到终点所需的最短时间 思路:最短路…...
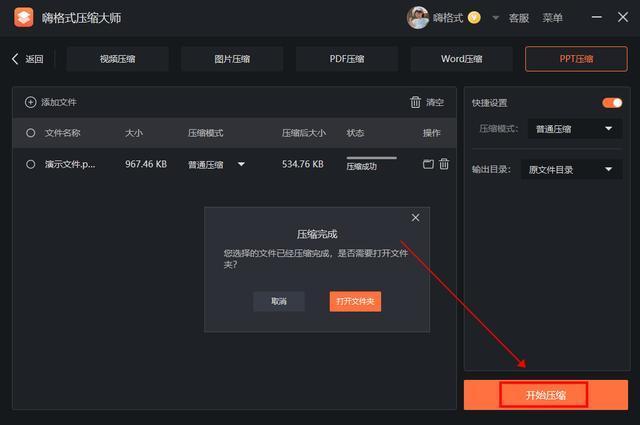
ppt怎么压缩到10m以内?分享好用的压缩方法
PPT是一种常见的演示文稿格式,有时候文件过大,我们会遇到无法发送、上传的现象,这时候简单的解决方法就是压缩其大小,那怎么才能将PPT压缩到10M以内呢? PPT文件大小受到影响的主要因素就是以下几点: 1、图…...

VBA技术资料MF35:VBA_在Excel中过滤数据
【分享成果,随喜正能量】好马好在腿,好人好在嘴。不会烧香得罪神,不会讲话得罪人。慢慢的你就会发现,一颗好心,永远比不上一张好嘴。。 我给VBA的定义:VBA是个人小型自动化处理的有效工具。利用好了&#…...
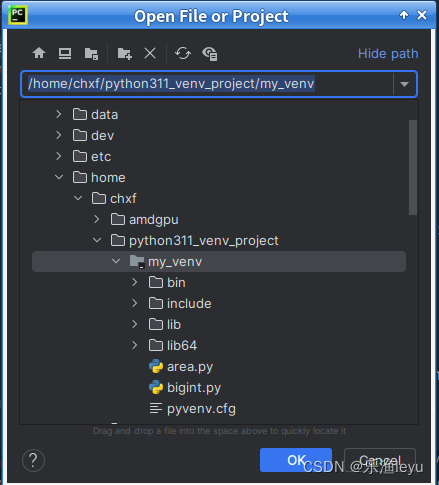
Debian12中为python3配置虚拟环境及在Pycharm中使用虚拟环境
在Debian 12中,python默认为python 3.11。 基于应用,现需设置虚拟环境。 1.安装venv模块 从python3.3开始,配置python虚拟环境,可用venv模块,更加方便了。 执行命令: #apt install python3.11-venv 2.…...

android app控制ros机器人一
android开发app,进而通过控制ros机器人,记录开发过程 查阅资料: rosjava使用较多,已经开发好的app也有开源的案例 rosjava GitHub https://github.com/ros-autom/RobotCA https://github.com/ROS-Mobile/ROS-Mobile-Android…...
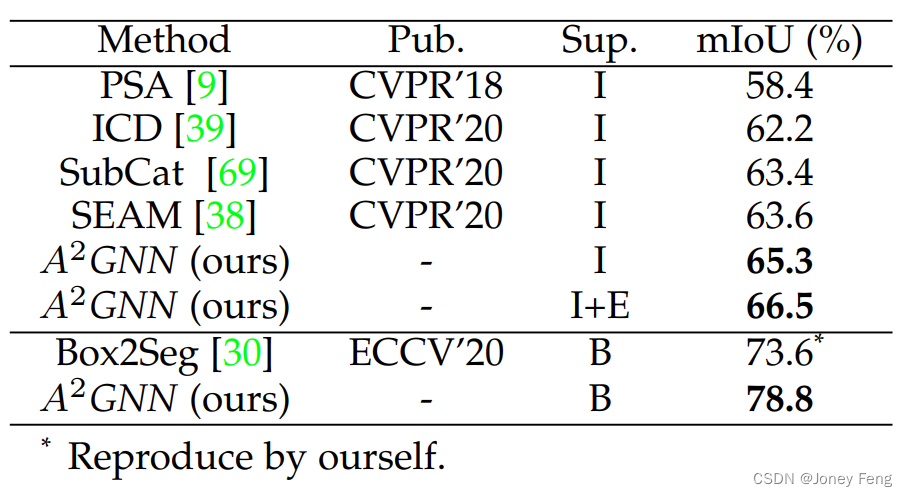
二十章:基于弱监督语义分割的亲和注意力图神经网络
0.摘要 弱监督语义分割因其较低的人工标注成本而受到广泛关注。本文旨在解决基于边界框标注的语义分割问题,即使用边界框注释作为监督来训练准确的语义分割模型。为此,我们提出了亲和力注意力图神经网络(A2GNN)。按照先前的做法&a…...

webpack5 学习之路
1.视频 01-课程介绍_哔哩哔哩_bilibili 2.配套资料 依赖环境 | 尚硅谷 Web 前端之 Webpack5 教程 3.webpack 官方文档 入口起点(entry points) | webpack 中文文档 4.vue cli 官方文档 介绍 | Vue CLI 挖矿:Coding Tree...

VSCode C++ 调试方法
VSCode 调试 C 主要就是 .vscode 中的 launch.json 和 tasks.json 的配置。 launch.json 可以通过 vscode 界面 ——》左侧调试功能按钮——》创建 launch.json ——》C(GDB/LLDB)生成。 其中 launch.json 默认配置如下,主要配置项说明&…...

Java设计模式-命令模式
命令模式 1.命令模式含义 命令模式,将一个请求封装为一个对象,从而使你可用不同的请求对客户进行参数化。对请求排队或记录请求日志,以及支持可撤销的操作。 命令模式乍一看,有点懵懵的。即使这个定义看完,也是不明…...

Linux编译宏BUILD_BUG_ON_ZERO
本系列文章主要写我在阅读Linux内核过程中,关注的比较难以理解但又设计巧妙的代码片段(不关注OS的各个模块的设计思想,此部分我准备写在“深入理解Linux Kernel”系列文章中),一来通过内核代码复习一下C语言及汇编语言…...

从Arweave开始:4EVERLAND存储签入挑战开始
嗨,4evers, 今天,我们热烈欢迎您参加 Galxe 上的 4EVERLAND “Arweave 入门”活动。这是一项长期的重头活动,所有参与的用户都有机会获得相应的奖励。 Arweave 是一种革命性的去中心化存储协议,为寻求安全可靠的有价…...
数据结构—链表
链表 前言链表链表的概念及结构链表的分类 无头单向非循环链表的相关实现带头双向循环链表的相关实现顺序表和链表(带头双向循环链表)的区别 前言 顺序表是存在一些固有的缺陷的: 中间/头部的插入删除,时间复杂度为O(N)…...
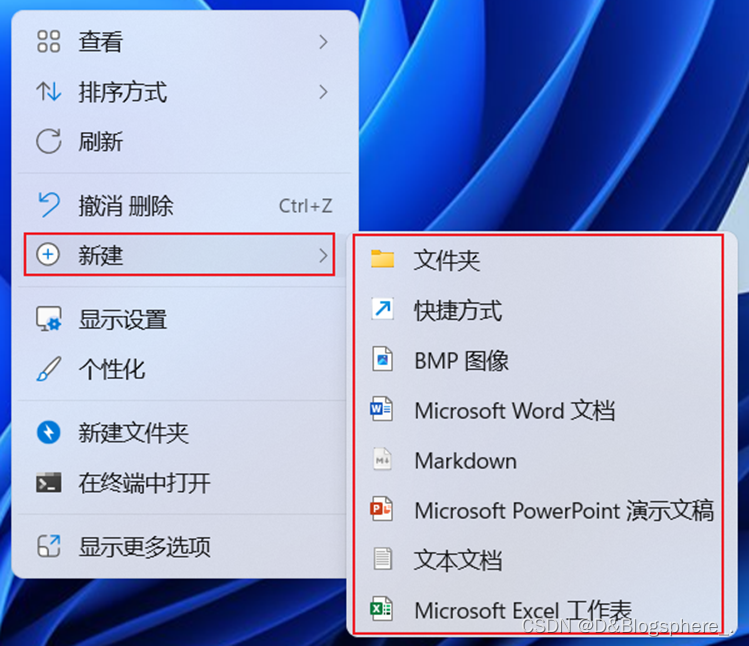
windows 10/11 修改右键新建菜单
问题:修改右键新建菜单内容 解决方法:使用软件ShellNew Settings 1.打开软件 2.根据需要取消勾选项 3.最终效果...

6.修饰符
文章目录 6.1 在一个静态方法内调用一个非静态成员为什么是非法的?6.2 静态方法和实例方法有何不同 6.1 在一个静态方法内调用一个非静态成员为什么是非法的? 由于静态方法可以不通过对象进行调用,因此在静态方法里,不能调用其他非静态变量࿰…...

【leetcode难题】2569. 更新数组后处理求和查询【线段树实现01翻转和区间求和模版】
题目截图 题目分析 关键就是记录每次操作2时,nums1中的1的个数这就需要实现线段树进行区间反转以及区间求和 ac code class Solution:def handleQuery(self, nums1: List[int], nums2: List[int], queries: List[List[int]]) -> List[int]:n len(nums1)m le…...
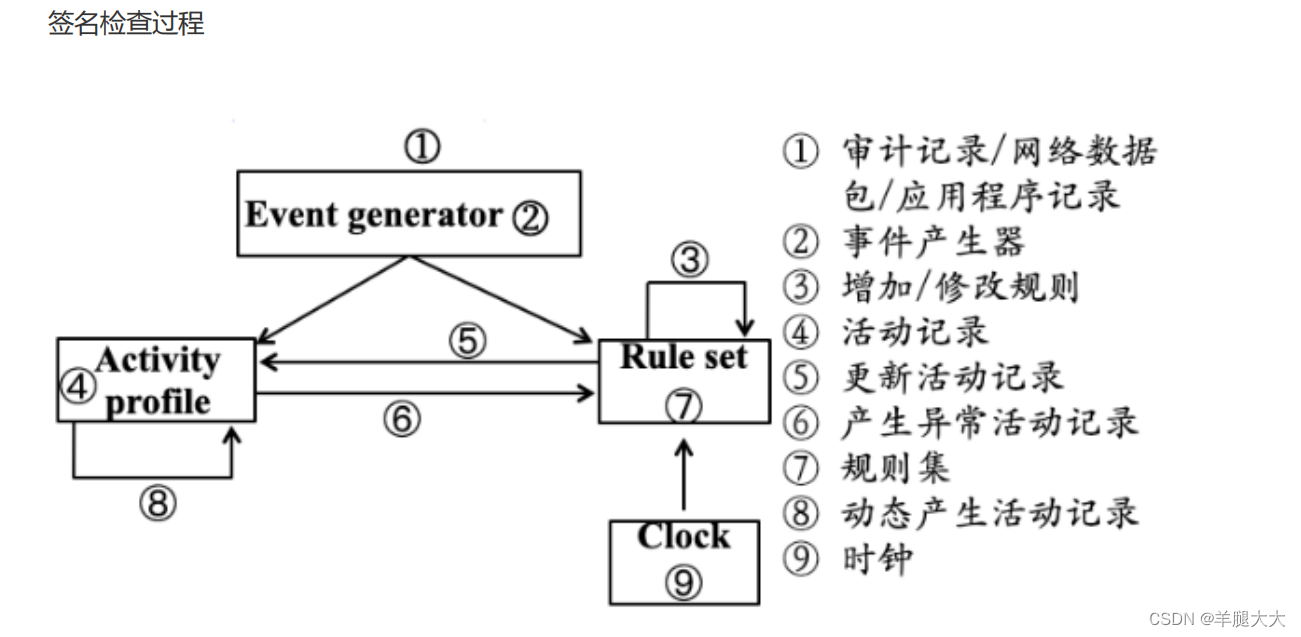
练习时长两年半的入侵检测
计算机安全的三大中心目标是:保密性 (Conf idential ity) 、完整性 (Integrity) 、可用性 (Availability) 。 身份认证与识别、访问控制机制、加密技术、防火墙技术等技术共同特征就是集中在系统的自身加固和防护上,属于静态的安全防御技术,…...

【弹力设计篇】聊聊隔离设计
为什么需要隔离设计 隔离其实就是Bulkheads,隔板。在生活中隔板的应用主要在船舱中进行设计,目的是为了避免因一处漏水导致整个船都沉下去。可以将故障减少在一定的范围内,而不是整个船体。 从架构演变来说的话,大多数系统都是从…...

MFC 透明窗体
如何制作透明窗体 ????? 使用SetLayeredWindowAttributes可以方便的制作透明窗体,此函数在w2k以上才支持,而且如果希望直接使用的话,可能需要下载最新的SDK。不过此函数在w2k的user32.dll里有实…...

C++笔记之vector的resize()和clear()用法
C笔记之vector的resize()和clear()用法 code review! 文章目录 C笔记之vector的resize()和clear()用法1.resize()2.clear() 1.resize() 运行 2.clear() 运行...

Vue2基础九、路由
零、文章目录 Vue2基础九、路由 1、单页应用 (1)单页应用是什么 单页面应用(SPA:Single Page Application): 所有功能在 一个html页面 上实现具体示例: 网易云音乐 https://music.163.com/ (2)单页面应用VS多页面…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...
