25.10 matlab里面的10中优化方法介绍—— 函数fmincon(matlab程序)
1.简述
关于非线性规划
非线性规划问题是指目标函数或者约束条件中包含非线性函数的规划问题。
前面我们学到的线性规划更多的是理想状况或者说只有在习题中,为了便于我们理解,引导我们进入规划模型的一种情况。相比之下,非线性规划会更加贴近实际的生活。那这节我们先通过一个类似于线性规划中linprog()函数的fmincon()来体会一下这类问题的解决过程。
一、fmincon()的基本形式
基本形式如下:x = fmincon(‘fun’,x0,A,b,Aeq,beq,lb,ub,‘nonlcon’,options) ;
(1)‘fun’为目标函数,注意需要单引号,或者@,或者直接在定义时写成匿名函数即可,后面的nonlcon为非线性约束(包括等式和不等式),形式要求同fun;
(2)x0表示决策变量的初始值,可以随机取一组符合约束条件的数据值,一般来讲没什么影响;
(3)A,b,Aeq,beq分别表示线性的不等式约束和等式约束,Ax<=b,Aeqx=beq;lb,ub同之前的linprog()函数,表示上下界的向量;
(4)使用 options 所指定的优化选项执行最小化。使用 optimoptions 可设置这些选项。如果没有非线性不等式或等式约束,请设置 nonlcon = []。
基本要求就是以上这些,下面我们以几个例子来具体实现一下。
2.代码
例子1
%% 用函数fmincon求约束最优化问题
clear all
f=inline('exp(x(1))*(4*x(1)^2+2*x(2)^2+4*x(1)*x(2)+2*x(2)+1)','x');
x0=[-1 1];
[x,fval]=fmincon(f,x0,[],[],[],[],[],[],'fcon1212')
例子2
%% 用fmincon解线性约束的最优化
clear all
f=inline('-x(1)*x(2)*x(3)','x');
A=[-1,-2,-2;1,2,2]; %A*x<=b
b=[0;72];
x0=[10;10;10];
[x,fval]=fmincon(f,x0,A,b)
3.运行结果


相关文章:

25.10 matlab里面的10中优化方法介绍—— 函数fmincon(matlab程序)
1.简述 关于非线性规划 非线性规划问题是指目标函数或者约束条件中包含非线性函数的规划问题。 前面我们学到的线性规划更多的是理想状况或者说只有在习题中,为了便于我们理解,引导我们进入规划模型的一种情况。相比之下,非线性规划会更加贴近…...
赛效:如何将PDF文件免费转换成Word文档
1:在网页上打开wdashi,默认进入PDF转Word页面,点击中间的上传文件图标。 2:将PDF文件添加上去之后,点击右下角的“开始转换”。 3:稍等片刻转换成功后,点击绿色的“立即下载”按钮,将…...

java 8 的Stream API
Java 8中引入了Stream API,它是一种处理集合数据的新方式,可以用来处理集合中的元素。Stream API通过提供一组函数式接口和方法,可以使集合的处理更加简洁、高效和易读。 Stream API的主要特点如下: 延迟执行:Stream …...

TypeChat,用TypeScript快速接入AI大语言模型
TypeChat是C# 和 TypeScript 之父 Anders Hejlsberg全新的开源项目。使用AI在自然语言和应用程序和API之间建立桥梁,并且使用TypeScript。 现在出现了很多大型语言模型,但是如何将这些模型最好地集成到现有的应用程序中,如何使用人工智能来接…...

Dcoker compose单机容器集群编排管理
目录 一、概述 二、compose 部署 lnmp 1.Docker Compose 环境安装 2.YAML 文件格式及编写注意事项 3.Docker Compose配置常用字段 4.Docker Compose 常用命令 5. 配置lnmp集群依赖文件 6.修改docker-compose.yml文件 7.根据yml文件创建lnmp容器 一、概述 Docker compos…...
)
P5635 【CSGRound1】天下第一(记忆化搜索)
用short类型二维数组防止MLE。这里用的记忆化搜索,如果f[x][y]已经有值了,直接返回这个值。判断error的方法:如果下一次又访问到它,说明出现了循环,这样是永远%不到0的,所以,第一次访问一次f[x]…...

如何维护你的电脑:提升性能和延长使用寿命
如何维护你的电脑:提升性能和延长使用寿命 😇博主简介:我是一名正在攻读研究生学位的人工智能专业学生,我可以为计算机、人工智能相关本科生和研究生提供排忧解惑的服务。如果您有任何问题或困惑,欢迎随时来交流哦&…...
Docker续集+Docker Compose
目录 Containerd与docker的关系 runCrunC与Containerd的关联 OCI协议Dockerfile多阶段构建(解决:如何让一个镜像变得更小 )多阶段构建Images瘦身实践.dockerignore Docker Compose快速开始Quick StartCompose 命令常用命令命令说明 Compose 模…...
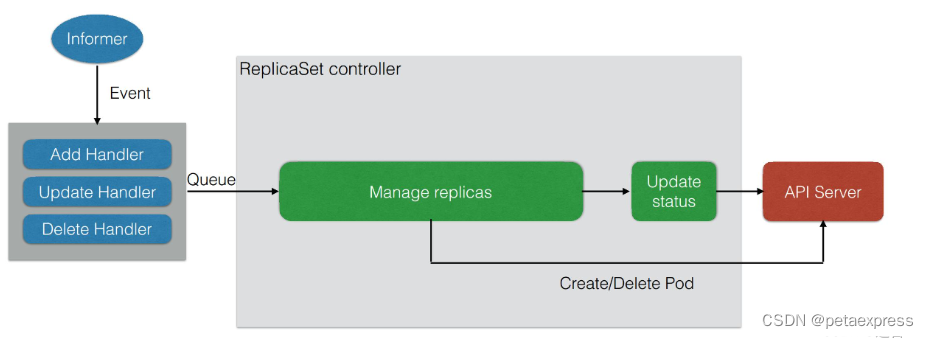
k8s deployment(k8s经典版)|PetaExpress
Deployment是什么? Deployment是指在软件开发中将应用程序或系统部署到目标环境中的过程。它包括将代码编译、配置、打包并安装到目标服务器或设备上的步骤。k8s deployment是(k8s经典版)中用来管理发布的控制器,在开发的过程中使…...

uni-app如何生成正式的APK
第一步: 进入dcloud官网https://dcloud.io/,点击开发者后台进入登录注册页面 第二步:登录之后跳到项目列表,选择自己想要打包的项目 点击进去如果没有生成证书,点击生成证书,如果显示证书已生成就不用管了…...
低代码开发平台源码:可视化敏捷开发工具,拖拽式自定义表单界面
低代码开发平台源码 低代码管理系统源码 无需代码或通过少量代码就可以快速生成应用程序的开发平台。 本套低代码管理后台可以支持多种企业应用场景,包括但不限于CRM、ERP、OA、BI、IoT、大数据等。无论是传统企业还是新兴企业,都可以使用管理后台快速构…...
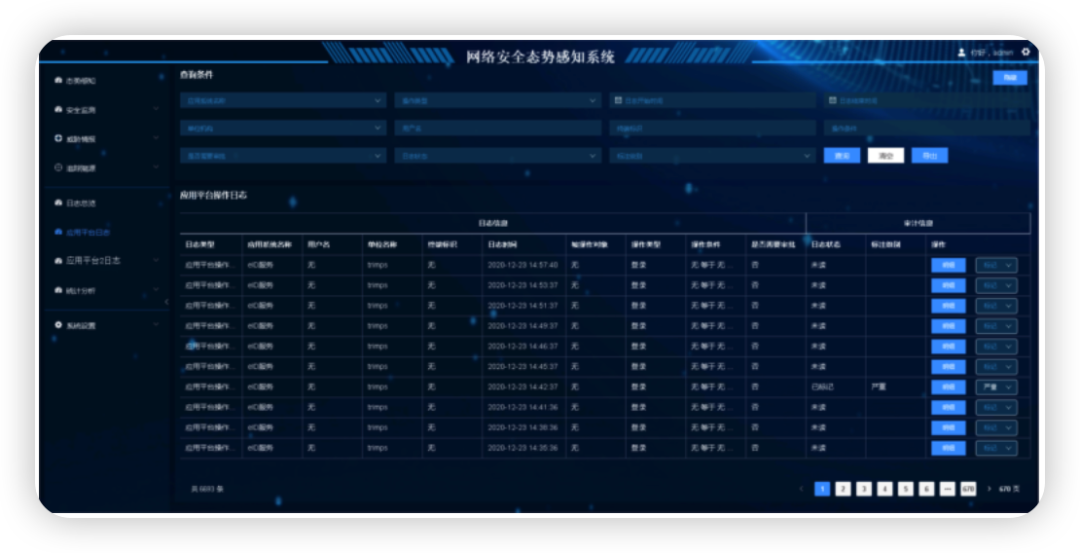
利用读时建模等数据分析能力,实现网络安全态势感知的落地
摘要:本文提出一种基于鸿鹄数据平台的网络安全态势感知系统,系统借助鸿鹄数据平台读时建模、时序处理、数据搜索等高效灵活的超大数据存储和分析处理能力,支持海量大数据存储、分类、统计到数据分析、关联、预测、判断的网络安全态势感知能力…...
六、代理模式
文章目录 一、代理模式1、代理模式的好处和缺点1.1 代理模式理解加深 一、代理模式 为什么要学习代理模式? 代理模式是Spring AOP 以及 Spring MVC 的底层!!并且还是 JAVA 的23种设计模式之一!! 代理模式的分类&#…...

Easy Glide
题意:给出起点终点坐标,然后给出可以经过的几个点,未经过这几个点的时候以v1的速度前进,一旦经过这些点就可以在3秒内以v2的速度前进,3秒之后恢复v1,问从起点到终点所需的最短时间 思路:最短路…...
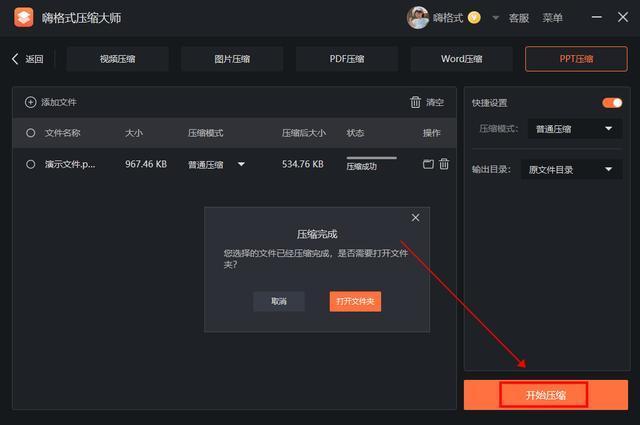
ppt怎么压缩到10m以内?分享好用的压缩方法
PPT是一种常见的演示文稿格式,有时候文件过大,我们会遇到无法发送、上传的现象,这时候简单的解决方法就是压缩其大小,那怎么才能将PPT压缩到10M以内呢? PPT文件大小受到影响的主要因素就是以下几点: 1、图…...

VBA技术资料MF35:VBA_在Excel中过滤数据
【分享成果,随喜正能量】好马好在腿,好人好在嘴。不会烧香得罪神,不会讲话得罪人。慢慢的你就会发现,一颗好心,永远比不上一张好嘴。。 我给VBA的定义:VBA是个人小型自动化处理的有效工具。利用好了&#…...
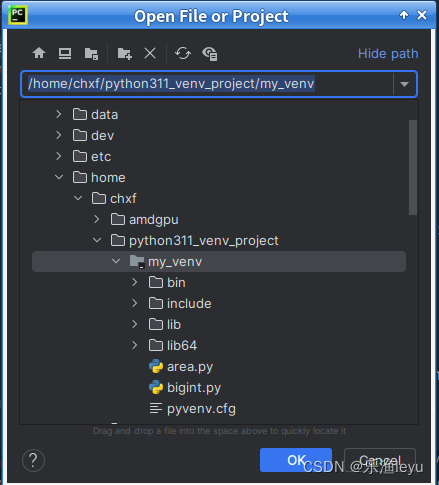
Debian12中为python3配置虚拟环境及在Pycharm中使用虚拟环境
在Debian 12中,python默认为python 3.11。 基于应用,现需设置虚拟环境。 1.安装venv模块 从python3.3开始,配置python虚拟环境,可用venv模块,更加方便了。 执行命令: #apt install python3.11-venv 2.…...

android app控制ros机器人一
android开发app,进而通过控制ros机器人,记录开发过程 查阅资料: rosjava使用较多,已经开发好的app也有开源的案例 rosjava GitHub https://github.com/ros-autom/RobotCA https://github.com/ROS-Mobile/ROS-Mobile-Android…...
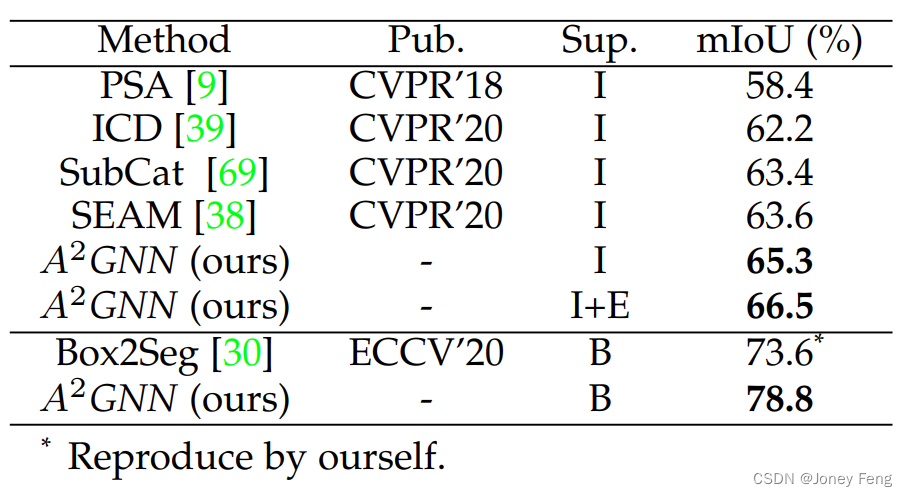
二十章:基于弱监督语义分割的亲和注意力图神经网络
0.摘要 弱监督语义分割因其较低的人工标注成本而受到广泛关注。本文旨在解决基于边界框标注的语义分割问题,即使用边界框注释作为监督来训练准确的语义分割模型。为此,我们提出了亲和力注意力图神经网络(A2GNN)。按照先前的做法&a…...

webpack5 学习之路
1.视频 01-课程介绍_哔哩哔哩_bilibili 2.配套资料 依赖环境 | 尚硅谷 Web 前端之 Webpack5 教程 3.webpack 官方文档 入口起点(entry points) | webpack 中文文档 4.vue cli 官方文档 介绍 | Vue CLI 挖矿:Coding Tree...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...

抽象类和接口(全)
一、抽象类 1.概念:如果⼀个类中没有包含⾜够的信息来描绘⼀个具体的对象,这样的类就是抽象类。 像是没有实际⼯作的⽅法,我们可以把它设计成⼀个抽象⽅法,包含抽象⽅法的类我们称为抽象类。 2.语法 在Java中,⼀个类如果被 abs…...

Vue 模板语句的数据来源
🧩 Vue 模板语句的数据来源:全方位解析 Vue 模板(<template> 部分)中的表达式、指令绑定(如 v-bind, v-on)和插值({{ }})都在一个特定的作用域内求值。这个作用域由当前 组件…...

WEB3全栈开发——面试专业技能点P7前端与链上集成
一、Next.js技术栈 ✅ 概念介绍 Next.js 是一个基于 React 的 服务端渲染(SSR)与静态网站生成(SSG) 框架,由 Vercel 开发。它简化了构建生产级 React 应用的过程,并内置了很多特性: ✅ 文件系…...

WEB3全栈开发——面试专业技能点P4数据库
一、mysql2 原生驱动及其连接机制 概念介绍 mysql2 是 Node.js 环境中广泛使用的 MySQL 客户端库,基于 mysql 库改进而来,具有更好的性能、Promise 支持、流式查询、二进制数据处理能力等。 主要特点: 支持 Promise / async-await…...

鸿蒙Navigation路由导航-基本使用介绍
1. Navigation介绍 Navigation组件是路由导航的根视图容器,一般作为Page页面的根容器使用,其内部默认包含了标题栏、内容区和工具栏,其中内容区默认首页显示导航内容(Navigation的子组件)或非首页显示(Nav…...
