边缘计算对现代交通的重要作用
边缘计算之所以重要,是在于即使在5G真正商用之时,可以实现超大带宽(eMBB)的应用场景,但庞大数据量的涌现也就意味着需要在云和端传输过程中找到一个承接点,对数据进行预处理再选择是否上云。
边缘计算应用演进
“现在的4G网络基本能解决80%的传输问题,相比之下,用5G网络只是少了30毫秒的速率。”对于现有应用而言,当前的大部分网络传输都不存在太大问题,5G面临的其实是新应用的适配难题。
“5G在物联时,面临的很大问题将是覆盖率。一旦出现基站没有覆盖到位,就很难保证100%的数据传输,甚至运行过程中有可能存在闪断等问题。此外一个数据包从一端传输到另一端,会有很多重传,不是直接就一定能全部传过去,这还涉及到底层协议。因此有很多实际问题要解决。”该人士补充道,这也是边缘计算在5G时代角色越来越重要的原因。
5G从网络架构上会有整体变化。简言之,5G网络是通过SDN(软件定义网络)/NFV(网络功能虚拟化)等方式重构的网络架构。其本身在网络边缘就有基础架构设备或服务器,可以直接通过软件定义的方式,把数据中心的能力迁移到网络边缘上,且可以根据网络的需求量,动态调整边缘计算的能力。
当前用户对于物联网数据的处理,到底放在数据中心、传输之前还是边缘端,实际上诉求是各占三分之一。不过该机构预计,未来随着边缘层上具备更多分析、AI的能力,将促使这些分析功能在边缘层和核心层之间达到平衡。
边缘计算——智能交通的末梢神经
在可预见的未来有两个行业的快速发展是非常明确的,一个是通讯行业,另一个就是交通行业,因为社会的快速发展带来的是更多的信息的和物理上的交流,信息的交流靠通讯、物理的交流靠交通。因此,作为最先进通讯技术与交通技术的结合,智能交通领域一直是社会一个关注的焦点。
在过去的十年中,智能交通让几何级数增长的城市车辆获取了实时路况信息,让举世瞩目的中国高铁保持着高速运转,让远洋航海中的水手便捷地同家人实时通话。但是,许多业内期待的如自动驾驶、轨道交通无人值守等技术依然还不能完全实现。
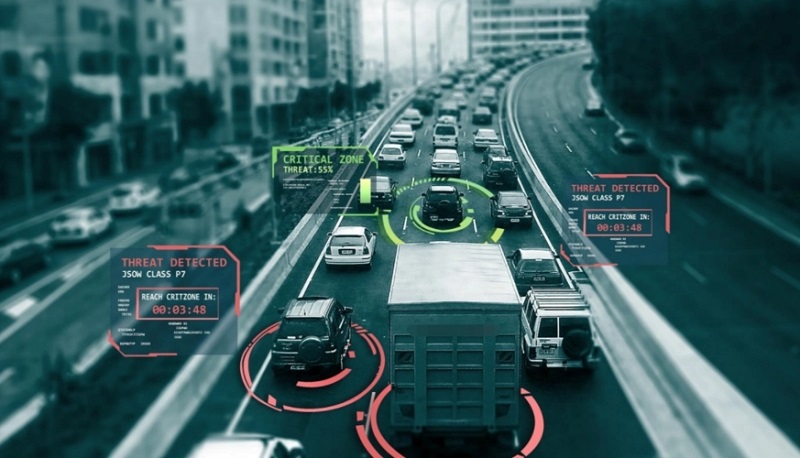
伴随着新技术的发展,我们逐渐步入全联接的“智能社会”,物联网领域的新技术“边缘计算”被应用在智能交通领域。这为长期困扰行业发展的诸多难题迎来了解决的希望。边缘计算是指通过物联网络将计算能力和服务部署在网络的边缘,向附近的终端、感应器、用户提供通讯和计算服务,解决物联网系统在高分布式场景下的海量异构联接、业务实时性、业务智能性、数据互操作性以及安全和隐私保护等挑战。通俗来说,在未来的智能交通应用环境中,“云计算”就相当于智能设备的大脑,处理相对复杂的进程;而“边缘计算”就相当于智能设备的神经末梢,进行一些“下意识”的反应。
边缘计算的到来让智能交通更具安全性。无论是公路、铁路、海运还是航空,安全都是交通行业最为重要的事情。例如最近各大科技公司都不遗余力进行投入的自动驾驶技术迟迟不能应用的最重要原因也是其不能确保上路的绝对安全。“边缘计算”的到来,对这些问题的解决带来了很大帮助。如同人类一样,我们对危险的第一道反应通常不是经过大脑,而是“下意识”的。例如,一辆自动驾驶的汽车在面临危险需要及时停止的时候,如果其还需把数据上传到“云端”,通过计算得出停止的命令,再传送到汽车,汽车再作出反应。那么就不如让车辆本身也具备一定的计算能力,来处理这一问题。同时,我们还可以预想这样一个场景,突发的自然灾害、信号干扰或技术故障使得某一区域自动驾驶的汽车、列车陷入无网络状态。那么,它们就只能依靠边缘计算赋予其的计算能力作出“下意识”的反应,才能确保其安全。
相关文章:

边缘计算对现代交通的重要作用
边缘计算之所以重要,是在于即使在5G真正商用之时,可以实现超大带宽(eMBB)的应用场景,但庞大数据量的涌现也就意味着需要在云和端传输过程中找到一个承接点,对数据进行预处理再选择是否上云。 边缘计算应用演…...

Python桥接模式介绍、使用
一、Python桥接模式介绍 概念: Python桥接模式(Bridge Pattern)是一种软件设计模式,用于将抽象部分与其实现部分分离,使它们可以独立地变化。 它可以通过使用桥接接口来创建一个桥接对象来连接抽象和实现部分。 功能…...

ChatGPT在知识图谱的构建和更新中的应用如何?
ChatGPT在知识图谱的构建和更新中具有重要的应用潜力。知识图谱是一种用于表示和存储结构化知识的图形化数据模型,通常由实体、属性和关系组成。知识图谱的构建和更新是一个复杂而关键的过程,涉及知识的收集、组织、链接和推理。ChatGPT作为一种预训练语…...
JS正则表达式:常用正则手册/RegExp/正则积累
一、正则基础语法 JavaScript 正则表达式 | 菜鸟教程 JS正则表达式语法大全(非常详细) 二、使用场景 2.1、校验中国大陆手机号的正则表达式 正则 /^1[3456789]\d{9}$/解释 序号正则解释1^1以数字 1 开头2[3456789]第二位可以是 3、4、5、6、7、8、…...

自动化测试框架unittest与pytest的区别!
引言 前面文章已经介绍了python单元测试框架,大家平时经常使用的是unittest,因为它比较基础,并且可以进行二次开发,如果你的开发水平很高,集成开发自动化测试平台也是可以的。而这篇文章主要讲unittest与pytest的区别&…...
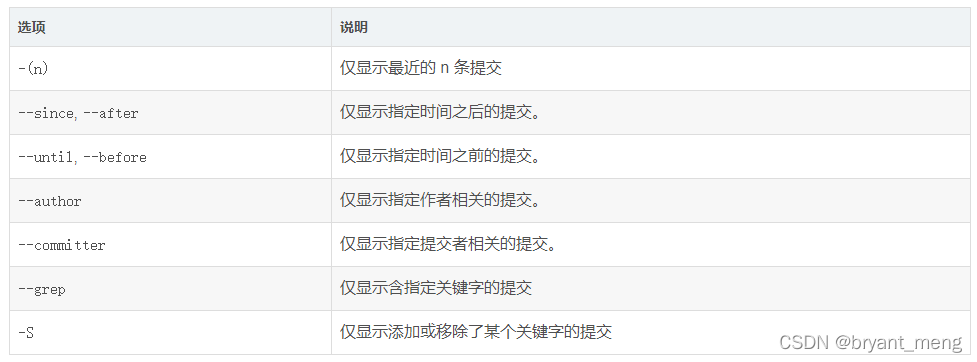
【Git】
学习来自于: 女朋友乱用Git,差点把我代码删了。。。 一些常用的Git 知识点整理 关于Git这一篇就够了 Git基本命令大全 30分钟精通Git,学不会来找我 Git 版本管理 | 莫烦PYTHON Git 代码版本管理教程 文章目录 【前言】集中式与分布式的…...

[论文笔记] CLRerNet: Improving Confidence of Lane Detection with LaneIoU
Honda, Hiroto, and Yusuke Uchida. “CLRerNet: Improving Confidence of Lane Detection with LaneIoU.” arXiv preprint arXiv:2305.08366 (2023). 2023.05 出的一篇车道线检测的文章, 效果在CULane, CurveLanes SOTA 文章目录 简介LaneIoULineIoU存在问题为什么使用LaneIo…...

LeetCode|backtracking|review:40. 131. 93. 47. 332. | 37. Sudoku Solver
复习: 40. Combination Sum II [1,1,2,3]中,答案里有[1,1,2], 但是不能有两个[1,2,3] 131. Palindrome Partitioning 每个for都是在给定的start之后找一个palindrome。当start 93. Restore IP Addresses forloop每次loop都是在给定的start的后三个数…...

被泼冷水后,谁能超越微服务?
历史总会重演。一切刚过去的,又会被重新提起。开源项目Codename One的联合创始人Shai,曾是Sun Microsystems开源LWUIT项目的共同作者,参与了无数开源项目。作为最早一批Java开发者,最近感慨道:单体,又回来了…...
多线程(JavaEE初阶系列5)
目录 前言: 1.什么是定时器 2.标准库中的定时器及使用 3.实现定时器 结束语: 前言: 在上一节中小编给大家介绍了多线程中的两个设计模式,单例模式和阻塞式队列模式,在单例模式中又有两种实现方式一种是懒汉模式&a…...

Minimum Snap闭式求解相关公式推导
文章目录 1 M i n i m u m Minimum Minimum S n a p Snap Snap闭式求解的推导1.1 二次规划等式约束构建1.2 求 d d d1.3 转成无约束优化问题 1 M i n i m u m Minimum Minimum S n a p Snap Snap闭式求解的推导 可以看看我的这几篇Blog1,Blog2,Blog…...
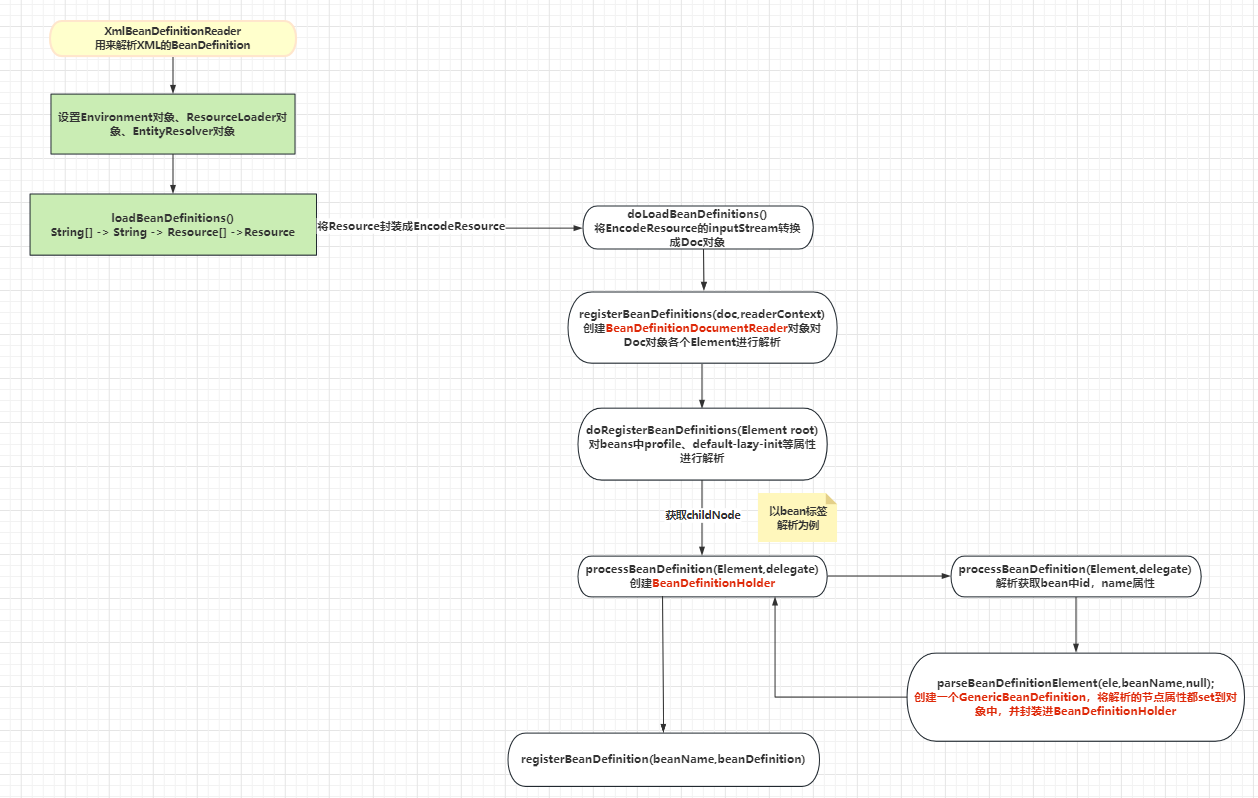
Spring源码(五)— 解析XML配置文件(一) bean标签解析流程
前面几章的内容已经介绍了BeanFactory创建前的准备工作,以及加载XML配置文件前的准备的步骤。本章会着重介绍解析XML的步骤。 registerBeanDefinitions 前几个方法不做过多的赘述,着重看registerBeanDefinitions方法中解析XML的步骤。 public int regi…...

隐私政策声明
http://lxfamn.cn/tools 我们注重对您个人隐私的保护。有时候我们需要某些信息才能为您提供您请求的服务,本隐私声明解释了这些情况下的数据收集和使用情况。本隐私声明适用于本网站的所有相关服务。如果您访问本网站、使用本网站的任何服务,那么您便接受…...

Flutter 最佳实践和编码准则
Flutter 最佳实践和编码准则 视频 前言 最佳实践是一套既定的准则,可以提高代码质量、可读性和可靠性。它们确保遵循行业标准,鼓励一致性,并促进开发人员之间的合作。通过遵循最佳实践,代码变得更容易理解、修改和调试ÿ…...
LangChain Agents深入剖析及源码解密上(一)
LangChain Agents深入剖析及源码解密上(一) LangChain Agents深入剖析及源码解密上 Agent工作原理详解 本节会结合AutoGPT的案例,讲解LangChain代理(Agent)为核心的内容。我们前面已经谈了代理本身的很多内容,也看了绝大部分的源代码,例如:ReAct的源代码,还有mrkl的源代…...
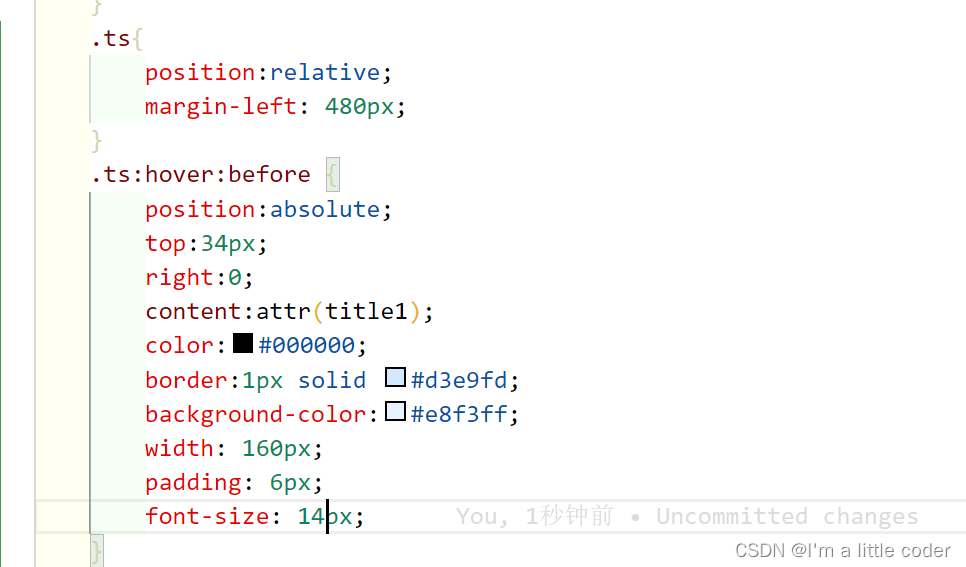
css定义超级链接a标签里面的title的样式
效果: 代码: 总结:此css 使用于任何元素,不仅仅是a标签!...
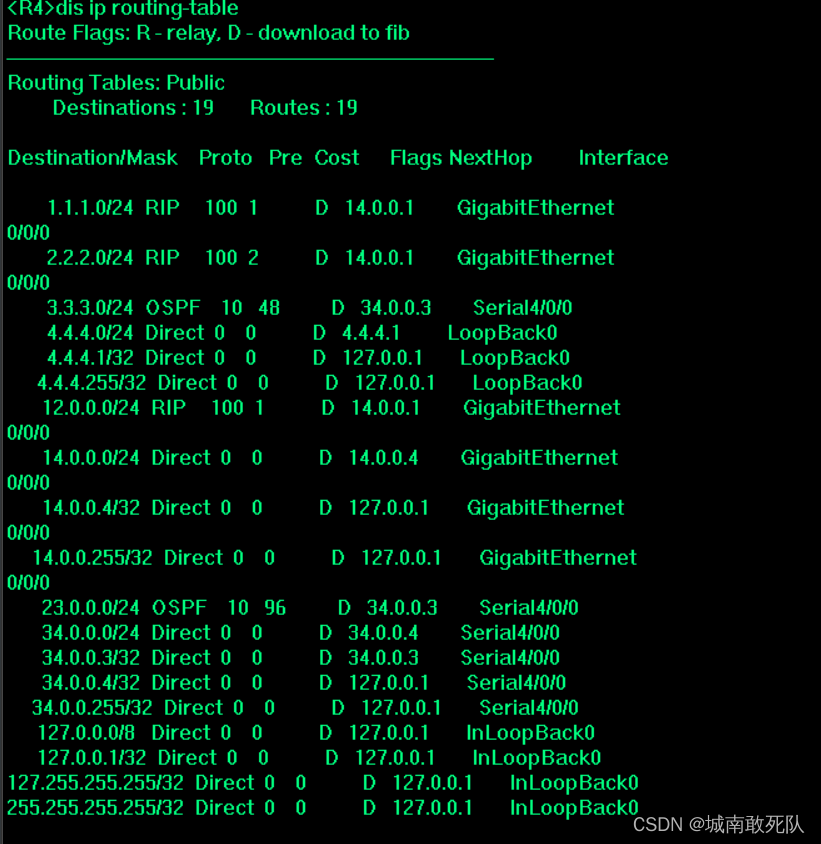
hcip——路由策略
要求: 基础配置 AR1 [R1]int g 0/0/0 [R1-GigabitEthernet0/0/0]ip add 12.0.0.1 24[R1-GigabitEthernet0/0/0]int g 0/0/1 [R1-GigabitEthernet0/0/1]ip add 14.0.0.1 24[R1]int loop0 [R1-LoopBack0]ip add 1.1.1.1 24[R1]rip 1 [R1-rip-1]vers 2 [R1-rip-1]net…...
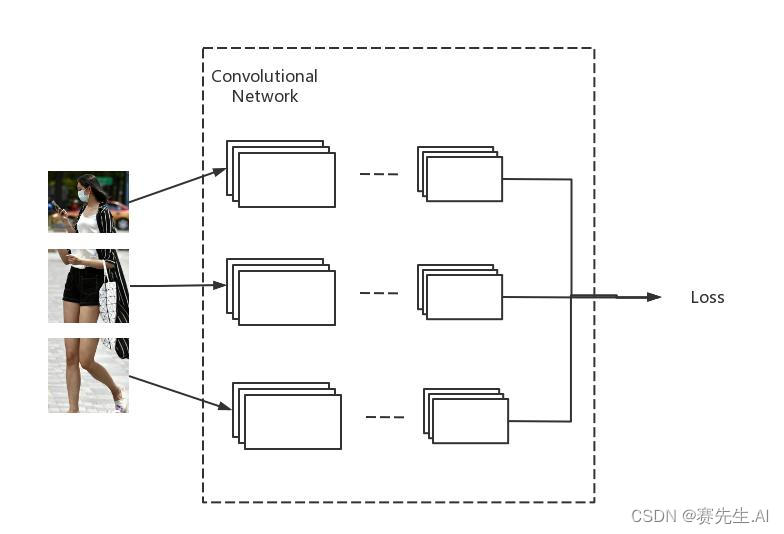
ReID网络:MGN网络(1) - 概述
Start MGN 1. 序言 现代基于感知的信息中,视觉信息占了80~85%。基于视觉信息的处理和分析被应用到诸如安防、电力、汽车等领域。 以安防市场为例,早在2017年,行业咨询公司IHS Market,我国在公共和私人领域安装有摄像头约1.76亿…...
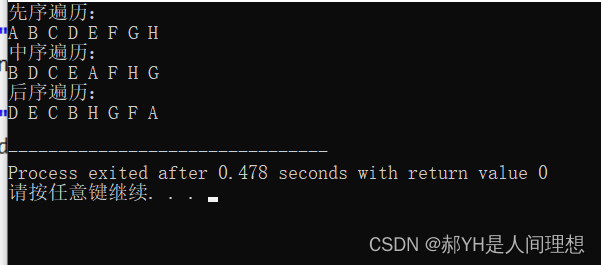
C++数据结构笔记(10)递归实现二叉树的三序遍历
对于三种遍历方式来说,均为先左后右!区别在于根结点的位置顺序 先序遍历:根——左——右 中序遍历:左——根——右 后序遍历:左——右——根 (所谓先中后的顺序,是指根结点D先于子树还是后于…...
hMailServer-5.3.3-B1879.exe
hMailServer-5.3.3-B1879.exe...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...
