【C#】async和await 续
前言
在文章《async和await》中,我们观察到了一下客观的规律,但是没有讲到本质,而且还遗留了一个问题:
这篇文章中,我们继续看看这个问题如何解决!
我们再看看之前写的代码:
static public void TestWait2()
{var t = Task.Factory.StartNew(async () =>{Console.WriteLine("Start");await Task.Delay(3000);Console.WriteLine("Done");});t.Wait();Console.WriteLine("All done");}static public void TestWait3()
{var t = Task.Run(async () =>{Console.WriteLine("Start");await Task.Delay(3000);Console.WriteLine("Done");});t.Wait();Console.WriteLine("All done");
}
当时问题是,为啥 Task.Factory.StartNew 可以看到异步效果,而Task.Run中却是同步效果。
那其实是因为,Task.Factory.StartNew 返回的 t.Wait(); 它没卡住主线程,而Task.Run的 t.Wait();它卡住了。
那为啥,Task.Factory.StartNew没卡住呢?
这是应为 Task.Factory.StartNew 返回的变量 t 他是Task< Task >类型!
如果,Task.Run 返回的是Task类型,如果我们改成Task.Factory.StartNew,那么它 返回的类型就是Task<Task< int >>
在.Net4.0中提供一个Unwrap方法,用于将Task<Task< int>>解为Task< int>类型,所以如果代码改为:
static public async void Factory嵌套死等()
{Console.WriteLine($"Factory不嵌套死等{getID()}");var t = Task.Factory.StartNew(async() =>{Console.WriteLine($"Start{getID()}");await Task.Delay (1000);Console.WriteLine($"Done{getID()}");}).Unwrap();t.Wait();Console.WriteLine($"All done{getID()}");
}
那么此时 t.Wait(); 也能卡死主线程。
其实Task.Run(.net4.5引入) 是在 Task.Factory.StartNew(.net4.0引入) 之后出现的,Task.Run是为了简化Task.Factory.StartNew的使用。
t.Wait() 和 await t;
现在我从另一个角度分析问题。
使用 Task.Run,能不能达到异步的效果? 答案是肯定的!
不过,我们此时不应该使用 t.Wait(); 而是应该是 await t;
static public async void Run嵌套Await()
{Console.WriteLine($"Run嵌套Await{getID()}");var t = Task.Run(async () =>{Console.WriteLine($"Start{getID()}");await Task.Delay(1000);Console.WriteLine($"Done{getID()}");});await t;Console.WriteLine($"All done{getID()}");
}
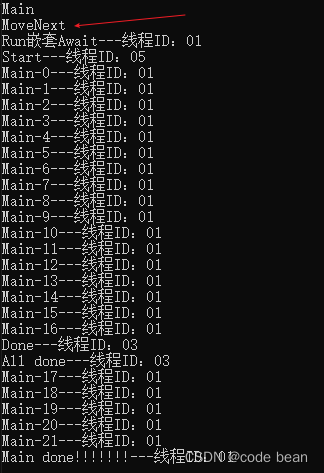
这样的话就实现了异步效果。
await 是如何实现异步的
这里我们可以进一步分析一下。
“1” 是主线程的ID “5” 是 task 启的子线程 ID。
我发现All done 在 Done 后面执行的,这是应为 await t; 把主线程"遣返了"
而await t; 之后的代码(也就是All done 这句话的打印)是由子线程5接着完成的。
整个流程是这样的,当编译时,编译器看到了函数使用了 async 关键字,那么整个函数将被转换为一个带有状态机的函数,反编译后发现函数名称变为MoveNext。
当主线程执行到子函数时,遇到 await 那么此时 主线程就会返回(跳出整个子函数,去执行下一个函数),MoveNext呢就会切换状态机(由于状态机已经切换,下次MoveNext在被调用时,就会从await 处向下执行)。
不过,从现象看await 之后的代码,不是主线程调用了,而是Task的子线程。子线程会再次调用MoveNext,并且进入一个新的状态机。
这里就有一个结论,当主线程进入一个子函数,遇到await机会从函数直接返回,函数中以下的代码交给新的子线程执行。
为了证明一这一点,我又写了一个程序:
static public async Task AsyncInvoke()
{await Task.Run(() =>{Console.WriteLine($"This is 1 ManagedThreadId={Thread.CurrentThread.ManagedThreadId.ToString("00")}");Thread.Sleep(1000);});Console.WriteLine($"1{getID()}");await Task.Run(() =>{Console.WriteLine($"This is 2 ManagedThreadId={Thread.CurrentThread.ManagedThreadId.ToString("00")}");Thread.Sleep(1000);});Console.WriteLine($"2{getID()}");await Task.Run(() =>{Console.WriteLine($"This is 3 ManagedThreadId={Thread.CurrentThread.ManagedThreadId.ToString("00")}");Thread.Sleep(1000);});Console.WriteLine($"3{getID()}");await Task.Run(() =>{Console.WriteLine($"This is 4 ManagedThreadId={Thread.CurrentThread.ManagedThreadId.ToString("00")}");Thread.Sleep(1000);});Console.WriteLine($"4{getID()}");
}执行效果如下:
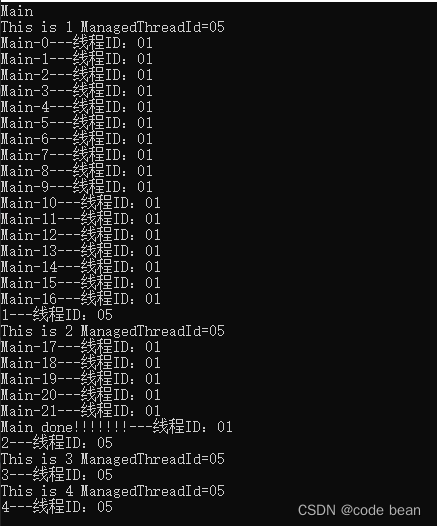
你会发现不过一个函数里面有多少个await ,主线程遇到一个await就返回了,就跳出这个函数去执行其他的函数了。
函数剩下的await 后面的都是由子线程完成的!多个await 只是多个几个状态机而已。
所以在一个函数中,如果有个多个await ,除了第一个后面的都和主线程无关。
这里又出现了一个新的问题,为啥后面的线程ID都是5?这个其实不一定的,我重新跑了一次:
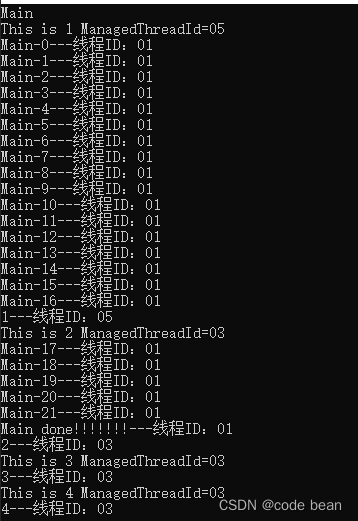
这次发现出现了两个子线程号 3 和 5,这是应为 Task 背后有个 线程池。Task 被翻译为任务,单纯的线程是指的Thread。
Task 启动后,使用哪个线程是由背后的线程池提供,而这个线程池是由.net进行维护。包括回调什么时候发生都是由线程池中的一个线程通知Task对象!await 操作符 其实是 调用 Task对象的 ContinueWith,所以上面这段代码也可以这么写:
/// <summary>
/// 回调式写法
/// </summary>
public void TaskInvokeContinue()
{Task.Run(() =>{Console.WriteLine($"This is 1 ManagedThreadId={Thread.CurrentThread.ManagedThreadId.ToString("00")}");Thread.Sleep(1000);}).ContinueWith(t =>{Console.WriteLine($"This is 2 ManagedThreadId={Thread.CurrentThread.ManagedThreadId.ToString("00")}");Thread.Sleep(1000);}).ContinueWith(t =>{Console.WriteLine($"This is 3 ManagedThreadId={Thread.CurrentThread.ManagedThreadId.ToString("00")}");Thread.Sleep(1000);}).ContinueWith(t =>{Console.WriteLine($"This is 4 ManagedThreadId={Thread.CurrentThread.ManagedThreadId.ToString("00")}");Thread.Sleep(1000);});//不太爽---nodejs---回调式写法,嵌套是要疯掉
}
这就进一步体现了 await 用同步的方式,写异步的代码。
能实现这个的原因就是,函数已经被改造成一个状态机了。
到这里,我就把上次坑给填上了!下次我们在一起掰扯掰扯Task的一些有意思的用法。
小结
我觉得最重要的一点就是:
主线程遇到一个await就返回了,如何理解这个返回?
返回就是跳出这个函数,和这个函数没有半毛钱关系了,去执行其他下面的函数了。
该函数剩下的await后面的部分 都是由线程池中的子线程完成的!
理解这一点,有助于我们对异步代码的编写!
2023年7月29日 更新 (一次Debug的分享)
昨天才写完这篇文章,今天就发现之前的写的一段代码有问题。没想到这么快就用上了~~(笑哭)
程序大概是这样的。我有一个主线程,里面有两个函数A和B,A和B实现了 async await 。
A和B里有一句 await tcpcli.SendAsync(str) 这句异步代码, 大致代码如下:
while(true)
{await A(){....bool b = await tcpcli.SendAsync(str);}await B(){....await tcpcli.SendAsync(str);}
}
正常情况下,这样没啥问题。程序都是正常跑。但是当Tcp服务那边反应延时的时候,就会出问题。
运行到 bool b = await tcpcli.SendAsync(str); 时,按照之前的结论,主线程都是直接返回的,就会直接执行B
然后再接着执行A,但是如果bool b = await tcpcli.SendAsync(str); 依然还在等待,之线程还是会返回的,
此时会再次开一个新的线程,导致多个线程并发,但是我这里其他逻辑并发的话是会有问题的(比如写Modbus的一个寄存器)。
所以,一旦 tcpcli.SendAsync(str)卡住了,逻辑就出问题了!
既然逻辑不能并发,我当时为啥不直接用同步的方式呢?其实原因是当时我不知道如何用同步的方式获取返回值。
我当时 调用 tcpcli.SendAsync(str).Wait(); 时发现这个Wait()返回值是空,但是我又需要返回值,所以就用了
bool b = await tcpcli.SendAsync(str); 那其实如果想用同步的方式获取返回值,应该使用:
bool b = tcpcli.SendAsync(str).GetAwaiter().GetResult();
所以,最后改程序为:
while(true)
{await A(){....bool b = tcpcli.SendAsync(str).GetAwaiter().GetResult();}await B(){....tcpcli.SendAsync(str).Wait();}
}
相关文章:

【C#】async和await 续
前言 在文章《async和await》中,我们观察到了一下客观的规律,但是没有讲到本质,而且还遗留了一个问题: 这篇文章中,我们继续看看这个问题如何解决! 我们再看看之前写的代码: static public void TestWait2() {var t…...
)
【Matlab】基于粒子群优化算法优化BP神经网络的数据回归预测(Excel可直接替换数据)
【Matlab】基于粒子群优化算法优化 BP 神经网络的数据回归预测(Excel可直接替换数据) 1.模型原理2.数学公式3.文件结构4.Excel数据5.分块代码5.1 fun.m5.2 main.m6.完整代码6.1 fun.m6.2 main.m7.运行结果1.模型原理 基于粒子群优化算法(Particle Swarm Optimization, PSO)…...

QPainter绘制雷达界面
文章目录 功能实现定义的结构体定义的函数效果图gitee源码链接 功能实现 相较于上一版,这一版添加的功能有: 1、自适应窗口 2、扫描方式(圆周扫描、扇形扫描(指定起始角度和结束角度)) 3、扫描方向&#x…...
flutter:BottomNavigationBar和TabBar
区别 BottomNavigationBarr和TabBar都是用于创建导航栏的组件,但它们有一些区别。 位置不同:BottomNavigationBar通常位于屏幕底部,用于主要导航;而TabBar通常位于屏幕顶部或底部,用于切换不同的视图或页面。 样式不…...

【图论】Prim算法
一.介绍 Prim算法是一种用于解决最小生成树问题的贪心算法。最小生成树问题是指在一个连通无向图中找到一个生成树,使得树中所有边的权重之和最小。 Prim算法的基本思想是从一个起始顶点开始,逐步扩展生成树,直到覆盖所有顶点。具体步骤如下…...

第九十二回 在Flutter中解析JSON数据
文章目录 概念介绍解析方法convert库插件工具 示例代码经验总结 我们在上一章回中介绍了"对dio库进行封装"相关的内容,本章回中将介绍 如何在Flutter中解析JSON数据.闲话休提,让我们一起Talk Flutter吧。 概念介绍 我们在前面章回中介绍了通…...
银河麒麟安装mysql数据库(mariadb)-银河麒麟安装JDK-银河麒麟安装nginx(附安装包)
银河麒麟离线全套安装教程(手把手教程) 1.银河麒麟服务器系统安装mysql数据库(mariadb) 2.银河麒麟桌面系统安装mysql数据库(mariadb) 3.银河麒麟服务器系统安装JDK 4.银河麒麟桌面系统安装JDK 5.银河麒麟…...
文件上传
js绕过 打开网页尝试上传一句话木马,发现只能上传图片文件 审计源代码,发现使用一个checkfile函数js对文件类型进行了屏蔽 于是我们修改网页代码,去除返回值的检查函数 checkFile() 上传成功,使用蚁剑连接 连接成功 .htaccess绕…...
tinkerCAD案例:22. Backpack Zipper Pull 背包拉链头
tinkerCAD案例:21. Custom Stamp 定制印章 原文 tinkerCAD案例:22. Backpack Zipper Pull 背包拉链头 Lesson Overview: 课程概述: Now we’re going to make a zipper pull! 现在我们要做一个拉链头! Your backpack, howev…...
Unity 性能优化四:UI耗时函数、资源加载、卸载API
UI耗时函数 1.1 Canvas.SendWillRenderCanvases 这个函数是由于自身UI的更新,产生的耗时 1. 这里更新的是vertex 属性,比如 color、tangent、position、uv,修改recttransform的position、scale,rotation并不会导致顶点属性改变…...
【Linux】用户相关内容
如果命令ll 出现以上信息,UID为具体的数字,代表之前UID为502的用户被删除了。 更改目录或文件所属用户和所属组 在Linux中,创建一个文件时,该文件的拥有者都是创建该文件的用户。 更改所属用户 chown 用户名 文件名/目录名 更…...
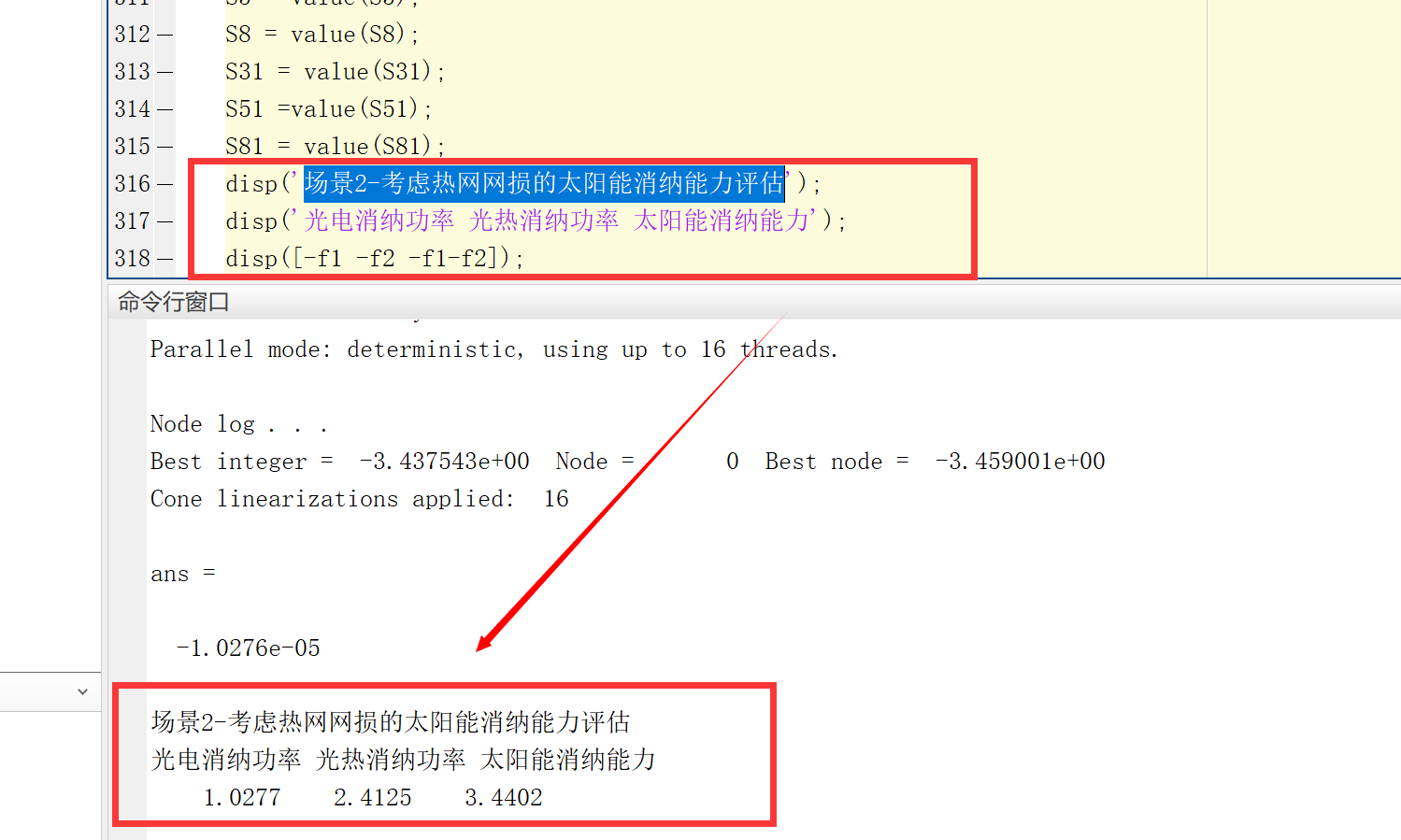
基于多场景的考虑虑热网网损的太阳能消纳能力评估研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

【动态规划part10】| 121.买卖股票的最佳时机、122.买卖股票的最佳时机II
目录 🎈LeetCode121. 买卖股票的最佳时机 🎈LeetCode122.买卖股票的最佳时机II 🎈LeetCode121. 买卖股票的最佳时机 链接:121.买卖股票的最佳时机 给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定…...

java 页面html常用写法总结
(注意:本文章默认base html中已经引入bootstrap.min.css、style.css等css样式) input :输入标签 <#input required"必填" id"cycle" name"周期" underline"true" style"width:75%" itype&quo…...
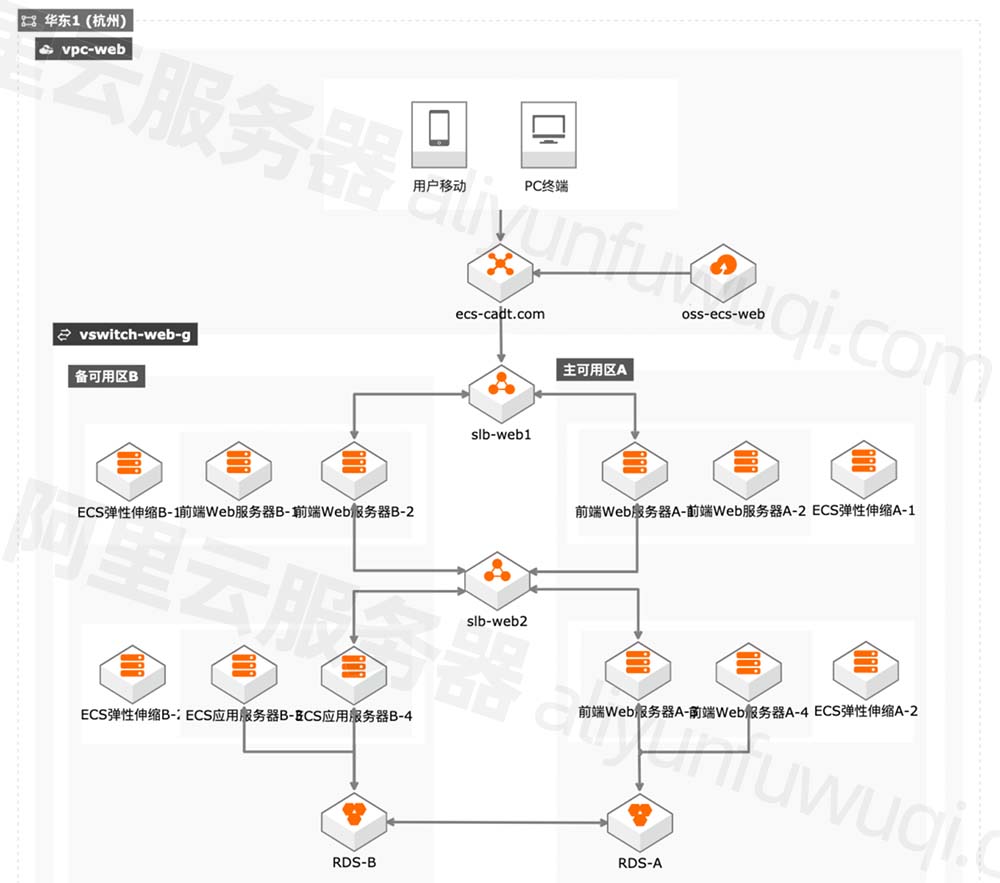
阿里云服务器全方位介绍_优势_使用_租用费用详解
阿里云服务器全方位介绍包括云服务器ECS优势、云服务器租用价格、云服务器使用场景及限制说明,阿里云服务器网分享云服务器ECS介绍、个人和企业免费试用、云服务器活动、云服务器ECS规格、优势、功能及应用场景详细你说明: 目录 什么是云服务器ECS&…...
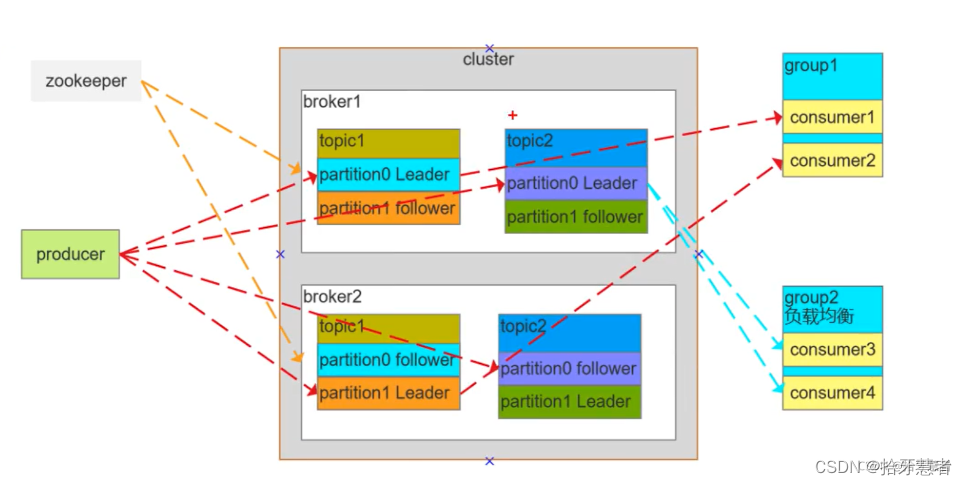
【Kafka】常用操作
1、基本概念 1. 消息: Kafka是一个分布式流处理平台,它通过消息进行数据的传输和存储。消息是Kafka中的基本单元,可以包含任意类型的数据。 2. 生产者(Producer): 生产者负责向Kafka主题发送消息。它将消息…...
【Spring框架】SpringBoot配置文件
目录 配置文件作用application.properties中午乱码问题:配置文件里面的配置类型分类SpringBoot热部署properties基本语法properties配置文件的优缺点:yml配置文件说明yml基本语法配置对象properties VS yml 配置文件作用 整个项⽬中所有重要的数据都是在…...
部署问题集合(十八)Windows环境下使用两个Tomcat
下载Tomcat Tomcat镜像下载地址:https://mirrors.cnnic.cn/apache/tomcat/进入如下地址:zip的是压缩版,exe是安装版 修改第二个Tomcat配置文件 第一步:编辑conf/server.xml文件,修改三个端口,有些版本改…...

数据结构问答8
查找 1. 一些基本概念 关键字:能唯一标识该元素 查找:给定值k,在含n个元素的表中找出关键字==k的元素。找到返回其位置信息,否则返回-1。 动、静态查找表:查找同时对表进行修改(插入、删除等),相应的表为动态,否则为静态。 内、外查找:整个查找过程在内存中进行…...

行为型设计模式之观察者模式【设计模式系列】
系列文章目录 C技能系列 Linux通信架构系列 C高性能优化编程系列 深入理解软件架构设计系列 高级C并发线程编程 设计模式系列 期待你的关注哦!!! 现在的一切都是为将来的梦想编织翅膀,让梦想在现实中展翅高飞。 Now everythi…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

