01背包
动态规划解题步骤:
动态规划问题,一般从三个步骤进行考虑。
步骤一:集合及集合的状态。
所谓的集合,就是一些方案的集合。
用 g[i][j] 表示从前 i 种物品中进行选择,且总体积不大于 j 的各个选法获得的价值的集合。注意,g[i][j] 是个集合,表示一堆数:所有可能选出的价值。
例如 g[2][3] 从前 2 种物品中进行选择,且总体积不大于 3 的各个选法获得的价值的集合。选择方案有三种:都不选,价值为 0、选择第 1 个物品,价值为 2、选择第 2 个物品,价值为 4、选择第 1,第 2 个物品,价值为 6。 g[2][3] = {0, 2, 4, 6}。
例如 g[3][4] 从前 3 种物品中进行选择,且总体积不大于 4 的各个选法获得的价值的集合,选择方案有三种:都不选,价值为 0、选择第 1 个物品,价值为 2、选择第 2 个物品,价值为 4、选择第 3 个物品,价值为 4,选择第 1,第 2 个物品,价值为 6,选择第 1,第 3 个物品,价值为 6。 g[3][4] = {0, 2, 4, 4, 6, 6}。
i j 取不同的值,对应不同的 g[i][j],也就是对应不同的集合。
用 f[i][j] 表示从前 i 种物品中进行选择,总体积小于等于 j 所能获得的最大价值, 注意,f[i][j] 是个一个数,是g[i][j] 这个集合中的最大值。很明显,f[i][j] 就是 g[i][j] 中的最大值。i j 取不同的值,就对应不同的 f[i][j],即对应不同的集合的最大值。
例如 f[2][3] 表示从前 2 种物品中进行选择,且总体积不大于 3 的获得的最大价值。f[2][3] = max(g[2][3]) = 6。
例如 f[3][4] 表示从前 3 种物品中进行选择,且总体积不大于 4 的获得的最大价值。f[3][4] = max(g[3][4]) = 6。
g[i][j] 的最大值就是 f[i][j]。
如果我们能把所有集合对应的最大值都求出来,即求出了 f[0][0] ~ f[N][V], f[N][V] 的含义是在前 N 种物品中进行选择,总体积不大于 V 所获得的最大价值,就是我们要找的答案。
注意,我们不需要把各个集合的所有元素都找出来,只需要求出各个集合的最大值就能找到答案。下面就是如何求出各个集合的最大值。
步骤二:状态计算(求某个集合的最大值)。
g[i][j] 是从前 i 个物品中进行选择,且总体积不大于 j 的各个选法获得的价值的集合。
f[i][j] 是从前 i 种物品中进行选择,总体积小于等于 j 所能获得的最大价值。
f[i][j] 是集合 g[i][j] 的最大值。
所谓的状态计算是指,如何将 f[i][j] 算出来。
如果把各个集合 g[i][j] 的状态 f[i][j] 求出来, f[N][V] 就是要找的答案。
对于上面的例题,g[2][3] 表示从前 2 种物品中选择,总体积小于等于 3 的所有选择方案获得的价值的集合。
选择方案有 三 种:方案1. 只选物品1,价值为 2。 方案2. 只选物品 2,价值为 4。方案3. 同时选物品 1 和物品 2,价值为 6。
g[i][j] = {2, 4, 6}。f[i][j] 为该集合中的最大值 6。
为了求出f[i][j],我们可以使用下面的方法。
将 g[i][j] 这个集合划分成互斥的 A B 两部分。
A 部分是选法中不包含第 i 件物品。B 部分是选法中包含第 i 件物品。只要将 A 部分的最大值和 B 部分的最大值求出来,两者中较大的值就是 g[i][j] 的最大值,也就是 f[i][j]。。
A 部分,等价于从前 i - 1 件物品中选择,选出的物品总体积小于等于 j 的所有方案获得的价值集合,也就是 g[i - 1][j]。g[i - 1][j]这个集合中的最大值是 f[i - 1][j],所以 A 部分的最大值就是 f[i - 1][j]。
B 部分等价于从前 i 件物品中选择,并且必须选择第 i 件物品,且选出的物品总体积小于等于 j 的所有方案获得的价值集合。
B 部分怎么求呢?直接求不太好求,可以试试曲线救国:
因为 B 部分对应的方案中一定要选择第 i 件物品。这时候有两种情况。
给定的容量能放下第 i 件物品,那么第 i 件物品会占据 vivi 的背包空间,剩下的背包空间为 j - vivi 。可以继续从前 i - 1 种物品中,选出的物总体积小于等 j - vivi的物品放入背包中。
从前 i - 1 种物品中进行选择,选出的物总体积小于等 j - vivi 的方案获得的价值集合为 g[i - 1][j - vivi] 。所以 B 部分的元素为 g[i-1][j - vivi] 中各个元素的值加上 wiwi 。g[i-1][j - vivi] 中的最大值为 f[i-1][j - vivi], 因此 B 部分的最大值为 f[i-1][j - vivi] + wiwi 。
给定的容量不能能放下第 i 件物品,这时候背包里就不能放入第 i 件物品,因此 B 部分就是空集。B 部分的最大值为 0。
例如 g[2][3] 可以划分成两部分,A 部分是不包含第 2 种物品,对应方案1。B部分是包含第 2 种物品,对应方案 2 和方案 3。
A 部分的最大值是 f[2 - 1][3] = f[1][3] = 2。
B 部分的最大值是 f[2 - 1][3 - 2] + w2w2 = f[1][1] + 4 = 6。
所以集合g[2][3] 的最大值 f[2][3] = max(A,B) = max(2, 6) = 6。
通过上面分析,我们可以知道,g[i][j] 可以分成两部分,A 部分是不包含第 i 种物品对应所有选法获的价值的集合,最大值是 f[i - 1][j]。B 部分是包含第 i 种物品对应所有选法获的价值的集合,最大值是 f[i-1][j - vivi] + wiwi 或 0。所以 g[i][j] 的最大值就是在 A 部分的最大值与 B 部分的最大值取个max,也就是:
从计算公式可以看出,f[i][j] 是由 f[i - 1][j -vivi ] 和 wiwi 计算出来的。也就是f[i][j]的值是可以从前面已经计算出的 f 值求出来。如果我们能确定 f[i][j] 的一部分初始值,就能通过该公式,一步步计算得出 f[N][V],也就是我们要找的答案。
步骤三:确定初始值
0 1 背包问题的有些状态是能够直接确定的。
例如 f[0][0]。
f[0][0] 的含义是从前 0 件物品中选择,并且选出的物品总体积小于等于0 时所能得到的最大价值。总体积小于等于 0,说明一种物品都不能选择,因此 f[0][0] = 0。同理 f[1][0] = 0,f[2][0] = 0 ··· f[N][0] = 0。
有了这些初始值,通过 i 从 1 遍历 N,j 从 1 遍历 V,就能一步步求出所有的 f[i][j] 了。
例如求 f[1][1]。f[1][1] = max(A, B) = max{f[0][1],f[0][0] + 2} = max(0,2) = 2。
求 f[1][2]。f[1][2] = max(A, B) = max{f[0][2],f[0][0] + 2} = max(0,2) = 2。
最后 f[N][V] 就是要找的答案。
这时候就可以写代码了:
#include <iostream>
#include <algorithm>using namespace std;const int N = 1010;int n, m;
int v[N], w[N];//v 保存体积,w 保存价值
int f[N][N];//保存所有集合最值状态int main()
{cin >> n >> m;for (int i = 1; i <= n; i ++ )cin >> v[i] >> w[i];for(int i = 0; i <= m; i++)//初始化,前 0 中物品中选择{f[0][i] = 0;}for (int i = 1; i <= n; i ++ ){for (int j = 1; j <= m; j ++){if(v[i] <= j)//能放入第 i 件物品的情况下,求f[i][j]f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + w[i]);else//不能放入第 i 件物品的情况下,求f[i][j]f[i][j] = f[i - 1][j];}}cout << f[n][m] << endl;//f[n][m] 就是答案return 0;
}
优化 动态规划的优化一般都是对代码或者集合最值方程进行一个等价变形。在考虑动态规划问题的时候,一定要先把基本的形式写出来,然后再对它进行优化。
首先,根据优化前的起码,f[i][j] 是从上到下,一行一行这样填满的:
看一下 f[i][j] 的计算公式:f[i][j] = max(A, B)。
只用到了f[i - 1][j],f[i-1][j - vivi] ,即只用到了 f[i - 1] 这一层,并且用到的体积为 j 和 j - vivi ,都是小于等于 j 的。
因此可以从体积为 V 开始,利用f[i - 1]的数据,求解出 f[i][j],把 f[i][j] 放到 f[i -1][j] 的位置上。这样 f 数组就能优化到一维了。
并且,当 背包容量小于 vjvj 的时候,f[i][j] = max{f[i - 1][j],0} = f[i - 1][j]。所以 j 只需要从 V 遍历到 vjvj 即可。
写下代码:
#include <iostream>
#include <algorithm>using namespace std;const int N = 1010;int n, m;
int v[N], w[N];
int f[N];int main()
{cin >> n >> m;for (int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i];for (int i = 1; i <= n; i ++ )for (int j = m; j >= v[i]; j -- )f[j] = max(f[j], f[j - v[i]] + w[i]);cout << f[m] << endl;return 0;
}相关文章:

01背包
动态规划解题步骤: 动态规划问题,一般从三个步骤进行考虑。 步骤一:集合及集合的状态。 所谓的集合,就是一些方案的集合。 用 g[i][j] 表示从前 i 种物品中进行选择,且总体积不大于 j 的各个选法获得的价值的集合。注意&#…...
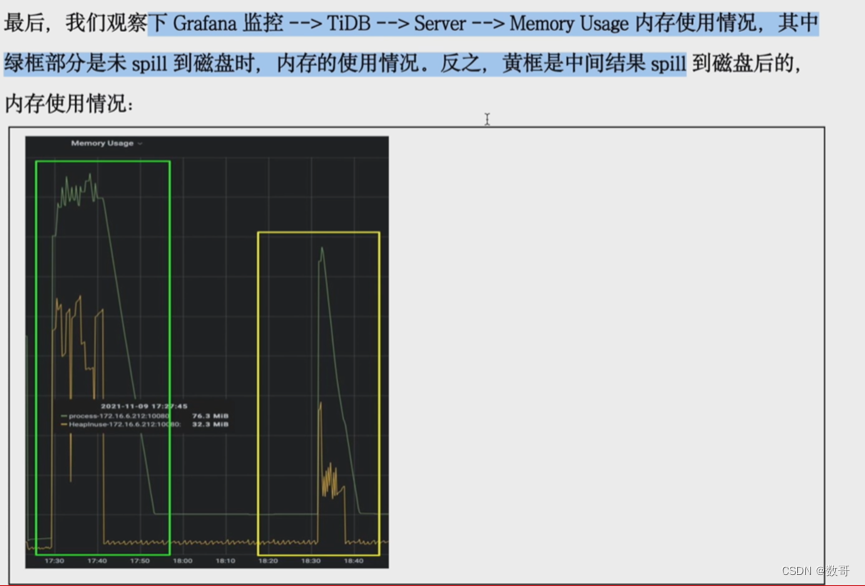
064、故障处理之OMM_TiDB
oom 内存溢出,内存泄漏,相当于TiDB不能用了 TiDB Server OOM对业务的影响 TiDB Server上的业务SQL会失败业务响应时间升高前端体验变差 诊断方法 客户端应用 ERROR 2013(HY000): Lost connection to MySQL Server during query日志 dmesg -T | gr…...

网络设备中的配置文件管理
建立强大网络的第一步是为灾难和网络中断做好准备,许多企业在中断期间遭受损失,因为他们缺乏备份计划并且配置管理不达标,使用配置文件管理工具进行适当的配置文件管理不仅有助于处理网络中断,还有助于优化网络性能。 使用配置文…...
HCIP BGP综合实验
题目 1、AS1存在两个环回,一个地址为192.168.1.0/24该地址不能在任何协议中宣告; 2、AS3中存在两个环回,一个地址为192.168.2.0/24该地址不能在任何协议中宣告,最终要求这两个环回可以互相通讯; 3、AS间的骨干链路I…...

【mysql学习篇】Order by与Group by优化以及排序算法详解
一、Order by与Group by优化 Case1: 分析: 利用最左前缀法则:中间字段不能断,因此查询用到了name索引,从key_len74也能看出,age索引列用在排序过程中,因为Extra字段里没有using filesort 注意…...
【业务功能篇60】Springboot + Spring Security 权限管理 【终篇】
4.4.7 权限校验扩展 4.4.7.1 PreAuthorize注解中的其他方法 hasAuthority:检查调用者是否具有指定的权限; RequestMapping("/hello")PreAuthorize("hasAuthority(system:user:list)")public String hello(){return "hello Sp…...
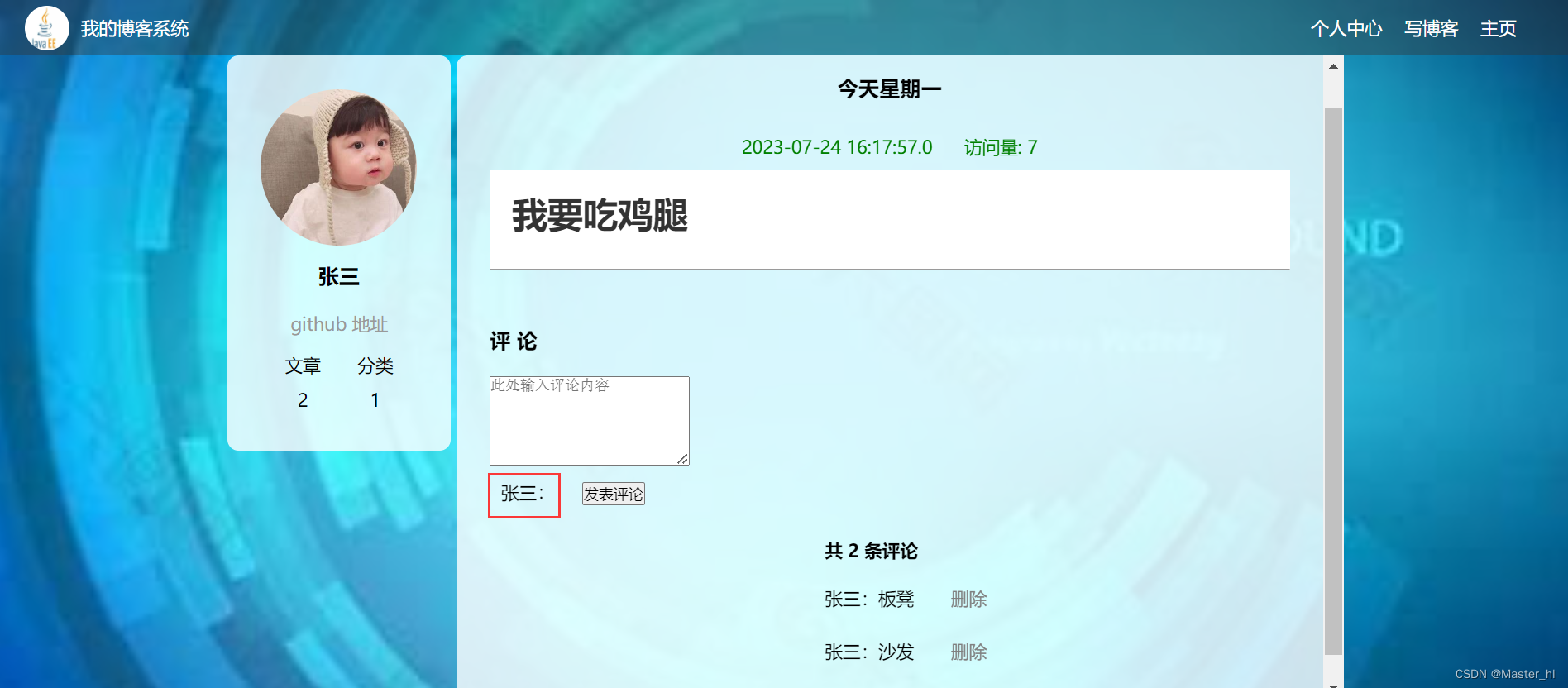
文章详情页 - 评论功能的实现
目录 1. 准备工作 1.1 创建评论表 1.2 创建评论实体类 1.3 创建 mapper 层评论接口和对应的 xml 实现 1.4 准备评论的 service 层 1.5 准备评论的 controller 层 2. 总的初始化详情页 2.1 加载评论列表 2.1.1 实现前端代码 2.1.2 实现后端代码 2.2 查询当前登录用户的…...
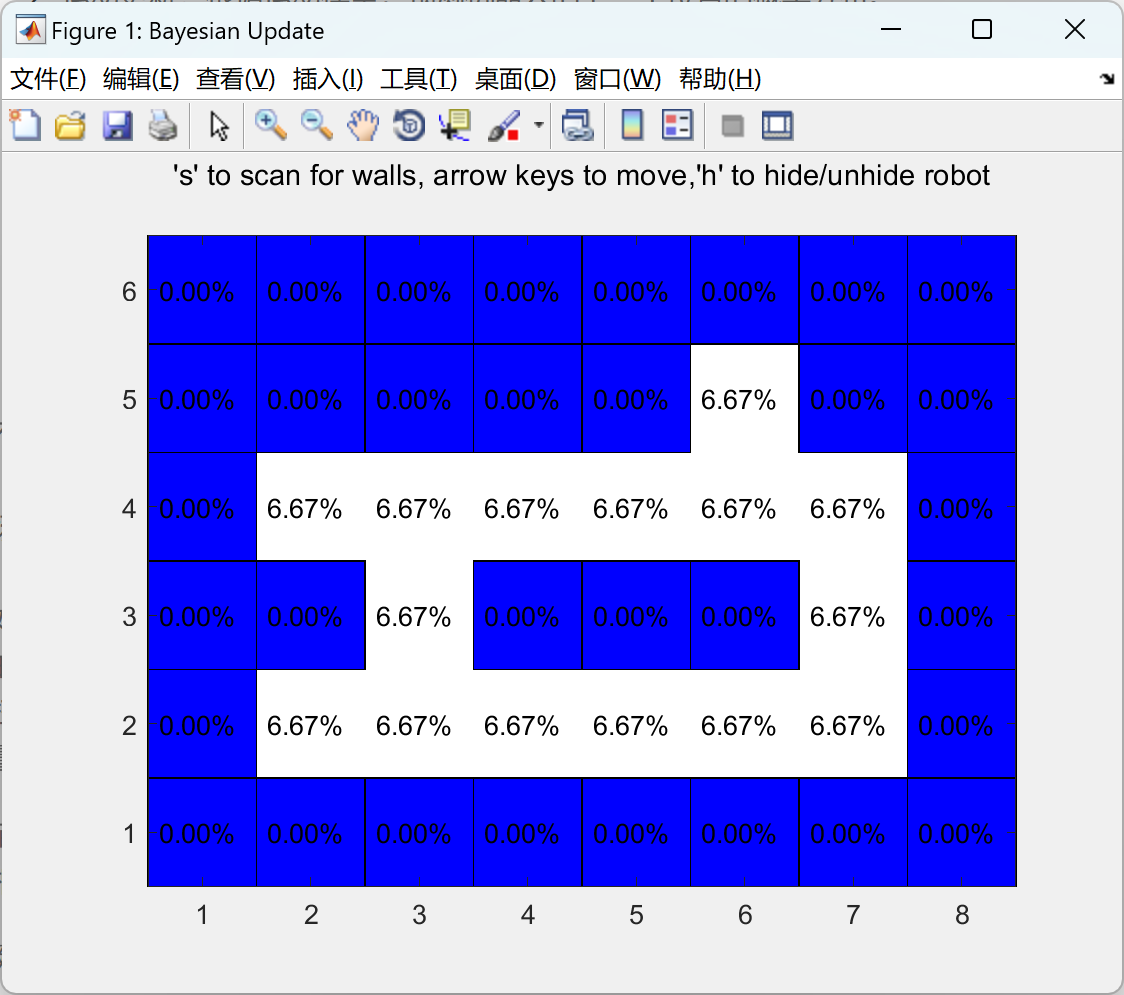
使用贝叶斯滤波器通过运动模型和嘈杂的墙壁传感器定位机器人研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
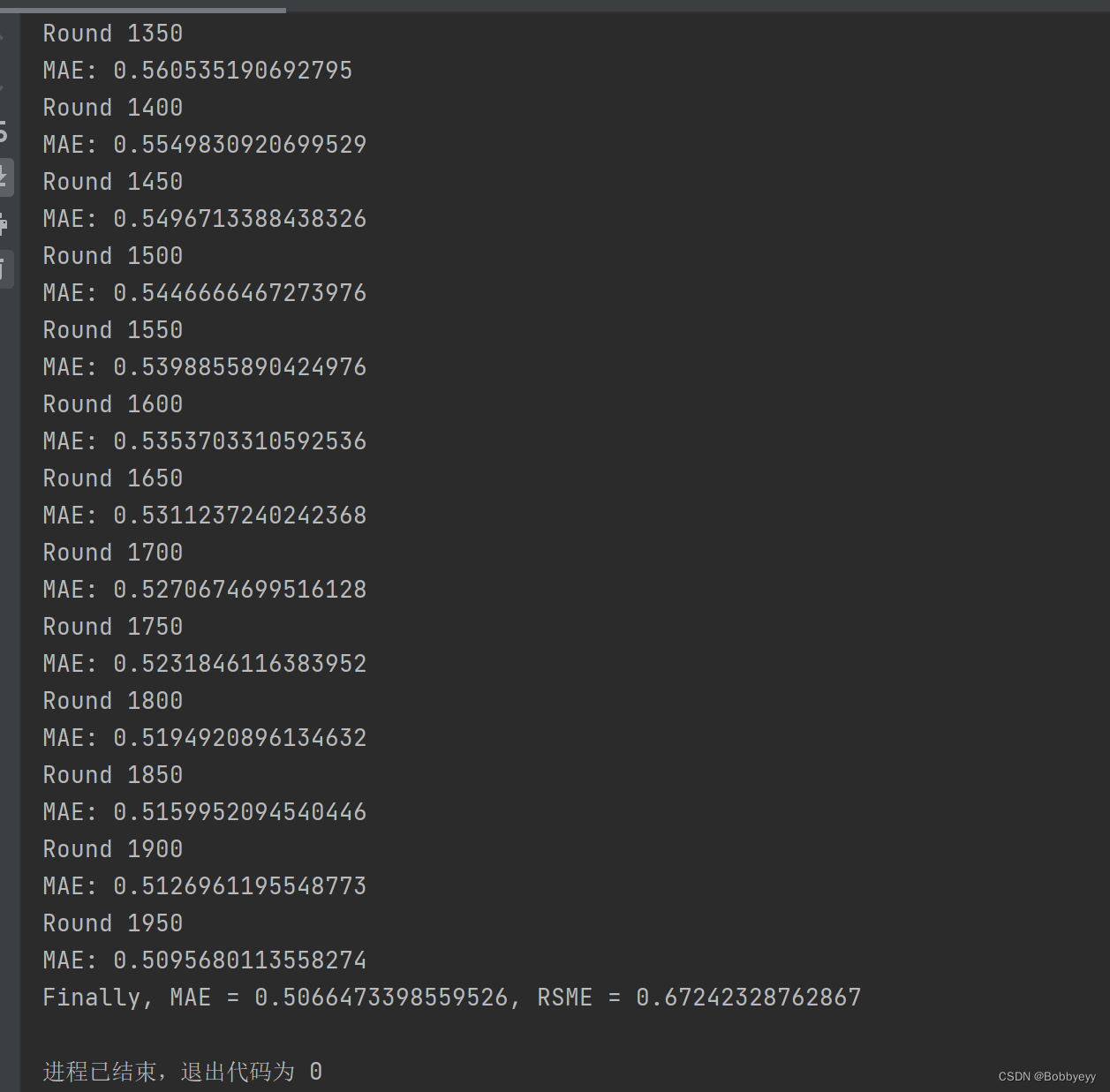
Day 69-70:矩阵分解
代码: package dl;import java.io.*; import java.util.Random;/** Matrix factorization for recommender systems.*/public class MatrixFactorization {/*** Used to generate random numbers.*/Random rand new Random();/*** Number of users.*/int numUsers…...

数据结构:树的存储结构
学习树之前,我们已经了解了二叉树的顺序存储和链式存储,哪么我们如何来存储普通型的树结构的数据?如下图1: 如图1所示,这是一颗普通的树,我们要如何来存储呢?通常,存储这种树结构的数…...
Vue前端渲染blob二进制对象图片的方法
近期做开发,联调接口。接口返回的是一张图片,是对二进制图片处理并渲染,特此记录一下。 本文章是转载文章,原文章:Vue前端处理blob二进制对象图片的方法 接口response是下图 显然,获取到的是一堆乱码&…...
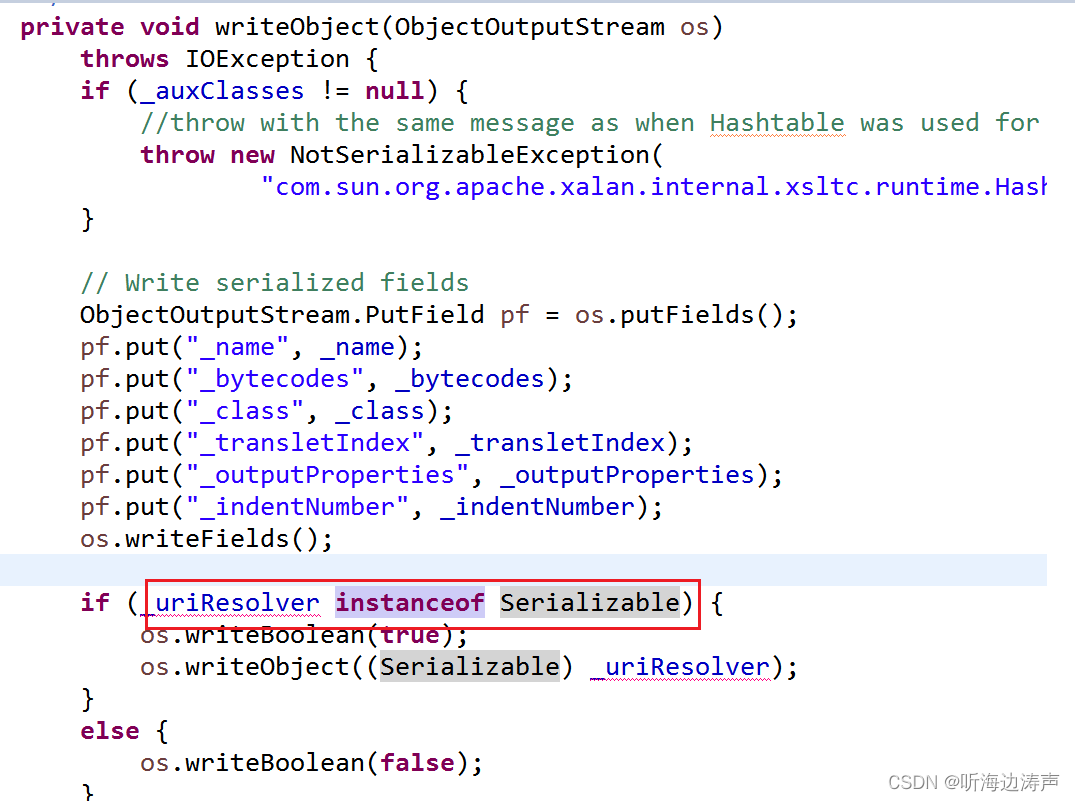
Java的标记接口(Marker Interface)
Java中的标记接口(Marker Interface)是一个空接口,接口内什么也没有定义。它标识了一种能力,标识继承自该接口的接口、实现了此接口的类具有某种能力。 例如,jdk的com.sun.org.apache.xalan.internal.xsltc.trax.Temp…...
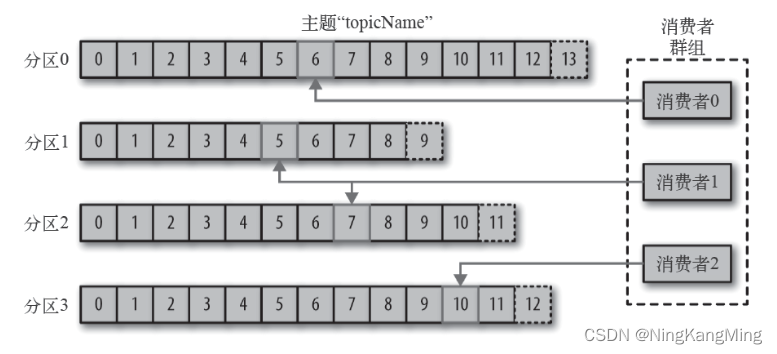
Kafka基础架构与核心概念
Kafka简介 Kafka是由Apache软件基金会开发的一个开源流处理平台,由Scala和Java编写。Kafka是一种高吞吐量的分布式发布订阅消息系统,它可以处理消费者在网站中的所有动作流数据。架构特点是分区、多副本、多生产者、多订阅者,性能特点主要是…...
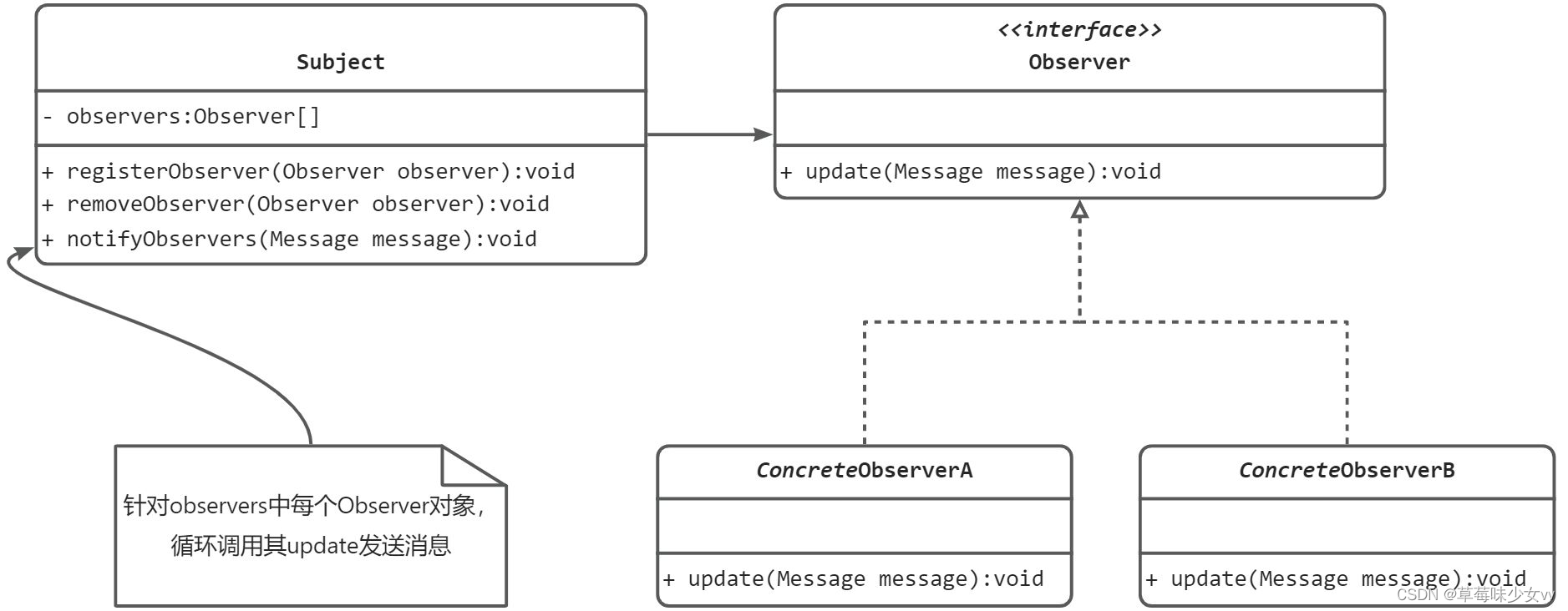
观察者模式与观察者模式实例EventBus
什么是观察者模式 顾名思义,观察者模式就是在多个对象之间,定义一个一对多的依赖,当一个对象状态改变时,所有依赖这个对象的对象都会自动收到通知。 观察者模式也称为发布订阅模式(Publish-Subscribe Design Pattern)࿰…...

科普 | OSI模型
本文简要地介绍 OSI 模型 1’ 2’ 3。 更新:2023 / 7 / 23 科普 | OSI模型 术语节点链路协议网络拓扑 概念作用结构应用层表示层会话层传输层网络层数据链路层物理层 数据如何流动OSI 和TCP/IP 的对应关系和协议参考链接 术语 节点 节点( Node &#…...

redis相关异常之RedisConnectionExceptionRedisCommandTimeoutException
本文只是分析Letture类型的Redis 池化连接出现的连接超时异常、读超时异常问题。 1.RedisConnectionException 默认是10秒。 通过如下可以配置: public class MyLettuceClientConfigurationBuilderCustomizer implements LettuceClientConfigurationBuilderCusto…...

Merge the squares! 2023牛客暑期多校训练营4-H
登录—专业IT笔试面试备考平台_牛客网 题目大意:有n*n个边长为1的小正方形摆放在边长为n的大正方形中,每次可以选择不超过50个正方形,将其合并为一个更大的正方形,求一种可行的操作使所有小正方形都被合并成一个n*n的大正方形 1…...
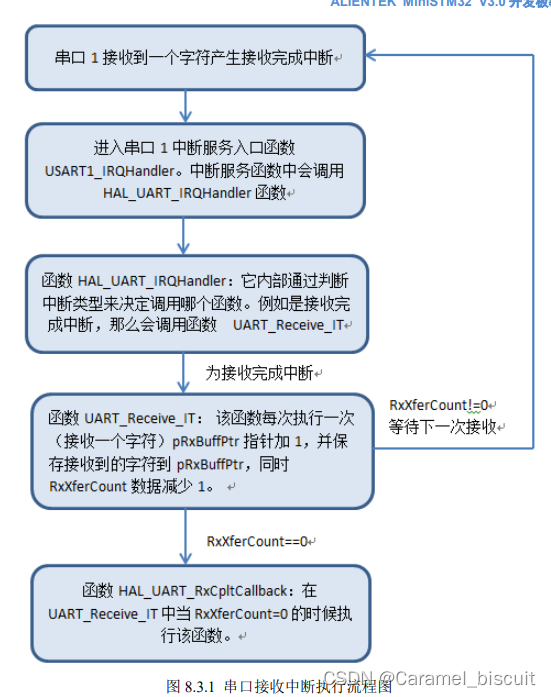
STM32 串口学习(二)
要用跳线帽将PA9与RXD相连,PA10与TXD相连。 软件设计 void uart_init(u32 baud) {//UART 初始化设置UART1_Handler.InstanceUSART1; //USART1UART1_Handler.Init.BaudRatebound; //波特率UART1_Handler.Init.WordLengthUART_WORDLENGTH_8B; //字长为 8 位数据格式U…...
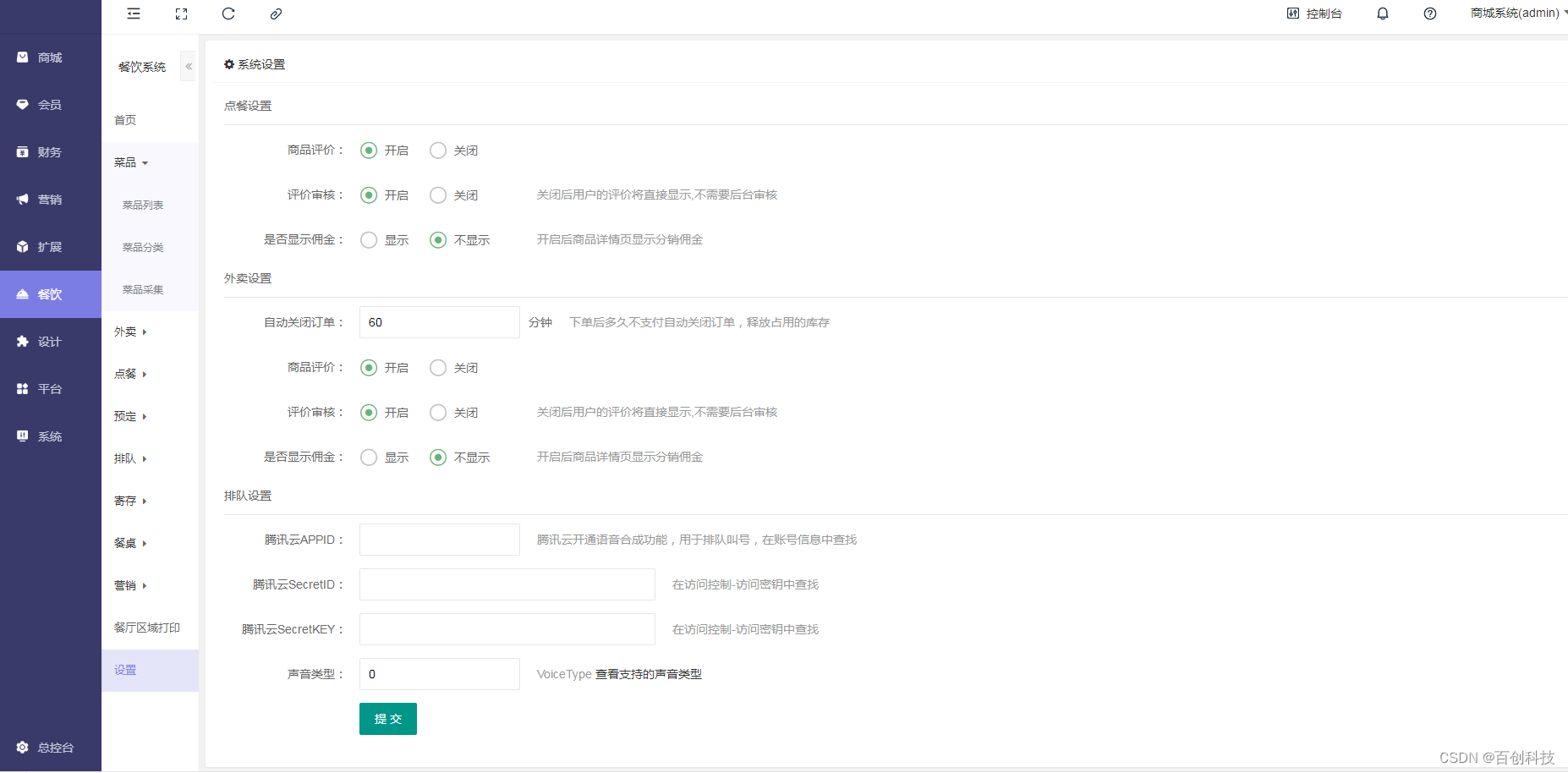
点大商城V2_2.5.0 全开源版 商家自营+多商户入驻 百度+支付宝+QQ+头条+小程序端+unipp开源前端安装测试教程
安装测试环境:Nginx 1.20PHP7.2MySQL 5.6 修复了无法上传开放平台问题 安装说明: 1、上传后端目录至网站 2、导入提供的数据库文件 3、修改数据库配置文件根目录下config.php,增加数据库用户名和密码 4、网站后台直接访问网址ÿ…...

“深入理解SpringBoot:从入门到精通“
标题:深入理解Spring Boot:从入门到精通 摘要:本文将介绍Spring Boot的基本概念和核心特性,并通过示例代码演示如何使用Spring Boot构建一个简单的Web应用程序。 1. 简介 Spring Boot是一个开源的Java框架,旨在简化基…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...

Spring Security 认证流程——补充
一、认证流程概述 Spring Security 的认证流程基于 过滤器链(Filter Chain),核心组件包括 UsernamePasswordAuthenticationFilter、AuthenticationManager、UserDetailsService 等。整个流程可分为以下步骤: 用户提交登录请求拦…...

JS红宝书笔记 - 3.3 变量
要定义变量,可以使用var操作符,后跟变量名 ES实现变量初始化,因此可以同时定义变量并设置它的值 使用var操作符定义的变量会成为包含它的函数的局部变量。 在函数内定义变量时省略var操作符,可以创建一个全局变量 如果需要定义…...
