Box-Cox 变换
Box-cox 变化公式如下:
y ( λ ) = { y λ − 1 λ λ ≠ 0 l n ( y ) λ = 0 y^{(\lambda)}=\left\{ \begin{aligned} \frac{y^{\lambda} - 1}{\lambda} && \lambda \ne 0 \\ ln(y) && \lambda = 0 \end{aligned} \right. y(λ)=⎩ ⎨ ⎧λyλ−1ln(y)λ=0λ=0
y ( λ ) = { ( y + a ) λ − 1 λ λ ≠ 0 l n ( y + a ) λ = 0 y^{(\lambda)}=\left\{ \begin{aligned} \frac{(y + a)^{\lambda} - 1}{\lambda} && \lambda \ne 0 \\ ln(y + a) && \lambda = 0 \end{aligned} \right. y(λ)=⎩ ⎨ ⎧λ(y+a)λ−1ln(y+a)λ=0λ=0
根据参数 λ \lambda λ的取值不同,box-cox变换包含了三类函数族:对数函数族、指数函数族、导致函数。
变换的目标是使得变换后因变量线性回归模型的等方差、不相关、正太等假设:
y ( λ ) = [ y 1 ( λ ) y 2 ( λ ) . . . y n ( λ ) ] ∼ N ( X β , σ 2 I ) \bold{y}^{(\lambda)} = \left[\begin{array}{c} y_1^{(\lambda)} \\ y_2^{(\lambda)} \\ ... \\ y_n^{(\lambda)} \end{array}\right]\sim\mathcal{N}(\bold{X}\bold{\beta}, \sigma^2\bold{I}) y(λ)= y1(λ)y2(λ)...yn(λ) ∼N(Xβ,σ2I)
L ( β , σ 2 ) = ( 1 2 π σ ) n e x p ( − 1 2 σ 2 ( y ( λ ) − X β ) ′ ( y ( λ ) − X β ) ) J L(\beta,\sigma^2) = (\frac{1}{\sqrt{2\pi}\sigma})^nexp(-\frac{1}{2\sigma^2}(\bold{y}^{(\lambda)} - \bold{X\beta})'(\bold{y}^{(\lambda)} - \bold{X\beta}))\bold{J} L(β,σ2)=(2πσ1)nexp(−2σ21(y(λ)−Xβ)′(y(λ)−Xβ))J
J = ∏ i = 1 n ∣ d y i ( λ ) d y i ∣ = ∏ i = 1 n y i λ − 1 \bold{J} = \prod_{i=1}^n|\frac{dy_i^{(\lambda)}}{dy_i}| = \prod_{i=1}^ny_i^{\lambda - 1} J=i=1∏n∣dyidyi(λ)∣=i=1∏nyiλ−1
当 λ \lambda λ固定, J J J是不依赖 β , σ 2 \beta,\sigma^2 β,σ2的常数。
求得 β , σ 2 \beta,\sigma^2 β,σ2的最大似然估计为:
β ^ = ( X ′ X ) − 1 X ′ y ( λ ) \hat{\beta} = (X'X)^{-1}X'y^{(\lambda)} β^=(X′X)−1X′y(λ)
σ ^ 2 = 1 n y ( λ ) ′ ( I − X ( X ′ X ) − 1 X ′ ) y ( λ ) = 1 n S S E ( λ , y ( λ ) ) , S S E ( λ , y ( λ ) ) = y ( λ ) ′ ( I − X ( X ′ X ) − 1 X ′ ) y ( λ ) \hat{\sigma}^2 = \frac{1}{n}y^{(\lambda)'}(I - X(X'X)^{-1}X')y^{(\lambda)} = \frac{1}{n}SSE(\lambda, y^{(\lambda)}), SSE(\lambda, y^{(\lambda)}) = y^{(\lambda)'}(I - X(X'X)^{-1}X')y^{(\lambda)} σ^2=n1y(λ)′(I−X(X′X)−1X′)y(λ)=n1SSE(λ,y(λ)),SSE(λ,y(λ))=y(λ)′(I−X(X′X)−1X′)y(λ)
对应的似然函数为:
L ( β ^ , σ ^ 2 ) = ( 2 π e S S E ( λ , y ( λ ) ) n ) − n 2 ∗ J L(\hat{\beta}, \hat{\sigma}^2) = (2\pi e \frac{SSE(\lambda, y^{(\lambda)})}{n})^{-\frac{n}{2}} * J L(β^,σ^2)=(2πenSSE(λ,y(λ)))−2n∗J
l n L ( β ^ , σ ^ 2 ) = − n 2 l n ( S S E ( λ , y λ ) ) + l n ( J ) = − n 2 l n ( S S E ( λ , z ( λ ) ) ) lnL(\hat{\beta},\hat{\sigma}^2) = -\frac{n}{2}ln(SSE(\lambda,y^{\lambda})) + ln(J) = -\frac{n}{2}ln(SSE(\lambda, z^{(\lambda)})) lnL(β^,σ^2)=−2nln(SSE(λ,yλ))+ln(J)=−2nln(SSE(λ,z(λ)))
z ( λ ) = y ( λ ) J z^{(\lambda)} = \frac{y^{(\lambda)}}{\bold{J}} z(λ)=Jy(λ)
为了找出 λ \lambda λ的极大似然估计,使得 S S E ( λ , z ( λ ) ) SSE(\lambda,z^{(\lambda)}) SSE(λ,z(λ))达到最小即可。
相关文章:

Box-Cox 变换
Box-cox 变化公式如下: y ( λ ) { y λ − 1 λ λ ≠ 0 l n ( y ) λ 0 y^{(\lambda)}\left\{ \begin{aligned} \frac{y^{\lambda} - 1}{\lambda} && \lambda \ne 0 \\ ln(y) && \lambda 0 \end{aligned} \right. y(λ)⎩ ⎨ ⎧λyλ−1ln…...

Linux wc命令用于统计文件的行数,字符数,字节数
Linux wc命令用于计算字数。 利用wc指令我们可以计算文件的Byte数、字数、或是列数,若不指定文件名称、或是所给予的文件名为"-",则wc指令会从标准输入设备读取数据。 语法 wc [-clw][–help][–version][文件…] 参数: -c或–b…...
Python读取多个栅格文件并提取像元的各波段时间序列数据与变化值
本文介绍基于Python语言,读取文件夹下大量栅格遥感影像文件,并基于给定的一个像元,提取该像元对应的全部遥感影像文件中,指定多个波段的数值;修改其中不在给定范围内的异常值,并计算像元数值在每一景遥感影…...

Linux 之 wget curl
wget 命令 wget是非交互式的文件下载器,可以在命令行内下载网络文件 语法: wget [-b] url 选项: -b ,可选,background 后台下载,会将日志写入到 当前工作目录的wget-log文件 参数 url : 下载链…...

AngularJS 和 React区别
目录 1. 背景:2. 版本:3. 应用场景:4. 语法:5. 优缺点:6. 代码示例: AngularJS 和 React 是两个目前最为流行的前端框架之一。它们有一些共同点,例如都是基于 JavaScript 的开源框架,…...
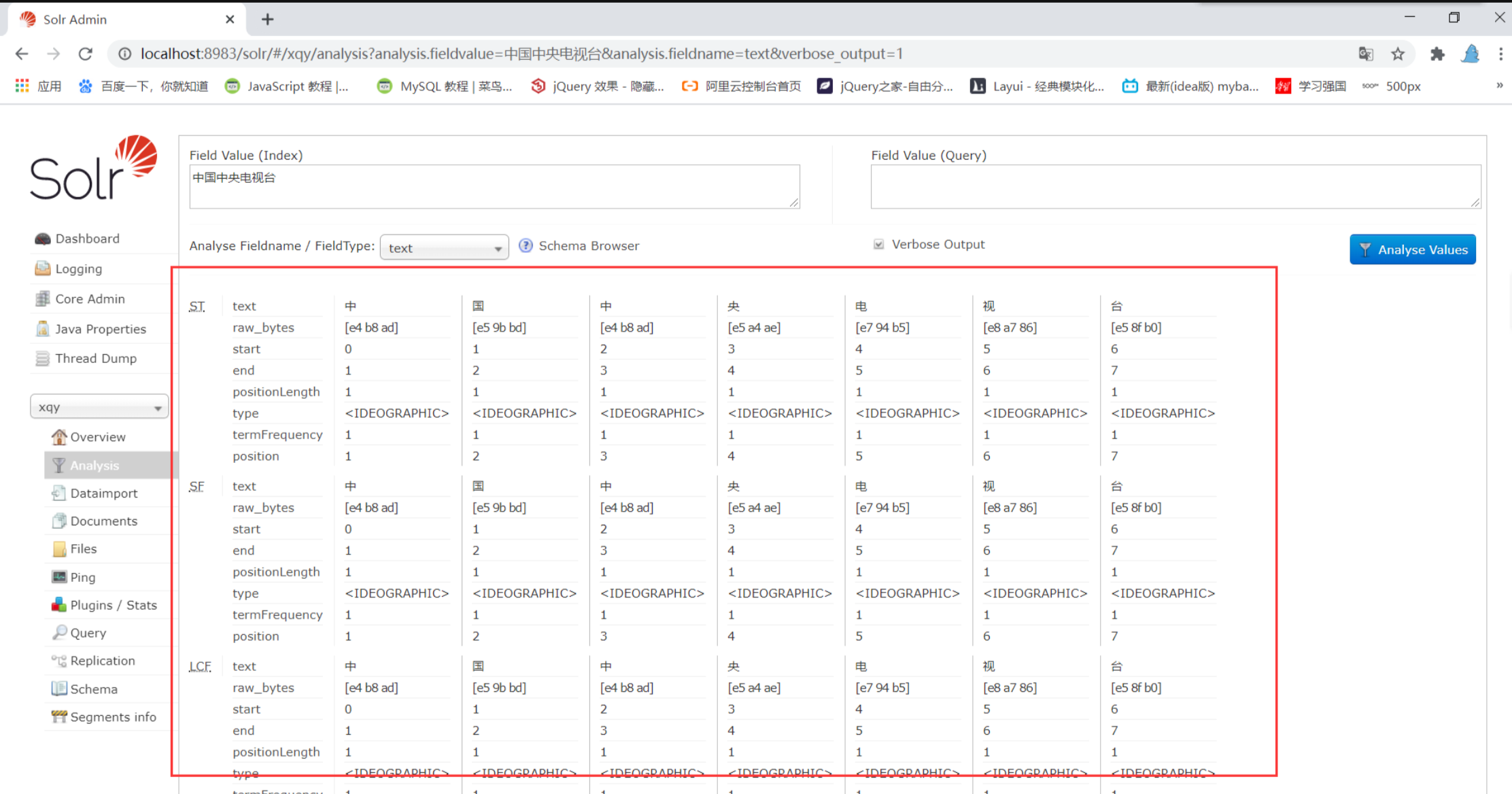
【Solr】Solr搜索引擎使用
文章目录 一、什么是Solr?二 、数据库本身就支持搜索啊,干嘛还要搞个什么solr?三、如果我们想要使用solr那么首先我们得安装它 一、什么是Solr? 其实我们大多数人都使用过Solr,也许你不会相信我说的这句话,但是事实却是如此啊 ! 每当你想买自己喜欢的东东时,你可能会打开某…...
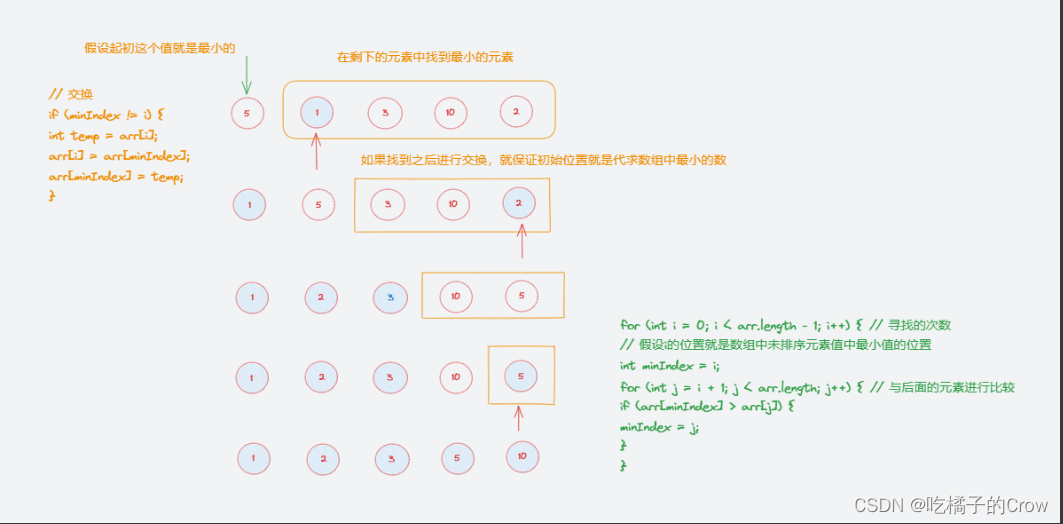
一起学算法(选择排序篇)
距离上次更新已经很久了,以前都是非常认真的写笔记进行知识分享,但是带来的情况并不是很好,一度认为发博客是没有意义的,但是这几天想了很多,已经失去了当时写博客的初心了,但是我觉得应该做点有意义的事&a…...

智能体的主观和能动
摘要 智能体的主动性是提升智能机器的能力的关键。围绕智能体的主动性存在很多思想迷雾,本文继续我们以前的工作,试图清理这些概念上的问题。我们的讨论显示:要研究主动性,并不一定需要研究意识,仅需要研究主观和能动就…...
AB 压力测试
服务器配置 阿里云Ubuntu 64位 CPU1 核 内存2 GB 公网带宽1 Mbps ab -c100 -n1000 http://127.0.0.1:9501/ -n:在测试会话中所执行的请求个数。默认时,仅执行一个请求。 -c:一次产生的请求个数。默认是一次一个。 ab -c 100 -n 200 ht…...
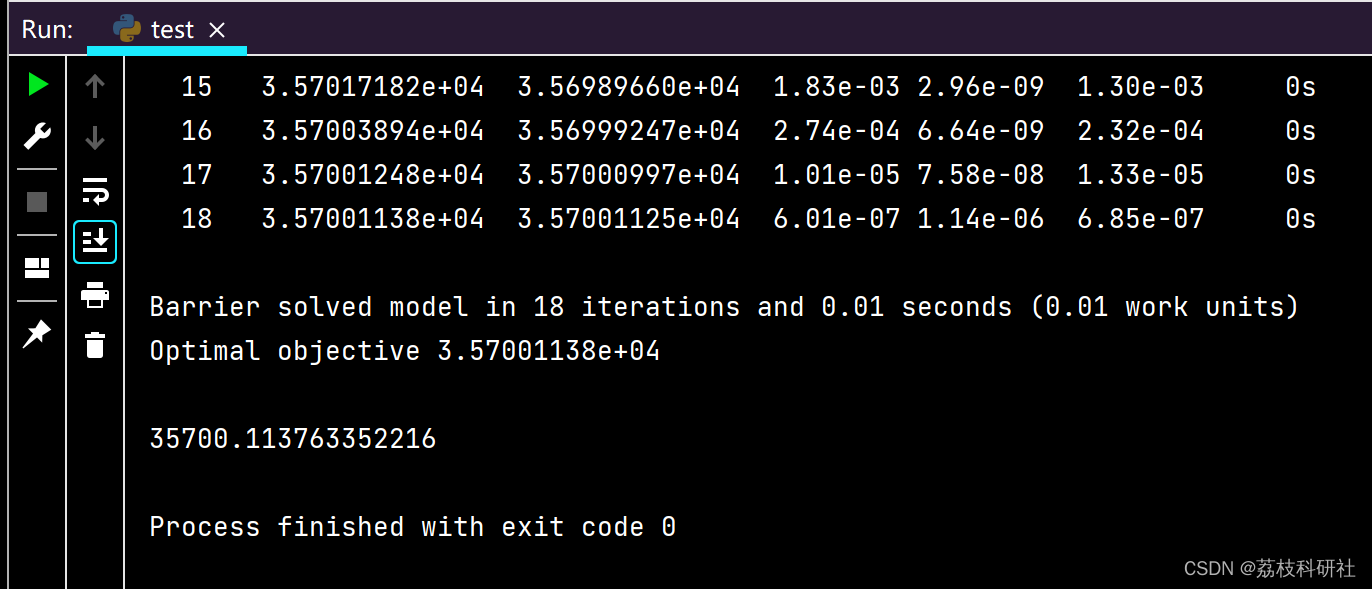
多旋翼物流无人机节能轨迹规划(Python代码实现)
目录 💥1 概述 📚2 运行结果 🌈3 Python代码实现 🎉4 参考文献 💥1 概述 多旋翼物流无人机的节能轨迹规划是一项重要的技术,可以有效减少无人机的能量消耗,延长飞行时间,提高物流效率…...

Vue通过指令 命令将打包好的dist静态文件上传到腾讯云存储桶 (保存原有存储目录结构)
1、在项目根目录创建uploadToCOS.js文件 (建议起简单的名字 方便以后上传输入命令方便) 2、uploadToCOS.js文件代码编写 const path require(path); const fs require(fs); const COS require(cos-nodejs-sdk-v5);// 配置腾讯云COS参数 const cos n…...

Linux 新硬盘分区,挂载
在Linux系统中,当你插入新的硬盘时,你需要进行一些步骤来使系统识别并使用它。以下是一些常见的步骤: 确保硬盘已正确连接到计算机。检查硬盘的电源和数据线是否牢固连接。 打开终端或命令行界面。 运行以下命令来扫描新硬盘: s…...
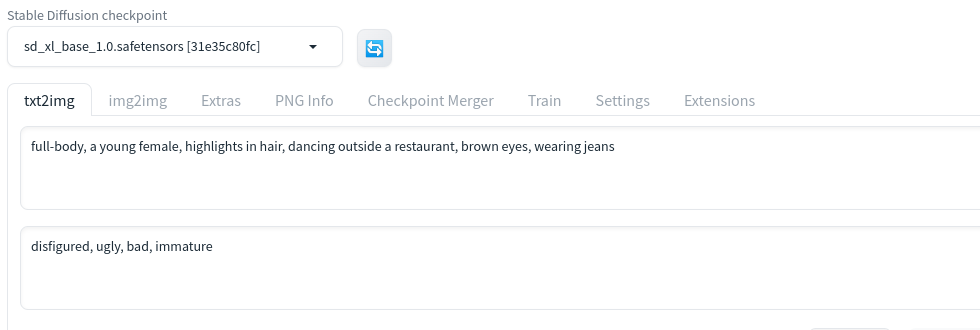
Stable Diffusion 开源模型 SDXL 1.0 发布
关于 SDXL 模型,之前写过两篇: Stable Diffusion即将发布全新版本Stable Diffusion XL 带来哪些新东西? 一晃四个月的时间过去了,Stability AI 团队终于发布了 SDXL 1.0。当然在这中间发布过几个中间版本,分别是 SDXL …...

NoSQL--------- Redis配置与优化
目录 一、关系型数据库与非关系型数据库 1.1关系型数据库 1.2非关系型数据库Nosql 1.3关系与非关系区别 1.4非关系产生的背景 1.5总结 二、Redis介绍 2.1Redis简介 2.3Redis优点 2.4 Redis为什么这么快? 三、Redis安装部署 3.1安装redis 3.2测试redis 3.3r…...

Ubuntu中关闭防火墙
在Ubuntu中关闭防火墙可以通过以下步骤进行: 查看防火墙状态: sudo ufw status如果防火墙状态为active(活动状态),则执行以下命令来停用防火墙: sudo ufw disable输入以下命令确认是否停用防火墙&#x…...

java-马踏棋盘
在8x8的国际棋盘上,按照马走日的规则,验证是否能够走遍棋盘。 1、创建棋盘 chessBoard,是一个二维数组。 2、将当前位置设置为已经访问,然后根据当前位置,计算马儿还能走哪些位置,并放入到一个集合中&…...
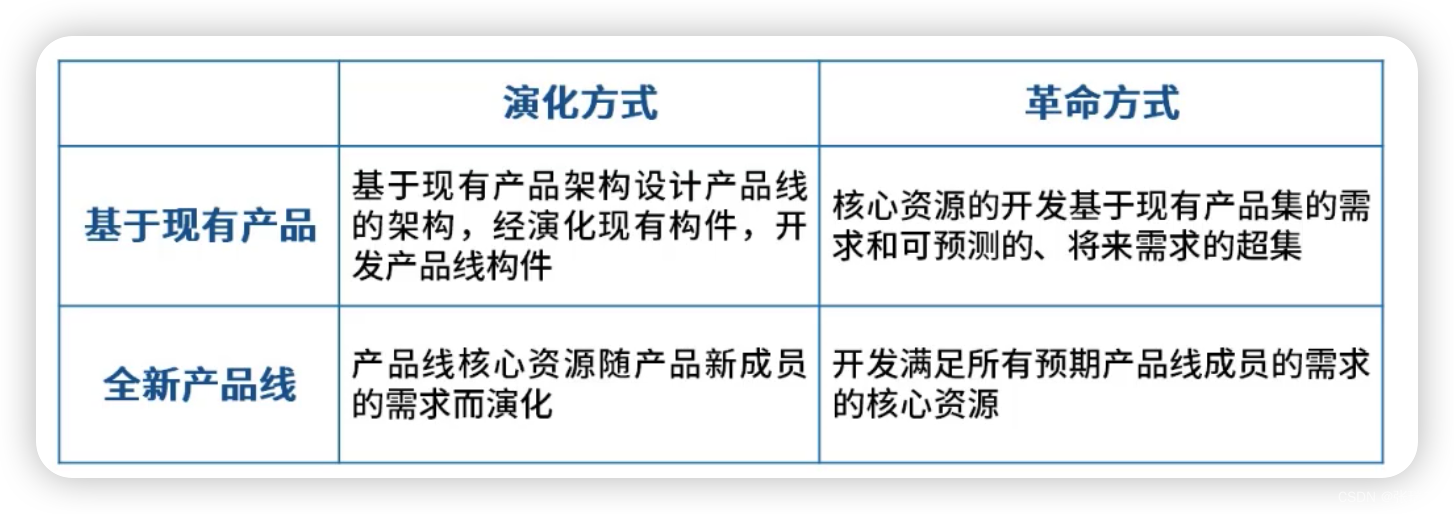
系统架构设计师-软件架构设计(4)
目录 一、软件架构评估 1、敏感点 2、权衡点 3、风险点 4、非风险点 5、架构评估方法 5.1 基于调查问卷或检查表的方式 5.2 基于度量的方式 5.3 基于场景的方式 6、基于场景的评估方法 6.1 软件架构分析法(SAAM) 6.2 架构权衡分析法(ATAM&am…...
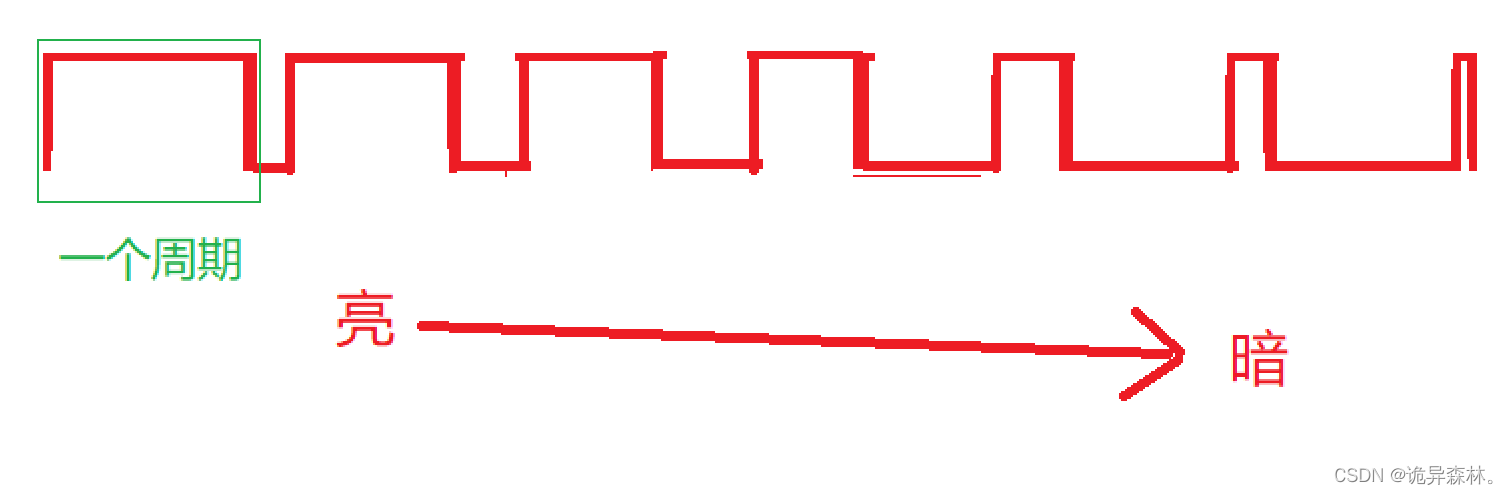
51单片机--AD/DA
AD/DA介绍 AD和DA是模拟信号和数字信号之间的转换过程。 AD,全称为模拟到数字(Analog-to-Digital),指的是将模拟信号转换为数字信号的过程。在AD转换中,模拟信号经过采样、量化和编码等步骤,被转换为离散的…...
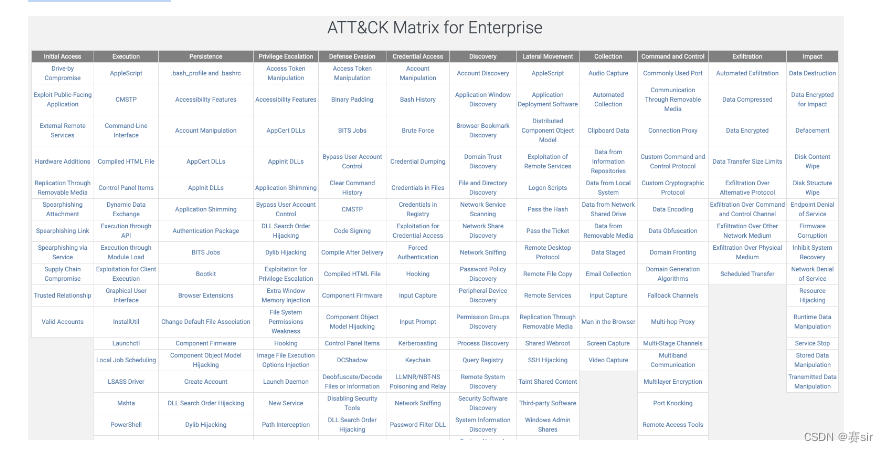
网络安全-防御需知
目录 网络安全-防御 1.网络安全常识及术语 资产 漏洞 0day 1day 后门 exploit APT 2.什么会出现网络安全问题? 网络环境的开放性 协议栈自身的脆弱性 操作系统自身的漏洞 人为原因 客观原因 硬件原因 缓冲区溢出攻击 缓冲区溢出攻击原理 其他攻击…...
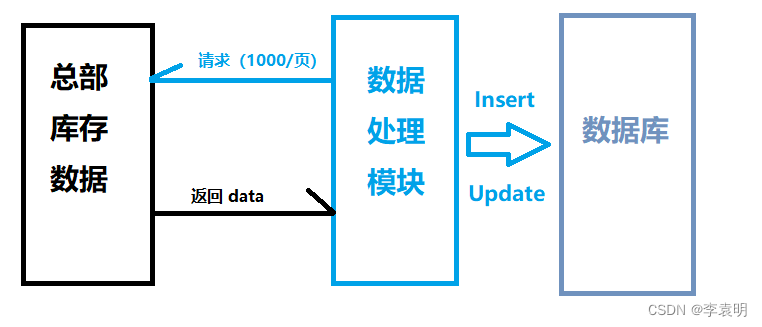
C#百万数据处理
C#百万数据处理 在我们经验的不断增长中不可避免的会遇到一些数据量很大操作也复杂的业务 这种情况我们如何取优化如何去处理呢?一般都要根据业务逻辑和背景去进行合理的改进。 文章目录 C#百万数据处理前言一、项目业务需求和开发背景项目开发背景数据量计算业务需…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

学习一下用鸿蒙DevEco Studio HarmonyOS5实现百度地图
在鸿蒙(HarmonyOS5)中集成百度地图,可以通过以下步骤和技术方案实现。结合鸿蒙的分布式能力和百度地图的API,可以构建跨设备的定位、导航和地图展示功能。 1. 鸿蒙环境准备 开发工具:下载安装 De…...
