如何理解Diffusion
Diffusion算法可以有多个角度进行理解,不同的理解方式只是对目标函数进行了不同的解释。其主体思想是不变的,可以归纳为:
- 训练时通过图片逐步添加噪声,变为一个纯噪声。然后学习每一步的噪声。
- 推理时给定一个随机噪声图片,然后通过学习到的噪声生成一个新的图片
目标
目标是已知上一步图像时,下一步图像的分布是什么。
每一步的图片用 x 0 , x 1 , . . . , x T x_0, x_1, ..., x_T x0,x1,...,xT来表示,其中 x 0 x_0 x0是原图, x T x_T xT是纯噪声。它们的关系是:
x t = α t x t − 1 + 1 − α t ϵ with ϵ ∼ N ( ϵ ; 0 , I ) \begin{align} \boldsymbol{x}_t = \sqrt{\alpha_t}\boldsymbol{x}_{t-1} + \sqrt{1 - \alpha_t}\boldsymbol{\epsilon} \quad \text{with } \boldsymbol{\epsilon} \sim \mathcal{N}(\boldsymbol{\epsilon}; \boldsymbol{0}, \textbf{I}) \end{align} xt=αtxt−1+1−αtϵwith ϵ∼N(ϵ;0,I)
其中:
- ϵ \epsilon ϵ:是噪声,用一个均值为0,方差为I的高斯分布表示
- α t \alpha_t αt:是一个常数,只和t相关
为什么使用这个式子?可以看出,后一步的图片其实是前一步图片 x t − 1 x_{t-1} xt−1和另外一个噪声 ϵ \epsilon ϵ加权求和得到的。
我们需要把 x t − 1 x_{t-1} xt−1用 x t x_t xt表示,然后一步一步就可以推到 x 0 x_0 x0了:

这时候可能会有人想:上面那个式子不是有 x t − 1 x_{t-1} xt−1和 x t x_t xt吗?直接用上面那个式子不就可以了。
事实上, x t − 1 x_{t-1} xt−1和 x t x_t xt都是随机变量,可以进行恒等变换,但是算出来的仍然是一个随机变量。我们必须知道随机变量的分布才可以。
因此我们需要知道的其实是已知 x t x_t xt时 x t − 1 x_{t-1} xt−1的分布: q ( x t − 1 ∣ x t , x 0 ) q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0) q(xt−1∣xt,x0),而这个值可以用贝叶斯公式变换为:
q ( x t − 1 ∣ x t , x 0 ) = q ( x t ∣ x t − 1 , x 0 ) q ( x t − 1 ∣ x 0 ) q ( x t ∣ x 0 ) q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0) = q(\mathbf{x}_t \vert \mathbf{x}_{t-1}, \mathbf{x}_0) \frac{ q(\mathbf{x}_{t-1} \vert \mathbf{x}_0) }{ q(\mathbf{x}_t \vert \mathbf{x}_0) } q(xt−1∣xt,x0)=q(xt∣xt−1,x0)q(xt∣x0)q(xt−1∣x0)
这个式子中的值都是已知的,因为 x t x_{t} xt和 x t − 1 x_{t-1} xt−1的递推关系是已知的,因此可以不断地带入,然后使用 x 0 x_0 x0来表示 x t x_{t} xt
具体如下:
x t = α ˉ t x 0 + 1 − α ˉ t ϵ 0 \begin{align} \boldsymbol{x}_t = \sqrt{\bar\alpha_t}\boldsymbol{x}_0 + \sqrt{1 - \bar\alpha_t}\boldsymbol{\boldsymbol{\epsilon}}_0 \\ \end{align} xt=αˉtx0+1−αˉtϵ0
其中 α t ˉ \bar{\alpha_t} αtˉ指的是累乘: α 1 ⋅ α 2 ⋅ . . . ⋅ α t \alpha_1\cdot \alpha_2\cdot ...\cdot\alpha_t α1⋅α2⋅...⋅αt
上面的式子其实就是三个高斯分布相乘除,那么通过代入高斯分布的公式,然后经过一通计算以后,可以获得 q ( x t − 1 ∣ x t , x 0 ) q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0) q(xt−1∣xt,x0),它的值如下:
q ( x t − 1 ∣ x t , x 0 ) = q ( x t ∣ x t − 1 , x 0 ) q ( x t − 1 ∣ x 0 ) q ( x t ∣ x 0 ) ∝ exp ( − 1 2 ( ( x t − α t x t − 1 ) 2 β t + ( x t − 1 − α ˉ t − 1 x 0 ) 2 1 − α ˉ t − 1 − ( x t − α ˉ t x 0 ) 2 1 − α ˉ t ) ) = exp ( − 1 2 ( x t 2 − 2 α t x t x t − 1 + α t x t − 1 2 β t + x t − 1 2 − 2 α ˉ t − 1 x 0 x t − 1 + α ˉ t − 1 x 0 2 1 − α ˉ t − 1 − ( x t − α ˉ t x 0 ) 2 1 − α ˉ t ) ) = exp ( − 1 2 ( ( α t β t + 1 1 − α ˉ t − 1 ) x t − 1 2 − ( 2 α t β t x t + 2 α ˉ t − 1 1 − α ˉ t − 1 x 0 ) x t − 1 + C ( x t , x 0 ) ) ) \begin{aligned} q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0) &= q(\mathbf{x}_t \vert \mathbf{x}_{t-1}, \mathbf{x}_0) \frac{ q(\mathbf{x}_{t-1} \vert \mathbf{x}_0) }{ q(\mathbf{x}_t \vert \mathbf{x}_0) } \\ &\propto \exp \Big(-\frac{1}{2} \big(\frac{(\mathbf{x}_t - \sqrt{\alpha_t} \mathbf{x}_{t-1})^2}{\beta_t} + \frac{(\mathbf{x}_{t-1} - \sqrt{\bar{\alpha}_{t-1}} \mathbf{x}_0)^2}{1-\bar{\alpha}_{t-1}} - \frac{(\mathbf{x}_t - \sqrt{\bar{\alpha}_t} \mathbf{x}_0)^2}{1-\bar{\alpha}_t} \big) \Big) \\ &= \exp \Big(-\frac{1}{2} \big(\frac{\mathbf{x}_t^2 - 2\sqrt{\alpha_t} \mathbf{x}_t \color{blue}{\mathbf{x}_{t-1}} \color{black}{+ \alpha_t} \color{red}{\mathbf{x}_{t-1}^2} }{\beta_t} + \frac{ \color{red}{\mathbf{x}_{t-1}^2} \color{black}{- 2 \sqrt{\bar{\alpha}_{t-1}} \mathbf{x}_0} \color{blue}{\mathbf{x}_{t-1}} \color{black}{+ \bar{\alpha}_{t-1} \mathbf{x}_0^2} }{1-\bar{\alpha}_{t-1}} - \frac{(\mathbf{x}_t - \sqrt{\bar{\alpha}_t} \mathbf{x}_0)^2}{1-\bar{\alpha}_t} \big) \Big) \\ &= \exp\Big( -\frac{1}{2} \big( \color{red}{(\frac{\alpha_t}{\beta_t} + \frac{1}{1 - \bar{\alpha}_{t-1}})} \mathbf{x}_{t-1}^2 - \color{blue}{(\frac{2\sqrt{\alpha_t}}{\beta_t} \mathbf{x}_t + \frac{2\sqrt{\bar{\alpha}_{t-1}}}{1 - \bar{\alpha}_{t-1}} \mathbf{x}_0)} \mathbf{x}_{t-1} \color{black}{ + C(\mathbf{x}_t, \mathbf{x}_0) \big) \Big)} \end{aligned} q(xt−1∣xt,x0)=q(xt∣xt−1,x0)q(xt∣x0)q(xt−1∣x0)∝exp(−21(βt(xt−αtxt−1)2+1−αˉt−1(xt−1−αˉt−1x0)2−1−αˉt(xt−αˉtx0)2))=exp(−21(βtxt2−2αtxtxt−1+αtxt−12+1−αˉt−1xt−12−2αˉt−1x0xt−1+αˉt−1x02−1−αˉt(xt−αˉtx0)2))=exp(−21((βtαt+1−αˉt−11)xt−12−(βt2αtxt+1−αˉt−12αˉt−1x0)xt−1+C(xt,x0)))
上面这个高斯分布的均值和方差可以计算如下( β t = 1 − α t \beta_t=1-\alpha_t βt=1−αt):
β ~ t = 1 − α ˉ t − 1 1 − α ˉ t ⋅ β t μ ~ t ( x t , x 0 ) = α t ( 1 − α ˉ t − 1 ) 1 − α ˉ t x t + α ˉ t − 1 β t 1 − α ˉ t x 0 \begin{aligned} \tilde{\beta}_t &= \color{green}{\frac{1 - \bar{\alpha}_{t-1}}{1 - \bar{\alpha}_t} \cdot \beta_t} \\ \tilde{\boldsymbol{\mu}}_t (\mathbf{x}_t, \mathbf{x}_0) &= \frac{\sqrt{\alpha_t}(1 - \bar{\alpha}_{t-1})}{1 - \bar{\alpha}_t} \mathbf{x}_t + \frac{\sqrt{\bar{\alpha}_{t-1}}\beta_t}{1 - \bar{\alpha}_t} \mathbf{x}_0\\ \end{aligned} β~tμ~t(xt,x0)=1−αˉt1−αˉt−1⋅βt=1−αˉtαt(1−αˉt−1)xt+1−αˉtαˉt−1βtx0
分析一下就可以知道,当 x t x_{t} xt已知时,其实这个 x t − 1 x_{t-1} xt−1的分布是已知的。有人问,那么均值中还有 x 0 x_0 x0怎么办呢,事实上可以通过上面那个递推公式的结果,使用 x t x_{t} xt把 x 0 x_0 x0表示出来,然后带入。带入后的结果如下:
μ q ( x t , x 0 ) = 1 α t x t − 1 − α t 1 − α ˉ t α t ϵ 0 β ~ t = 1 − α ˉ t − 1 1 − α ˉ t ⋅ β t \begin{align} \boldsymbol{\mu}_q(\boldsymbol{x}_t, \boldsymbol{x}_0) &= \frac{1}{\sqrt{\alpha_t}}\boldsymbol{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar\alpha_t}\sqrt{\alpha_t}}\boldsymbol{\epsilon}_0\\ \tilde{\beta}_t &= \color{green}{\frac{1 - \bar{\alpha}_{t-1}}{1 - \bar{\alpha}_t} \cdot \beta_t} \end{align} μq(xt,x0)β~t=αt1xt−1−αˉtαt1−αtϵ0=1−αˉt1−αˉt−1⋅βt
此时我们已经知道了 x t − 1 x_{t-1} xt−1的分布,只剩下一个是不知道的,就是噪声 ϵ 0 \epsilon_0 ϵ0。此时只需要用一个神经网络来估计每一步 t t t对应的 ϵ 0 \epsilon_0 ϵ0就可以了。
这也就是训练的过程:

Diffusion和VAE的关系:
VAE中引入了一个隐含的变量z,将p(x|y)看成了p(x|z)和q(z|y)这两个部分,然后获得了一个目标函数ELBO。下面的公式说明了ELBO是p(x)的下界,这个算法的目标就是最大化ELBO
log p ( x ) = log p ( x ) ∫ q ϕ ( z ∣ x ) d z = ∫ q ϕ ( z ∣ x ) log p ( x ) d z = E q ϕ ( z ∣ x ) [ log p ( x ) ] = E q ϕ ( z ∣ x ) [ log p ( x , z ) p ( z ∣ x ) ] = E q ϕ ( z ∣ x ) [ log p ( x , z ) q ϕ ( z ∣ x ) p ( z ∣ x ) q ϕ ( z ∣ x ) ] = E q ϕ ( z ∣ x ) [ log p ( x , z ) q ϕ ( z ∣ x ) ] + E q ϕ ( z ∣ x ) [ log q ϕ ( z ∣ x ) p ( z ∣ x ) ] = E q ϕ ( z ∣ x ) [ log p ( x , z ) q ϕ ( z ∣ x ) ] + D KL ( q ϕ ( z ∣ x ) ∣ ∣ p ( z ∣ x ) ) ≥ E q ϕ ( z ∣ x ) [ log p ( x , z ) q ϕ ( z ∣ x ) ] \begin{align} \log p(\boldsymbol{x}) & = \log p(\boldsymbol{x}) \int q_{\boldsymbol{\phi}}(\boldsymbol{z}\mid\boldsymbol{x})dz\\ & = \int q_{\boldsymbol{\phi}}(\boldsymbol{z}\mid\boldsymbol{x})\log p(\boldsymbol{x})dz\\ & = \mathbb{E}_{q_{\boldsymbol{\phi}}(\boldsymbol{z}\mid\boldsymbol{x})}\left[\log p(\boldsymbol{x})\right]\\ & = \mathbb{E}_{q_{\boldsymbol{\phi}}(\boldsymbol{z}\mid\boldsymbol{x})}\left[\log\frac{p(\boldsymbol{x}, \boldsymbol{z})}{p(\boldsymbol{z}\mid\boldsymbol{x})}\right]\\ & = \mathbb{E}_{q_{\boldsymbol{\phi}}(\boldsymbol{z}\mid\boldsymbol{x})}\left[\log\frac{p(\boldsymbol{x}, \boldsymbol{z})q_{\boldsymbol{\phi}}(\boldsymbol{z}\mid\boldsymbol{x})}{p(\boldsymbol{z}\mid\boldsymbol{x})q_{\boldsymbol{\phi}}(\boldsymbol{z}\mid\boldsymbol{x})}\right]\\ & = \mathbb{E}_{q_{\boldsymbol{\phi}}(\boldsymbol{z}\mid\boldsymbol{x})}\left[\log\frac{p(\boldsymbol{x}, \boldsymbol{z})}{q_{\boldsymbol{\phi}}(\boldsymbol{z}\mid\boldsymbol{x})}\right] + \mathbb{E}_{q_{\boldsymbol{\phi}}(\boldsymbol{z}\mid\boldsymbol{x})}\left[\log\frac{q_{\boldsymbol{\phi}}(\boldsymbol{z}\mid\boldsymbol{x})}{p(\boldsymbol{z}\mid\boldsymbol{x})}\right]\\ & = \mathbb{E}_{q_{\boldsymbol{\phi}}(\boldsymbol{z}\mid\boldsymbol{x})}\left[\log\frac{p(\boldsymbol{x}, \boldsymbol{z})}{q_{\boldsymbol{\phi}}(\boldsymbol{z}\mid\boldsymbol{x})}\right] + \mathcal{D}_{\text{KL}}(q_{\boldsymbol{\phi}}(\boldsymbol{z}\mid\boldsymbol{x}) \mid\mid p(\boldsymbol{z}\mid\boldsymbol{x}))\\ & \geq \mathbb{E}_{q_{\boldsymbol{\phi}}(\boldsymbol{z}\mid\boldsymbol{x})}\left[\log\frac{p(\boldsymbol{x}, \boldsymbol{z})}{q_{\boldsymbol{\phi}}(\boldsymbol{z}\mid\boldsymbol{x})}\right] \end{align} logp(x)=logp(x)∫qϕ(z∣x)dz=∫qϕ(z∣x)logp(x)dz=Eqϕ(z∣x)[logp(x)]=Eqϕ(z∣x)[logp(z∣x)p(x,z)]=Eqϕ(z∣x)[logp(z∣x)qϕ(z∣x)p(x,z)qϕ(z∣x)]=Eqϕ(z∣x)[logqϕ(z∣x)p(x,z)]+Eqϕ(z∣x)[logp(z∣x)qϕ(z∣x)]=Eqϕ(z∣x)[logqϕ(z∣x)p(x,z)]+DKL(qϕ(z∣x)∣∣p(z∣x))≥Eqϕ(z∣x)[logqϕ(z∣x)p(x,z)]
而VAE还有一个推广,就是Hierarchical VAE,表示中间的z不止一个,那么整个分布变成了p(x|z1), p(z1|z2), …, p(zt|y)。可以发现这个和扩散模型的思想是非常类似的。并且可以推导出来Hierarchical VAE的目标函数就是BLEO的形式是:
log p ( x ) ≥ E q ( x 1 : T ∣ x 0 ) [ log p ( x 0 : T ) q ( x 1 : T ∣ x 0 ) ] = [ t ] E q ( x 1 ∣ x 0 ) [ log p θ ( x 0 ∣ x 1 ) ] ⏟ reconstruction term − D KL ( q ( x T ∣ x 0 ) ∣ ∣ p ( x T ) ) ⏟ prior matching term − ∑ t = 2 T E q ( x t ∣ x 0 ) [ D KL ( q ( x t − 1 ∣ x t , x 0 ) ∣ ∣ p θ ( x t − 1 ∣ x t ) ) ] ⏟ denoising matching term \begin{align} \log p(\boldsymbol{x}) &\geq \mathbb{E}_{q(\boldsymbol{x}_{1:T}\mid\boldsymbol{x}_0)}\left[\log \frac{p(\boldsymbol{x}_{0:T})}{q(\boldsymbol{x}_{1:T}\mid\boldsymbol{x}_0)}\right]\\ &= \begin{aligned}[t] \underbrace{\mathbb{E}_{q(\boldsymbol{x}_{1}\mid\boldsymbol{x}_0)}\left[\log p_{\boldsymbol{\theta}}(\boldsymbol{x}_0\mid\boldsymbol{x}_1)\right]}_\text{reconstruction term} &- \underbrace{\mathcal{D}_{\text{KL}}(q(\boldsymbol{x}_T\mid\boldsymbol{x}_0) \mid\mid p(\boldsymbol{x}_T))}_\text{prior matching term} \\ &- \sum_{t=2}^{T} \underbrace{\mathbb{E}_{q(\boldsymbol{x}_{t}\mid\boldsymbol{x}_0)}\left[\mathcal{D}_{\text{KL}}(q(\boldsymbol{x}_{t-1}\mid\boldsymbol{x}_t, \boldsymbol{x}_0) \mid\mid p_{\boldsymbol{\theta}}(\boldsymbol{x}_{t-1}\mid\boldsymbol{x}_t))\right]}_\text{denoising matching term} \end{aligned} \end{align} logp(x)≥Eq(x1:T∣x0)[logq(x1:T∣x0)p(x0:T)]=[t]reconstruction term Eq(x1∣x0)[logpθ(x0∣x1)]−prior matching term DKL(q(xT∣x0)∣∣p(xT))−t=2∑Tdenoising matching term Eq(xt∣x0)[DKL(q(xt−1∣xt,x0)∣∣pθ(xt−1∣xt))]
然后扩散模型就选择了最后一项作为自己的目标函数。同时扩散模型假设了xt和xt-1之间的分布,然后把ELBO最后一项推呀推,推出最后需要学习一个噪声项。
总结一下VAE和Diffusion的区别:
- VAE的目标就是输入x,输出的y接近x的分布。做的方法是假设了一个中间变量z,然后问题变为计算两个条件概率:p(x|z)和p(z|y)。在传统VAE中这两个条件概率密度都是通过神经网络做的。
- Diffusion的目标和VAE挺类似的,但是没有用神经网络做,而是直接用一个线性的函数规定了z和x, y和z的关系(当然中间还有z1, z2, …)
- 对于VAE: 输入为x,输出为z的均值和方差: f ( x ) = ( σ , μ ) f(x)=(\sigma, \mu) f(x)=(σ,μ), f是一个神经网络
- 对于Diffusion: 规定了x和z的关系 z = α x + ( 1 − α ) ϵ z = \alpha x+(1-\alpha)\epsilon z=αx+(1−α)ϵ, ϵ \epsilon ϵ是一个高斯噪声,因此可以通过贝叶斯计算均值和方差。
- Diffusion的目标函数是VAE目标函数的一部分
相关文章:

如何理解Diffusion
Diffusion算法可以有多个角度进行理解,不同的理解方式只是对目标函数进行了不同的解释。其主体思想是不变的,可以归纳为: 训练时通过图片逐步添加噪声,变为一个纯噪声。然后学习每一步的噪声。推理时给定一个随机噪声图片&#x…...
-[聊天模型(Chat Models):使用少量示例和响应流式传输])
自然语言处理从入门到应用——LangChain:模型(Models)-[聊天模型(Chat Models):使用少量示例和响应流式传输]
分类目录:《自然语言处理从入门到应用》总目录 使用少量示例 本部分的内容介绍了如何在聊天模型(Chat Models)中使用少量示例。关于如何最好地进行少量示例提示尚未形成明确的共识。因此,我们尚未固定任何关于此的抽象概念&#…...

Java在线OJ项目(三)、前后端交互API模块
Java在线OJ项目(三)、前后端交互API模块 1. 客户端向服务器请求所有题目 或者 单个题目前端获取所有题目获取一个题目 后端 2. 后端读取前端提交的代码,进行编译运行,返回结果前端提交代码后端处理 1. 客户端向服务器请求所有题目…...

项目——负载均衡在线OJ
目录 项目介绍开发环境所用技术项目宏观结构编写思路1. 编写compile_server1.1 编译模块编写1.2 运行功能1.3compile_runner 编译与运行1.4 编写compile_server.cpp调用compile_run模块,形成网络服务 2. 编写基于MVC的oj_server2.1 oj_server.cpp的编写2.2 oj_model…...

idea连接远程服务器上传war包文件
idea连接远程服务器&上传war包 文章目录 idea连接远程服务器&上传war包1. 连接服务器2.上传war包 1. 连接服务器 选择Tools -> Start SSH Session 添加配置 连接成功 2.上传war包 Tools -> Deployment -> Browse Remote Host 点击右侧标签,点击&…...
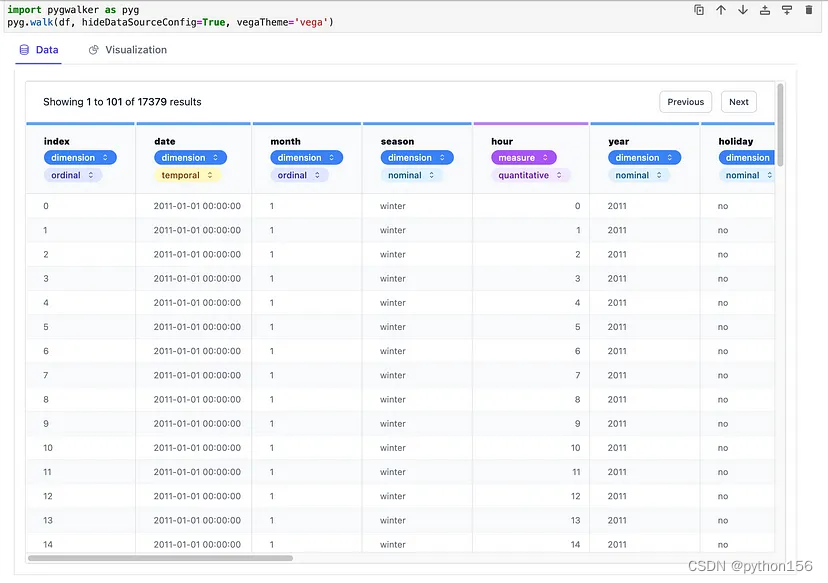
使用PyGWalker可视化分析表格型数据
大家好,可以想象一下在Jupyter Notebook中拥有大量数据,想要对其进行分析和可视化。PyGWalker就像一个神奇的工具,能让这项工作变得超级简单。它能获取用户的数据,并将其转化为一种特殊的表格,可以与之交互,…...

Visual C++中的虚函数和纯虚函数(以外观设计模式为例)
我是荔园微风,作为一名在IT界整整25年的老兵,今天来说说Visual C中的虚函数和纯虚函数。该系列帖子全部使用我本人自创的对比学习法。也就是当C学不下去的时候,就用JAVA实现同样的代码,然后再用对比的方法把C学会。 直接说虚函数…...

电子元器件选型与实战应用—01 电阻选型
大家好, 我是记得诚。 这是《电子元器件选型与实战应用》专栏的第一篇文章,今天的主角是电阻,在每一个电子产品中,都少不了电阻的身影,其重要性不言而喻。 文章目录 1. 入门知识1.1 基础1.2 常用品牌1.3 电阻的种类2. 贴片电阻标识2.1 三位数标注法2.2 四位数标注法2.3 小…...
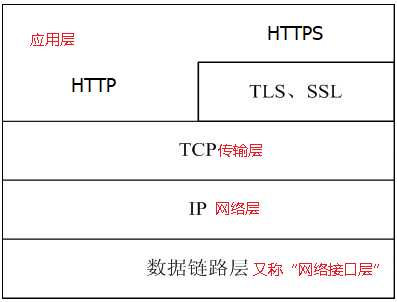
javascript 模板引擎
使用场景 在实际开发中,一般都是使用动态请求数据来更新页面,服务器端通常返回json格式的数据,正常操作是我们手动的去拼装HTML,但麻烦且容易出错,因此出现了一些用模版生成HTML的的框架叫js模板引擎如:jq…...
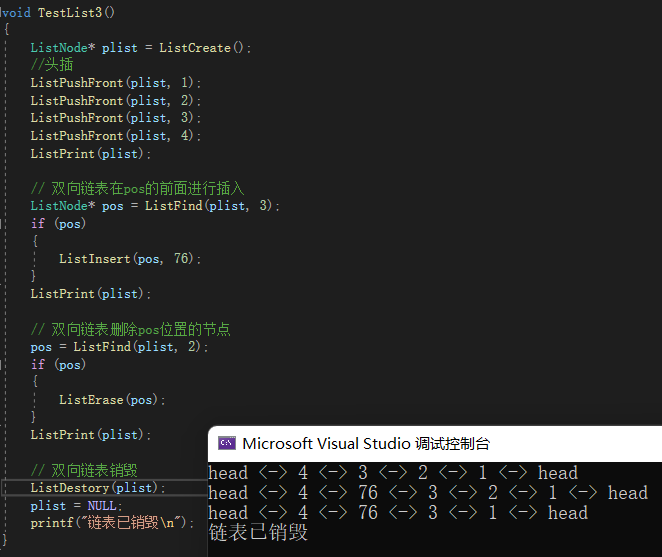
【数据结构】带头+双向+循环链表(DList)(增、删、查、改)详解
一、带头双向循环链表的定义和结构 1、定义 带头双向循环链表,有一个数据域和两个指针域。一个是前驱指针,指向其前一个节点;一个是后继指针,指向其后一个节点。 // 定义双向链表的节点 typedef struct ListNode {LTDataType dat…...
接口自动化测试平台
下载了大神的EasyTest项目demo修改了下<https://testerhome.com/topics/12648 原地址>。也有看另一位大神的HttpRunnerManager<https://github.com/HttpRunner/HttpRunnerManager 原地址>,由于水平有限,感觉有点复杂~~~ 【整整200集】超超超…...

【物联网】微信小程序接入阿里云物联网平台
微信小程序接入阿里云物联网平台 一 阿里云平台端 1.登录阿里云 阿里云物联网平台 点击进入公共实例,之前没有的点进去申请 2.点击产品,创建产品 3.产品名称自定义,按项目选择类型,节点类型选择之恋设备,联网方式W…...

PKG内容查看工具:Suspicious Package for Mac安装教程
Suspicious Package Mac版是一款Mac平台上的查看 PKG 程序包内信息的应用,Suspicious Package Mac版支持查看全部包内全部文件,比如需要运行的脚本,开发者,来源等等。 suspicious package mac使用简单,只需在选择pkg安…...

第16节:R语言医学分析实例:肺切除手术的Apriori关联规则分析
关联规则 肺切除手术的Apriori关联规则分析。 分析的目的是确定患有肺癌并需要接受肺切除术的患者的共病症状。 了解哪些症状是共病的可以帮助改善患者护理和药物处方。 分析类型是关联规则学习,通过探索变量之间的关联或频繁项集,尝试在大型数据集中找到见解和隐藏关系(H…...

ChatGPT+MidJourney 3分钟生成你的动画故事
chatgpt是真的火了,chatgpt产生了一个划时代的意义——自chatgpt起,AI是真的要落地了。 chatgpt能做的事情太多了,多到最初开发模型的程序员自己,也没法说得清楚chatgpt都能做啥,似乎只要你能想得到,它都有…...
)
在CSDN学Golang云原生(Kubernetes Pod调度)
一,NodeSelector定向调度 在 Kubernetes 中,可以使用 NodeSelector 字段来指定 Pod 调度到哪些节点上运行。NodeSelector 是一个键值对的 map,其中键是节点的标签名,值是标签值。具体步骤如下: 在节点上添加标签 首…...

Rust vs Go:常用语法对比(七)
题图来自 Go vs Rust: Which will be the top pick in programming?[1] 121. UDP listen and read Listen UDP traffic on port p and read 1024 bytes into buffer b. 听端口p上的UDP流量,并将1024字节读入缓冲区b。 import ( "fmt" "net&qu…...
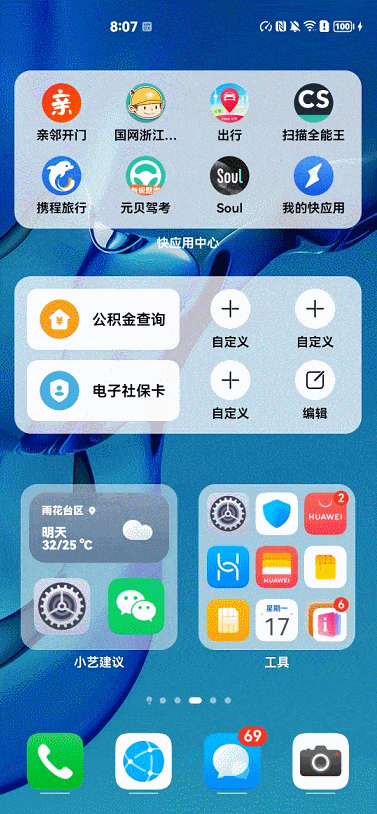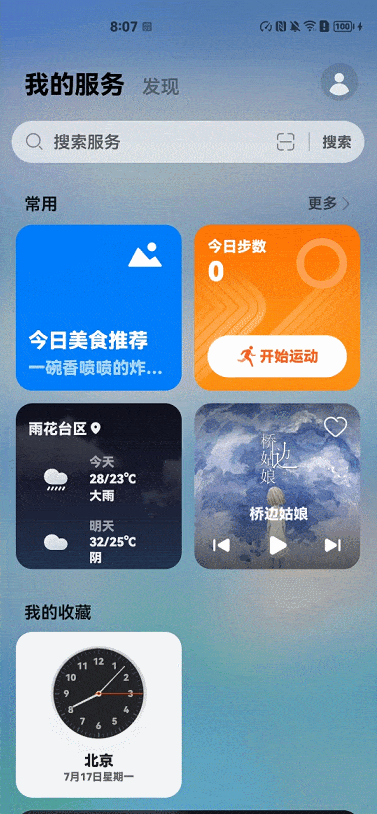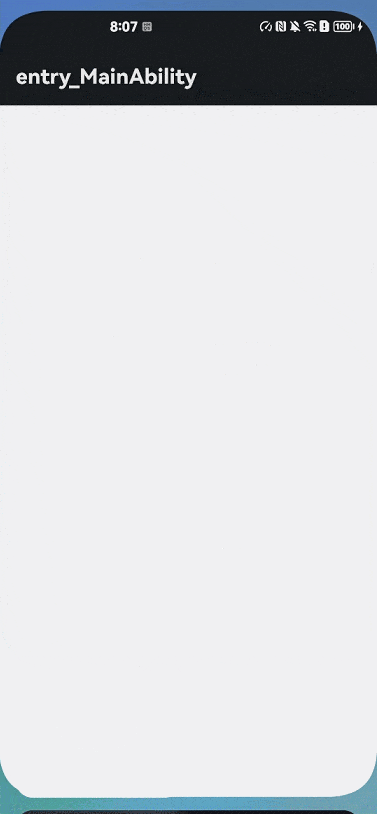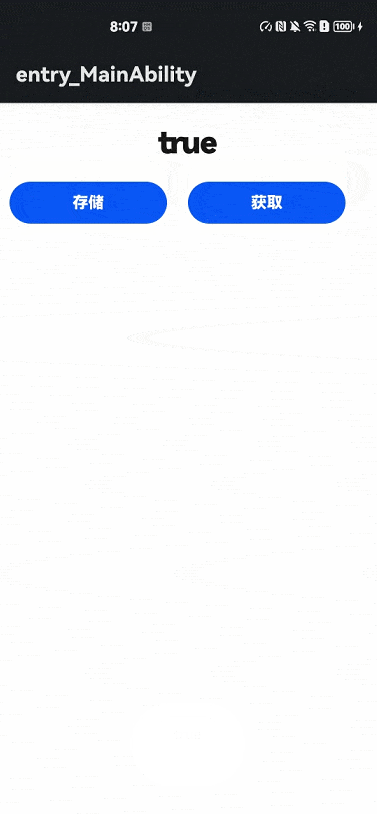
【HarmonyOS】API6使用storage实现轻量级数据存储
写在前面 本篇内容基于API6 JS语言进行开发,通过结合轻量级数据存储开发指导的文档,帮助大家完成一个实际的代码案例,通过这个小案例,可以实现简单数据的存储。 参考文档:文档中心 1、页面布局 首先我们编写一个简单…...
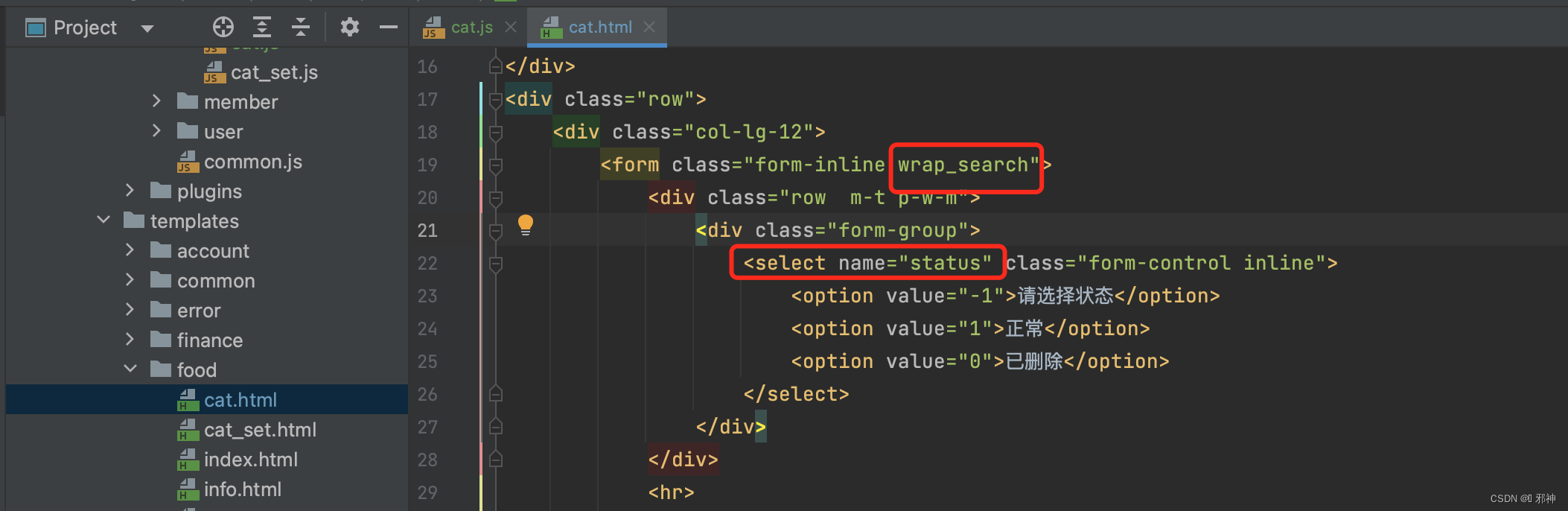
Python Flask构建微信小程序订餐系统 (十二)
🔥 创建切换商品分类状态的JS文件 🔥 ; var food_act_ops={init:function(){this.eventBind();},eventBind:function(){//表示作用域var that = this;$(".wrap_search select[name=status]").change(function(){$(".wrap_search").submit();});$(&qu…...

C++——模板的作用2:特例化
目录 模板的形式: 一.模板的多参数应用: 例: 错误使用1:使用不标准的模板形参表 编辑 错误使用2:使用变量作为实参传递给函数模板 二.模板的特例化: 类模板: 针对模板的特化步骤&am…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

【Linux】自动化构建-Make/Makefile
前言 上文我们讲到了Linux中的编译器gcc/g 【Linux】编译器gcc/g及其库的详细介绍-CSDN博客 本来我们将一个对于编译来说很重要的工具:make/makfile 1.背景 在一个工程中源文件不计其数,其按类型、功能、模块分别放在若干个目录中,mak…...

十九、【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建
【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建 前言准备工作第一部分:回顾 Django 内置的 `User` 模型第二部分:设计并创建 `Role` 和 `UserProfile` 模型第三部分:创建 Serializers第四部分:创建 ViewSets第五部分:注册 API 路由第六部分:后端初步测…...

mac:大模型系列测试
0 MAC 前几天经过学生优惠以及国补17K入手了mac studio,然后这两天亲自测试其模型行运用能力如何,是否支持微调、推理速度等能力。下面进入正文。 1 mac 与 unsloth 按照下面的进行安装以及测试,是可以跑通文章里面的代码。训练速度也是很快的。 注意…...

DBLP数据库是什么?
DBLP(Digital Bibliography & Library Project)Computer Science Bibliography是全球著名的计算机科学出版物的开放书目数据库。DBLP所收录的期刊和会议论文质量较高,数据库文献更新速度很快,很好地反映了国际计算机科学学术研…...
