数据结构---时间复杂度
专栏:数据结构
个人主页:HaiFan.
专栏简介:开学数据结构,接下来会慢慢坑新数据结构的内容!!!!
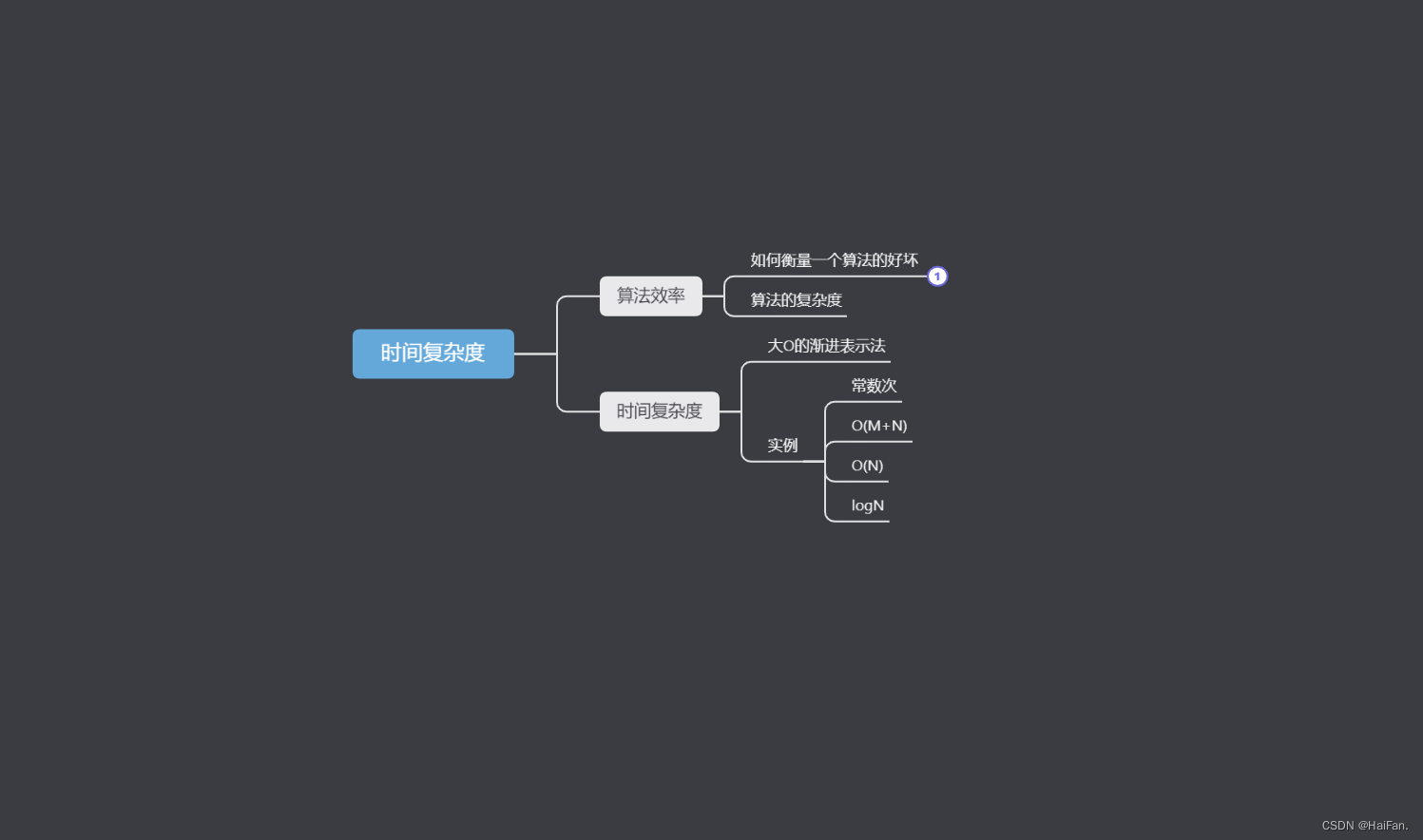
时间复杂度
- 前言
- 1.算法效率
- 1.1如何衡量一个算法的好坏
- 1.2算法的复杂度
- 2.时间复杂度
- 2.1大O的渐进表示法
- 2.2实例
- 1.常数次
- 2.O(M+N)
- 3.O(N)
- 4.logN
前言
什么是数据结构
数据结构是计算机存储,组织数据的方式,指相互之间存在一种或多种特定关系的数据与元素的集合
什么是算法
算法(Algorithm):就是定义良好的计算过程,他取一个或一组的值为输入,并产生出一个或一组值作为 输出。简单来说算法就是一系列的计算步骤,用来将输入数据转化成输出结果
1.算法效率
1.1如何衡量一个算法的好坏
比如以下的算区间和的代码
#include <iostream>
using namespace std;
const int N = 1e5 + 10;
int a[N];
int s[N];
int main()
{int n, m;cin >> n >> m;for (int i = 1; i <= n; i++){cin >> a[i];}while (m--){int l, r;cin >> l >> r;int sum = 0;for (int i = l; i <= r; i++){sum += a[i];}cout << sum << endl;}for (int i = 1; i <= n; i++){s[i] = s[i - 1] + a[i];}return 0;
}
实现这个区间和很简单,代码也很简洁,但是,简洁一定好吗?如何衡量代码的好与坏呢?
1.2算法的复杂度
举个例子:
小兰写了一个冒泡排序
小张写了一个快速排序
小兰和小张执行同一组数据,小兰花了3s,小张花了5s。
这样能说明冒泡排序的效率比快速排序的效率高吗?
答案是:不能的。
算法在编写成可执行程序后,运行时需要耗费时间资源和空间资源。因此衡量一个算法的好坏,一般是从时间和空间两个维度来衡量的,即时间复杂度和空间复杂度。
时间复杂度主要是用来衡量一个算法的运行快慢,
空间复杂度主要是用来衡量一个算法运行所需要的额外空间。
2.时间复杂度
时间复杂度:在计算机科学中,算法的时间复杂度是一个函数,他定量描述了该算法的运行时间,一个算法执行所耗费的时间,从理论上说是不能算出来的,只有把程序放在机器上跑起来,才知道,但是每个代码都需要进行一次测试吗?虽然可以,但会很麻烦,所以就有了时间复杂度这个分析方式,一个算法所花费的时间与其中语句的执行次数成正比例,算法中的基本操作的执行次数,为算法的时间复杂度。
即:找到某条基本语句与问题规模N之间的数学表达式,就是算出了该算法的时间复杂度
#include <iostream>using namespace std;int main()
{int n;cin >> n;int ret = 0;for (int i = 1; i <= n; i++){for (int j = 1; j <= n; j++){ret++;}}for (int i = 1; i <= n; i++){ret++;}int m = 100;while (m--){ret++;}cout << ret;return 0;
}
那么,这个代码中的ret共执行了多少次呢?
在代码开始,有一个双重循环,这个时候,ret++就执行了n*n次,后面又有一个循环,这个时候ret++执行了n次,最后又执行了m次ret++;
我们可以推出ret的次数:
F(n) = n*n + n + m
m是一个常数,表达式可以写成
F(n) = n * n + n + 100
- n = 10 F(n) = 100+10+100=210
- n = 100 F(n) = 100*100+100+100=1200
依次类推,当n特别大的时候,得到的函数值也是特别大的。
实际中,我们计算时间复杂度时,其实不一定要算执行次数,只需要计算大概执行次数,这就需要使用大O的渐进表示法
2.1大O的渐进表示法
大O符号(Big O notation):是用于描述函数渐进行为的数学符号。
推导大O阶方法
- 用1来取代运行时间中的所有加法常数
- 在修改后的运行次数函数中,只保留最高阶项。
- 如果最高阶项存在且不是1,则去除与这个项目相乘的常数,得到的结果就是大O阶
使用大O阶表示上面代码的时间复杂度:
O(N^2)
大O的渐进表示法去掉了那些对结果影响不大的项。
有些算法的时间复杂度存在最好,平均和最坏情况
最坏情况:任意输入规模的最大运行次数(上界)
平均情况:任意输入规模的期望运行次数
最好情况:任意输入规模的最小运行次数(下界) 例如:在一个长度为N数组中搜索一个数据x
最好情况:1次找到
最坏情况:N次找到
平均情况:N/2次找到
在实际中一般情况关注的是算法的最坏运行情况,所以数组中搜索数据时间复杂度为O(N)
2.2实例
1.常数次
#include <iostream>using namespace std;int main()
{int cnt = 0;for (int i = 1; i <= 100; i++){cnt++;}cout << cnt;return 0;
}
这个代码非常的简单,时间复杂度也很好求,因为就一个循环,并且是常数次,所以时间复杂度就是O(1)
O(1)不是代表一次,而是常数次
2.O(M+N)
#include <iostream>using namespace std;int main()
{int N;int M;cin >> N >> M;for (int i = 0; i < N; i++){;}for (int i = 0; i < M; i++){;}return 0;
}
这个代码是两个循环,第一个循环次数是N次,第二个循环次数是M次,那么时间复杂度就是O(M+N)。
值得注意的是,如果M和N相等,那么时间复杂度就是O(N)
如果不相等,就要写成O(N+M)
3.O(N)
#include <iostream>using namespace std;int main()
{int N;cin >> N;int cnt = 0;for (int i = 0; i <= N * 2; i++){cnt++;}cout << cnt;return 0;
}
循环次数是N*2,时间复杂度就是O(N)把N前面的2给省略。
4.logN
二分查找又叫折半查找,
int l = 0;
int r = n - 1;
int mid = l + r >> 1;while (l < r)
{mid = l + r >> 1;if (a[mid] >= x){r = mid;}else{l = mid + 1;}
}
二分时间复杂度最好的情况就是第一次就找到了:O(1)
最坏情况:O(logN)(以2为底)
在以2为底的对数中,一般可以写成logN,其他的不能省略
二分的最坏情况时间复杂度为什么是logN呢?
因为每次查找都会缩小区间,查找几次,就除多少个2
N/2/2/2…/2=1
2^x=N
x=logN
相关文章:

数据结构---时间复杂度
专栏:数据结构 个人主页:HaiFan. 专栏简介:开学数据结构,接下来会慢慢坑新数据结构的内容!!!! 时间复杂度前言1.算法效率1.1如何衡量一个算法的好坏1.2算法的复杂度2.时间复杂度2.1大…...

如何保证集合是线程安全的 ConcurrentHashMap如何实现高效地线程安全?
第10讲 | 如何保证集合是线程安全的? ConcurrentHashMap如何实现高效地线程安全? 我在之前两讲介绍了 Java 集合框架的典型容器类,它们绝大部分都不是线程安全的,仅有的线程安全实现,比如 Vector、Stack,在性能方面也…...

C++对象模型和this指针
成员变量和成员函数分开存储:基本概念:在C中,类内的成员变量和成员函数分开存储只有非静态成员变量才属于类的对象上每个空对象都会有一个独一无二的内存地址,所以,空对象占用内存空间的大小为1代码实现:#i…...
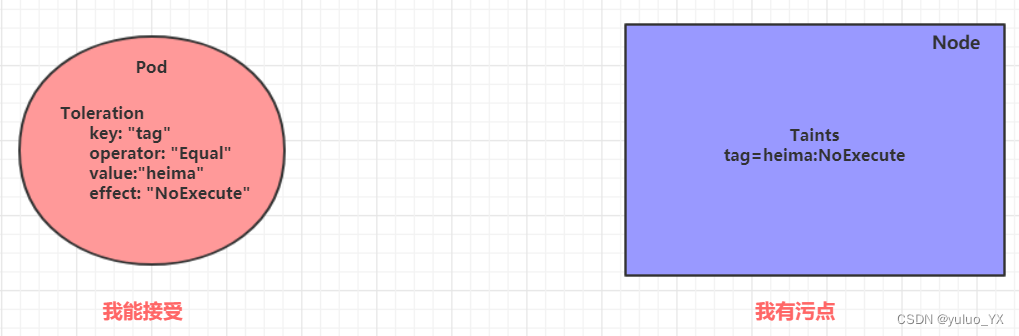
kubernetes教程 --Pod调度
Pod调度 在默认情况下,一个Pod在哪个Node节点上运行,是由Scheduler组件采用相应的算法计算出来的,这个过程是不受人工控制的。但是在实际使用中,这并不满足的需求,因为很多情况下,我们想控制某些Pod到达某…...

功率放大器科普知识(晶体管功率放大器的注意事项)
虽然功率放大器是电子实验室的常用仪器,但是很多人对于它却没有清晰的认识,下面就让安泰电子来为大家介绍功率放大器的科普内容以及使用注意事项,希望大家可以对功率放大器有清晰的认识。功率放大器可以把输入信号的功率放大,以满…...
CentOS 7转化系统为阿里龙蜥Anolis OS 7
转载:原社区CentOS 7迁移Anolis OS 7迁移手册 一、注意事项 Anolis OS 7生态上和依赖管理上保持跟CentOS7.x兼容,一键式迁移脚本centos2anolis.py,实现CentOS7.x到Anolis OS 7的平滑迁移。 使用迁移脚本前需要注意如下事项: 迁…...
【快速复习】一文看懂 Mysql 核心存储 隔离级别 锁 MVCC 机制
一文看懂 Mysql 核心存储 & 隔离级别 & 锁 & MVCC 机制 Mysql InnoDB 引擎下核心存储 数据&索引存储 IBD 文件 mysql 实际存储采用 B 树结构。 B 树是一种多路搜索树,其搜索性能高于 B 树 所有叶节点在同一深度,保证搜索效率仅叶节…...
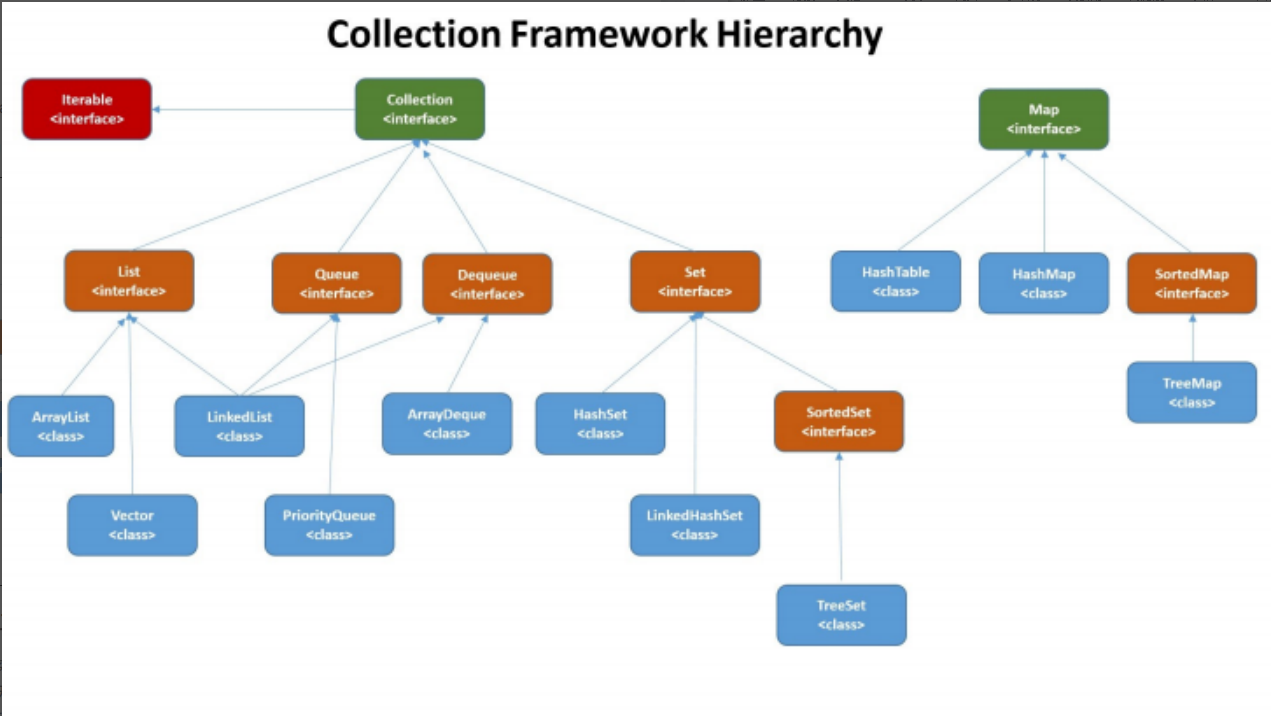
面试题----集合
概述 从上图可以看出,在Java 中除了以 Map 结尾的类之外, 其他类都实现了 Collection 接⼝。 并且,以 Map 结尾的类都实现了 Map 接⼝List,Set,Map List (对付顺序的好帮⼿): 存储的元素是有序的、可重复的。 Set (注重独⼀⽆⼆…...
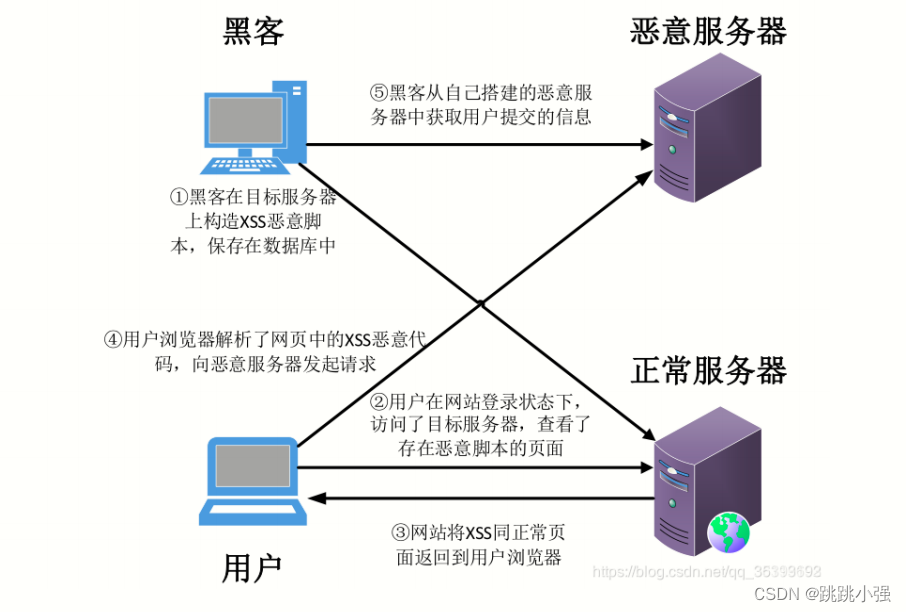
XSS注入基础入门篇
XSS注入基础入门篇1.XSS基础概念2. XSS的分类以及示例2.1 反射型XSS2.1.1 示例1:dvwa low 级别的反射型XSS2.1.2 攻击流程2.2 DOM型XSS2.2.1 示例2:DOM型XSS注入1.环境部署2.基础版本3.进阶绕过2.3 存储型XSS2.3.1 示例1:dvwa low示例2.3.2 攻…...
链表)
刷题 - 数据结构(二)链表
1. 链表 1.1 题目:合并两个有序链表 链表的建立与插入:关键在于留出头部,创建迭代指针。 ListNode* head new ListNode; // 通过new 创建了一个数据类型为ListNode的数据 并把该数据的地址赋值给ListNodeListNode* p 0; // 再创建一个数据…...

用于隔离PWM的光耦合器选择和使用
光耦合器(或光隔离器)是一种将电路电隔离的器件,不仅在隔离方面非常出色,而且允许您连接到具有不同接地层或在不同电压电平下工作的电路。光耦合器具有“故障安全”功能,因为如果受到高于最大额定值的电压,…...
面试完阿里,字节,腾讯的测试岗,复盘以及面试总结
前段时间由于某些原因辞职了,最近一直在面试。面试这段时间,经历过不同业务类型的公司(电商、酒店出行、金融、新能源、银行),也遇到了很多不同类型的面试官。 参加完三家大厂的面试聊聊我对面试的一些看法࿰…...

分享一个外贸客户案例
春节期间一个外贸人收到了客户的回复,但因为自己的处理方式造成了一个又一个问题,我们可以从中学到一些技巧和知识。“上次意大利的客人询价后,一直没回复(中间有打过电话,对方说口语不行,我写过邮件跟进过…...
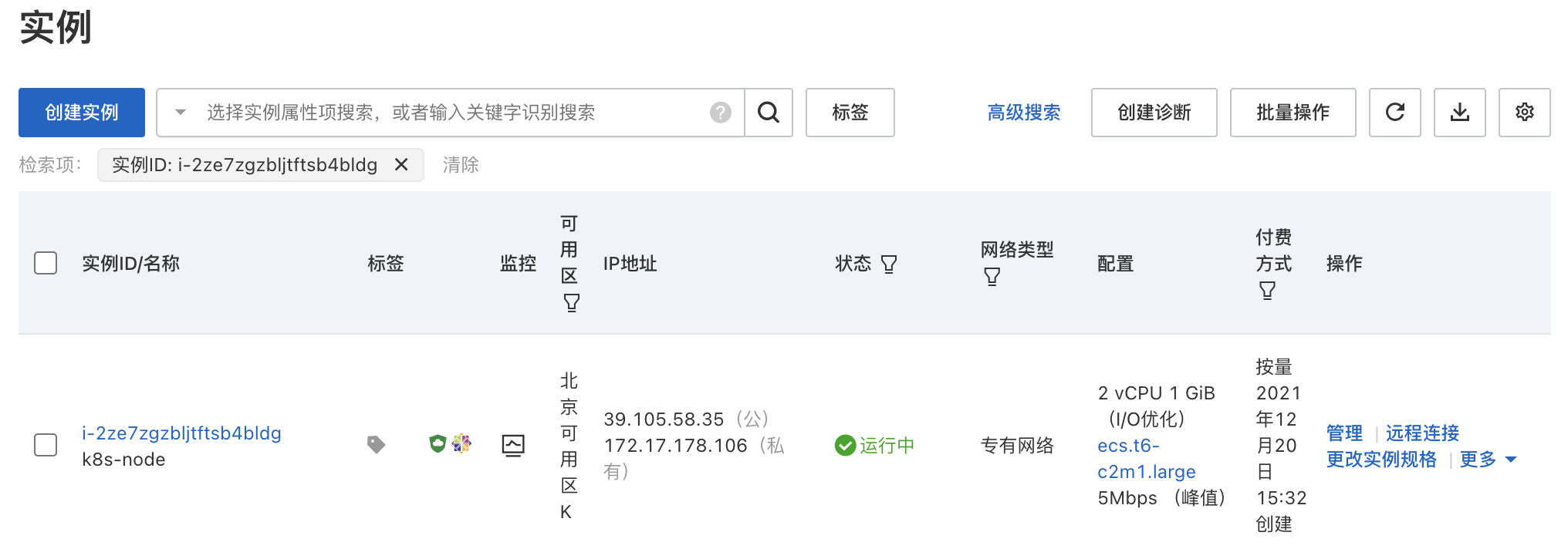
【Kubernetes】第二篇 - 购买阿里云 ECS 实例
一,前言 上一篇,简单介绍了 CI/CD 的概念以及 ECS 服务规划,搭建整套服务需要三台服务器,配置如下: ECS 配置启动服务说明2核4GJenkins Nexus Dockerci-server2核4GDocker Kubernetesk8s-master1核1GDocker Kube…...

数影周报:据传国内45亿条快递数据泄露,聆心智能完成Pre-A轮融资
本周看点:据传国内45亿条快递数据泄露;消息称微软解雇150 名云服务销售;消息称TikTok计划在欧洲再开两个数据中心;衣服长时间放购物车被淘宝客服嘲讽;聆心智能完成Pre-A轮融资......数据安全那些事据传国内45亿条快递数…...
Leetcode力扣秋招刷题路-0073
从0开始的秋招刷题路,记录下所刷每道题的题解,帮助自己回顾总结 73. 矩阵置零 给定一个 m x n 的矩阵,如果一个元素为 0 ,则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。 示例 1: 输入:mat…...

遥感数字图像处理
遥感数字图像处理 来源:慕课北京师范大学朱文泉老师的课程 遥感应用:遥感制图、信息提取 短期内了解知识结构–>有选择的剖析经典算法原理–>系统化知识结构、并尝试实践应用 跳出算法(尤其是数学公式) 关注原理及解决问…...
深度学习常用的python函数(一)
由于我只简单的学过python和pytorch,其中有很多函数的操作都还是一知半解的,其中有些函数经常见到,所以就打算记录下来。 1.zip zip(*a):针对单个可迭代对象压缩成n个元组,元组数量n等于min(a中元素的最小长度) a [(1, 2), (3…...
2023年美国大学生数学建模A题:受干旱影响的植物群落建模详解+模型代码(一)
目录 前言 一、题目理解 背景 解析: 要求 二、建模 1.相关性分析 2.相关特征权重 只希望各位以后遇到建模比赛可以艾特认识一下我,我可以提供免费的思路和部分源码,以后的数模比赛只要我还有时间肯定会第一时间写出免费开源思路&…...
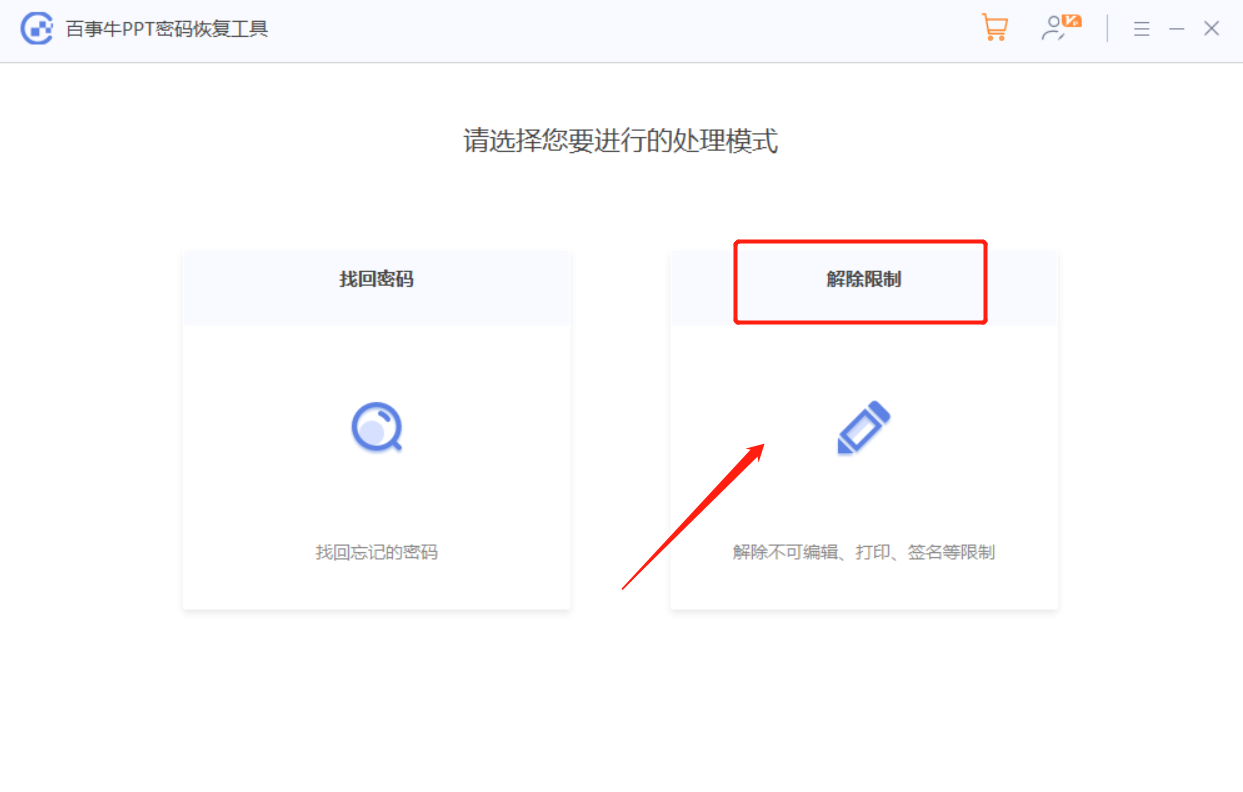
PPS文件如何转换成PPT?附两种方法
在工作中,PPS文件的使用还是很广泛的,因为作为幻灯片放映文件,点击后就能直接播放,十分方便。但如果想要修改PPS里的内容,PPS是无法编辑的,我们需要把文件转换成PPT,再进行修改。 那PPS文件如何…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...

windows系统MySQL安装文档
概览:本文讨论了MySQL的安装、使用过程中涉及的解压、配置、初始化、注册服务、启动、修改密码、登录、退出以及卸载等相关内容,为学习者提供全面的操作指导。关键要点包括: 解压 :下载完成后解压压缩包,得到MySQL 8.…...

STM32标准库-ADC数模转换器
文章目录 一、ADC1.1简介1. 2逐次逼近型ADC1.3ADC框图1.4ADC基本结构1.4.1 信号 “上车点”:输入模块(GPIO、温度、V_REFINT)1.4.2 信号 “调度站”:多路开关1.4.3 信号 “加工厂”:ADC 转换器(规则组 注入…...
