Python版本的常见模板(二) 数论(一)
文章目录
- 前言
- 质数相关
- 质数判断
- 求约数
- 求取区间质数
- 埃氏筛法
- 线性筛法
- 分解质因数
- 欧拉
- 欧拉函数
- 求取单个数
- 线性筛法求取
- 欧拉定理
- 求逆元
- 快速幂/幂取模
- 欧几里得算法
- 求最小公约数
- 拓展欧几里得算法
- 求解同余方程
前言
本文主要是提供Python版本的常见的一些与数论相关的模板,例如求解质数,质因数分解,简单博弈论,以及组合型问题(经典的括号匹配组合问题)等等。至于原理与证明的话,由于存在大量的数学公式推理,因此本文不展示,仅展示代码与变量说明和使用场景。
注意: 相关原理将使用红色字体进行标注,证明可自行查阅资料。本文不再赘述!
质数相关
质数判断
朴素方式:
def isPrim(n):if(n==1):return Falsefor i in range(2,n):if(n%i==0);return Falsereturn True
之后的话,由于除法的一些性质,当 n/d = d 的时候,d^2 = n 在这个循环过程当中 d^2 <= n 这个时候的话,是没有必要全部除去的,只需要一般就好了。
优化版本:
def isPrime(n):if(n==1):return i = 2while(i<=(n//i)):if(n%i==0):return Falsereturn True
求约数
这个的话就是前面说的那句话的比较好的运用
def yueShu(n):i = 1while(i<=n//i):if(n%i==0):print(i)if(i!=n//i):print(n//i)i+=1
此外:

求取区间质数
现在我们知道了如何判断一个质数,那么现在我们需要求取一个区间内的质数,例如,我们需要求取,从1~n之间所有的质数有哪些?
埃氏筛法
直接看到代码:
def getPrims(n):prime = [0] * (n+1):st = [False] * (n+1)cnt = 0for i in range(2,n+1):if(not st[i]):prime[cnt] = icnt+=1j = i+iwhile(j<=n):st[j] = Truej+=i这个的话,就是把这个质数的倍数给筛掉。
线性筛法
埃氏筛法的效率还是可以的,但是还可以优化一下。
def getPrim(n):prime = [0] * (n+1):st = [False] * (n+1)cnt = 0for i in range(2,n+1):if(not st[i]):prime[cnt] = icnt+=1j = 0while(prime[j] <=n//i):st[prime[j]*i] = Trueif(i%(prime[j])==0):breakj+=1
这个的话就是把那个筛选的给优化了一下。
分解质因数
ok,接下来是分解质因数,这个分解质因数是很有用的东西。
N = p1^a1 * p2*a2 …pk^ak
对于一个数N都可以拆解为这样的样子,其中这个P是质数
def division(n):i = 2while(i<=n/i):if(n%i==0):a = 0while(n%i==0):n//=ia+=1print("当前质因数为:{},对于的幂是{}".format(i,a))if(n>1):print("当前质因数为:{},对于的幂是{}".format(n,1))
欧拉
这个东西的话和我们的这个质数还是有点关系的。
欧拉函数
欧拉函数φ(5) 表示从1~5 当中和5 互质的元素个数有几个。
求取单个数
同样的和我们刚刚的这个质数是类似的,可以直接求取这个欧拉函数,也有求取一个区间的所有欧拉函数值。

def OuLa(n):res = ni = 2while(i<=(n//i)):if(n%i==0):while(n%i==0):n//=i#res = res* (1-(1/i)) 优化一下避免处于小数res = res // i *(i - 1)return res
线性筛法求取
这个的话就是求取这个1~n这个范围的所有的欧拉数
def ouLaLiner(n):prim = [0] * (n+1)st = [False] * (n+1)cnt = 0phi = [1] * (n+1) # φ(1) = 1for i in range(2,n+1):if(not st[i]):prim[cnt] = ii+=1phi[i] = phi[i-1]j = 0while(prim[j]<=n//i):st[prim[j]*i] = Trueif(i%prim[j]==0):phi[prim[j]*i] = phi[i] *(prim[j])breakphi[prim[j]*i] = phi[i] *(prim[j]-1)j+=1 欧拉定理
那么接下来就是这个欧拉定理,这个欧拉定理的话,可以用在我们的求逆元的时候用上。
这个定理非常简单。

求逆元

那么这里的话,求解的时候的话,还需要一个求快速幂的算法
快速幂/幂取模
def KuaiSu(a,k):res = 1while(k):if(k%2==0):res*=aa*=ak//=2return res
def KuaiSu(a,k,p):res = 1while(k):if(k%2==0):res*=a % pa*=a % pk//=2return res
原理是这个:
(a + b) % p = (a % p + b % p) % p(1)
(a - b) % p = (a % p - b % p ) % p (2)
(a * b) % p = (a % p * b % p) % p .(3)
欧几里得算法
求最小公约数
这里的话主要是这个欧几里得算法,这个欧几里得算法的话作用还是非常大的,一个是求取最小公约数,然后的话就是用拓展欧几里得算法来求取这个同余方程(当然这块是先用裴蜀定理可以证明一下)
def gcd(a,b):if(b==0):return areturn (b,a%b)
拓展欧几里得算法

我们使用这个拓展欧几里得算法的话可以求出这个来。
我们先来直接看到代码:
globe x=0,y=0
def exgcd(a,b,x,y):if(b == 0):x = 1,y = 0return ad = exgcd(b, a % b, y, x);y -= (a//b) * x;return d
这里的话这个y 是这样的:

求解同余方程
那么这个拓展欧几里得算法的话就可以去求解同余方程以及我们刚刚的求逆元。
因为我们那个求逆元其实也就是解一个同余方程,只是那个方程比较特殊而已。
为什么可以怎么来的如下:

这里的话就不给代码了,上面有。然后求逆的话是这样的:

相关文章:

Python版本的常见模板(二) 数论(一)
文章目录前言质数相关质数判断求约数求取区间质数埃氏筛法线性筛法分解质因数欧拉欧拉函数求取单个数线性筛法求取欧拉定理求逆元快速幂/幂取模欧几里得算法求最小公约数拓展欧几里得算法求解同余方程前言 本文主要是提供Python版本的常见的一些与数论相关的模板,例…...
)
SQL快速上手(知识点总结+训练资料)
文章目录一 SQL训练资料二 SQL知识点总结1.SQL语句的执行顺序2.窗口函数3.字符串处理函数模糊查询三 SQL题目的总结一 SQL训练资料 牛客SQL题目 猴子数据分析题目 关注的公众号 猴子数据分析 二 SQL知识点总结 1.SQL语句的执行顺序 每一个子句产生的中间结果供接下来的子句…...

无需经验的steam搬砖,每天操作1小时,轻松创业赚钱!
我作为一个95后社畜,就喜欢倒腾各种赚钱的事情,8年老韭菜告诉你,副业创收一点都不难,难就难在是否找对项目,俗话说方向不对,努力白费! 什么做苦力、技能、直播卖货,电商等等对比我这…...
如何创建你的公司的FAQ页面?
很多企业考虑为公司搭建一个“常见问题”页面,作为帮助客户回答关于产品和服务的常见问题的一种方式。 FAQ页面和登录/销售页面不同,没有展现出直接的投资回报,但是为团队节省了其他成本,据了解,高达67%的客户相比于跟…...
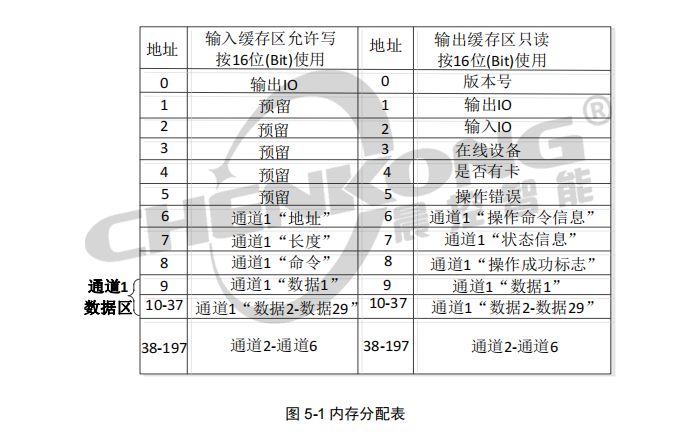
CK-GW06-E03与欧姆龙PLC配置指南
CK-GW06-E03与欧姆龙PLC配置指南CK-GW06-E03是一款支持标准工业EtherCAT协议的网关控制器,方便用户集成到PLC等控制系统中。本控制器提供了网络 POE 供电和直流电源供电两种方式,确保用户在使用无POE供电功能的交换机时可采用外接电源供电;系统还集成了六…...
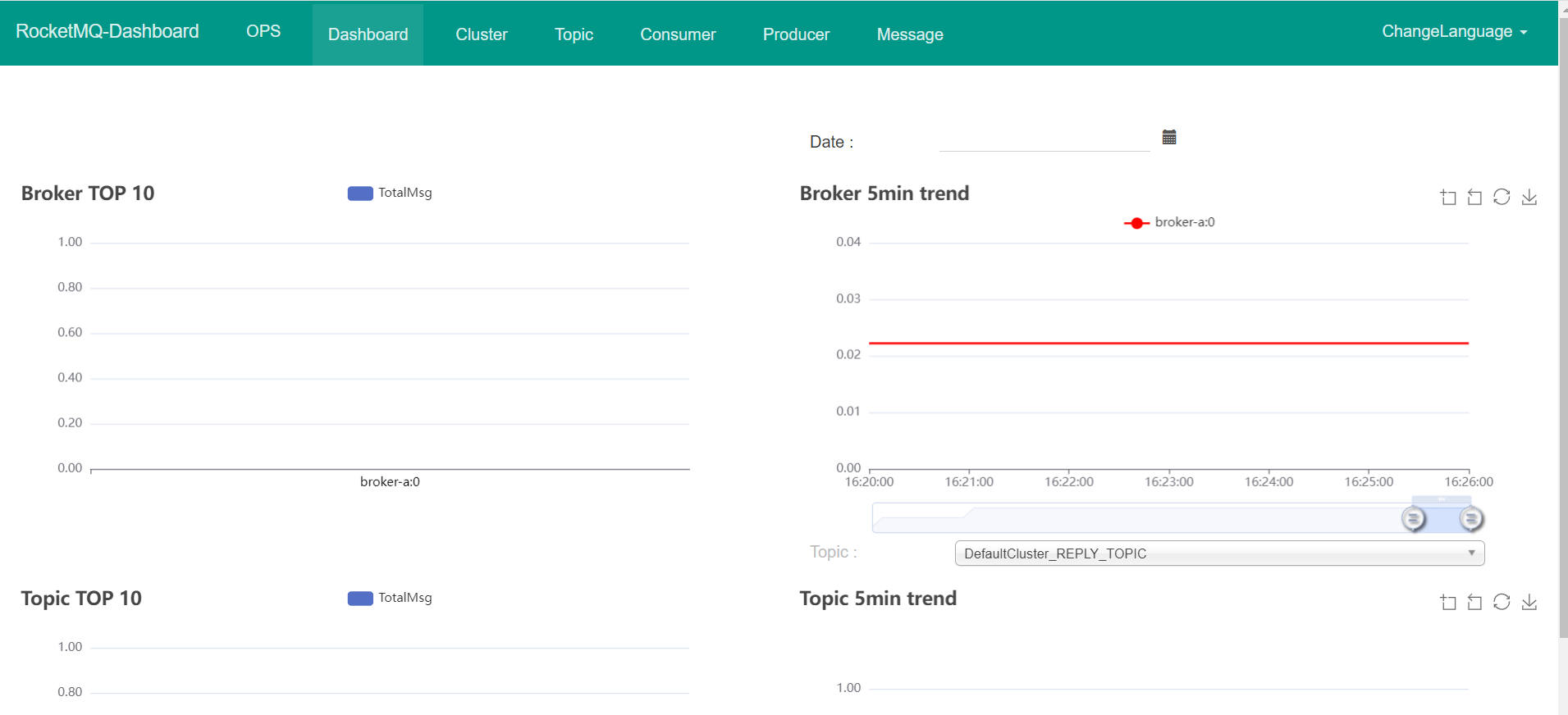
使用docker-compose部署RocketMQ5.0
简介:使用docker-compose部署rocketmq5.0。文中会介绍docker-compose版本以及需要注意的项第一步:进入hub.docker.com搜索rocketmq我们选择第一个,因为第一个是7个月前更新的,(我看有很多博客使用的依旧是最下面的那种…...

嵌入式ARM设计编程(四) ARM启动过程控制
文章和代码已归档至【Github仓库:hardware-tutorial】,需要的朋友们自取。或者公众号【AIShareLab】回复 嵌入式 也可获取。 一、实验目的 (1) 掌握建立基本完整的ARM 工程,包含启动代码,C语言程序等&…...

企业维基都说好,今天我们来看看 wiki 软件的缺点有哪些?
企业维基企业wiki和内部知识库可能看起来是一回事——但它们实际上是非常不同的软件类型。也许您可能不知道你在寻找的是知识基础软件,还是wiki软件。 无论哪种方式,缺乏知识都是生产力的巨大瓶颈。事实上,未能分享知识是财富500强企业每年亏…...
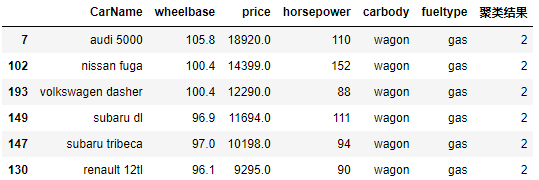
08- 汽车产品聚类分析综合项目 (机器学习聚类算法) (项目八)
找出性价比较高的车 LabelEncoder: python:sklearn标签编码(LabelEncoder) sklearn.preprocessing.LabelEncoder的使用:在训练模型之前,通常都要对数据进行一定得处理。将类别编号是一种常用的处理方法,比如把类别“电脑”,“手机…...

揭开苹果供应链,如何将其命运与中国深度捆绑
前 言 诺基亚在2007年时拥有9亿用户,在手机市场上占据主导地位,福布斯在当时以“谁能赶上手机之王?”为标题刊登了一篇关于该公司的报道,与此同时,苹果公司推出了iPhone系列产品。16年后,苹果公司以充足的…...
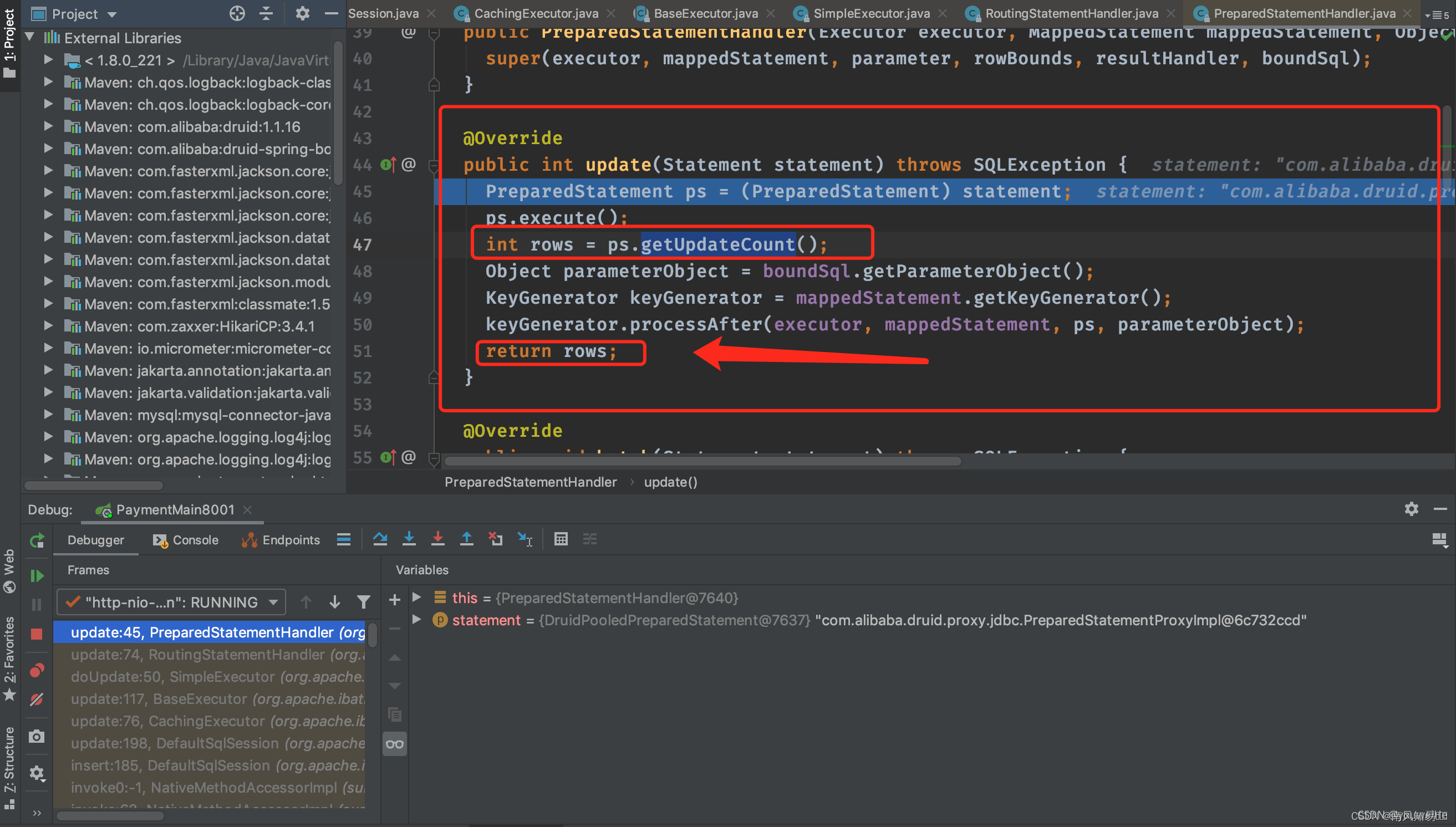
Mybatis 之useGeneratedKeys注意点
一.例子 Order.javapublic class Order {private Long id;private String serial; }orderMapper.xml<?xml version"1.0" encoding"UTF-8"?> <!DOCTYPE mapper PUBLIC "-//mybatis.org/DTD Mapper 3.0" "http://mybatis.org/dtd…...
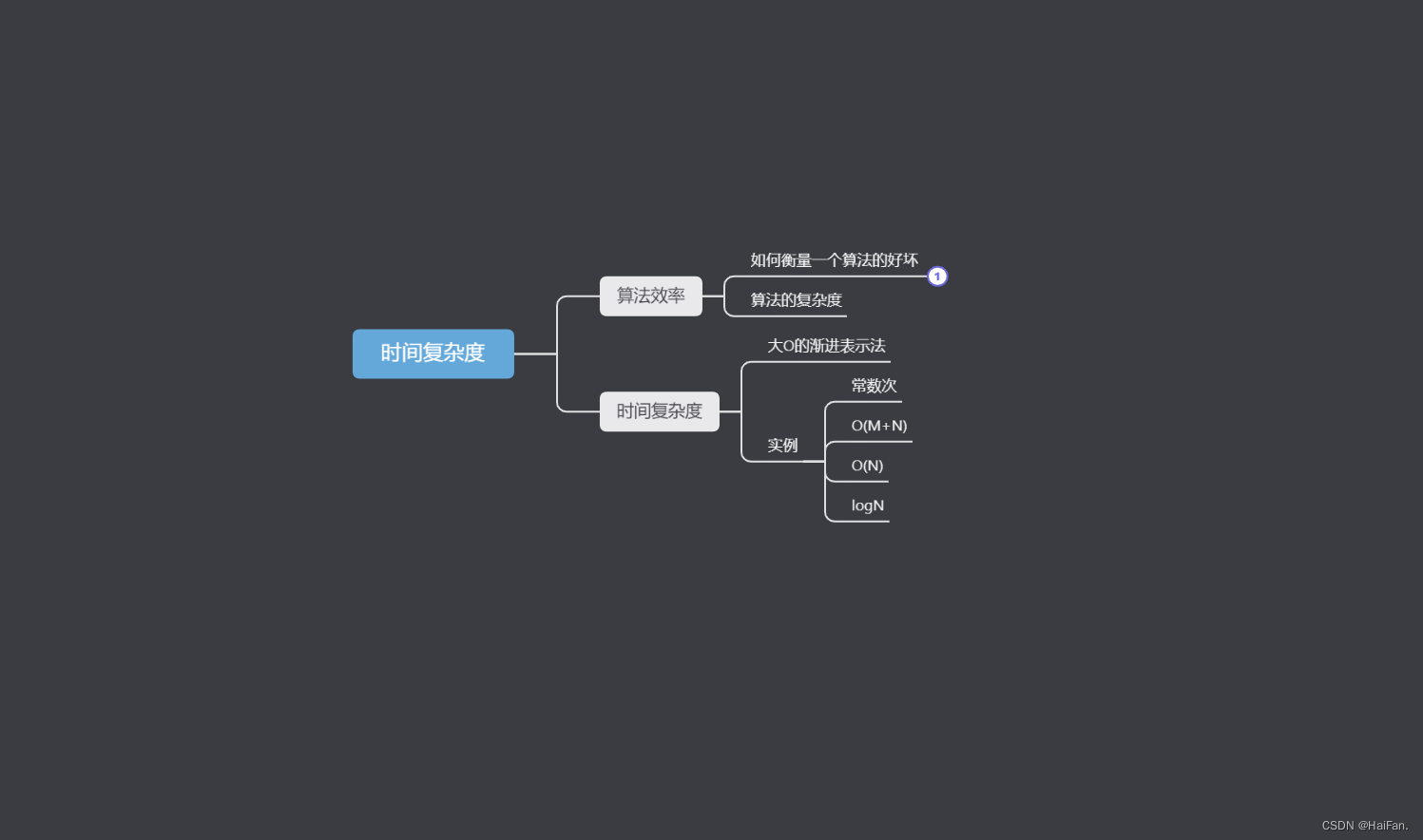
数据结构---时间复杂度
专栏:数据结构 个人主页:HaiFan. 专栏简介:开学数据结构,接下来会慢慢坑新数据结构的内容!!!! 时间复杂度前言1.算法效率1.1如何衡量一个算法的好坏1.2算法的复杂度2.时间复杂度2.1大…...

如何保证集合是线程安全的 ConcurrentHashMap如何实现高效地线程安全?
第10讲 | 如何保证集合是线程安全的? ConcurrentHashMap如何实现高效地线程安全? 我在之前两讲介绍了 Java 集合框架的典型容器类,它们绝大部分都不是线程安全的,仅有的线程安全实现,比如 Vector、Stack,在性能方面也…...

C++对象模型和this指针
成员变量和成员函数分开存储:基本概念:在C中,类内的成员变量和成员函数分开存储只有非静态成员变量才属于类的对象上每个空对象都会有一个独一无二的内存地址,所以,空对象占用内存空间的大小为1代码实现:#i…...
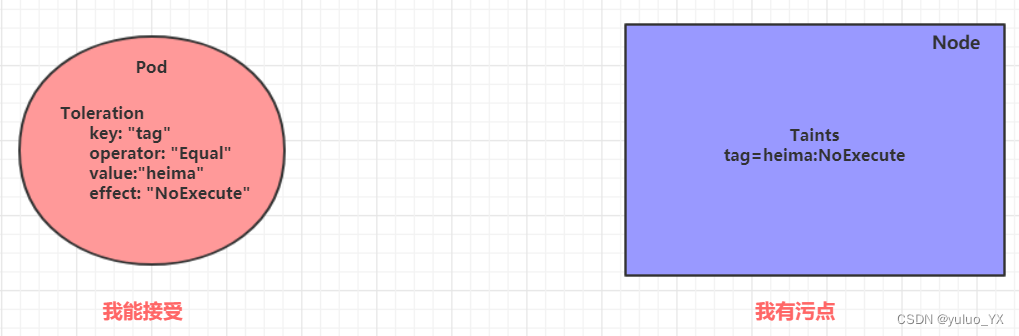
kubernetes教程 --Pod调度
Pod调度 在默认情况下,一个Pod在哪个Node节点上运行,是由Scheduler组件采用相应的算法计算出来的,这个过程是不受人工控制的。但是在实际使用中,这并不满足的需求,因为很多情况下,我们想控制某些Pod到达某…...

功率放大器科普知识(晶体管功率放大器的注意事项)
虽然功率放大器是电子实验室的常用仪器,但是很多人对于它却没有清晰的认识,下面就让安泰电子来为大家介绍功率放大器的科普内容以及使用注意事项,希望大家可以对功率放大器有清晰的认识。功率放大器可以把输入信号的功率放大,以满…...
CentOS 7转化系统为阿里龙蜥Anolis OS 7
转载:原社区CentOS 7迁移Anolis OS 7迁移手册 一、注意事项 Anolis OS 7生态上和依赖管理上保持跟CentOS7.x兼容,一键式迁移脚本centos2anolis.py,实现CentOS7.x到Anolis OS 7的平滑迁移。 使用迁移脚本前需要注意如下事项: 迁…...
【快速复习】一文看懂 Mysql 核心存储 隔离级别 锁 MVCC 机制
一文看懂 Mysql 核心存储 & 隔离级别 & 锁 & MVCC 机制 Mysql InnoDB 引擎下核心存储 数据&索引存储 IBD 文件 mysql 实际存储采用 B 树结构。 B 树是一种多路搜索树,其搜索性能高于 B 树 所有叶节点在同一深度,保证搜索效率仅叶节…...
面试题----集合
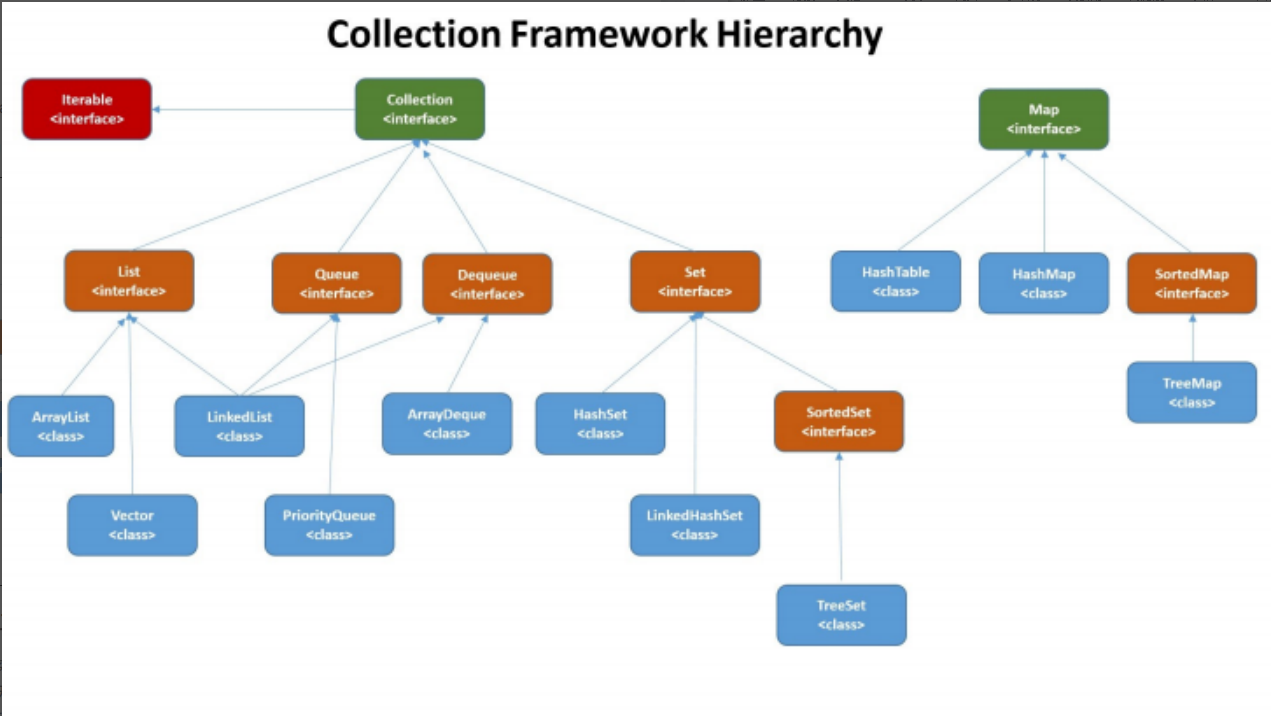
概述 从上图可以看出,在Java 中除了以 Map 结尾的类之外, 其他类都实现了 Collection 接⼝。 并且,以 Map 结尾的类都实现了 Map 接⼝List,Set,Map List (对付顺序的好帮⼿): 存储的元素是有序的、可重复的。 Set (注重独⼀⽆⼆…...
XSS注入基础入门篇
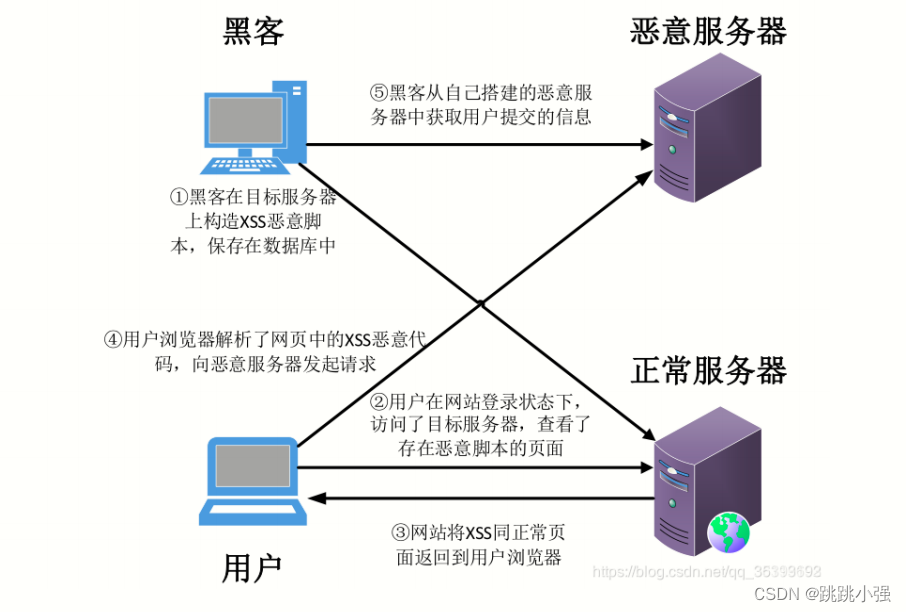
XSS注入基础入门篇1.XSS基础概念2. XSS的分类以及示例2.1 反射型XSS2.1.1 示例1:dvwa low 级别的反射型XSS2.1.2 攻击流程2.2 DOM型XSS2.2.1 示例2:DOM型XSS注入1.环境部署2.基础版本3.进阶绕过2.3 存储型XSS2.3.1 示例1:dvwa low示例2.3.2 攻…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...
