程序人生 - 学习和分享
文章目录
- 记于 230217
- 学习安排
- 泛学
- AI 和 未来
记于 230217
刚入行时,经常看到技术博客中,博主们分享生活,比如相亲、上班生活,甚至还有人发结婚照。这个栏目通常被称为:程序人生。
这个现象已经很久没看到了,原因大家都知道。比如互联网氛围不同了,从前多事 80后大牛;互联网刚兴起,大家会把博客、QQ空间,真的当做 小窝。从前大家会晒晒美食,现在朋友圈都没人发了。
挺怀念那个时代,文章有温度,看到了就像是感受到了真实的人;看到他们分享的学习/奋斗过程,会被激励、鼓舞信心,希望自己也能成为大佬。
学习始终是个逆流而行的事,需要目标、意志力、时间精力。
然而,当到了30岁+,会体会到那句话:当很多事情都变得很困难的时候,最简单的事就是 学习 和 减肥。
无论是婆媳关系、照顾年纪渐长的父母、带孩子,对于大部分人,都有很多痛苦,甚至是结构性的;我们难以改变别人,改变自己就变得容易。
改变的方向,当然是变得更强大。在有限的时间内,集中精力做重要的事,比如,做好专业。
经历了 测试 – iOS开发 – macOS 开发 – NLP 工程师的转变,NLP在不断变革,又走向了大模型的模式。
我好像还没扎稳脚跟,就快 35岁退休了。想想不禁有些沮丧。最宝贵的时间青春都在技术上了,但还走的不够高和深;最紧迫的 29–31岁,用来转行了,又穷又孤独。
说不后悔当然是假的。如果三五年后更好了,也许就不后悔了。后不后悔也许是动态的。
如果重新来一次(我觉得这个话题很有意义),我希望在大学把C++学好,多练习。
工作后,如果幸运,还是希望一个方向研究到底、研究的更深。然后花些时间在社科学习和交高质量(爱学习、善良)朋友上吧。
但时间无法回头,作为一个建设主义者,我选择重新规划路线:好好安排时间。
能够变现的叫做职业(希望能延长职业时间),不能变现的(再专业)也是爱好;这两个我都想要。
再次感谢认识的网友:李厂长,让我发现,时间可以这么安排、人生可以这么活,可以这么开心丰富和有趣。
大概是非计算机专业加上天生性格,在这个行业一直带着些焦虑。
刚毕业那时,爱吃爱喝爱拍照,玩烘焙花艺跳舞。而现在年轻人看到我,大概就是我从前看比我年长的人的样子吧 ----- 带着朴素和笨拙。
很多东西已经让我体会不到很大的快乐了,但学习,真的会让我安心。
这里分享下我的生活、学习和时间。
学习安排
学习内容
- 专业,围绕topic 进行看书、操作
- 专业相关,泛学 计算机各种知识
- 人文:历史、地理、社科、心理
时间
- 除了交通、睡眠、饮食,80%的时间我会花在学习上
- 周一到周五,我一般早上8点到公司,8:30 下班;早上多学1h,晚上多2h。
- 晚上到家,睡前可能看视频30min,或听书
- 周六到办公室 或图书馆学习一天
(在图书馆可以坐9个小时,是大学时期的我做不到的
学习方式
- 看书
- 看视频,B站超棒
- 练习
- 总结、写博客
人有不同的状态,适合不同的方式组合
- 早上清爽,看书
- 晚上精力不好时,总结所学
- 晚上可以延续下午学习的内容,进行练习和总结
- 在家洗完澡后,可以看视频学学
泛学
非计算机行业,好奇心求知欲又很强,每一样都学好、操作好,相当费时间;
也有人说,你这么辛苦总在忙,收获不大;抓好重点,会更有回报。
抓重点当然必须,但 东学习学 就是天生爱好啊!我不会放弃,只是换成 泛学。
今天刚好看到爱kk 说的一段话:
“我一直在倡导大家,一定要大量地泛读,哪怕你光看一个标题。有些东西实际上光看标题就足够了,尤其是新闻。技术性的东西,其实就是看角度,看思路,非常快速的。如果是你确实很感兴趣的,再去精读,一旦精读了就不要抱着泛读的心态。”
来源:https://www.sohu.com/a/242347855_99979179
我觉得很适合我呢。分享下我的泛学收获:
- 春节期间,我用两天了解完 Hadoop 生态;两天了解了 推荐系统;两天看了 ELK。
(B站的黑马程序员 真的是很棒的存在,讲的清晰干净,配套资料也很够。 - 曾经书架上大部头的书,前十页还留着从前的划线笔记,我用了一个下午(约4个小时),搞明白了它大概讲什么,我什么时候可能用到,用到的时候怎么查。
实际上,80%的技术书都是手册,知道了原理、有哪些API即可。
想想是不是就很开心呢?(我内心是个ENTJ)
如果2天能大致搞清一个技术,那还会对很多事感到未知和迷茫吗?
(如果可以,我还想尝试下 技术方案咨询之类的岗位呢。
学习,让我对生活了多了些掌控感;
泛学,让我对学习多了些自信。
学习,也是一个越学越会的过程;更了解自己的精力周期,更合理的安排学习内容。
打死也没想到,30岁之后的我,会变成一个爱学习的人;如果读书的时候也这样,我应该会去更好地学校吧?
所以,看到这里的小伙伴,我们一起加油好吗?欢迎分享给我你的学习过程、计划和成果,我也会觉得很开心的!
未来,我可能会在这里继续做一些生活的分享,就像以前钦佩的前辈一样。
技术的分享,可能深可能浅,大多会是学习后的总结(会注意版权)。
然后,分享下我常常自学的地方吧:



AI 和 未来
最后,分享下对 AI 和未来的看法
源自于(非专业领域)亲戚在家族群问我,chxxGPT 这么强大,会不会取代我们。
第一反应是短时间不会取代,很多东西还需要人工审核才行。同时如黄老师所说,围绕 AIGC 的安全性是个重要课题。
实际上,工业时代机器已经大幅取代了重复劳动力;AI的发展,已经有了心智化的趋势;某AI做的心理咨询,我觉得可以解决很多问题了。
人到底有什么是不可取代的? 身、心、灵,可能灵方面难以超越;但普通人有多少灵性呢?
论有效读书和输出能力,大部分人真的不如AI。
有时想想,人为什么不能被取代呢? 作为动物,那么多动物都灭绝,我们为什么不能呢。只是沿着惯性,活着就好好活着,生儿育女,有些羁绊。
从社会角度而言,人口有价值;但如果,高智能无限体力的机器,可以在少人口的情况下,发展处更强的生产力呢?
对于家庭,每个人都很重要;那么对于选择不结婚生子、或被婚恋市场淘汰的人呢? 人活着是为了什么?
你希望AI 带来什么?
2023-02-17(五)
相关文章:

程序人生 - 学习和分享
文章目录记于 230217学习安排泛学AI 和 未来记于 230217 刚入行时,经常看到技术博客中,博主们分享生活,比如相亲、上班生活,甚至还有人发结婚照。这个栏目通常被称为:程序人生。 这个现象已经很久没看到了,…...

基于树莓派的智能家居项目整理
一、功能介绍 二、设计框图 三、实物展示 四、程序 一、功能介绍硬件:树莓派3B、LD3320语音识别模块、pi 摄像头、继电器组、小灯、火焰传感器、蜂鸣器、电 磁锁 项目框架: 采用了简单工厂模式的一个设计方式。稳定,拓展性…...

《洛阳冬冷》
——洛阳的冬天太冷,最暖不过你的眼神。 ******* 她拿了个画着几丛竹子的小团扇子一路分花拂柳地往前走,后面一水儿的侍女不敢出声,只得地默默跟着她。她一张脸本来生得就好看,这一怒起来竟然还更加的好看了。此时她走得太急&…...
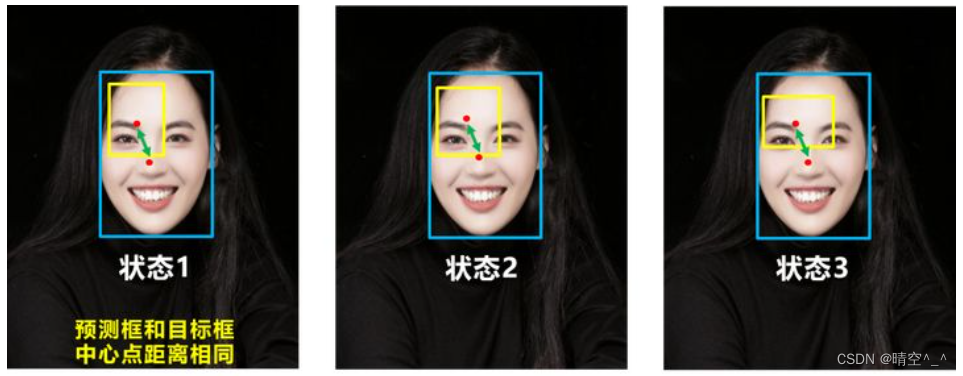
YOLOv5简介
YOLOv5 一、输入端 1. Mosaic数据增强: CutMix 数据增强:随机生成一个裁剪框Box,裁剪掉A图中的相应位置,然后用B图相应位置的ROI放到A中被裁剪的区域中形成新的样本。采用加权求和的方式计算损失,将A区域中被cut掉的…...
【面向对象语言三大特性之 “继承”】
目录 1.继承的概念及定义 1.1继承的概念 1.2 继承定义 1.2.1定义格式 1.2.2继承关系和访问限定符 1.2.3继承基类成员访问方式的变化 2.基类和派生类对象赋值转换 3.继承中的作用域 4.派生类的默认成员函数 5.继承与友元 6. 继承与静态成员 7.复杂的菱形继承及菱形虚拟…...
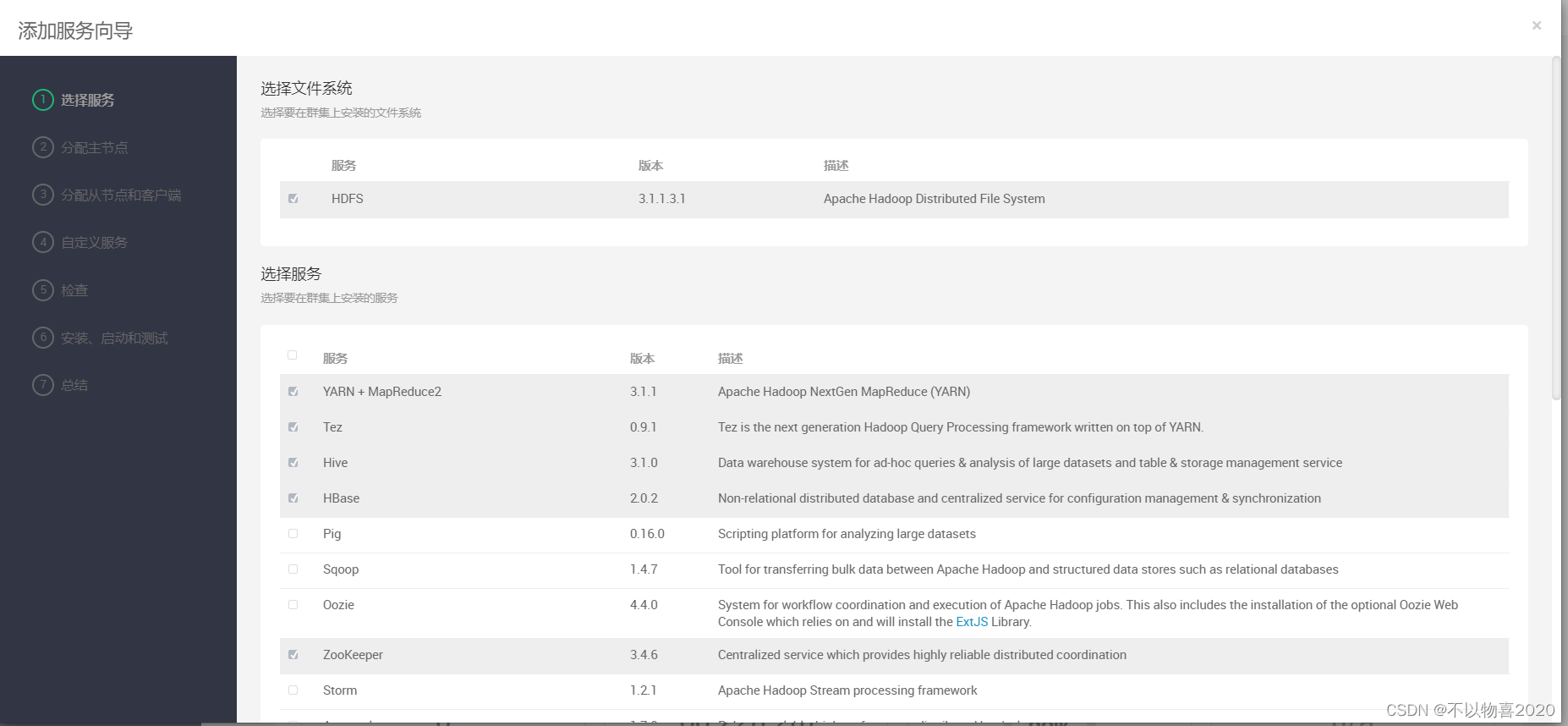
Ambari2.7.5集群搭建详细流程
0 说明 本文基于本地虚拟机从零开始搭建ambari集群 1 前置条件 1.1 本地虚拟机环境 节点角色ambari-1ambari-server ambari-agentambari-2ambari-agentambari-3ambari-agent 1.2 安装包 1.3 修改主机名并配置hosts文件 hostnamectl set-hostname ambari-1 hostnamectl se…...

房产|1月全国70城房价出炉!疫情放开后你关心的城市房价有何变化
2023年1月份,70个大中城市中新房销售价格环比上涨城市个数增加;一线城市新房销售价格环比同比转涨、二三线城市环比降势趋缓,二三线城市同比下降。 | 新房/二手房12月-1月环比上涨城市数量变化 70个大中城市中,新房环比上涨城市…...

秒验 重新定义“一键登录”
现如今,一般APP在注册登录时,仍然要经历填写用户名、密码、绑定手机号等一系列传统流程,有的人认为可以通过第三方登录避免这些流程,但仍旧要经历手机验证码的环节,而且存在验证码被拦截的风险,短信费用也很…...

ZenBuster:一款功能强大的多线程跨平台URL枚举工具
关于ZenBuster ZenBuster是一款功能强大的多线程跨平台URL枚举工具,该工具基于Python开发,同时还具备暴力破解功能。 该工具适用于安全专业人员,可以在渗透测试或CTF比赛中为广大研究人员提供帮助,并收集和目标相关的各种信息。…...

2023年美赛ICM问题E:光污染 这题很好做啊!
2023年美赛ICM问题E:光污染 这题很好做啊! 我看到DS数模的分析,看似头头是道,实则GouPi不通,我出一个,用于大家…...
)
InVEST模型 | 01 InVEST模型安装(Windows10)
除了在Python Anaconda环境中进行安装InVEST模型Python安装,平时最常使用的安装方式是通过.exe直接进行安装,本节介绍的就是直接下载安装的步骤: 打开InVEST模型下载页面 链接为:https://naturalcapitalproject.stanford.edu/…...
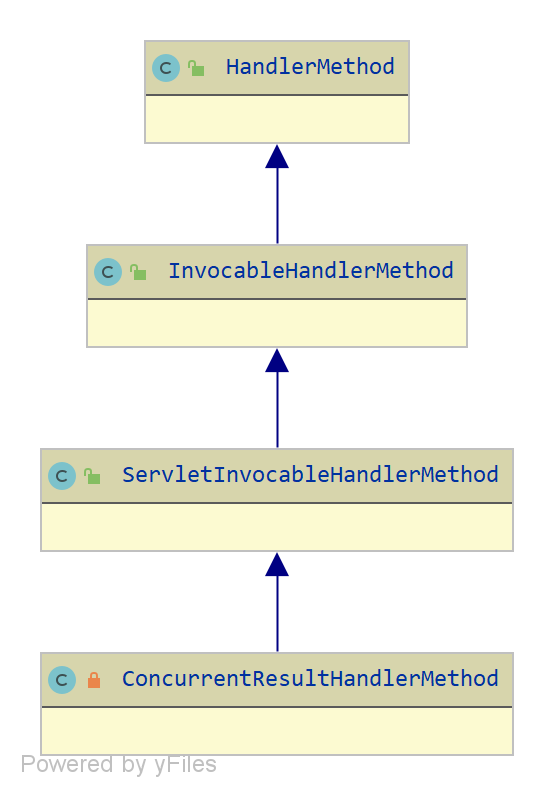
spring-web InvocableHandlerMethod 源码分析
说明 本文基于 jdk 8, spring-framework 5.2.x 编写。author JellyfishMIX - github / blog.jellyfishmix.comLICENSE GPL-2.0 类层次 HandlerMethod,处理器的方法的封装对象。HandlerMethod 只提供了处理器的方法的基本信息,不提供调用逻辑。 Invoca…...
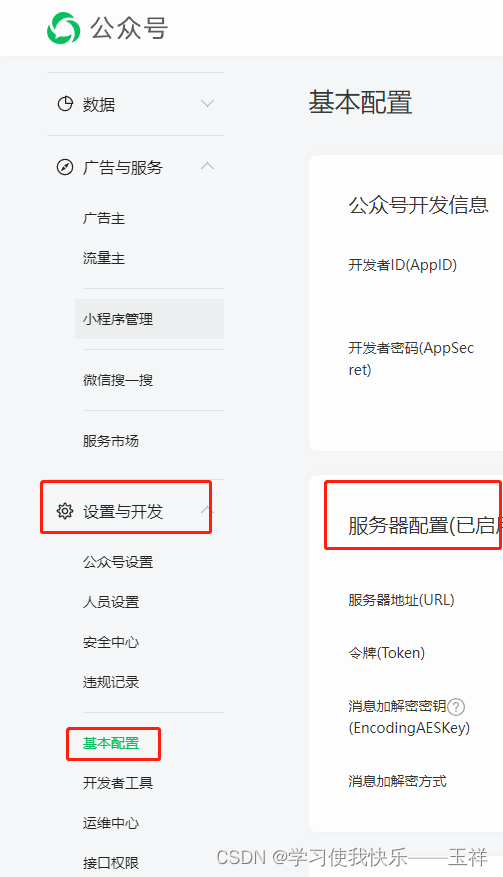
一分钟了解微信公众号服务器配置自动回复
1、建一个web服务工程 2、开放任意一个接口, 比如 /aaa/bbb/ccc 把接口路径配置在这里,ip为公网ip或域名,其他的参数默认,对入门选手没啥用 3、该接口允许get和post两种方式访问,接口需要对于访问方式编写两套逻辑…...

打印不同的图形-课后程序(JAVA基础案例教程-黑马程序员编著-第四章-课后作业)
【案例4-1】打印不同的图形 记得 关注,收藏,评论哦,作者将持续更新。。。。 【案例介绍】 案例描述 本案例要求编写一个程序,可以根据用户要求在控制台打印出不同的图形。例如,用户自定义半径的圆形和用户自定义边长的…...

14. QT_OPenGL中引入顶点着色器和片段着色器
1. 说明: 着色器是OPenGL中非常重要的一部分,在有了模型后,如果未给模型添加着色器,那么渲染效果会折扣很多。着色器中使用到的语言是GLSL(OPenGL Shader Language),可以通过这篇文章GLSL基本语法进行了解。 效果展示:…...
ecaozzz
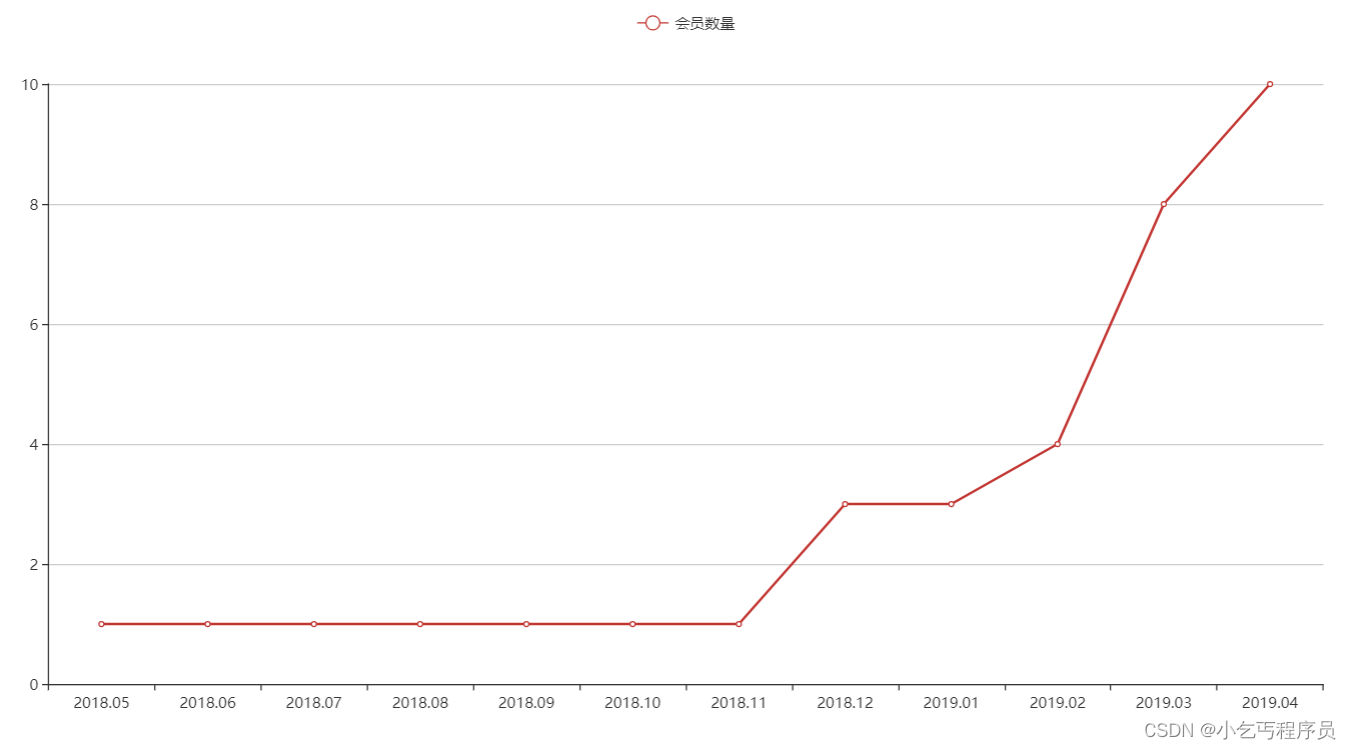
2. 图形报表ECharts 2.1 ECharts简介 ECharts缩写来自Enterprise Charts,商业级数据图表,是百度的一个开源的使用JavaScript实现的数据可视化工具,可以流畅的运行在 PC 和移动设备上,兼容当前绝大部分浏览器(IE8/9/10/…...
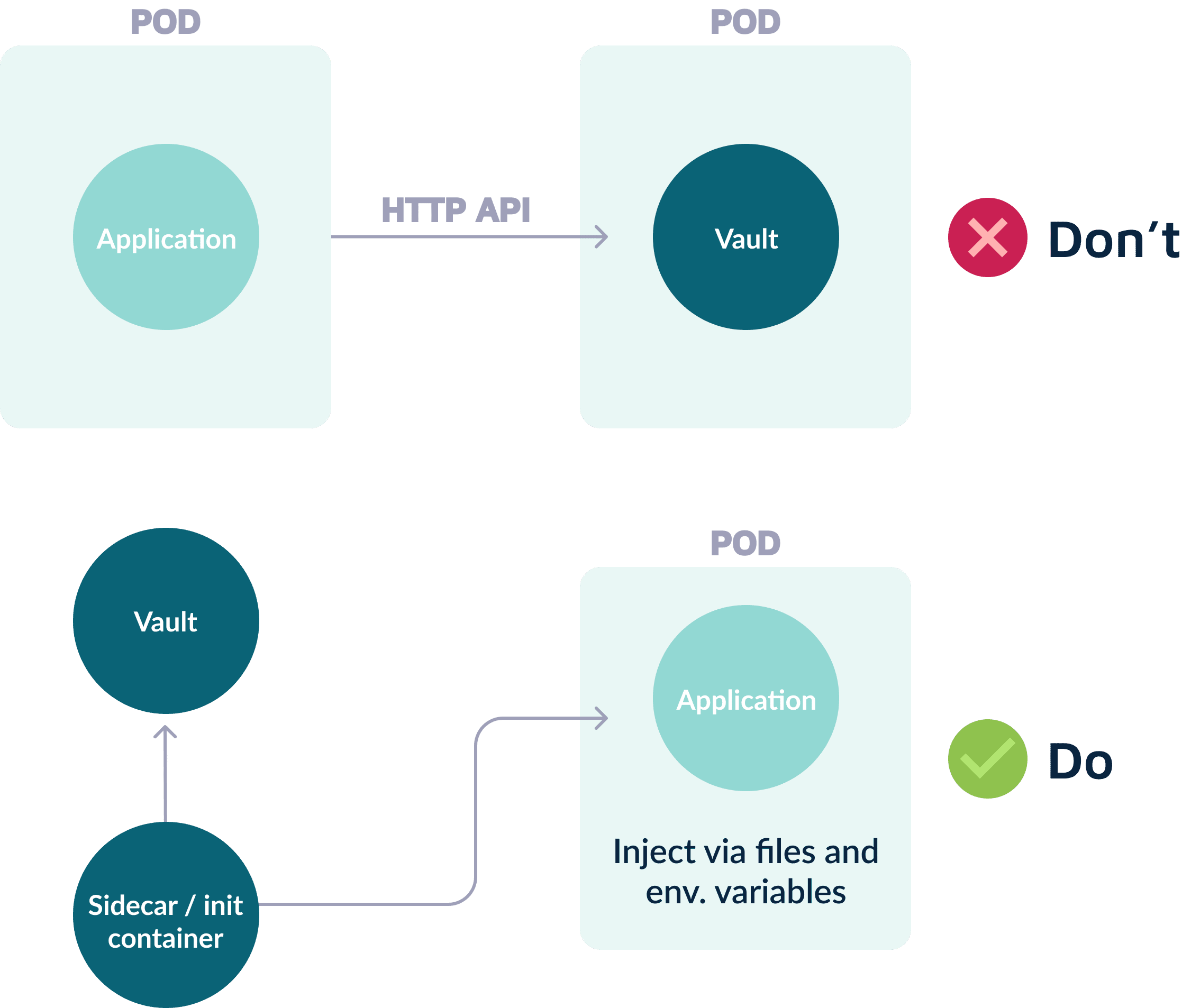
应用部署初探:6个保障安全的最佳实践
在之前的文章中,我们了解了应用部署的阶段以及常见的部署模式,包括微服务架构的应用应该如何部署等基本内容。本篇文章将介绍如何安全地部署应用程序。 安全是软件开发生命周期(SDLC)中的关键部分,同时也需要成为 S…...
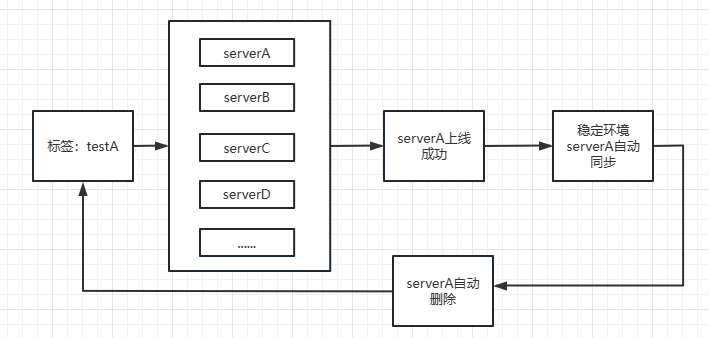
转转测试环境docker化实践
测试环境对于任何一个软件公司来讲,都是核心基础组件之一。转转的测试环境伴随着转转的发展也从单一的几套环境发展成现在的任意的docker动态环境docker稳定环境环境体系。期间环境系统不断的演进,去适应转转集群扩张、新业务的扩展,走了一些…...

linux 之 ps命令介绍
哈喽,大家好,我是有勇气的牛排(全网同名)🐮 有问题的小伙伴欢迎在文末评论,点赞、收藏是对我最大的支持!!!。 前言 如过想实现对进程监控,就需要使用到ps命…...

Server端的Actor,分工非常的明确,但是只将Actor作为一部手机来用,真的合适吗?
这是一篇介绍PowerJob,Server端Actor的文章,如果感兴趣可以请点个关注,大家互相交流一下吧。 server端一共有两个Actor,一个是处理worker传过来的信息,一个是server之间的信息传递。 处理Worker的Actor叫做WorkerRequ…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

uniapp 实现腾讯云IM群文件上传下载功能
UniApp 集成腾讯云IM实现群文件上传下载功能全攻略 一、功能背景与技术选型 在团队协作场景中,群文件共享是核心需求之一。本文将介绍如何基于腾讯云IMCOS,在uniapp中实现: 群内文件上传/下载文件元数据管理下载进度追踪跨平台文件预览 二…...

论文阅读:Matting by Generation
今天介绍一篇关于 matting 抠图的文章,抠图也算是计算机视觉里面非常经典的一个任务了。从早期的经典算法到如今的深度学习算法,已经有很多的工作和这个任务相关。这两年 diffusion 模型很火,大家又开始用 diffusion 模型做各种 CV 任务了&am…...

boost::filesystem::path文件路径使用详解和示例
boost::filesystem::path 是 Boost 库中用于跨平台操作文件路径的类,封装了路径的拼接、分割、提取、判断等常用功能。下面是对它的使用详解,包括常用接口与完整示例。 1. 引入头文件与命名空间 #include <boost/filesystem.hpp> namespace fs b…...

MeshGPT 笔记
[2311.15475] MeshGPT: Generating Triangle Meshes with Decoder-Only Transformers https://library.scholarcy.com/try 真正意义上的AI生成三维模型MESHGPT来袭!_哔哩哔哩_bilibili GitHub - lucidrains/meshgpt-pytorch: Implementation of MeshGPT, SOTA Me…...
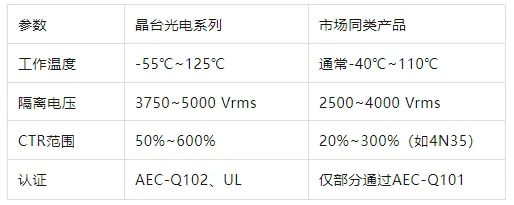
高抗扰度汽车光耦合器的特性
晶台光电推出的125℃光耦合器系列产品(包括KL357NU、KL3H7U和KL817U),专为高温环境下的汽车应用设计,具备以下核心优势和技术特点: 一、技术特性分析 高温稳定性 采用先进的LED技术和优化的IC设计,确保在…...

python基础语法Ⅰ
python基础语法Ⅰ 常量和表达式变量是什么变量的语法1.定义变量使用变量 变量的类型1.整数2.浮点数(小数)3.字符串4.布尔5.其他 动态类型特征注释注释是什么注释的语法1.行注释2.文档字符串 注释的规范 常量和表达式 我们可以把python当作一个计算器,来进行一些算术…...

【汇编逆向系列】六、函数调用包含多个参数之多个整型-参数压栈顺序,rcx,rdx,r8,r9寄存器
从本章节开始,进入到函数有多个参数的情况,前面几个章节中介绍了整型和浮点型使用了不同的寄存器在进行函数传参,ECX是整型的第一个参数的寄存器,那么多个参数的情况下函数如何传参,下面展开介绍参数为整型时候的几种情…...
)
iOS 项目怎么构建稳定性保障机制?一次系统性防错经验分享(含 KeyMob 工具应用)
崩溃、内存飙升、后台任务未释放、页面卡顿、日志丢失——稳定性问题,不一定会立刻崩,但一旦积累,就是“上线后救不回来的代价”。 稳定性保障不是某个工具的功能,而是一套贯穿开发、测试、上线全流程的“观测分析防范”机制。 …...
