全期望值定理与全方差定理
全期望值定理(law of total expectation)比较熟悉,竟然还有个全方差定理(law of total variance),关于条件期望与条件方差的,总结一下。
1. 全期望值定理
随机变量 XXX 关于另外一个随机变量 YYY 的条件方差的期望的期望等于该随机变量 XXX 的期望
E(X)=EY[E(X∣Y)]E(X)=E_Y[E(X|Y)] E(X)=EY[E(X∣Y)]
2. 全方差定理
这个就稍微有点复杂了
Var(X)=EY(Var(Y∣X))+VarY(E(Y∣X))Var(X)=E_Y(Var(Y|X))+Var_Y(E(Y|X)) Var(X)=EY(Var(Y∣X))+VarY(E(Y∣X))
证明:
先把方差表示成期望形式,利用全期望值定理,然后将第一项期望值展开,最后把后两项期望值结合
Var(X)=E(X2)−E2(X)=EY[E(X2∣Y)]−{EY[E(X∣Y)]}2=EY[Var(X∣Y)+E2(X∣Y)]−{EY[E(X∣Y)]}2=EY[Var(X∣Y)+EY[E2(X∣Y)]−{EY[E(X∣Y)]}2=EY(Var(X∣Y))+VarY(E(X∣Y))\begin{aligned} Var(X)=&E(X^2)-E^2(X)\\ =&E_Y[E(X^2|Y)]-\{E_Y[E(X|Y)]\}^2\\ =&E_Y[Var(X|Y)+E^2(X|Y)]-\{E_Y[E(X|Y)]\}^2\\ =&E_Y[Var(X|Y)+E_Y[E^2(X|Y)]-\{E_Y[E(X|Y)]\}^2\\ =&E_Y(Var(X|Y))+Var_Y(E(X|Y)) \end{aligned} Var(X)=====E(X2)−E2(X)EY[E(X2∣Y)]−{EY[E(X∣Y)]}2EY[Var(X∣Y)+E2(X∣Y)]−{EY[E(X∣Y)]}2EY[Var(X∣Y)+EY[E2(X∣Y)]−{EY[E(X∣Y)]}2EY(Var(X∣Y))+VarY(E(X∣Y))
要能看出最后两项其实是 E(X∣Y)E(X|Y)E(X∣Y) 在 YYY 上的方差。 □\square□
相关文章:

全期望值定理与全方差定理
全期望值定理(law of total expectation)比较熟悉,竟然还有个全方差定理(law of total variance),关于条件期望与条件方差的,总结一下。 1. 全期望值定理 随机变量 XXX 关于另外一个随机变量 …...
)
股票的最大利润 AcWing (JAVA)
假设把某股票的价格按照时间先后顺序存储在数组中,请问买卖 一次 该股票可能获得的利润是多少? 例如一只股票在某些时间节点的价格为 [9,11,8,5,7,12,16,14]。 如果我们能在价格为 5 的时候买入并在价格为 16 时卖出,则能收获最大的利润 11。…...

Go 语言函数调用参数传递规则
1. 调试环境Go 版本:1.19.3Gdb 版本:12.1CPU 架构:amd64Linux 发行版:Ubuntu 22.04Linux 内核版本:5.15.0-482. 函数调用参数传递规则版本变化在 Go 中函数间进行调用时,主调(caller)…...

二分查找【零神基础精讲】
来源0x3f:https://space.bilibili.com/206214 文章目录二分查找[34. 在排序数组中查找元素的第一个和最后一个位置](https://leetcode.cn/problems/find-first-and-last-position-of-element-in-sorted-array/)[162. 寻找峰值](https://leetcode.cn/problems/find-p…...

「计算机组成原理」数据的表示和运算(上)
文章目录一、进位计数制1.1 其他进制转十进制1.2 十进制转其他进制1.3 二进制、八进制和十六进制1.3 真值和机器数二、BCD码2.1 8421码2.2 余3码2.3 2421码三、整数的表示和运算3.1 无符号整数3.1.1 无符号整数的表示3.1.2 无符号整数的运算3.2 有符号整数3.2.1 有符号整数的表…...

分层,均质,稀薄燃烧
均质燃烧: 只能使用火花点燃。 即为普通燃烧方式,燃料和空气混合形成一定浓度的可燃混合气(厂家自配),整个燃烧室内混合气的空燃比是相同的,经火花塞点燃燃烧。这种燃烧方式使燃料和空气充分混合,燃料完全燃烧,从而获得大的输出功率。为使混合…...
)
mybatis-plus小课堂:多表查询【案例篇】(apply 拼接 in SQL,来查询从表某个范围内的数据)
文章目录 引言I 多表查询1.1 多表查询:在mapper.xml 写语句和拼接查询条件1.2 多表关联:Java代码中书写语句和拼接查询条件1.3 案例:左外连接II mybatis-Plus 之 apply 拼接 in SQL2.1 apply源码实现2.2 apply 拼接 in SQLIII 常见问题3.1 Cause: comColumn xxx in where cl…...
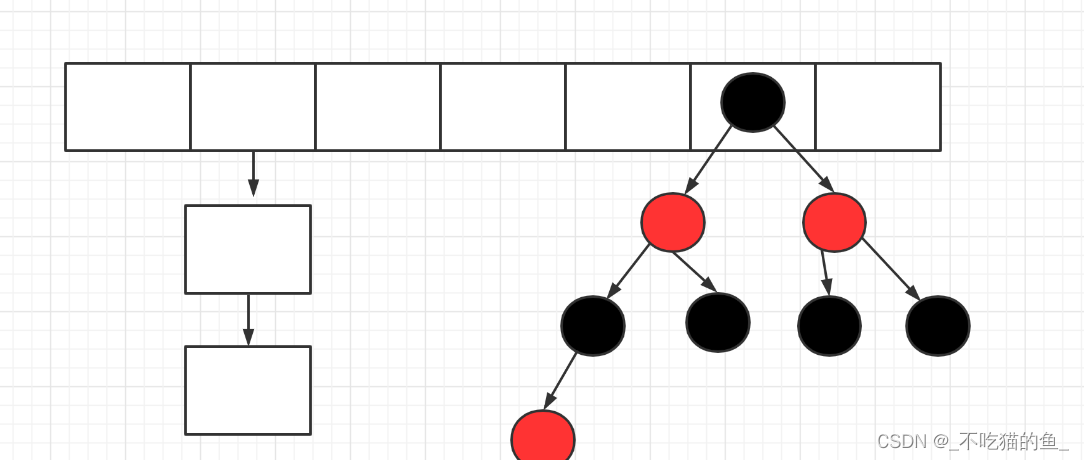
HashMap原理详解
一、hashmap简介 hashmap是Java当中一种数据结构,是一个用于存储Key-Value键值对的集合,每一个键值对也叫作Entry。 二、JDK7的HashMap1、JDK7时HashMap的数据结构 1、在JDK7之前,hashmap底层采用数组链表的数据结构来存储数据 2、插入数据采…...
推荐3款远程办公软件
一款好用的远程办公软件能够大大的提高我们的办公效率,在这篇文章中,我们将为您推荐几款常见又好用的远程办公软件,以帮助您能更加高效的远程办公。电脑远程办公软件有很多,本文主要从团队沟通软件、视频会议软件、远程控制软件等…...
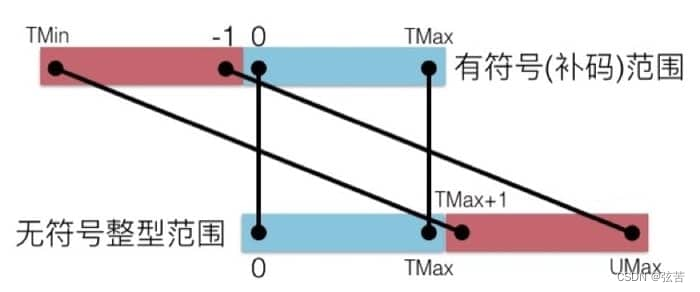
计算机中有符号数的表示
文章目录二进制数制十进制二进制位模式基本数据类型无符号数的编码有符号数的编码原码(Sign-Magnitude)反码(Ones Complement)补码(Twos Complement)概念导读编码格式按权展开补码加法扩展一个数字的位表示…...
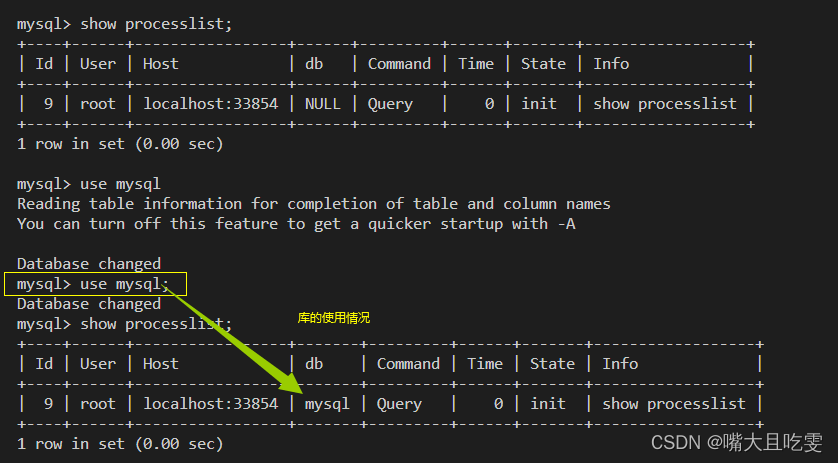
MySQL(一)服务器连接 库的基本操作
目录 一、连接服务器 二、简单使用 三、校验规则 条件筛选 where 进行order排序 三、查看数据库 使用 show databases;(注意分号和最后一个s) 显示创建数据库的详情信息:使用show create database test2; 四、修改数据库 五…...
Maven怎样构建生命周期?
项目构建生命周期Maven的本质是一个项目管理工具,将项目开发和管理过程抽象成一个项目对象模型(POM)。Maven构建生命周期描述的是一次构建过程经历经历了多少个事件。对项目构建的生命周期划分为3套,其中clean负责清理工作,default负责核心工…...
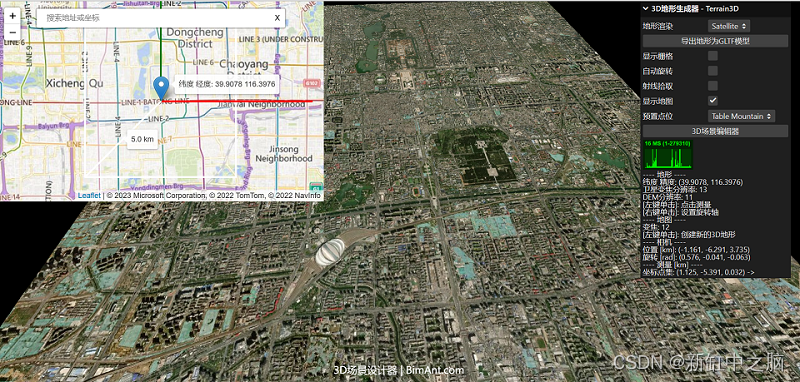
真实3D地形生成器【免费在线】
Terrain3D是一个免费的在线3D地形生成器,只需指定地球上的坐标,就可以自动生成附近区域的3D地形同时叠加卫星影像,并且可以导出GLTF格式的3D地形模型。 推荐:使用 NSDT场景设计器 快速搭建 3D场景。 使用Terrain3D生成真实世界的3…...
)
华为OD机试 - 整数编码(Python)
整数编码 题目 实现一个整数编码方法 使得待编码的数字越小 编码后所占用的字节数越小 编码规则如下 编码时7位一组,每个字节的低 7 位用于存储待编码数字的补码字节的最高位表示后续是否还有字节,置1表示后面还有更多的字节,置0表示当前字节为最后一个字节采用小端序编码…...

【GlobalMapper精品教程】051:融合Dissolve操作详解
本节讲解globalmapper中融合Dissolve工具的使用。 文章目录 一、工具介绍1. 工具位置2. 融合工具二、案例实战1. 加载实验数据2. 根据字段分组融合案例一:根据地类名称分组,将相同的类型融合到一起。案例二:根据权属地类名称分组,将相同的类型融合到一起。一、工具介绍 1.…...

Java Excel的数据导入导出
引入依赖 <!-- EasyExcel --> <dependency><groupId>com.alibaba</groupId><artifactId>easyexcel</artifactId><version>2.2.7</version> </dependency><!--csv文件操作--> <dependency><groupId>n…...
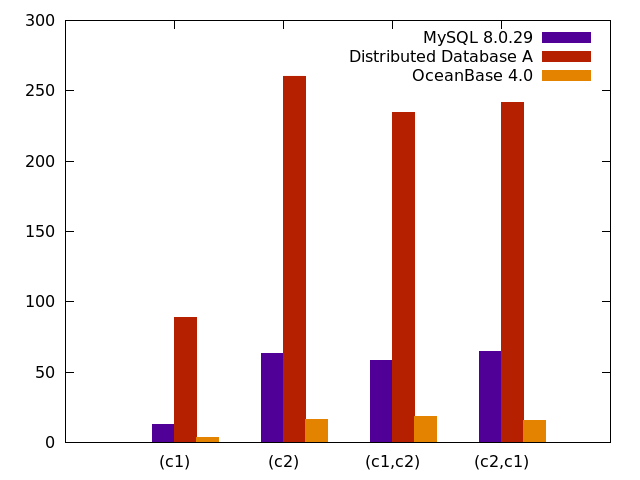
OceanBase 4.0解读:兼顾高效与透明,我们对DDL的设计与思考
关于作者 谢振江,OceanBase 高级技术专家。 2015年加入 OceanBase, 从事存储引擎相关工作,目前在存储-索引与 DDL 组,负责索引,DDL 和 IO 资源调度相关工作。 回顾关系型数据库大规模应用以来的发展,从单机到分布式无…...

Qt线程池
目录1、线程池是什么?2、Qt线程池2.1、用法例程2.2、线程池对性能的提升2.3、运行算法单线程写法线程池写法1、线程池是什么? 线程池是一种线程使用模式,它管理着一组可重用的线程,可以处理分配过来的可并发执行的任务。 线程池设…...

设置table中的tbody
<!DOCTYPE html> <html> <head> <meta charset"utf-8"> <title>设置table中的tbody</title> </head> <body> <script> // 这里有json数据,是jav…...
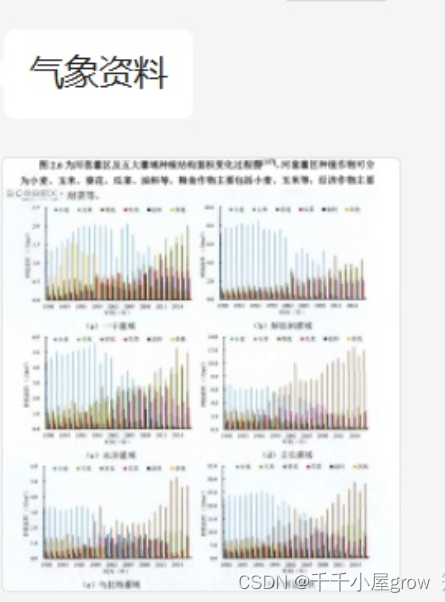
2023美赛A题完整数据!思路代码数据数学建模
选取内蒙古河套灌区(典型干旱区)2010-2020年气温,降雨,蒸散发和水汽压月数据 包括四种主要作物及其占比 内容截图如下: 链接为:https://www.jdmm.cc/file/2708703 同时还提供参考代码和参考文章的选项~…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

Caliper 配置文件解析:fisco-bcos.json
config.yaml 文件 config.yaml 是 Caliper 的主配置文件,通常包含以下内容: test:name: fisco-bcos-test # 测试名称description: Performance test of FISCO-BCOS # 测试描述workers:type: local # 工作进程类型number: 5 # 工作进程数量monitor:type: - docker- pro…...

华为OD机试-最短木板长度-二分法(A卷,100分)
此题是一个最大化最小值的典型例题, 因为搜索范围是有界的,上界最大木板长度补充的全部木料长度,下界最小木板长度; 即left0,right10^6; 我们可以设置一个候选值x(mid),将木板的长度全部都补充到x,如果成功…...

Chrome 浏览器前端与客户端双向通信实战
Chrome 前端(即页面 JS / Web UI)与客户端(C 后端)的交互机制,是 Chromium 架构中非常核心的一环。下面我将按常见场景,从通道、流程、技术栈几个角度做一套完整的分析,特别适合你这种在分析和改…...

Python 训练营打卡 Day 47
注意力热力图可视化 在day 46代码的基础上,对比不同卷积层热力图可视化的结果 import torch import torch.nn as nn import torch.optim as optim from torchvision import datasets, transforms from torch.utils.data import DataLoader import matplotlib.pypl…...

Java 与 MySQL 性能优化:MySQL 慢 SQL 诊断与分析方法详解
文章目录 一、开启慢查询日志,定位耗时SQL1.1 查看慢查询日志是否开启1.2 临时开启慢查询日志1.3 永久开启慢查询日志1.4 分析慢查询日志 二、使用EXPLAIN分析SQL执行计划2.1 EXPLAIN的基本使用2.2 EXPLAIN分析案例2.3 根据EXPLAIN结果优化SQL 三、使用SHOW PROFILE…...

嵌入式面试常问问题
以下内容面向嵌入式/系统方向的初学者与面试备考者,全面梳理了以下几大板块,并在每个板块末尾列出常见的面试问答思路,帮助你既能夯实基础,又能应对面试挑战。 一、TCP/IP 协议 1.1 TCP/IP 五层模型概述 链路层(Link Layer) 包括网卡驱动、以太网、Wi‑Fi、PPP 等。负责…...
