实验07 赫夫曼编码及综合2022(带程序填空)
A. 【程序填空】赫夫曼编码
题目描述
给定n个叶子的权值,根据这些权值构造huffman树,并输出huffman编码
参考课本第6.6节的算法6.12,注意算法中数组访问是从位置1开始
赫夫曼构建中,默认左孩子权值不大于右孩子权值
如果遇到两个孩子权值相等,那么按输入顺序或生成顺序来排列。
例如有一个叶子权值是29,后来生成一个中间结点权值也是29,那么叶子为左孩子,中间结点为右孩子
例如有两个叶子权值都是4,那么按输入顺序,先输入权值的叶子是左孩子
请完成以下程序填空
输入
第1行输入n,表示有n个叶子
第2行输入n个权值,权值都是正整数
输出
输出n行,每行输出格式:权值-赫夫曼编码
请参考样例
输入:
8
5 29 7 8 14 23 3 11输出:
5-0001
29-10
7-1110
8-1111
14-110
23-01
3-0000
11-001代码:
#include <iostream>
#include <cstring>
#include <string>
#include <sstream>
using namespace std;const int maxW = 9999; //设定无穷大权值//Huffman树结点结构
class HuffNode { //哈夫曼树的结点结构
public:int weight; //权值int parent; //双亲下标int lchild; //左孩子下标int rchild; //右孩子下标
};//Huffman树结构
class HuffMan {
private:int len; //结点总数,等于lnum*2-1int lnum; //叶子数量HuffNode *HuffTree; //保存构建后的赫夫曼树信息void selectMin(int n, int &x1, int &x2);
//函数selectMin是从已生成的n个结点中(包含叶子),选出未选的且权值最小的两个结点的下标
//两个下标结果保存在x1和x2中
//第一小权值的结点下标保存在x1,第二小权值的结点下标保存在x2
//如果不想用这个函数,就在类外定义中定义一个空函数体,避免语法错误string *HuffCode; //保存叶子的赫夫曼编码char ** HC; //保存叶子的赫夫曼编码
//如果不喜欢用string,可以用二维字符数组HC
//HuffCode和HC,两者只用一个保存赫夫曼编码就可以了 public:HuffMan(int n,int w[]); //输入叶子数量和叶子权重,初始化HuffTree和HuffCode(或HC)void buildTree(); //构建赫夫曼树,保存在HuffTree中void Coding(); //生成赫夫曼编码,保存在HuffCode或HC中void printCode(); //输出赫夫曼编码~HuffMan(); //回收空间
};//请完成Huffman树的剩下部分类定义
HuffMan ::~HuffMan() {delete[]HuffTree;delete[]HuffCode;len = 0; lnum = 0;
}void HuffMan::selectMin(int n, int& x1, int& x2) {int j;x1 = 0; x2 = 0;for (j = 1; j < n; j++) {if (HuffTree[j].parent == 0) {if (x1 == 0)x1 = j;else if (x2 == 0) x2 = j;if (HuffTree[j].weight < HuffTree[x1].weight) {x2 = x1; x1 = j;}else if (x2 != 0 && HuffTree[j].weight < HuffTree[x2].weight) x2 = j;}}
}HuffMan::HuffMan(int n, int w[]) {lnum = n;len = 2 * lnum - 1;HuffTree = new HuffNode[len + 1];HuffCode = new string[lnum + 1];//位置从1开始int i = 1;for (i = 1; i <= len; i++) {HuffTree[i].weight = 0;HuffTree[i].lchild = 0;HuffTree[i].rchild = 0;HuffTree[i].parent = 0;}for (i = 1; i <= lnum; i++)HuffTree[i].weight = w[i - 1];
}void HuffMan::buildTree() {int x1, x2;for (int i = lnum + 1; i <= len; i++) {selectMin(i, x1, x2);HuffTree[x1].parent = i;HuffTree[x2].parent = i;HuffTree[i].lchild = x1;HuffTree[i].rchild = x2;HuffTree[i].weight = HuffTree[x1].weight + HuffTree[x2].weight;}
}void HuffMan::Coding() {int i, j, c, f; // c,f是结点在数组中的下标for (i = 1; i <= lnum; i++) { // c,f是结点在数组中的下标for (c = i, f = HuffTree[i].parent; f != 0; c = f, f = HuffTree[f].parent) {if (c == HuffTree[f].lchild) HuffCode[i] = '0' + HuffCode[i];else HuffCode[i] = '1' + HuffCode[i];}}
}void HuffMan::printCode() {for (int i = 1; i <= lnum; i++)cout << HuffTree[i].weight << "-" << HuffCode[i] << endl;
}
//主函数如下
int main(void)
{ int n, wt[100];cin>>n;for(int i=0;i<n;i++)cin>>wt[i];HuffMan huff(n,wt);huff.buildTree();huff.Coding();huff.printCode();return 0;
}B. 【程序填空】赫夫曼解码
题目描述
在掌握赫夫曼树构建的基础上,实现赫夫曼解码
赫夫曼构建中,默认左孩子权值不大于右孩子权值
如果遇到两个孩子权值相等,那么按输入顺序或生成顺序来排列。
例如有一个叶子权值是29,后来生成一个中间结点权值也是29,那么叶子为左孩子,中间结点为右孩子
例如有两个叶子权值都是4,那么按输入顺序,先输入权值的叶子是左孩子
请完成以下程序填空
输入
第一行输入n,表示有n个叶子
第二行输入n个叶子权值,权值全是正整数
第三行输入n个叶子对应的字符,权值全是正整数
第四行输入k,表示要输入k个编码串
接着输入k个编码串
输出
输出k行,每行输出一个编码串的解码结果。
如果编码串非法,则对应的一行输出error,不输出已解码的字符
输入:
5
15 4 4 3 2
K G C M W
2
11011010000001
0000011100010输出:
KKCGWM
error代码:
#include <iostream>
#include <string>
using namespace std;const int maxW = 9999; //设定无穷大权值//Huffman树结点结构
class HuffNode { //哈夫曼树的结点结构
public:char letter;//结点对应的字符int weight; //权值int parent; //双亲下标int lchild; //左孩子下标int rchild; //右孩子下标
};//Huffman树结构
class HuffMan {
private:int len; //结点总数,等于lnum*2-1int lnum; //叶子数量HuffNode *HuffTree; //保存构建后的赫夫曼树信息void selectMin(int n, int &x1, int &x2);
//函数selectMin是从已生成的n个结点中(包含叶子),选出未选的且权值最小的两个结点的下标
//两个下标结果保存在x1和x2中
//第一小权值的结点下标保存在x1,第二小权值的结点下标保存在x2
//如果不想用这个函数,就在类外定义中定义一个空函数体,避免语法错误public:HuffMan(int n,int w[], char c[]);
//构造函数HuffMan根据输入叶子数量、叶子权重、字符集合,初始化HuffTreevoid buildTree(); //构建赫夫曼树,保存在HuffTree中void Decoding(string cs);
//函数Decoding是根据参数编码串cs进行赫夫曼解码
//如果编码串cs有错,函数Decoding直接输出error,不输出已解码的字符~HuffMan(); //回收HuffTree空间
};
//以下完成Huffman类的定义填空
HuffMan::~HuffMan() {if (HuffTree) delete[]HuffTree;len = lnum = 0;
}void HuffMan::selectMin(int n,int &x1,int &x2) {x1 = x2 = 0;for (int i = 1; i <= n; i++) {if (HuffTree[i].parent == 0) {if (x1 == 0) x1 = i;else if (x2 == 0)x2 = i;if (HuffTree[i].weight < HuffTree[x1].weight) {x2 = x1; x1 = i;}else if (x2 != 0 && HuffTree[i].weight < HuffTree[x2].weight)x2 = i;}}
}HuffMan::HuffMan(int n,int w[],char c[]) {lnum = n;len = 2 * n - 1;HuffTree = new HuffNode[len + 1];for (int i = 1; i <= len; i++) {HuffTree[i].weight = 0;HuffTree[i].lchild = 0;HuffTree[i].rchild = 0;HuffTree[i].letter = 0;HuffTree[i].parent = 0;}for (int i = 1; i <= lnum; i++) {HuffTree[i].weight = w[i - 1];HuffTree[i].letter = c[i - 1];}
}
void HuffMan::buildTree() {int x1, x2;for (int i = lnum + 1; i <= len; i++) {selectMin(i - 1, x1, x2);HuffTree[x1].parent = i;HuffTree[x2].parent = i;HuffTree[i].lchild = x1;HuffTree[i].rchild = x2;HuffTree[i].weight = HuffTree[x1].weight + HuffTree[x2].weight;}
}void HuffMan::Decoding(string cs) {string decode;int k = len;for (int i = 0; i < cs.length(); i++) {if (cs[i] == '0') {if (HuffTree[k].lchild)k = HuffTree[k].lchild;else {cout << "error" << endl;return;}}else {if (HuffTree[k].rchild)k = HuffTree[k].rchild;else {cout << "error" << endl;return;}}if (HuffTree[k].lchild == 0 && HuffTree[k].rchild == 0) {decode += HuffTree[k].letter;k = len;}}if (k == len) cout << decode << endl;else cout << "error" << endl;
}
int main()
{ int i, n, wt[100];char ct[100];string cstr;cin>>n;for(i=0;i<n;i++)cin>>wt[i];for(i=0;i<n;i++)cin>>ct[i];HuffMan huff(n,wt, ct);huff.buildTree(); //构建赫夫曼树cin>>i;while (i--){ cin>>cstr;huff.Decoding(cstr); //赫夫曼解码}return 0;
}C. DS树--带权路径和
题目描述
计算一棵二叉树的带权路径总和,即求赫夫曼树的带权路径和。
已知一棵二叉树的叶子权值,该二叉树的带权案路径和APL等于叶子权值乘于根节点到叶子的分支数,然后求总和。如下图中,叶子都用大写字母表示,权值对应为:A-7,B-6,C-2,D-3
树的带权路径和 = 7*1 + 6*2 + 2*3 + 3*3 = 34
本题二叉树的创建参考前面的方法
输入
第一行输入一个整数t,表示有t个二叉树
第二行输入一棵二叉树的先序遍历结果,空树用字符‘0’表示,注意输入全是英文字母和0,其中大写字母表示叶子
第三行先输入n表示有n个叶子,接着输入n个数据表示n个叶子的权值,权值的顺序和前面输入的大写字母顺序对应
以此类推输入下一棵二叉树
输出
输出每一棵二叉树的带权路径和
输入:
2
xA00tB00zC00D00
4 7 6 2 3
ab0C00D00
2 10 20输出:
34
40#include <iostream>
#include <string>
using namespace std;
class BiTreeNode {
public:char data; //数据域BiTreeNode* leftChild, * rightChild; //左右子树指针BiTreeNode() :leftChild(NULL), rightChild(NULL) {}~BiTreeNode() {}
};class BiTree {
private:BiTreeNode* root; //根结点指针string sTree; //建树字符串int pos,sum=0; //标识建树字符串的当前字符位置int* arry;int j = 0;//路径数组下标int road[100];int high=0;BiTreeNode* CreateTree();//建树私有函数void PreOrder(BiTreeNode* t); //先序遍历实现void InOrder(BiTreeNode* t); //中序遍历实现void PostOrder(BiTreeNode* t); //后序遍历实现void findroad(BiTreeNode* t);
public:BiTree() :root(NULL) {};void Create(string vArray,int arr[],int n); //建树公有接口,参数是特定的先序遍历字符串void PreOrder(); //先序遍历公有接口void InOrder(); //中序遍历公有接口void PostOrder(); //后序遍历公有接口void findroad();void calculate();
};
//二叉树公有接口的实现
void BiTree::Create(string vArray,int arr[],int n)
{pos = 0;sTree.assign(vArray); //把参数保存到内部字符串root = CreateTree(); //建树成功后root指向根结点arry = new int[n];for (int i = 0; i < n; i++)arry[i] = arr[i];/*for (int i = 0; i < n; i++)cout << arry[i];*/
}
void BiTree::PreOrder()
{PreOrder(root);
}
void BiTree::InOrder()
{InOrder(root);
}
void BiTree::PostOrder()
{PostOrder(root);
}
void BiTree::findroad()
{findroad(root);
}
//请完成上述类内部的私有函数实现
BiTreeNode* BiTree::CreateTree()
{BiTreeNode* node;int l = sTree.length();if (sTree[pos] != '0'){node = new BiTreeNode;node->data = sTree[pos];pos++;node->leftChild = CreateTree();node->rightChild = CreateTree();}else{pos++;node = NULL;}return node;
}
void BiTree::PreOrder(BiTreeNode* t)
{if (t == NULL)return;cout << t->data;PreOrder(t->leftChild);PreOrder(t->rightChild);}
void BiTree::InOrder(BiTreeNode* t)
{if (t == NULL)return;InOrder(t->leftChild);cout << t->data;InOrder(t->rightChild);
}
void BiTree::PostOrder(BiTreeNode* t)
{if (t == NULL)return;PostOrder(t->leftChild);PostOrder(t->rightChild);cout << t->data;
}
void BiTree::findroad(BiTreeNode* t)
{if (t!=NULL){if (t->leftChild==NULL && t->rightChild==NULL){road[j] = high;j++;}else{if (t->leftChild != NULL){high++;findroad(t->leftChild);}if (t->rightChild != NULL){high++;findroad(t->rightChild);}}high--;}
}
void BiTree::calculate()
{/*cout << j << endl;*/for (int i = 0; i < j; i++){sum += arry[i] * road[i];}cout << sum << endl;
}//主函数
int main()
{int t;string vArray;cin >> t;while (t--){cin >> vArray;BiTree myTree;int n;cin >> n;int* a = new int[n];for (int i = 0; i < n; i++){cin >> a[i];}myTree.Create(vArray,a,n);myTree.findroad();myTree.calculate();/*myTree.PreOrder(); cout << endl;*//*myTree.InOrder(); cout << endl;myTree.PostOrder(); cout << endl;*/delete[]a;}return 0;
}D. DS树--二叉树之最大路径
题目描述
给定一颗二叉树的逻辑结构(先序遍历的结果,空树用字符‘0’表示,例如AB0C00D00),建立该二叉树的二叉链式存储结构
二叉树的每个结点都有一个权值,从根结点到每个叶子结点将形成一条路径,每条路径的权值等于路径上所有结点的权值和。编程求出二叉树的最大路径权值。如下图所示,共有4个叶子即有4条路径,
路径1权值=5 + 4 + 11 + 7 = 27路径2权值=5 + 4 + 11 + 2 = 22
路径3权值=5 + 8 + 13 = 26路径4权值=5 + 8 + 4 + 1 = 18
可计算出最大路径权值是27。
该树输入的先序遍历结果为ABCD00E000FG00H0I00,各结点权值为:
A-5,B-4,C-11,D-7,E-2,F-8,G-13,H-4,I-1
输入
第一行输入一个整数t,表示有t个测试数据
第二行输入一棵二叉树的先序遍历,每个结点用字母表示
第三行先输入n表示二叉树的结点数量,然后输入每个结点的权值,权值顺序与前面结点输入顺序对应
以此类推输入下一棵二叉树
输出
每行输出每棵二叉树的最大路径权值,如果最大路径权值有重复,只输出1个
输入:
2
AB0C00D00
4 5 3 2 6
ABCD00E000FG00H0I00
9 5 4 11 7 2 8 13 4 1输出:
11
27代码:
#include <iostream>
#include<queue>
using namespace std;class HTNode
{
private:char data;int weight;HTNode* lchild, * rchild;
public:HTNode() :weight(0), lchild(NULL), rchild(NULL) {}~HTNode() {}friend class HuffmanTree;
};class HuffmanTree
{
private:HTNode* root;int LeafNum;int Maxroad;queue<int> weights;
public:~HuffmanTree();void CreateTree();void CreateTree(HTNode*& p, int& i, int& j);void getRoad();void getRoad(HTNode* p, int Level);
};HuffmanTree::~HuffmanTree()
{delete root;}void HuffmanTree::CreateTree(HTNode*& p, int& i, int& j)
{char c;cin >> c;if (c == '0') { p = NULL;}else {p = new HTNode;p->data = c;CreateTree(p->lchild, i, j);CreateTree(p->rchild, i, j);}}void HuffmanTree::CreateTree()
{int i = 0;int j = 0;CreateTree(root, i, j);
}void HuffmanTree::getRoad(HTNode* t, int road)
{if (t){ t->weight = weights.front() + road;weights.pop();getRoad(t->lchild, t->weight);getRoad(t->rchild, t->weight);if (!t->lchild && !t->rchild)if (t->weight > Maxroad)Maxroad = t->weight;}}
void HuffmanTree::getRoad() {int n;cin >> n;Maxroad=0;while (n--){int e;cin >> e;weights.push(e);}getRoad(root, 0);cout << Maxroad<<endl ;}int main(void)
{int t;cin >> t;while (t--){HuffmanTree myTree;myTree.CreateTree();myTree.getRoad();}return 0;
}E. DS二叉树—二叉树镜面反转
题目描述
假设二叉树用二叉链表存储,用先序序列结果创建。输入二叉树的先序序列,请你先创建二叉树,并对树做个镜面反转,再输出反转后的二叉树的先序遍历、中序遍历、后序遍历和层序遍历的序列。所谓镜面反转,是指将所有非叶结点的左右孩子对换。
--程序要求--
程序中不允许使用STL库等第三方对象或函数实现本题的要求
输入
测试次数t
每组测试数据是一个二叉树的先序遍历序列,#表示空树
输出
对每棵二叉树,输出镜面反转后的先序、中序、后序和层次遍历序列。如果空树,输出四个NULL(后面不加空格,每个NULL独自一行,中间没有空行)。如下:
NULL
NULL
NULL
NULL
输入:
3
41#32###65##7##
AB#C##D##
AB##C##输出:
4 6 7 5 1 3 2
7 6 5 4 3 2 1
7 5 6 2 3 1 4
4 6 1 7 5 3 2
A D B C
D A C B
D C B A
A D B C
A C B
C A B
C B A
A C B 代码:
#include<iostream>
using namespace std;
class node {
public:char data;node* left, * right;node() { left = right = NULL; }~node(){}
};
class tree {node* root;int pos;string str;node* createtree();void preOrder(node* root);void inOrder(node* root);void postOrder(node* root);void levelOrder(node* root);void exchange(node* root);
public:void create(string s);void inOrder();void preOrder();void postOrder();void exchange();void levelOrder();
};
void tree::exchange() {if (root != NULL) {exchange(root);}
}
void tree::exchange(node* root) {if (root != NULL) {exchange(root->left);exchange(root->right);node* p = new node();p = root->left;root->left = root->right;root->right = p;}
}
void tree::create(string s) {pos = 0;str = s;root = createtree();
}
node* tree::createtree() {node* p = new node();char c = str[pos++];if (c == '#') p = NULL;else {p->data = c;p->left = createtree();p->right = createtree();}return p;
}
void tree::preOrder() {if (str[0] == '#') cout << "NULL";else preOrder(root);cout << endl;
}
void tree::preOrder(node* root) {if (root) {cout << root->data << ' ';preOrder(root->left);preOrder(root->right);}
}
void tree::inOrder() {if (str[0] == '#') cout << "NULL";else inOrder(root);cout << endl;
}
void tree::inOrder(node* root) {if (root) {inOrder(root->left);cout << root->data << ' ';inOrder(root->right);}
}
void tree::postOrder() {if (str[0] == '#') cout << "NULL";else postOrder(root);cout << endl;
}
void tree::postOrder(node* root) {if (root) {postOrder(root->left);postOrder(root->right);cout << root->data << ' ';}
}
void tree::levelOrder() {if (str[0] == '#') cout << "NULL";else levelOrder(root);cout << endl;
}
void tree::levelOrder(node* root) {//不给用STL,有点大病)node** que = new node*[100];for (int i = 0; i < 100; i++) que[i] = new node();int front = 0, rear = 0,temp=0;node* p = root;que[temp++] = p; rear++;while (1) {p = que[front];front++;cout << p->data << " ";if (p->left) {que[temp++] = p->left; rear++;}if (p->right) {que[temp++] = p->right; rear++;}if (front == rear) break;}
}
int main() {int t; cin >> t;string s;while (t--) {cin >> s;tree t;t.create(s);t.exchange();t.preOrder();t.inOrder();t.postOrder();t.levelOrder();}
}相关文章:
)
实验07 赫夫曼编码及综合2022(带程序填空)
A. 【程序填空】赫夫曼编码题目描述给定n个叶子的权值,根据这些权值构造huffman树,并输出huffman编码参考课本第6.6节的算法6.12,注意算法中数组访问是从位置1开始赫夫曼构建中,默认左孩子权值不大于右孩子权值如果遇到两个孩子权…...
分布式 CAP BASE理论
文章目录CAP简介不是所谓的“3 选 2”CAP 实际应用案例BASE简介BASE 理论的核心思想总结CAP 简介 在理论计算机科学中,CAP 定理(CAP theorem)指出对于一个分布式系统来说,当设计读写操作时,只能同时满足以下三点中的…...

三调地类筛选器,Arcgis地类筛选
三调地类在使用是,需要分类统计,这个可以用于筛选; 标准地类筛选 农用地: DLBM IN(0303,0304,0306,0402,0101,0102,0103,0201,0201K,0202,0202K,0203,0203K,0204,0204K,0301,0301K,0302,0302K,0305,0307,0307K,0401,0403,0403K…...
)
华为OD机试 - 密室逃生游戏(Python)
密室逃生游戏 题目 小强增在参加《密室逃生》游戏,当前关卡要求找到符合给定 密码 K(升序的不重复小写字母组成) 的箱子, 并给出箱子编号,箱子编号为 1~N 。 每个箱子中都有一个 字符串 s ,字符串由大写字母、小写字母、数字、标点符号、空格组成, 需要在这些字符串中…...

白话C#之委托
一、什么是委托? 书本上是这样来定义委托的: 委托是一种动态调用方法的类型,属于引用型。委托是对方法的抽象和封装。委托对象实质上代表了方法的引用(即内存地址)。委托通常是委托某个方法来实现具体的功能。当我们调…...
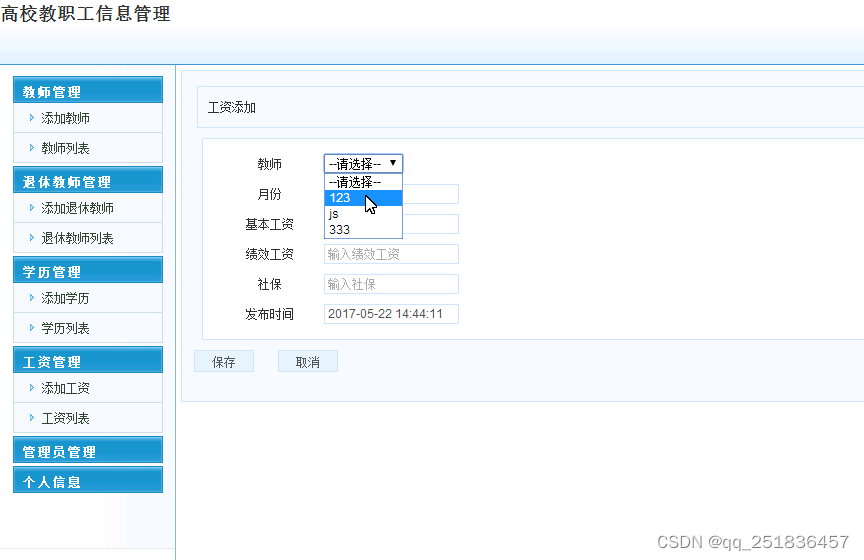
jsp高校教职工管理系统Myeclipse开发mysql数据库web结构java编程计算机网页项目
一、源码特点 jsp 高校教职工管理系统 是一套完善的web设计系统,对理解JSP java编程开发语言有帮助mvc模式 serlvetdaobean方式开发,系统具有完整的源代码和数据库,系统主要采用B/S模式 开发。开发环境为TOMCAT7.0,Myeclipse8.5开发&#…...

2023年数学建模美赛A题(A drought stricken plant communities)分析与编程
2023年数学建模美赛A题(A drought stricken plant communities)分析与编程 2023年数学建模美赛D题(Prioritizing the UN Sustainability Goals)分析与编程 特别提示: 1 本文介绍2023年美赛题目,进行深入分析…...

Delphi 中自定义鼠标指针图像
Dephi中的鼠标指针是可以自由定义的,如果是使用系统提供的图标,那么直接通过可视控件的Cursor属性赋值就可以。例如设置Form的鼠标为 crHourGlass 沙漏:Form1.Cursor : crHourGlass;也可以在设计期(IDE环境中)直接更改…...

【计算机网络】物理层
文章目录物理层的基本概念传输媒体同轴电缆双绞线光纤电力线电磁波红外线可见光传输方式串行传输和并行传输同步传输和异步传输单工,半双工以及全双工通信编码与调制常用编码不归零编码归零编码曼彻斯特编码差分曼彻斯特编码基本调制混合调制信道的极限容量奈氏准…...
)
华为OD机试 - 最少停车数(Python)
最少停车数 题目 特定大小的停车场 数组cars表示 其中1表示有车0表示没车 车辆大小不一,小车占一个车位(长度1) 货车占两个车位(长度2) 卡车占三个车位(长度3) 统计停车场最少可以停多少辆车 返回具体的数目 输入 整型字符串数组cars 其中1表示有车0表示没车 数组长度 <…...
)
面试题-前端开发JavaScript篇上(答案超详细)
文章目录 闭包说一下类的创建和继承如何解决异步回调地狱说说前端中的事件流如何让事件先冒泡后捕获说一下事件委托说一下图片的懒加载和预加载mouseover 和 mouseenter 的区别JS 的 new 操作符做了哪些事改变函数内部 this 指针的指向函数(bind,apply,call 的区别)JS 的各种…...

【计算机网络】运输层
文章目录运输层概述运输层端口号、复用与分用的概念UDP和TCP的对比TCP的流量控制TCP的拥塞控制TCP超时重传时间的选择TCP可靠传输的实现TCP的运输连接管理TCP的连接建立(3次握手)TCP的连接释放(4次挥手)TCP报文段的首部格式运输层概述 这里我们对运输层进行概述,之…...
)
20222023华为OD机试 - 基站维修工程师(Python)
基站维修工程师 题目 小王是一名基站维护工程师,负责某区域的基站维护。 某地方有 n 个基站( 1<n<10 ),已知各基站之间的距离 s( 0<s<500 ), 并且基站 x 到基站 y 的距离,与基站 y 到 基站 x 的距离并不一定会相同。 小王从基站 1 出发,途经每个基站 1 …...
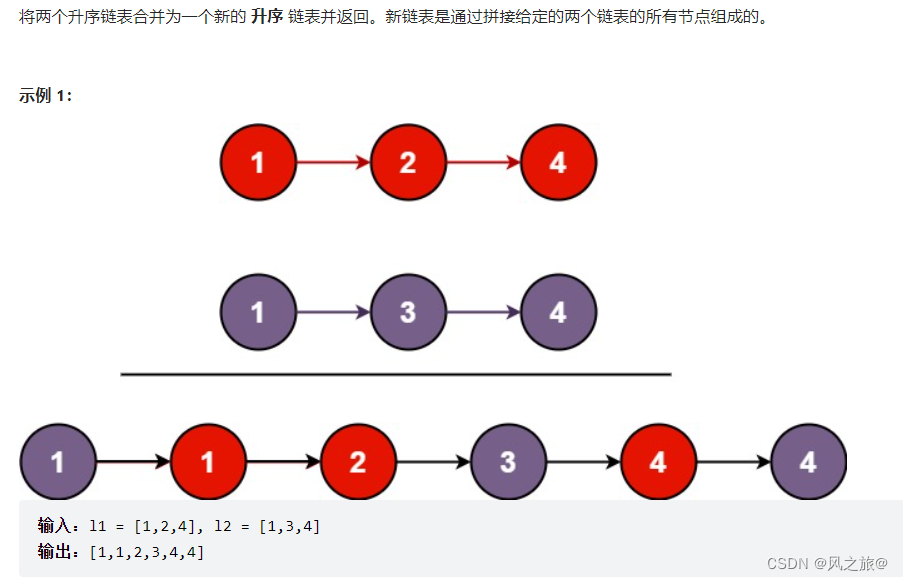
21. 合并两个有序链表
题目链接:解题思路:遍历,双指针:因为两个链表有序,所以只需要依次比较两个元素的大小,然后添加到新的链表中即可first指针指向第一个链表l1,second指针指向第二个链表l2,answer保存合…...

产品经理知识体系:5.如何做好产品数据分析?
数据分析 思考 笔记 数据分析 思路 基于用户路径:用户的活动路径,操作流程等行为数据。 基于产品节点:转化率、占比 分析类型 先定性:先抛出问题、提出假设 再定量:数据验证问题、验证假设 先定性、再定量、最后得…...

详解垃圾回收算法,优缺点是什么?|金三银四系列
本文详细介绍了在 JVM 中如何判断哪些对象是需要回收的,以及不同的垃圾回收算法以及优缺点。点击上方“后端开发技术”,选择“设为星标” ,优质资源及时送达上篇文章详细介绍了 JVM 的结构以及其内存结构,需要阅读请移步。本文主要…...
 SnapshotManager 之标识文件)
Android 虚拟 A/B 详解(七) SnapshotManager 之标识文件
本文为洛奇看世界(guyongqiangx)原创,转载请注明出处。 原文链接:https://blog.csdn.net/guyongqiangx/article/details/129098176 Android 虚拟 A/B 分区《Android 虚拟 A/B 分区》系列,更新中,文章列表: Android 虚拟 A/B 详解(一) 参考资料推荐Android 虚拟 A/B 详解(二…...

LA@生成子空间@范数@衡量矩阵大小@正交化
文章目录线性组合与线性方程组生成子空间范数LpL^pLp范数向量点积用范数表示ref衡量矩阵大小特殊类型矩阵和向量对角阵向量长度性质单位向量向量单位化(正规化)正交向量正交正交向量组标准正交基正交化(schmidt)正交矩阵矩阵是正交矩阵的充要条件对称矩阵正交相似概念区分&…...

MT2012_竹鼠的白色季节
竹鼠的白色季节 #include<bits/stdc.h> #include<algorithm> using namespace std;/*思路:从小到大排序,然后依次往后遍历即可*/ int main( ) {int n,d;cin>>n>>d; int tmp;vector<int>nums;for(int i0;i<n;i){cin&…...

MySQL是什么?它有什么优势?
随着时间的推移,开源数据库在中低端应用中逐渐流行起来,占据了很大的市场份额。开源数据库具有免费使用、配置简单、稳定性好、性能优良等特点,而 MySQL 数据库正是开源数据库中的杰出代表。 开源全称为“开放源代码”。很多人认为开源软件最…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

Neko虚拟浏览器远程协作方案:Docker+内网穿透技术部署实践
前言:本文将向开发者介绍一款创新性协作工具——Neko虚拟浏览器。在数字化协作场景中,跨地域的团队常需面对实时共享屏幕、协同编辑文档等需求。通过本指南,你将掌握在Ubuntu系统中使用容器化技术部署该工具的具体方案,并结合内网…...

倒装芯片凸点成型工艺
UBM(Under Bump Metallization)与Bump(焊球)形成工艺流程。我们可以将整张流程图分为三大阶段来理解: 🔧 一、UBM(Under Bump Metallization)工艺流程(黄色区域ÿ…...
