卡尔曼滤波算法demo
代码
learn_kalman.py
#coding=utf-8
import numpy as np
import time
from kinematic_model import freedrop
from controller import kalman_filterimport matplotlib.pyplot as plt
# 支持中文
import matplotlib as mpl
mpl.rcParams['font.family']='SimHei'
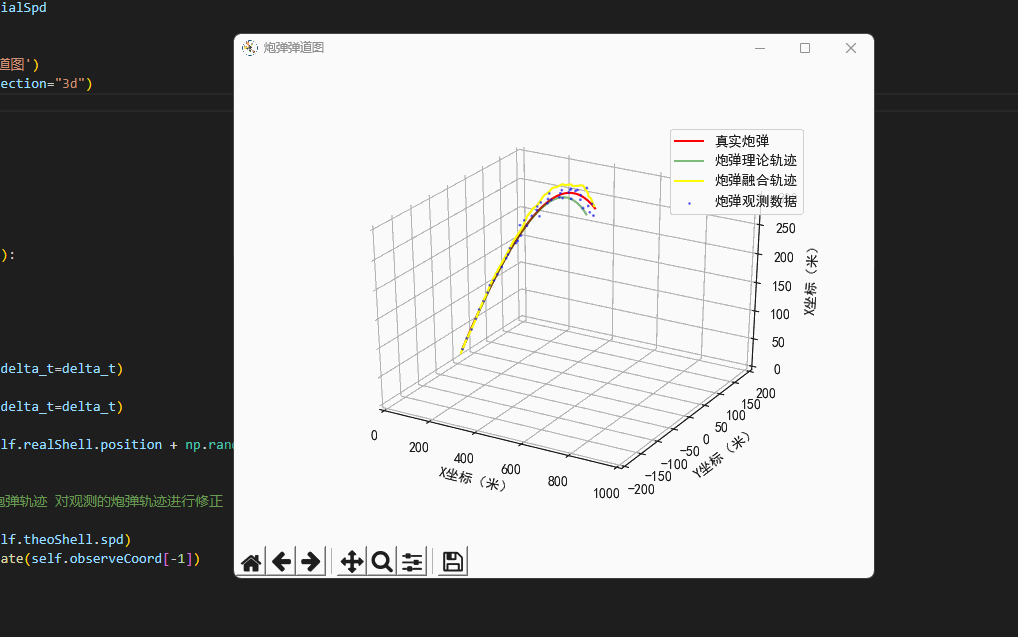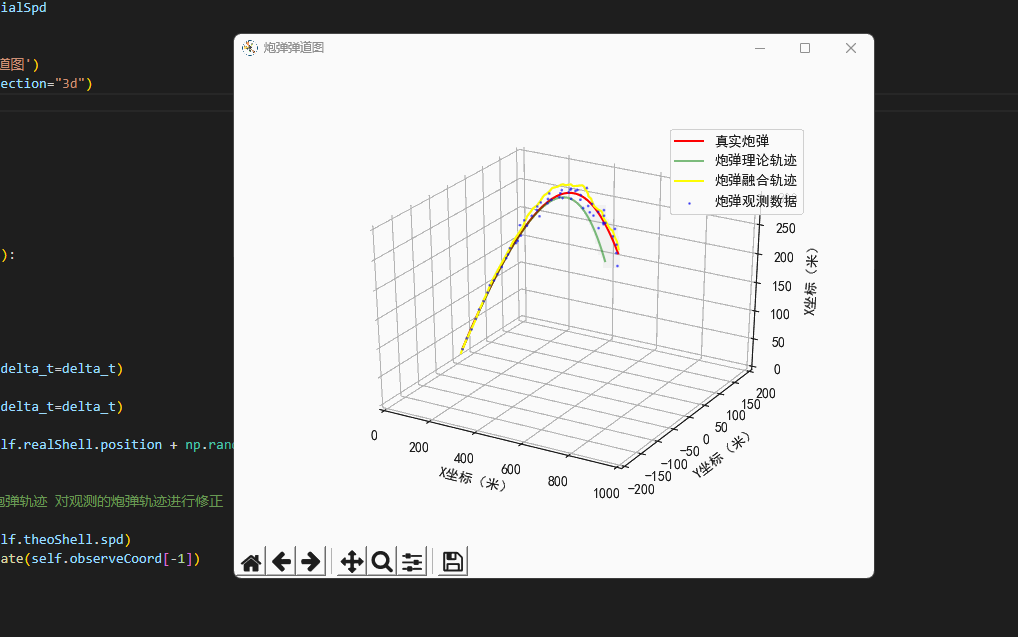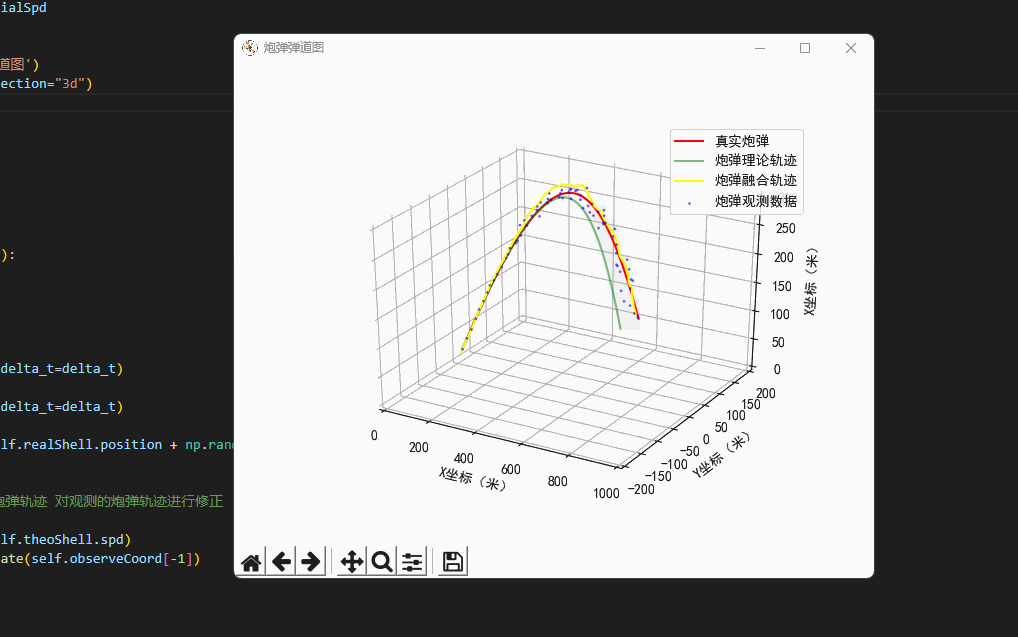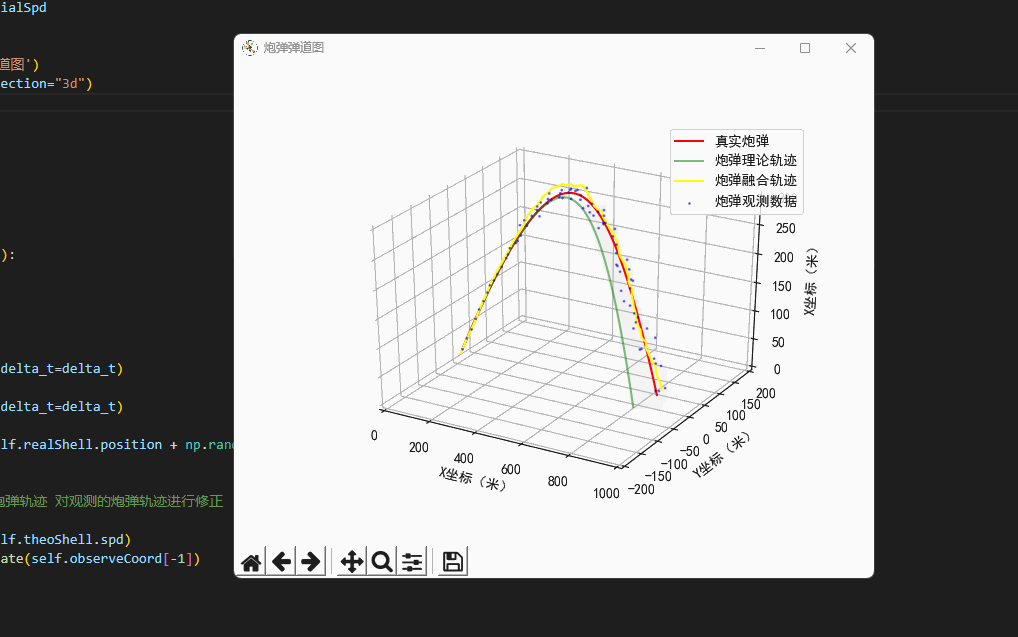
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号class Scene:'''场景'''def __init__(self,windSpd=np.array([0.7,0.3,0.0]),\initialSpd=np.array([120.0,0.0,120.0])):'''我现在是一个防空兵防空炮打出一枚炮弹,真实的炮弹轨迹,它可能会受风的影响,可能会有随机因素导致偏离目标导致打不中飞机...我们可以使用指挥所观测到的炮弹轨迹,因为炮弹距离很远,所以这个观测不是很靠谱...所以我们所使用了卡尔曼滤波算法,得到了一条真实的炮弹轨迹...'''# 真实的炮弹self.realShell=freedrop.FreeDropBinder(windSpd=windSpd,initialSpd=initialSpd)# 理论上炮弹的落点self.theoShell=freedrop.FreeDropBinder(windSpd=np.array([0.0,0.0,0.0]),initialSpd=initialSpd,randRatio=0.0)# 卡卡尔曼滤波器self.kf=kalman_filter.KF_Onmi3D()self.kf.initState[3:6]=initialSpd# 绘图区self.fig=plt.figure('炮弹弹道图')self.ax = self.fig.gca(projection="3d")# 数据缓存self.realCoord=[]self.theoCoord=[]self.kalmanCoord=[]self.observeCoord=[]def UpdateData(self,delta_t=0.2):'''更新虚拟环境的数据:return:'''# 真实炮弹轨迹self.realShell.StateUpdate(delta_t=delta_t)# 理论炮弹轨迹self.theoShell.StateUpdate(delta_t=delta_t)# 观测到的炮弹轨迹self.observeCoord.append(self.realShell.position + np.random.random(3) * self.realShell.position[0]/20.0 - self.realShell.position[0]/40.0)# 卡尔曼滤波'''基于卡尔曼滤波,结合理论炮弹轨迹 对观测的炮弹轨迹进行修正'''self.kf.Predict(velocity=self.theoShell.spd)Hybrid_Position=self.kf.Update(self.observeCoord[-1])# 绘图(真实的弹道)plt.cla()self.ax.set_xlim(0, 1000)self.ax.set_ylim(-200, 200)self.ax.set_zlim(0, 300)self.ax.set_xlabel("X坐标(米)")self.ax.set_ylabel("Y坐标(米)")self.ax.set_zlabel("X坐标(米)")# 计算三个类型的炮弹self.realCoord.append(np.copy(self.realShell.position)) # 真实炮弹self.theoCoord.append(np.copy(self.theoShell.position)) # 理论模型self.kalmanCoord.append(np.copy(Hybrid_Position))self.curve2Draw=np.array(self.realCoord)self.curve2 = np.array(self.observeCoord)self.curve3 = np.array(self.theoCoord)self.curve4 = np.array(self.kalmanCoord)self.ax.plot(self.curve2Draw[:,0],self.curve2Draw[:,1],self.curve2Draw[:,2],label='真实炮弹',color='red')self.ax.scatter(self.curve2[:, 0], self.curve2[:, 1], self.curve2[:, 2],'rv+', label='炮弹观测数据', color='blue',alpha=0.5,s=1)self.ax.plot(self.curve3[:, 0], self.curve3[:, 1], self.curve3[:, 2], label='炮弹理论轨迹', color='green', alpha=0.5)self.ax.plot(self.curve4[:, 0], self.curve4[:, 1], self.curve4[:, 2], label='炮弹融合轨迹', color='yellow', alpha=1.0)self.ax.legend()plt.pause(0.05)# 开始模拟环境
#plt.ion()s=Scene()for i in range(1000):if s.realShell.position[2]<0: breaks.UpdateData()
plt.ioff()
plt.show()freerop.py
#coding=utf-8
import timeimport numpy as np
'''3D自由落体模型(含有风阻)
'''class FreeDropBinder:'''为实体绑定自由落体属性'''def __init__(self,windSpd=np.array([0.0,0.0,0.0]),resRatio=0.0004,G=9.8,initialPos=np.array([0.0,0.0,0.0]),initialSpd=np.array([0.0,0.0,0.0]),randRatio=0.1):''':param windSpd: 风速(三维):param resRatio: 风阻比例(全向):param G: 重力加速度:param initialPos: 物体初始位置:param initialSpd: 物体初始速度'''self.position=initialPosself.spd=initialSpdself.windSpd=windSpdself.resRatio=resRatioself.G=Gself.randRatio=randRatiodef StateUpdate(self,delta_t=0.05,driveForce=np.array([0.0,0.0,0.0])):'''更新实体位置信息:param delta_t::return:'''# 重力因素self.spd+=np.array([0,0,-self.G*delta_t])# 风阻因素self.spd=np.where(self.spd>0,self.spd-self.resRatio*self.spd*self.spd,self.spd)self.spd = np.where(self.spd <= 0, self.spd + self.resRatio * self.spd * self.spd, self.spd)# 风力因素# 驱动因素self.spd+=(driveForce+self.windSpd)*delta_t# 随机因素self.spd+=(np.random.rand(3)-0.5)*2*self.randRatio*delta_t# 更新坐标self.position=self.position+self.spd*delta_tif __name__=='__main__':box=FreeDropBinder(initialSpd=np.array([10.0,0.0,100.0]))for i in range(30):print(box.Update())
kalman_filter.py
import numpy as np
import matplotlib.pyplot as pltclass KF_Onmi3D:'''三维,无方向场景下的卡尔曼滤波算法模组'''def __init__(self):# 初始状态 x y z vx vy vzself.initState=np.array([0, 0, 0, 0, 0, 0],dtype=np.float)# 初始协方差,可以看出是每个维度都是一一对应的关系'''[ 1 0 0 0 0 0 ][ 0 1 0 0 0 0 ][ 0 0 1 0 0 0 ][ 0 0 0 1 0 0 ][ 0 0 0 0 1 0 ][ 0 0 0 0 0 1 ]'''self.initCov=np.eye(6)# 状态转移矩阵self.stateTransMatrix=np.array([[1,0,0,1,0,0],[0,1,0,0,1,0],[0,0,1,0,0,1],[0,0,0,1,0,0],[0,0,0,0,1,0],[0,0,0,0,0,1]],dtype=np.float)# 观测矩阵 X Y Z Vx Vy Vzself.observeMatrix=np.array([[1, 0, 0, 0, 0, 0],[0, 1, 0, 0, 0, 0],[0, 0, 1, 0, 0, 0]],dtype=np.float)# 过程噪声(先设定一个初始值,这个需要跟据你系统的评估来确定)self.procNoise=np.eye(6)*0.001# 观测噪声的协方差矩阵self.observeNoiseCov=np.eye(3)*1self.InitParams()def InitParams(self):'''初始化状态变量:return:'''self.currentState=self.initState.copy()self.predictState=self.initState.copy()self.currentCov=self.initCovself.predictedCov=self.currentCovdef Predict(self,velocity=np.array([0,0,0],dtype=np.float)):'''预测过程:param v::return:'''# 基于当前的速度,预测机器人下一个状态的状态数值self.predictState=self.stateTransMatrix.dot(self.currentState)# 预测三维环境下的协方差矩阵self.predictedCov=self.stateTransMatrix.dot(self.currentCov).dot(self.stateTransMatrix.T)+self.procNoise# 把速度赋值给状态中的“速度”属性self.currentState[3:6] = velocitydef Update(self,observed_Pos=np.array([0,0,0],dtype=np.float)):'''更新数据:param observed_Pos: 带有误差的位置观测值:return:'''# 卡尔曼增益(Kalman Gain)计算'''K=\frac{估计的误差}{估计的误差+测量的误差}=\frac{\hat{P_k}C}{C\hat{P_k}C^T+Error}'''self.Kalman_Gain = self.predictedCov.dot(self.observeMatrix.T) \.dot(np.linalg.inv( \self.observeMatrix.dot(self.predictedCov).dot(self.observeMatrix.T) + self.observeNoiseCov))'''基于Kalman Gain估算当前状态'''self.currentState = self.predictState + self.Kalman_Gain.dot(observed_Pos-self.observeMatrix.dot(self.predictState))'''当前协方差估计'''self.currentCov = (np.eye(6) - self.Kalman_Gain.dot(self.observeMatrix)).dot(self.predictedCov)return self.currentState[0:3]
参考
https://www.bilibili.com/video/BV1gF411f78t/?spm_id_from=333.337.top_right_bar_window_history.content.click&vd_source=667c3d14dbb51ec849c0bc7c38329d10
相关文章:

卡尔曼滤波算法demo
代码 learn_kalman.py #codingutf-8 import numpy as np import time from kinematic_model import freedrop from controller import kalman_filterimport matplotlib.pyplot as plt # 支持中文 import matplotlib as mpl mpl.rcParams[font.family]SimHei plt.rcParams[a…...
MySQL游标(二十九)
二八佳人体似酥,腰悬利剑斩愚夫,虽然不见人头落,暗里教君骨髓枯。 上一章简单介绍了MySQL流程控制(二十八) ,如果没有看过,请观看上一章 一. 游标 一.一 什么是游标 虽然我们也可以通过筛选条件 WHERE 和 HAVING,或者是限定返回记录的关键…...
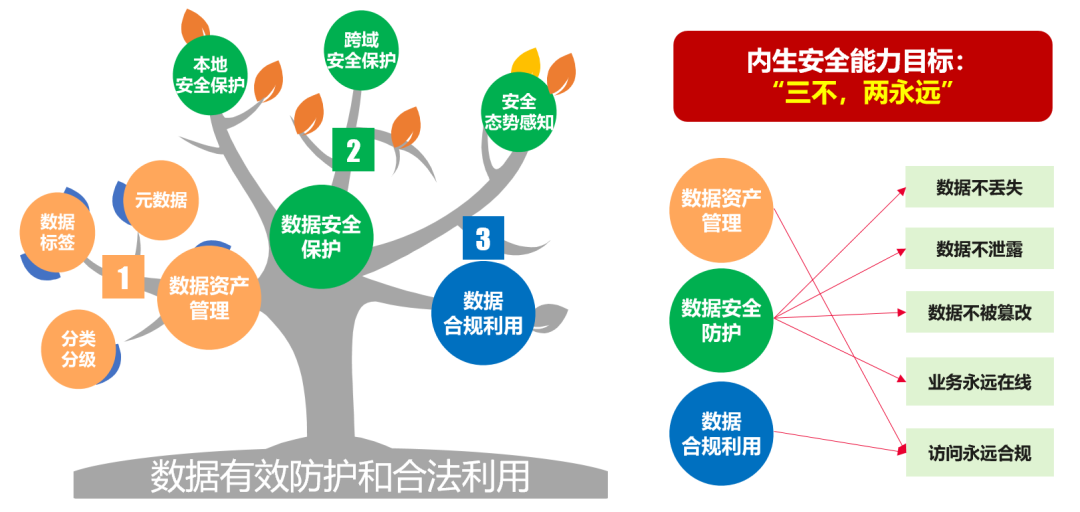
内生安全构建数据存储
一、数据安全成为防护核心,存储安全防护不容有失 1、数据作为企业的核心资产亟需重点保护,数据安全已成网络空间防护核心 2、国家高度重视关键信息基础设施的数据安全,存储安全已成为审核重点 二、存储安全是数据安全的关键一环,应…...
Docker+Consul+Registrator 实现服务注册与发现
第四阶段 时 间:2023年8月8日 参加人:全班人员 内 容: DockerConsulRegistrator 实现服务注册与发现 目录 一、服务注册中心引言 CAP理论是分布式架构中重要理论: 二、服务注册中心软件 (一)Zoo…...
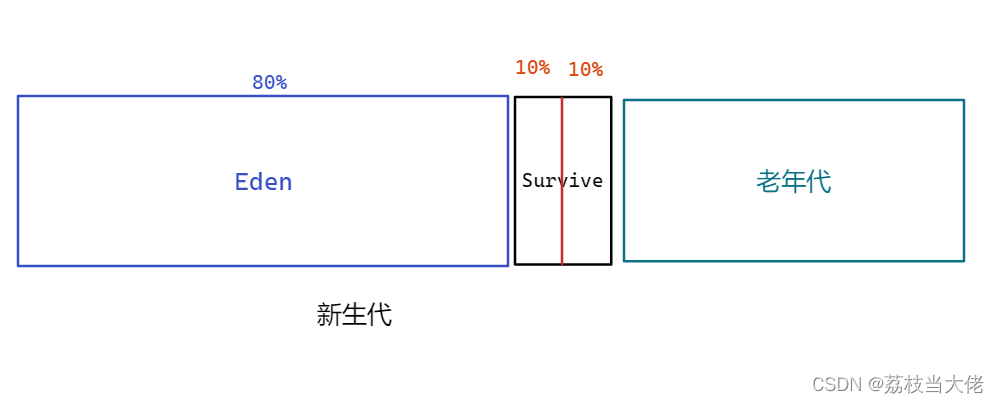
深入学习JVM —— GC垃圾回收机制
前言 前面荔枝已经梳理了有关JVM的体系结构和类加载机制,也详细地介绍了JVM在类加载时的双亲委派模型,而在这篇文章中荔枝将会比较详细地梳理有关JVM学习的另一大重点——GC垃圾回收机制的相关知识,重点了解的比如对象可达性的判断、四种回收…...
)
Centos7.6 + Apache Ranger 2.4.0编译(docker方式)
目录 一、Ranger简介 1、组件列表 2、支持的数据引擎服务 二、主机环境准备 1、关闭防火墙 2、关闭SELINUX 3、安装docker 4、下载Ranger源码包 5、下载Maven安装包 三、编译Ranger源码 1、修改官方包中的build_ranger_using_docker.sh 2、运行脚本编译 3、编译检…...

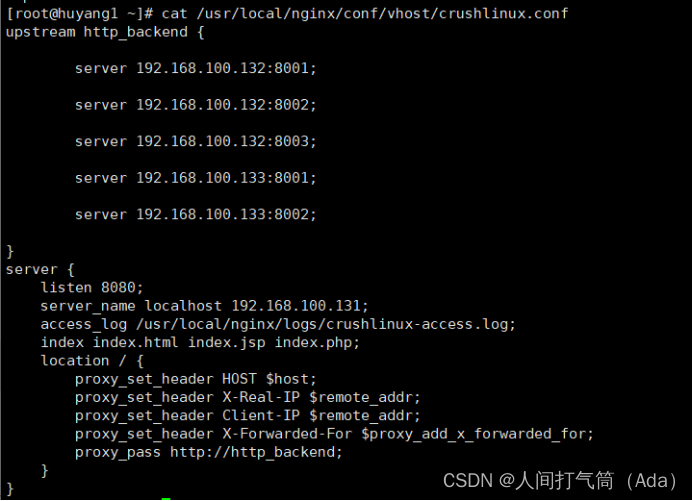
LVS-DR模式集群配置
四台虚拟机 node1:128 node2:135 RS端: node3:130 node4:132 [rootnode2 ~]# yum install -y ipvsadm #配置LVS虚拟IP,没有ifconfig命令则先安装 [rootnode2 ~]# yum install net-tools -y #配置VIP [root…...
)
【数据分析】pandas( 二)
目录 简介: 一,1.1来自Series字典或字典 1.2 来自ndarray或者列表的字典: 1.3来自结构化或记录数组; 1.4来自字典列表: 1.4来自元组的字典: 1.5 来自Series 二,代替构造函数: 2.1DataFram…...
ffmpeg工具实用命令
说明:ffmpeg是一款非常好用的媒体操作工具,包含了许多对于视频、音频的操作,有些视频播放器里面实际上就是使用了ffmpeg。本文介绍ffmpeg的使用以及一些较为实用的命令。 安装 ffmpeg是命令行操作的,不需要安装,可在…...

zabbix API笔记
博客园原文 python简单demo 输出id为111主机的主机群组信息 import requests import json request_headers {"Content-Type": "application/json"} zabbix_url "http://xxx.xxx.xxx.xxx:8080/zabbix/api_jsonrpc.php" get_hostgroup_from_h…...

[HDLBits] Mt2015 q4a
Module A is supposed to implement the function z (x^y) & x. Implement this module. module top_module (input x, input y, output z);assign z(x^y)&x; endmodule...
HarmonyOS NEXT,生命之树初长成
在不同的神话体系中,都有着关于生命之树的记载。 比如在北欧神话中,一株巨大的树木联结着九大世界,其被称为“尤克特拉希尔”Yggdrasill。在中国的《山海经》中,也有着“建木”的传说,它“有九欘,下有九枸&…...
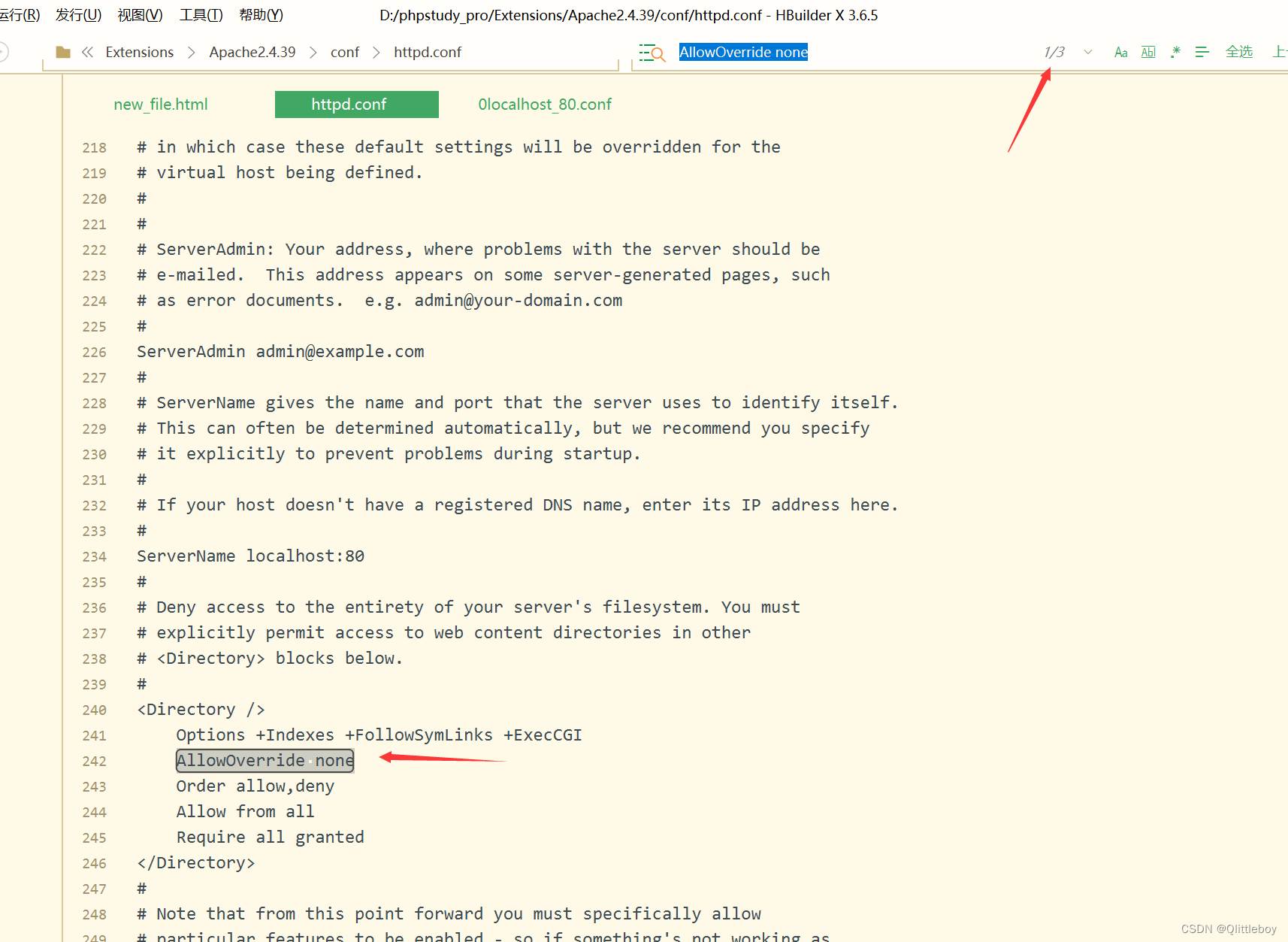
PHPstudy配置伪静态步骤,tp5.1的框架
搜索mod_rewrite.so,然后去掉前面的#(即放开注释) 2.找到index.php 同级文件.htaccess(没有就新建) 这些是tp5.1自带的内容,把它注释掉,是错误的内容,添加下面的这段配置 #<If…...
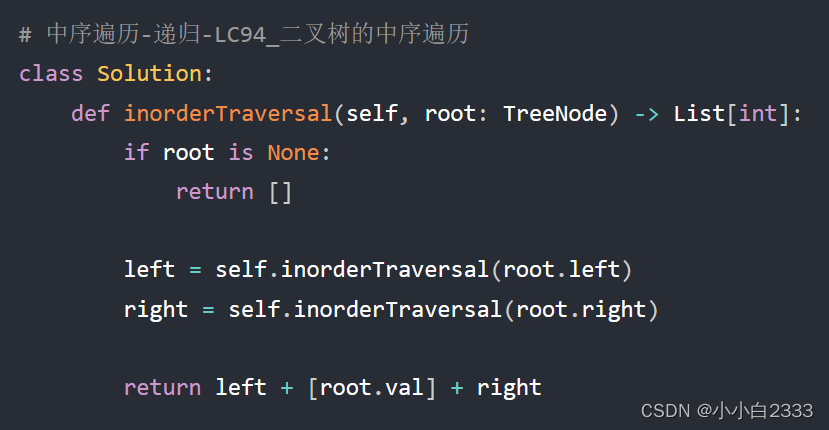
LeetCode:Hot100的python版本
94. 二叉树的中序遍历...
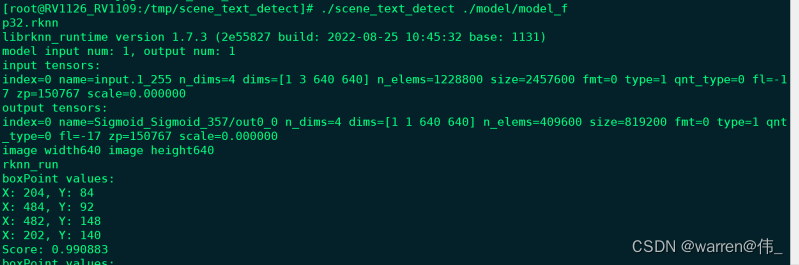
rv1126更新rknpu驱动教学
测试平台:易佰纳rv1126 38板 查看板端版本-------------------------------------------------- 1:查看npu驱动版本 dmesg | grep -i galcore,可以看到版本为6.4.3.5 2:查看rknn-server版本 strings /usr/bin/rknn_server | g…...
[机器学习]线性回归模型
线性回归 线性回归:根据数据,确定两种或两种以上变量间相互依赖的定量关系 函数表达式: y f ( x 1 , x 2 . . . x n ) y f(x_1,x_2...x_n) yf(x1,x2...xn) 回归根据变量数分为一元回归[ y f ( x ) yf(x) yf(x)]和多元回归[ y …...

Vue基于php医院预约挂号系统_6nrhh
随着信息时代的来临,过去的管理方式缺点逐渐暴露,对过去的医院预约挂号管理方式的缺点进行分析,采取计算机方式构建医院预约挂号系统。本文通过阅读相关文献,研究国内外相关技术,开发并设计一款医院预约挂号系统的构建…...

2023-08-07力扣今日六题-不错题
链接: 剑指 Offer 04. 二维数组中的查找 题意: 一个二维矩阵数组,在行上非递减,列上也非递减 解: 虽然在行列上非递减,但是整体并不有序,第一行存在大于第二行的数字,第一列存在…...

Elasticsearch搜索出现NAN异常
原因分析 Elasticsearch默认的打分,一般是不会出现异常的之所以会出现NAN异常,往往是因为我们重新计算了打分,使用了function_score核心原因是在function_score中,出现了计算异常,比如 0/0,比如log1p(x),x为负数等 真…...

(杭电多校)2023“钉耙编程”中国大学生算法设计超级联赛(6)
1001 Count 当k在区间(1n)/2的左边时,如图,[1,k]和[n-k1,n]完全相同,所以就m^(n-k) 当k在区间(1n)/2的右边时,如图,[1,n-k1]和[k,n]完全相同,所以也是m^(n-k) 别忘了特判,当k等于n时,n-k为0,然后a1a1,a2a2,..anan,所以没什么限制,那么就是m^n AC代码: #includ…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...
