【深度学习】模型评估
上一章——多分类问题和多标签分类问题
文章目录
- 算法诊断
- 模型评估
- 交叉验证测试
算法诊断

如果你为问题拟合了一个假设函数,我们应当如何判断假设函数是否适当拟合了?我们可以通过观察代价函数的图像,当代价函数达到最低点的时候,此时的拟合状态是最好的,因此我们才需要对其进行梯度下降。
上图的代价函数J是经过了正则化的,假设当前代价函数J的拟合误差较大,如何来减小误差?在过拟合与正则化这一章中,列举了几种方法,在上图中也写出了:
- 增加训练样本
- 尝试减少特征集
- 增加一些额外的特征
- 添加多项式特征
- 试着改变正则化系数λ
有的时候我们的机器学习算法并不能达到想要的效果,那么也许是哪里出问题了,解决问题并不难,关键在于找到问题出在哪里,因此我们需要对神经网络进行诊断。
诊断是一种测试,我们可以运行它来深入算法,了解算法中那些是有效的,那些是无效的,从而提升算法的性能。因此学习算法诊断是必要的,不过在此之前,我们看看应当如何评估我们的算法。
模型评估
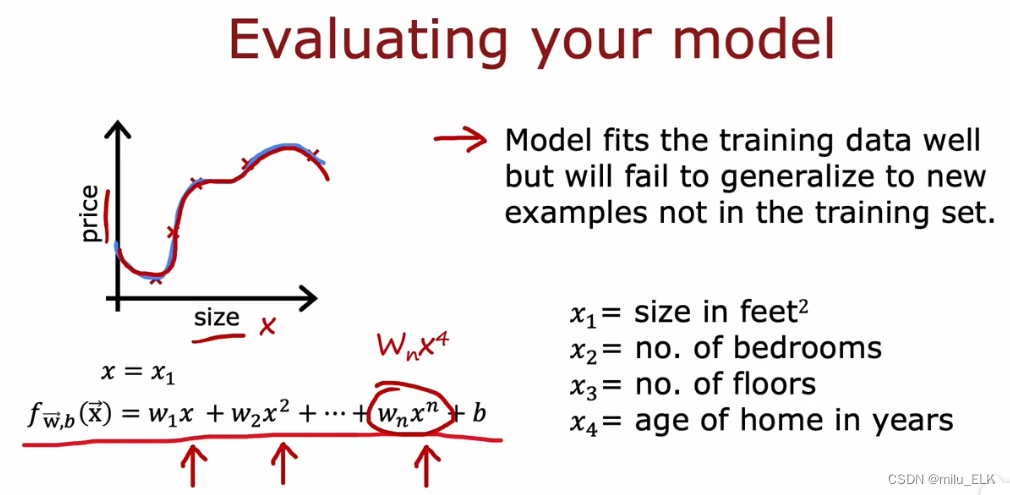
如图是一个四阶多项式的拟合函数,通过观察图像我们知道这个函数的拟合效果很好,但是好到过头了,我们也说过这种过度拟合的状态称为过拟合。如果增加新的数据,这个拟合函数显然是不具有泛化性的,我们认为这样的过拟合的函数不能推广到新的数据集中的数据。并且我们给出了四个特征,而上图中用于函数拟合的只使用了size这一特征,显然只用一个特征拟合也是不适当的。然而哪怕我们想要使用四个特征绘制函数,身为三微生物的我们也无法画出四维图像。
因此上述模型存在两个问题:
- 如何保证拟合其他数据?
- 对于三个以上的特征,我们无法通过图像判断性能,能否更系统地判断模型的性能?
 我们的方法是:将数据集划分为两个子集,其中一个称为训练集(training set),我们取70%,另一个称为测试集,取30%。
我们的方法是:将数据集划分为两个子集,其中一个称为训练集(training set),我们取70%,另一个称为测试集,取30%。
我们用(x,y)(x,y)(x,y)来表示测试样例,其中(xm,ym)(x^m,y^m)(xm,ym)代表训练集第m项测试样例,(xtestm,ytestm)(x^m_{test},y^m_{test})(xtestm,ytestm)来表示测试集第m项测试样例。

接下来,我们可以通过式子①最小化代价函数来找到拟合参数w,bw,bw,b,因为假设函数是包括了多个特征的多项式,因此我们会采取正则化来减小拟合误差。
式子②称为测试误差,通过式子①我们找到了拟合参数w,bw,bw,b,现在将其带入到假设函数,并用式子②算出测试集的测试误差,我们并不是在拟合函数,而是计算测试误差的大小,因此该式子是不用正则化的,最后计算的结果即为测试误差。
式子③与式子②同理。注意,式子①J(w,b)J(w,b)J(w,b)是代价函数,而式子②③中的Jtest(w,b)J_{test}(w,b)Jtest(w,b)和Jtrain(w,b)J_{train}(w,b)Jtrain(w,b),是计算误差的函数,从本质上来讲误差函数(损失函数)和代价函数是一个东西,但是它们的功能并不相同,理解概念并注意区分。
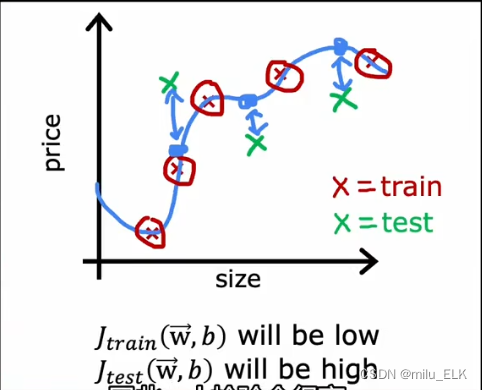
现在让我们看看拟合图像,如果数据点如上图所示(红点代表训练集数据,绿点代表测试集数据),我们会发现一个问题:
Jtrain(w,b)J_{train}(w,b)Jtrain(w,b)较低,代表了训练误差低,这是必然的,因为我们是基于训练集的数据来最小化代价函数进行参数选择的,因此拟合出来的函数的训练误差一定是较小的。(与训练集的误差在于正则化)
然而如果测试集的数据点如图所示,就会发现Jtrain(w,b)J_{train}(w,b)Jtrain(w,b)较高,这代表着测试误差较大,这意味着对于测试集,这个拟合函数的拟合状态并不是很好,因此我们可以认为这个函数并不具有泛化性,这个模型是有问题的。

那么分类问题也是同样的道理,把我们使用分类问题的代价函数(损失函数)来进行计算,
不过在分类问题中,我们对于误差的定义有点不同

在二分问题里,通常我们将0.5作为阈值,当>阈值分类为1,<阈值分类为0,我们将代价函数的预测值称为y^\hat yy^,分类问题中的误差,指的是对于同一个输入样例,有多少个预测值y^\hat yy^与实际值yyy不同,这个误差指的是这些被错误分类的y^\hat yy^的数量比例。
通过训练集和测试集,你可以系统地对模型误差进行评估,从而创建更好的模型。
交叉验证测试

那么假如,我们按照刚才的模型评估的步骤来建立一个拟合函数,我们首先通过训练集的数据的正则化最小化代价函数,找到了合适的w和bw和bw和b,我们将当前的拟合出来的多次项的项数记为d=nd=nd=n,把对应项数的参数记为w<n>,b<n>w^{<n>},b^{<n>}w<n>,b<n>,最后计算的测试误差记为Jtest(w<n>,b<n>)J_{test}(w^{<n>},b^{<n>})Jtest(w<n>,b<n>),现在我们要做的就是找到最小的测试误差JtestJ_{test}Jtest所对应的w,b和dw,b和dw,b和d,现在假设找到了最小测试误差是在当d=5d=5d=5时,我们是否可以认为现在选择的模型是最适宜的?
实际上,答案是否定的,因为我们的估计流程依然存在着问题,导致了JtestJ_{test}Jtest很可能乐观估计了泛化误差,也就是说虽然我们计算出来的测试误差与实际的泛化误差相比可能偏小了,实际误差将会比计算结果要大。原因在于多项式的次数d,因为d是在测试集上确定的,用测试集确定的d来检验测试集的误差,那必然能得到一个较小的误差,就像我给我自己监考,这显然是不公平的。

我们解决问题的方法是:将数据集分为三个子集,训练集60%,交叉验证集20%,测试集20%。其中新加入的交叉验证集(cross validation set)的作用是用于检查不同验证集合的准确性,你也可以叫他验证集(validation set)或者开发集(development set 或dev set)。
 w,bw,bw,b还是用最小化代价函数计算,现在我们要计算的误差总共有三个,它们的公式是一样的,交叉验证集的误差被称为验证误差或者开发误差。
w,bw,bw,b还是用最小化代价函数计算,现在我们要计算的误差总共有三个,它们的公式是一样的,交叉验证集的误差被称为验证误差或者开发误差。

现在再让我们回到之前的步骤,我们首先通过训练集的数据的正则化最小化代价函数计算不同次数的w,bw,bw,b,我们带入验证误差来计算对应次数的JcvJ_{cv}Jcv,假设现在我们找到了d=4d=4d=4时的验证误差最小,那么我们就可以用d,w<4>,b<4>d,w^{<4>},b^{<4>}d,w<4>,b<4>去计算测试误差JtestJ_{test}Jtest,因为w,bw,bw,b是训练集确定的,ddd是交叉验证集确定的,因此没有一个参数与测试集有关,这样就保证我们的误差计算结果相对公平。
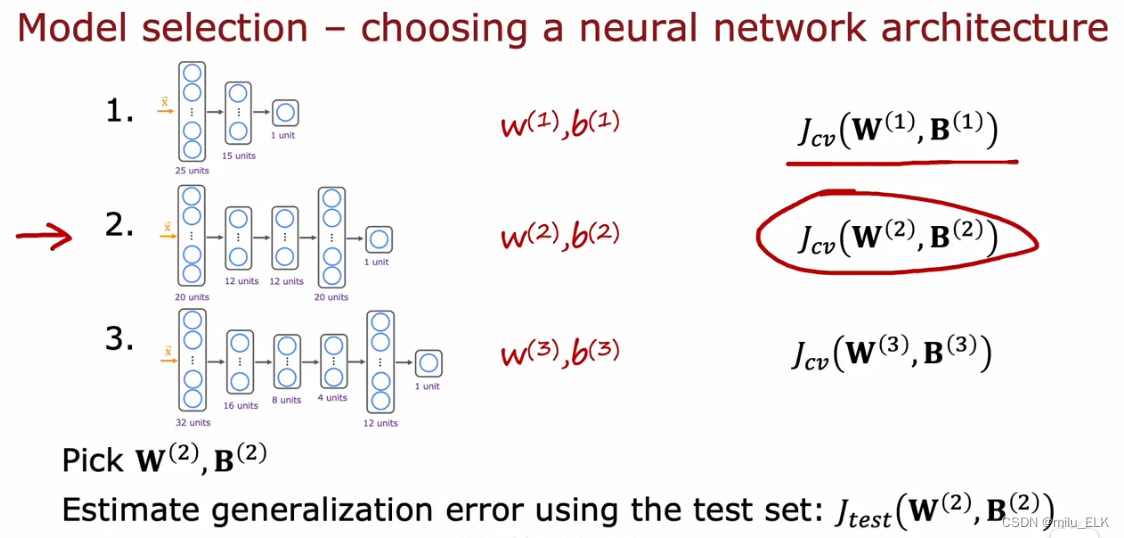 在整个神经网络模型的选择上我们也是这样测试的,例如这三个模型的隐藏层,我们计算得到二号模型的参数对应的验证误差较小,那么我们就可以使用第二个神经网络训练的参数,如果想要得到泛化误差的估计值,我们就可以用这个参数带入计算测试误差JtestJ_{test}Jtest来判断神经网络的性能,使用交叉验证集来选择模型也是目前最佳的决定方法。不过想要作出决定只需要训练集和交叉验证集来确定参数即可,在确定参数之后我们可以在测试集进行评估。这种方法可以确保测试集的公平估计,而非对泛化误差的乐观估计。一个重要原则就是:在未决定模型之前,千万不要使用测试集的数据,来保证估计的公平性。
在整个神经网络模型的选择上我们也是这样测试的,例如这三个模型的隐藏层,我们计算得到二号模型的参数对应的验证误差较小,那么我们就可以使用第二个神经网络训练的参数,如果想要得到泛化误差的估计值,我们就可以用这个参数带入计算测试误差JtestJ_{test}Jtest来判断神经网络的性能,使用交叉验证集来选择模型也是目前最佳的决定方法。不过想要作出决定只需要训练集和交叉验证集来确定参数即可,在确定参数之后我们可以在测试集进行评估。这种方法可以确保测试集的公平估计,而非对泛化误差的乐观估计。一个重要原则就是:在未决定模型之前,千万不要使用测试集的数据,来保证估计的公平性。
相关文章:

【深度学习】模型评估
上一章——多分类问题和多标签分类问题 文章目录算法诊断模型评估交叉验证测试算法诊断 如果你为问题拟合了一个假设函数,我们应当如何判断假设函数是否适当拟合了?我们可以通过观察代价函数的图像,当代价函数达到最低点的时候,此…...

AcWing《蓝桥杯集训·每日一题》—— 3777 砖块
AcWing《蓝桥杯集训每日一题》—— 3777. 砖块 文章目录AcWing《蓝桥杯集训每日一题》—— 3777. 砖块一、题目二、解题思路三、解题思路本次博客我是通过Notion软件写的,转md文件可能不太美观,大家可以去我的博客中查看:北天的 BLOG…...

CleanMyMac X软件下载及详细功能介绍
mac平台的知名系统清理应用CleanMyMac在经历了一段时间的测试后,全新设计的X正式上线。与CleanMyMac3相比,新版本的UI设计焕然一新,采用了完全不同的风格。使用Windows电脑时,很多人会下载各类优化软件,而在Mac平台中&…...

pytorch零基础实现语义分割项目(一)——数据概况及预处理
语义分割之数据加载项目列表前言数据集概况数据组织形式数据集划分数据预处理均值与方差结尾项目列表 语义分割项目(一)——数据概况及预处理 语义分割项目(二)——标签转换与数据加载 语义分割项目(三)…...

ARM+LINUX嵌入式学习路线
嵌入式学习是一个循序渐进的过程,如果是希望向嵌入式软件方向发展的话,目前最常见的是嵌入式Linux方向,关注这个方向,大概分3个阶段: 1、嵌入式linux上层应用,包括QT的GUI开发 2、嵌入式linux系统开发 3、…...
echart在微信小程序的使用
echart在微信小程序的使用 echarts不显示在微信小程序 <!-- 微信小程序的echart的使用 --> <view class"container"><ec-canvas id"mychart-dom-bar" canvas-id"mychart-bar" ec"{{ ec }}"></ec-canvas> &l…...
)
51单片机最强模块化封装(5)
文章目录 前言一、创建timer文件,添加timer文件路径二、timer文件编写三、模块化测试总结前言 今天这篇文章将为大家封装定时器模块,定时器是工程项目中必不可少的,希望大家能够将定时器理解清楚并且运用自如。 一、创建timer文件,添加timer文件路径 这里的操作就不过多…...

链表学习之判断链表是否回文
链表解题技巧 额外的数据结构(哈希表);快慢指针;虚拟头节点; 判断链表是否回文 要求:时间辅助度O(N),空间复杂度O(1) 方法1:栈(不考虑空间复杂度) 遍历一…...
【Linux06-基础IO】4.5万字的基础IO讲解
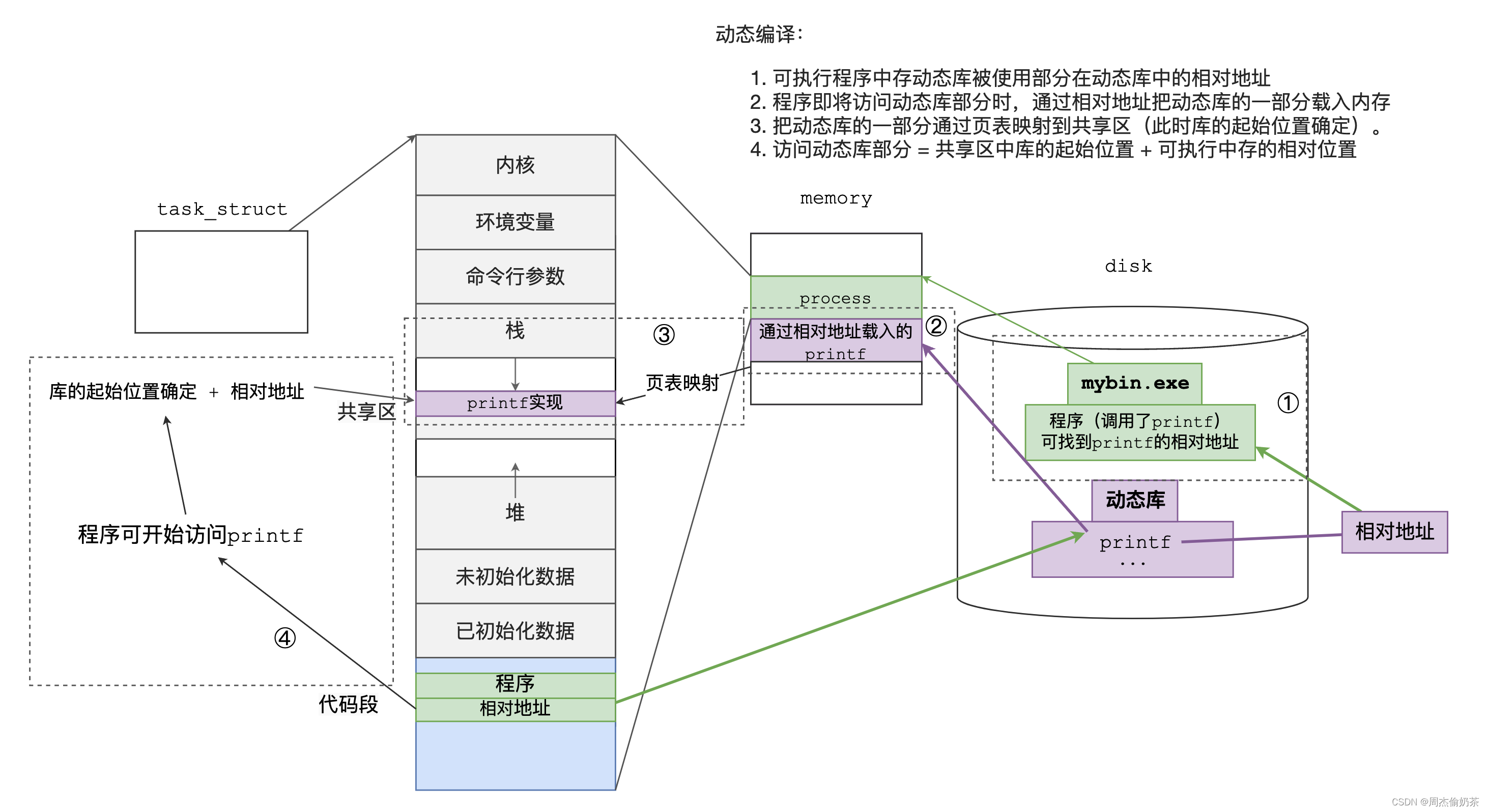
前言 本期分享基础IO的知识,主要有: 复习C语言文件操作文件相关的系统调用文件描述符fd理解Linux下一切皆文件缓冲区文件系统软硬链接动静态库的理解和制作动静态编译 博主水平有限,不足之处望请斧正! C语言文件操作 #再谈文件…...

c++协程库理解—ucontext组件实践
文章目录1.干货写在前面2.ucontext初接触3.ucontext组件到底是什么4.小试牛刀-使用ucontext组件实现线程切换5.使用ucontext实现自己的线程库6.最后一步-使用我们自己的协程库1.干货写在前面 协程是一种用户态的轻量级线程 首先我们可以看看有哪些语言已经具备协程语义&#x…...

英语基础-状语
1. 课前引语 1. 形容词使用场景 (1). 放在系动词后面作表语 The boy is handsome. (2). 放在名词前面做定语 I like this beautiful girl. (3). 放在宾语后面做补语 You make your father happy. 总结:形容词无论做什么,都离不开名词,…...

目标检测笔记(八):自适应缩放技术Letterbox完整代码和结果展示
文章目录自适应缩放技术Letterbox介绍自适应缩放技术Letterbox流程自适应缩放Letterbox代码运行结果自适应缩放技术Letterbox介绍 由于数据集中存在多种不同和长宽比的样本图,传统的图片缩放方法按照固定尺寸来进行缩放会造成图片扭曲变形的问题。自适应缩放技术通…...

2023年全国最新高校辅导员精选真题及答案1
百分百题库提供高校辅导员考试试题、辅导员考试预测题、高校辅导员考试真题、辅导员证考试题库等,提供在线做题刷题,在线模拟考试,助你考试轻松过关。 一、选择题 11.李某与方某签订房屋租赁合同期间,李某欲购买租赁房屋ÿ…...

【Python】Python读写Excel表格
简要版,更多功能参考资料1。1 Excel文件保存格式基础概念此处不提,详见资料1。Excel的文件保存格式有两种: xls 和 xlsx。如果你看不到文件后缀,按下图设置可见。xls是Office 2003及之前版本的表格的默认保存格式。xlsx 是 Excel …...
Python每日一练(20230218)
目录 1. 旋转图像 2. 解码方法 3. 二叉树最大路径和 1. 旋转图像 给定一个 n n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。 你必须在原地旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像…...
基于SSM框架的狼途汽车门店管理系统的设计与实现
基于SSM框架的狼途汽车门店管理系统的设计与实现 ✌全网粉丝20W,csdn特邀作者、博客专家、CSDN新星计划导师、java领域优质创作者,博客之星、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 🍅文末获取项目下载方式🍅 一、…...

视频监控流程图3
<html> <head> <meta http-equiv"Content-Type" content"text/html; charsetUTF-8"/> <link rel"stylesheet" type"text/css" href"visio.css"/> <title> 视频监控流程图 </title> <…...
 2.14.3 CANFD协议介绍)
Linux ARM平台开发系列讲解(CAN) 2.14.3 CANFD协议介绍
1. 概述 前面章节介绍了CAN2.0协议,CAN现在主要是用在汽车领域,随着CAN的发展, 又衍生除了CANFD协议,该协议是在CAN的基础之上进行了升级,CAN2.0的最高速率是1Mbps,有限的速率导致CAN总线上负载率变高,所以CANFD就出现了,CANFD目前最高支持10Mbps。除此之外,CANFD还拥…...

参考 | 给C盘 “搬家“
参考 | 给C盘 “搬家” 将在C盘准备 “搬家” 的 文件/文件夹 完整路径 copy 下来 e.g. 路径一 “C:\Users\你的用户名\AppData\Roaming\kingsoft” 将这个 文件/文件夹 CTRLX 剪切下来 注意: 剪切后, 不需要自己重新新建, 直接执行第三步 将这个 文件/文件夹 CTRLV 粘贴到你要…...
剑指 Offer 53 - II. 0~n-1中缺失的数字
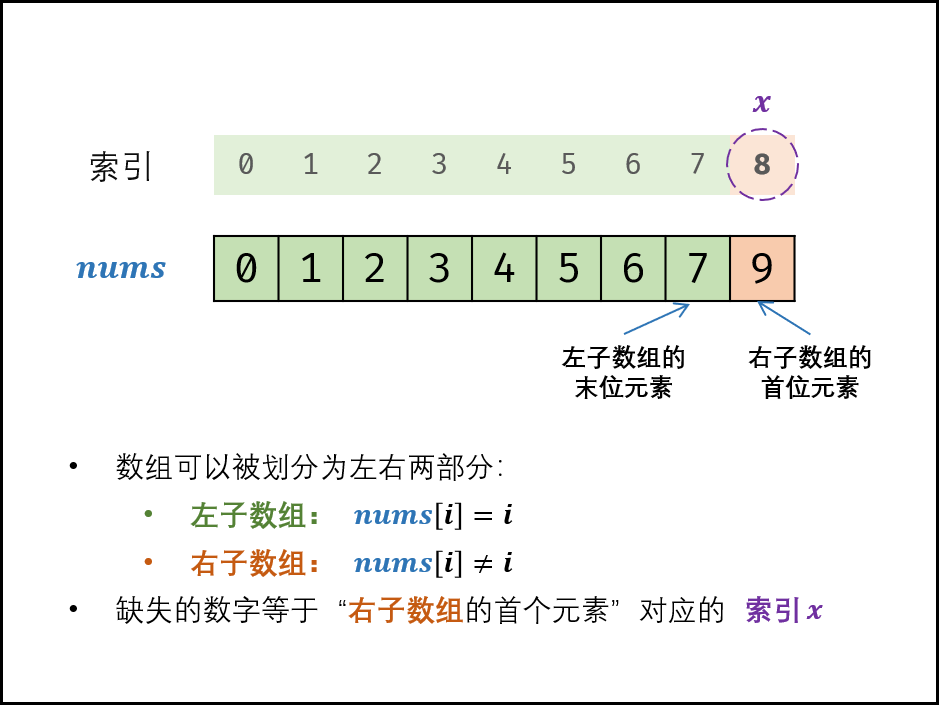
原题链接 难度:easy\color{Green}{easy}easy 题目描述 一个长度为n-1的递增排序数组中的所有数字都是唯一的,并且每个数字都在范围0~n-1之内。在范围0~n-1内的n个数字中有且只有一个数字不在该数组中,请找出这个数字…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...

Qemu arm操作系统开发环境
使用qemu虚拟arm硬件比较合适。 步骤如下: 安装qemu apt install qemu-system安装aarch64-none-elf-gcc 需要手动下载,下载地址:https://developer.arm.com/-/media/Files/downloads/gnu/13.2.rel1/binrel/arm-gnu-toolchain-13.2.rel1-x…...

Matlab实现任意伪彩色图像可视化显示
Matlab实现任意伪彩色图像可视化显示 1、灰度原始图像2、RGB彩色原始图像 在科研研究中,如何展示好看的实验结果图像非常重要!!! 1、灰度原始图像 灰度图像每个像素点只有一个数值,代表该点的亮度(或…...
