代码随想录算法训练营day57
文章目录
- Day57
- 回文子串
- 题目
- 思路
- 代码
- 最长回文子序列
- 题目
- 思路
- 代码
Day57
回文子串
647. 回文子串 - 力扣(LeetCode)
题目
给你一个字符串 s ,请你统计并返回这个字符串中 回文子串 的数目。
回文字符串 是正着读和倒过来读一样的字符串。
子字符串 是字符串中的由连续字符组成的一个序列。
具有不同开始位置或结束位置的子串,即使是由相同的字符组成,也会被视作不同的子串。
思路
动规五部曲
- 确定dp数组以及下标含义
本题如果我们定义,dp[i] 为 下标i结尾的字符串有 dp[i]个回文串的话,我们会发现很难找到递归关系。
dp[i] 和 dp[i-1] ,dp[i + 1] 看上去都没啥关系。
所以我们要看回文串的性质。 如图:
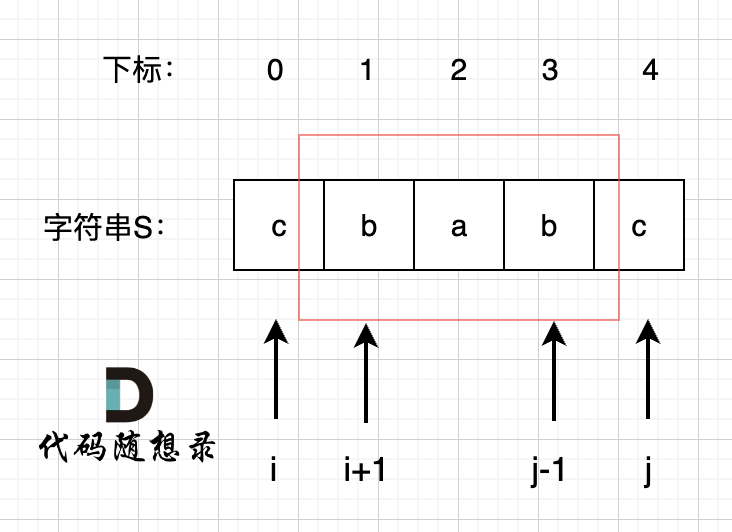
我们在判断字符串S是否是回文,那么如果我们知道 s[1],s[2],s[3] 这个子串是回文的,那么只需要比较 s[0]和s[4]这两个元素是否相同,如果相同的话,这个字符串s 就是回文串。
那么此时我们是不是能找到一种递归关系,也就是判断一个子字符串(字符串的下表范围[i,j])是否回文,依赖于,子字符串(下表范围[i + 1, j - 1])) 是否是回文。
所以为了明确这种递归关系,我们的dp数组是要定义成一位二维dp数组。
布尔类型的dp[i][j]:表示区间范围[i,j] (注意是左闭右闭)的子串是否是回文子串,如果是dp[i][j]为true,否则为false。
- 确定递推公式
在确定递推公式时,就要分析如下几种情况。
整体上是两种,就是s[i]与s[j]相等,s[i]与s[j]不相等这两种。
当s[i]与s[j]不相等,那没啥好说的了,dp[i][j]一定是false。
当s[i]与s[j]相等时,这就复杂一些了,有如下三种情况
-
情况一:下标i 与 j相同,同一个字符例如a,当然是回文子串
-
情况二:下标i 与 j相差为1,例如aa,也是回文子串
-
情况三:下标:i 与 j相差大于1的时候,例如cabac,此时s[i]与s[j]已经相同了,我们看i到j区间是不是回文子串就看aba是不是回文就可以了,那么aba的区间就是 i+1 与 j-1区间,这个区间是不是回文就看dp[i + 1][j - 1]是否为true。
if(s.charAt(i) == s.charAt(j)){
if (j - i <= 1){ // 情况一, 情况二
count++;
dp[i][j] = true;
}else if(dp[i + 1][j - 1]){ // 情况三
count++;
dp[i][j] = true;
}
}
result就是统计回文子串的数量。
注意这里我没有列出当s[i]与s[j]不相等的时候,因为在下面dp[i][j]初始化的时候,就初始为false。
- dp数组初始化
dp[i][j]初始化为false。
- 遍历顺序
首先从递推公式中可以看出,情况三是根据dp[i + 1][j - 1]是否为true,在对dp[i][j]进行赋值true的。
dp[i + 1][j - 1] 在 dp[i][j]的左下角,如图:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Wis0JIQb-1691292330556)(https://code-thinking-1253855093.file.myqcloud.com/pics/20210121171032473-20230310132134822.jpg “647.回文子串”)]
如果这矩阵是从上到下,从左到右遍历,那么会用到没有计算过的dp[i + 1][j - 1],也就是根据不确定是不是回文的区间[i+1,j-1],来判断了[i,j]是不是回文,那结果一定是不对的。
所以一定要从下到上,从左到右遍历,这样保证dp[i + 1][j - 1]都是经过计算的。
有的代码实现是优先遍历列,然后遍历行,其实也是一个道理,都是为了保证dp[i + 1][j - 1]都是经过计算的。
for(int i = sLen - 1; i >= 0; i--){for(int j = i; j < sLen; j++){if(s.charAt(i) == s.charAt(j)){if (j - i <= 1){ // 情况一, 情况二count++;dp[i][j] = true;}else if(dp[i + 1][j - 1]){ // 情况三count++;dp[i][j] = true;}}}
}
- 举例递推公式
举例,输入:“aaa”,dp[i][j]状态如下:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-FfEMQWFb-1691292330556)(https://code-thinking-1253855093.file.myqcloud.com/pics/20210121171059951-20230310132153163.jpg “647.回文子串1”)]
图中有6个true,所以就是有6个回文子串。
注意因为dp[i][j]的定义,所以j一定是大于等于i的,那么在填充dp[i][j]的时候一定是只填充右上半部分。
代码
class Solution {public int countSubstrings(String s) {int sLen = s.length();int count = 0;boolean dp[][] = new boolean[sLen][sLen];for(int i = sLen - 1; i >= 0; i--){for(int j = i; j < sLen; j++){/**整体上是两种,就是s[i]与s[j]相等,s[i]与s[j]不相等这两种。当s[i]与s[j]不相等,dp[i][j]一定是false。当s[i]与s[j]相等时,这就复杂一些了,有如下三种情况情况一:下标i 与 j相同,同一个字符例如a,当然是回文子串情况二:下标i 与 j相差为1,例如aa,也是回文子串情况三:下标:i 与 j相差大于1的时候,例如cabac,此时s[i]与s[j]已经相同了,我们看i到j区间是不是回文子串就看aba是不是回文就可以了,那么aba的区间就是 i+1 与 j-1区间,这个区间是不是回文就看dp[i + 1][j - 1]是否为true。*/if(s.charAt(i) == s.charAt(j)){if (j - i <= 1){ // 情况一, 情况二count++;dp[i][j] = true;}else if(dp[i + 1][j - 1]){ // 情况三count++;dp[i][j] = true;}}}}return count;}
}
最长回文子序列
516. 最长回文子序列 - 力扣(LeetCode)
题目
给定一个字符串 s ,找到其中最长的回文子序列,并返回该序列的长度。可以假设 s 的最大长度为 1000 。
示例 1: 输入: “bbbab” 输出: 4 一个可能的最长回文子序列为 “bbbb”。
示例 2: 输入:“cbbd” 输出: 2 一个可能的最长回文子序列为 “bb”。
提示:
- 1 <= s.length <= 1000
- s 只包含小写英文字母
思路
回文子串是要连续的,回文子序列可不是连续的! 回文子串,回文子序列都是动态规划经典题目。
动规五部曲分析
- 确定dp数组(dp table)以及下标的含义
dp[i][j]:字符串s在[i, j]范围内最长的回文子序列的长度为dp[i][j]。
- 确定递推公式
在判断回文子串的题目中,关键逻辑就是看s[i]与s[j]是否相同。
如果s[i]与s[j]相同,那么dp[i][j] = dp[i + 1][j - 1] + 2;
如图: [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-sCwR202k-1691292330556)(https://code-thinking-1253855093.file.myqcloud.com/pics/20210127151350563.jpg “516.最长回文子序列”)]
(如果这里看不懂,回忆一下dp[i][j]的定义)
如果s[i]与s[j]不相同,说明s[i]和s[j]的同时加入 并不能增加[i,j]区间回文子序列的长度,那么分别加入s[i]、s[j]看看哪一个可以组成最长的回文子序列。
加入s[j]的回文子序列长度为dp[i + 1][j]。
加入s[i]的回文子序列长度为dp[i][j - 1]。
那么dp[i][j]一定是取最大的,即:dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-znfAuWDQ-1691292330557)(https://code-thinking-1253855093.file.myqcloud.com/pics/20210127151420476.jpg “516.最长回文子序列1”)]
if(s.charAt(i) == s.charAt(j)){dp[i][j] = dp[i + 1][j - 1] + 2;
}else{dp[i][j] = Math.max(dp[i + 1][j], dp[i][j - 1]);
}
- dp数组如何初始化
首先要考虑当i 和j 相同的情况,从递推公式:dp[i][j] = dp[i + 1][j - 1] + 2; 可以看出 递推公式是计算不到 i 和j相同时候的情况。
所以需要手动初始化一下,当i与j相同,那么dp[i][j]一定是等于1的,即:一个字符的回文子序列长度就是1。
其他情况dp[i][j]初始为0就行,这样递推公式:dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]); 中dp[i][j]才不会被初始值覆盖。
- 确定遍历顺序
从递归公式中,可以看出,dp[i][j] 依赖于 dp[i + 1][j - 1] ,dp[i + 1][j] 和 dp[i][j - 1],如图:
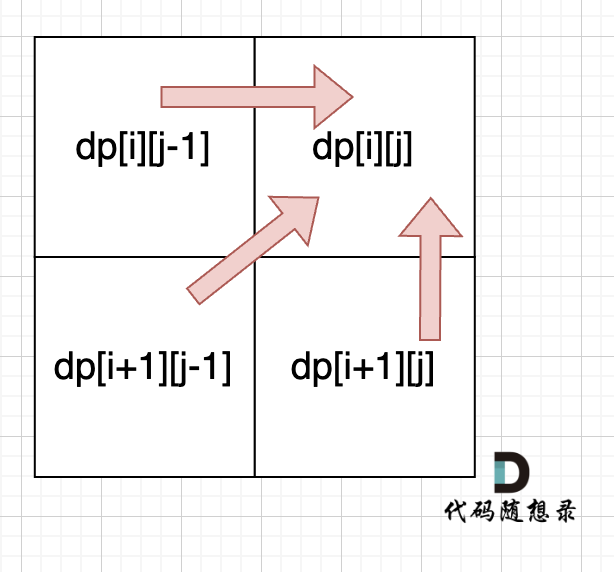
所以遍历i的时候一定要从下到上遍历,这样才能保证下一行的数据是经过计算的。
j的话,可以正常从左向右遍历。
for(int i = sLen - 1; i >= 0; i--){for(int j = i + 1; j < sLen; j++){if(s.charAt(i) == s.charAt(j)){dp[i][j] = dp[i + 1][j - 1] + 2;}else{dp[i][j] = Math.max(dp[i + 1][j], dp[i][j - 1]);}}
}
- 举例推导dp数组(一定要推导)
输入s:“cbbd” 为例,dp数组状态如图:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-wh0U0pFO-1691292330557)(https://code-thinking-1253855093.file.myqcloud.com/pics/20210127151521432.jpg “516.最长回文子序列3”)]
红色框即:dp[0][s.size() - 1]; 为最终结果。
代码
class Solution {public int longestPalindromeSubseq(String s) {int sLen = s.length();// dp[i][j]:字符串s在[i, j]范围内最长的回文子序列的长度为dp[i][j]。int dp[][] = new int[sLen][sLen];for(int i = 0; i < sLen; i++) dp[i][i] = 1;for(int i = sLen - 1; i >= 0; i--){for(int j = i + 1; j < sLen; j++){if(s.charAt(i) == s.charAt(j)){dp[i][j] = dp[i + 1][j - 1] + 2;}else{dp[i][j] = Math.max(dp[i + 1][j], dp[i][j - 1]);}}}return dp[0][sLen - 1];}
}
相关文章:

代码随想录算法训练营day57
文章目录 Day57回文子串题目思路代码 最长回文子序列题目思路代码 Day57 回文子串 647. 回文子串 - 力扣(LeetCode) 题目 给你一个字符串 s ,请你统计并返回这个字符串中 回文子串 的数目。 回文字符串 是正着读和倒过来读一样的字符串。…...

【基础类】—前后端通信类系统性学习
一、什么是同源策略及限制 同源策略限制从一个源加载的文档或脚本如何与来自另一个源的资源进行交互。这是一个用于隔离潜在恶意文件的关键的安全机制。源:协议、域名和端口, 默认端口是80 三者有一个不同,即源不同,就是跨域 ht…...
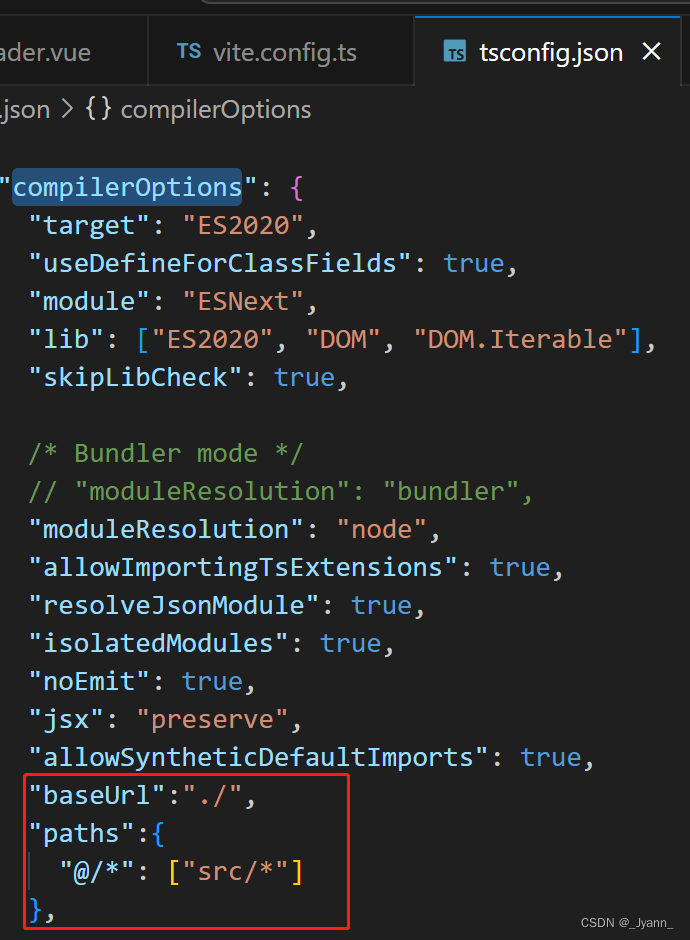
vite项目中使用@代表根路径
1.配置vite.config.ts import { defineConfig } from vite import vue from vitejs/plugin-vue import path from pathexport default defineConfig({plugins: [vue()],resolve: {alias:{: path.resolve(__dirname, src) }} })2.报错path和__dirname 找不到模块“path”或其相…...

冶金化工操作VR虚拟仿真实验软件提高员工们协同作业的配合度
对于高风险行业来说,开展安全教育培训是企业的重点工作,传统培训逐渐跟不上时代变化和工人需求,冶金安全VR模拟仿真培训系统作为一种新型的教育和培训工具,借助VR虚拟现实技术为冶金行业的工人提供一个安全、高效的培训环境。 冶金…...

SQL Server数据库 -- 索引与视图
文章目录 一、索引 聚集索引非聚集索引二、视图三、自定义函数 标量函数表值函数四、游标五、总结 前言 在学习完创建库表、查询等知识点后,为了更加方便优化数据库的存储和内容,我们需要学习一系列的方法例如索引与视图等等,从而使我们更加…...

2023 java web面试秘籍
目录 第一章:Java Web基础知识1.介绍3.Java Web基本概念 4.常见面试问题第二章:Java Web核心概念和技术1.介绍3.Servlet和JSP4.Web安全5.常见面试问题 第三章:Java Web高级概念和技术1.介绍3.Spring框架4.安全性5.常见面试问题 第四章&#x…...

2023-08-05力扣今日二题
链接: 剑指 Offer 18. 删除链表的节点 题意: 如题 解: 基础链表操作 实际代码: #include<iostream> using namespace std; struct ListNode {int val;ListNode *next;ListNode(int x) : val(x), next(NULL) {} }; Li…...
stl_list类(使用+实现)(C++)
list 一、list-简单介绍二、list的常用接口1.常见构造2.iterator的使用3.Capacity和Element access4.Modifiers5.list的迭代器失效 三、list实现四、vector 和 list 对比五、迭代器1.迭代器的实现2.迭代器的分类(按照功能分类)3.反向迭代器(1)、包装逻辑…...

利用hfish反控境外攻击源主机
导师给了7个网络安全课题选题,本想和他聊了下思路,他一挥手让我先做出点东西再来聊就把我打发走了…… 正好前段时间阿里云到校做推广,用优惠卷薅了一台云服务器,装了hfish先看下情况 没想到才装上没两天数据库就爆了࿰…...

4、Rocketmq之存储原理
CommitLog ~ MappedFileQueue ~ MappedFile集合...
在线原型设计工具有好用的吗?就是这10个
随着设计工作的不断发展,原型设计在设计工作中越来越重要,而在线原型设计工具在减轻了设计师工作负担的同时也提高了设计师的工作效率,今天本文将为大家推荐10个能在线使用的原型设计工具,一起来看看吧! 1、即时设计 …...
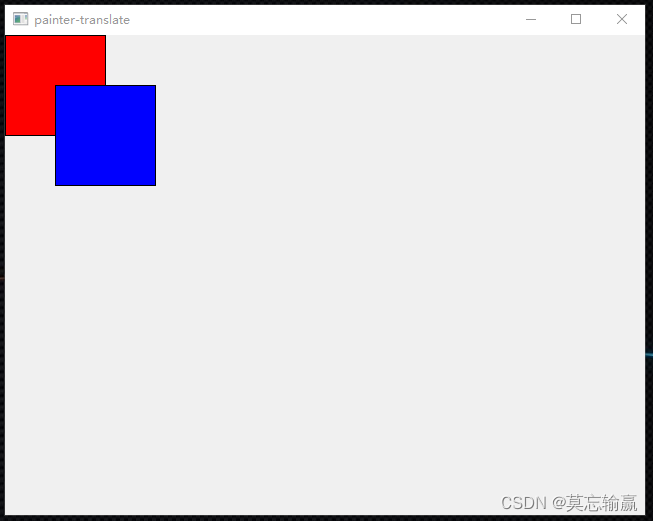
Vc - Qt - QPainter translate
QPainter的translate()函数是用来对绘制坐标系统进行平移操作的方法。它可以将绘制的原点(坐标轴的起始点)在水平和垂直方向上进行平移。以下是一个使用QPainter的translate()方法进行坐标平移的示例代码: QPainter painter(this);// 绘制一个…...

Spark Catalog详解
前言 旁边的实习生说:我想要用spark代码中对hive库中的内部表和外部表进行批量删除(包括数据),咋感觉网上搜了一圈都找不到解决方案啊,spark这么鸡肋吗? 我:你应该静下心来好好把spark基础知识进行全面学习。 实习生:难道spark有这功能,而我没有学习过?咋弄啊? 我:…...
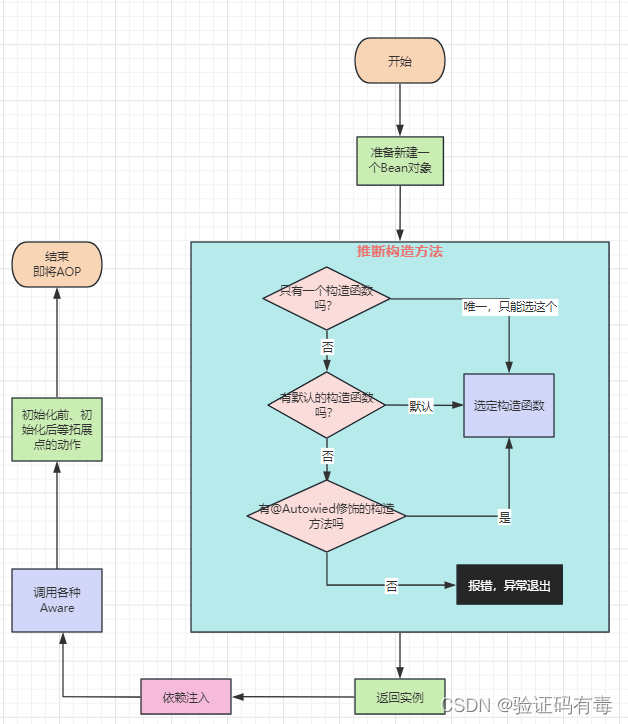
【Spring专题】手写简易Spring容器过程分析
前置知识 《【Spring专题】Spring底层核心原理解析》 思路整理 我们在上一节《【Spring专题】Spring底层核心原理解析》课里面有简单分析过一个Spring容器的一般流程,所以,本节课我们这里尝试写一下简易的Spring容器。 手写源码示例 一、手写前的准…...

fastadmin自定义键值组件Fieldlist
需求场景: 后台设置前端的固定话费充值金额。编辑时要求能够增删改,给到前端的数据,是要根据金额正序排列,用fastadmin的键值组件(Fieldlist),使用Art-Template模板语法自定义模板。 最终效果如下图所示: …...

yolov2检测网数据集标注_labelme使用_json2txt格式转换
yolov2检测网数据集标注_labelme使用_json2txt格式转换 一、安装Anaconda二、创建labelme虚拟环境三、使用labelme标注健康非健康猫狗数据3.1 打开数据集所在文件夹3.2 进行标注数据集3.3 json2txt3.4 按文件目录和训练测试数据集重分配 四、数据喂给服务器网络参考链接 一、安…...
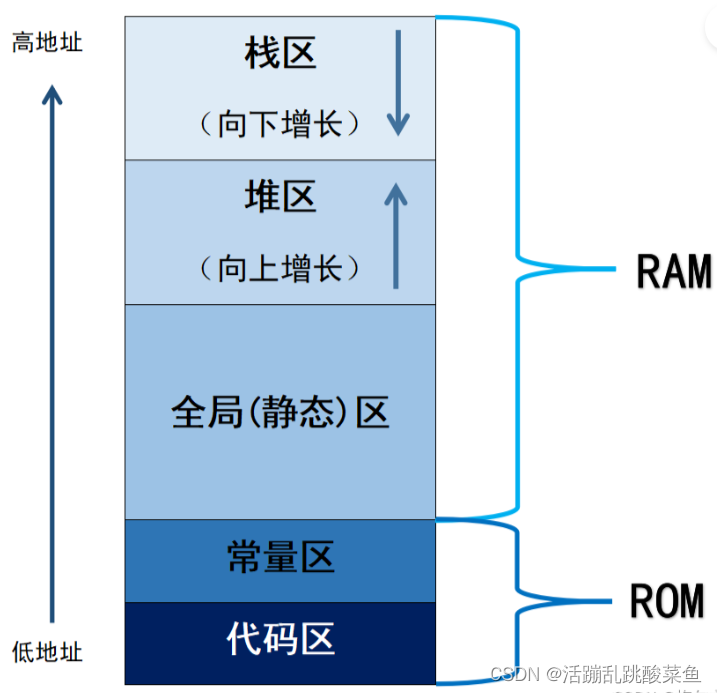
C/C++面试总结
一、关键字static、const、extern、volatile作用 1、const 1.修饰常量 用const修饰的变量是不可变的,修饰后的变量只能使用,不能修改。 2.修饰指针 如果const位于*的左侧,eg:const int* a,则const就是用来修饰指针…...
Python爬虫的Selenium(学习于b站尚硅谷)
目录 一、Selenium 1.为什么要学习Selenium (1)什么是Selenium (2)为什么使用selenium? (3)代码演示 2. selenium的基本使用 (1)如何安装selenium (2…...
springboot 对接 minio 分布式文件系统
1. minio介绍 Minio 是一个基于Go语言的对象存储服务。它实现了大部分亚马逊S3云存储服务接口,可以看做是是S3的开源版本,非常适合于存储大容量非结构化的数据,例如图片、视频、日志文件、备份数据和容器/虚拟机镜像等,而一个对象…...

前端小练习:案例4.3D图片旋转展示(旋转木马)
一.效果预览图 二.实现思路 1.实现旋转木马效果的第一步是先准备好自己需要的图片,创建html文件 2.旋转木马的实现,关键点在3D形变和关键帧动画。 3.步骤,定义一个div使其居中,,把图片放进div盒子里,因为图…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...
