CF1795E Explosions? (单调栈)
传送门
题意:
有 n 个怪兽需要消灭,它们的生命值分别是 h [1],h [2]......h [n].
我们可以使用两种技能:
技能 1:选择任意一个怪兽,使其生命值降低 1 点,并且需要 1 点能量值.
技能 2:选择任意一个怪兽,使其生命值降低 x 点,需要花费 x 点能量值.
如果使用技能 2之后消灭了被选择的怪兽,那么会接着对其相邻的怪兽造成 h[ i ] - 1点伤害值. 注意:技能 2 只能使用一次!
问题:
消灭所有的怪兽最少需要花费多少能量值 ?
思路:
假设把第 i 个怪兽作为Explosion的目标,那么要求 h[1] -> h[ i ] 变成严格单调递增,h[ i ] -> h[ n ]变成严格单调递减.
我们称把 1~ i 的生命值修改为严格单调递增的代价为 L[ i ],i 到 n 的生命值修改为严格单调递减的代价是 R[ i ].
那么答案就是 min {L[ i ] + R[ i ] + h[ i ] },那么现在,问题变成了如果求出 L[ i ] 和 R[ i ].
我们只需要考虑如果求出 L[ i ]即可,因为R[ i ]可以用类似的方法求得.
考虑一个经典技术:单调栈.
做法:
单调栈:
从左到右扫一遍过去.
栈中维护一个二元组(hi,cnt)表示当前有一个怪兽血量为h[ i ],在它左边有 cnt - 1个怪兽,它们的血量从左到右单调递增且差值为 1.
栈中 h[ i ]严格单调递增.
当扫描到 i 时,实时维护一个sum,表示当前的L[ i ],如果h[ i ] > 栈顶的 h,则L[ i ] = sum,并将(hi,1)加入栈,否则,要把栈顶的(h,cnt)这cnt 个怪兽的血量全部减去 h - hi +1,才能满足条件,我们把原先的栈顶 pop.
重复这个过程,直到栈为空或者 hi > 栈顶的 h,最终,我们将(hi,cnt1)加入栈,这里的cnt1表示 1 + pop出来的cnt的和.
参考代码:
#include <bits/stdc++.h>using LL = long long;int main() {std::ios::sync_with_stdio(false);std::cin.tie(nullptr);int t;std::cin >> t;while (t--) {int n;std::cin >> n;std::vector<int> h(n);for (int i = 0; i < n; i++) {std::cin >> h[i];}std::vector<LL> L(n);std::vector<LL> R(n);for (int rot = 0; rot < 2; rot++) {std::vector<std::pair<LL, LL>> st;LL sum{};for (int i = 0; i < n; i++) {LL cnt = 1;while (!st.empty() && h[i] - cnt < st.back().first) {LL diff = st.back().first - (h[i] - cnt);sum += diff * st.back().second;cnt += st.back().second;st.pop_back();}if (cnt - 1 > h[i]) {LL extra = cnt - 1 - h[i];sum -= extra * (extra + 1) >> 1;cnt = h[i];}L[i] = sum;st.emplace_back(h[i], cnt);}std::reverse(L.begin(), L.end());std::reverse(R.begin(), R.end());std::reverse(h.begin(), h.end());std::swap(L, R);}LL ans = (LL)1e18;for (int i = 0; i < n; i++) {ans = std::min(ans, L[i] + R[i] + h[i]);}std::cout << ans << '\n';}return 0;
}相关文章:
)
CF1795E Explosions? (单调栈)
传送门 题意: 有 n 个怪兽需要消灭,它们的生命值分别是 h [1],h [2]......h [n]. 我们可以使用两种技能: 技能 1:选择任意一个怪兽,使其生命值降低 1 点,并且需要 1 点能量值. 技能 2:选择任意…...
C++——二叉树排序树
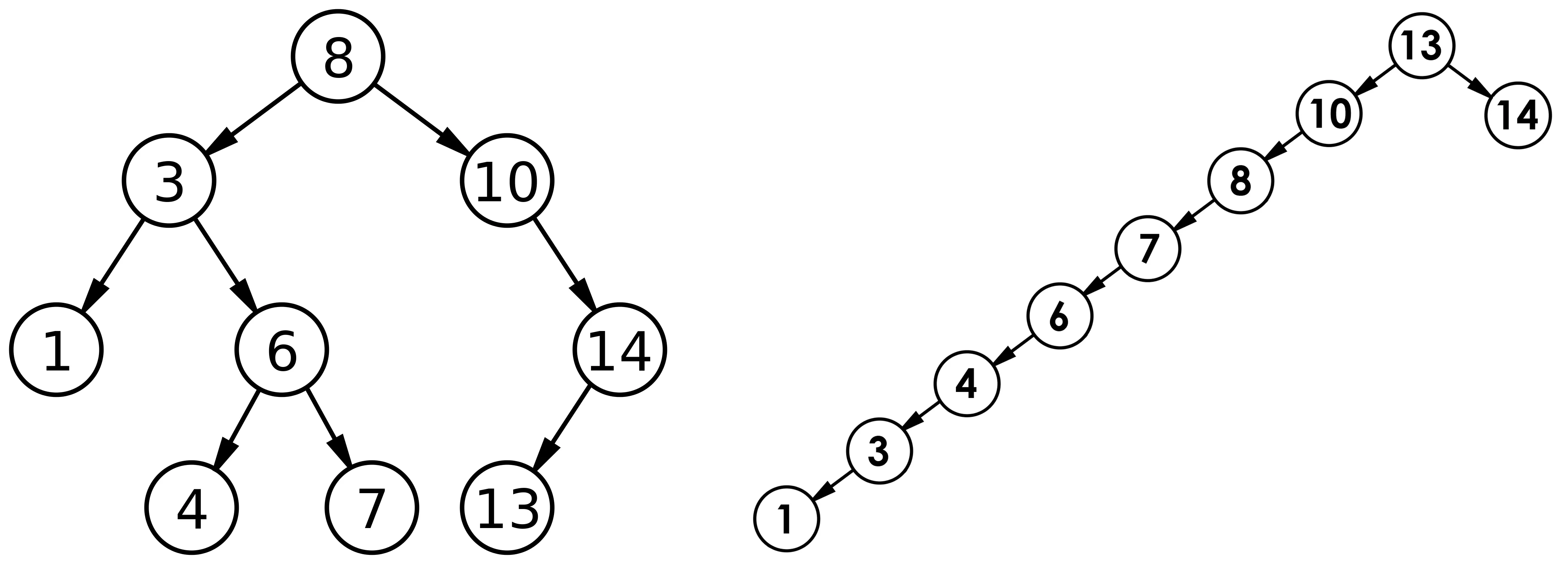
文章目录1 二叉搜索树概念2 二叉搜索树操作与模拟实现2.1 二叉搜索树的查找非递归版本递归版本2.2 二叉搜索树的插入非递归版本递归版本2.3 二叉搜索树的删除非递归版本递归版本3 二叉搜索树的应用(K模型、KV模型)4 二叉搜索树的性能分析1 二叉搜索树概念…...
深拷贝浅拷贝的区别?如何实现一个深拷贝?
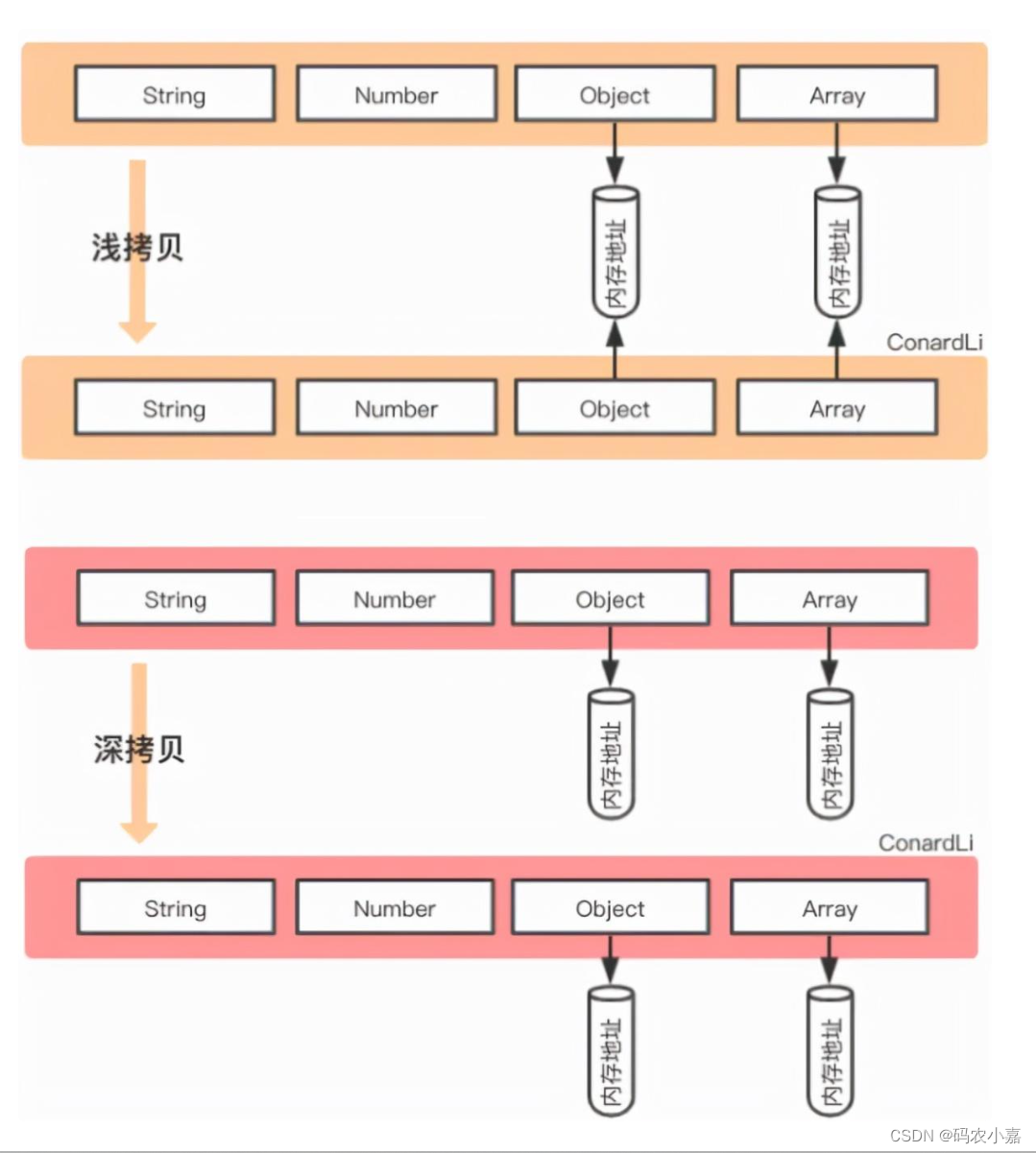
一、数据类型存储 JavaScript中存在两大数据类型: 基本类型 Number String null Undefined Boolean symbol引用类型 array object function 基本类型数据保存在在栈内存中 引用类型数据保存在堆内存中,引用数据类型的变量是一个指向堆内存中实际对象的…...
Linux应用编程下连接本地数据库进行增删改查系列操作
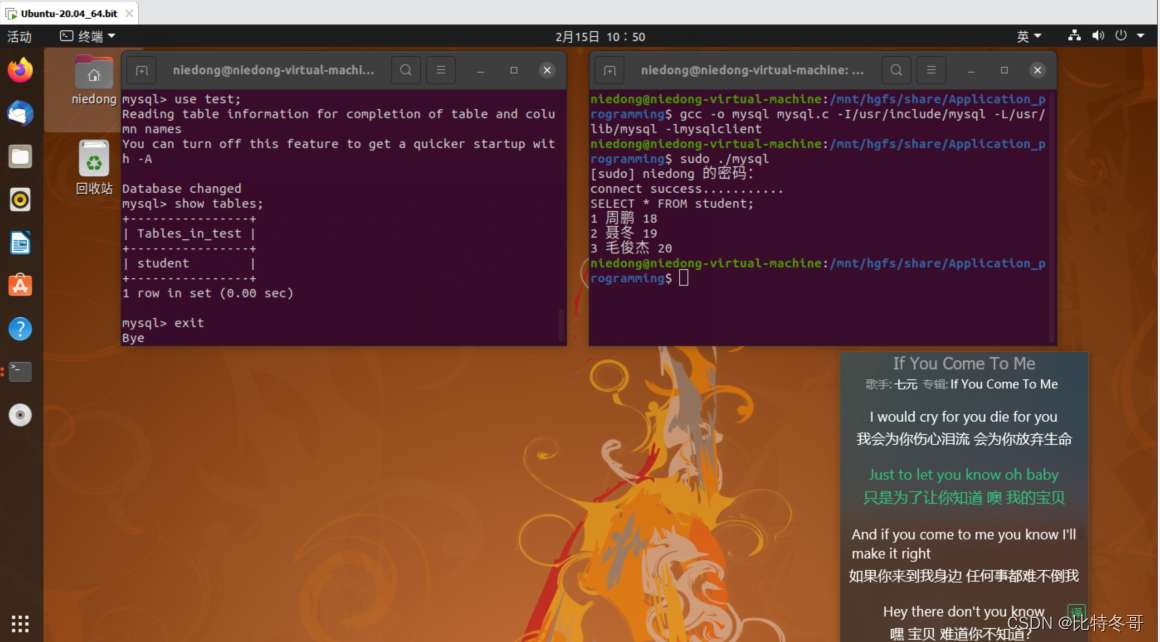
文章目录前言一、常用SQL操作语句二、相关函数解析三、连接本地数据库四、编译运行五、程序源码前言 本篇为C语言应用编程下连接Linux本地数据库进行增删改查系列操作。 在此之前,首先当然是你需要具备一定的数据库基础,所以下面我先列出部分常用的SQL…...

图论学习03
图神经网络模型介绍 将图神经网络分为基于谱域上的模型和基于空域上的模型,并按照发展顺序详解每个类别中的重要模型。 基于谱域的图神经网络 谱域上的图卷积在图学习迈向深度学习的发展历程上起到了关键性的作用。三个具有代表性的谱域图神经网络 谱图卷积网络切…...

解决qt中cmake单独存放 .ui, .cpp, .h文件
设想 项目文件较多,全部放在一个目录下就像依托答辩。 希望能将头文件放入include,ui文件放入ui,源文件放入src。 为了将Qt代码和一般非Qt代码分离开,进一步地: 将Qt源文件放入qt_src,普通源文件放入sr…...

操作系统(day12)-- 基本分段存储,段页式存储
基本分段存储管理方式 不会产生内部碎片,会产生外部碎片 分段 按照程序自身的逻辑关系划分为 若干个段,每个段都有一个段名,每段从0开始编址 分段存储管理方式中一个段表项由段号(隐含)、段长、基地址 分段的段表项固…...

疯狂弹出请插入多卷集的最后一张磁盘窗口
整个人嘛了,今天插上U盘,跟tmd中了病毒一样, 屏幕疯狂弹出窗口, 提示请插入多卷集的最后一张磁盘! 点确定之后他继续弹出,点取消它也继续弹出, 关掉一个又弹出来一个,妈的&#x…...
Spark12: SparkSQL入门
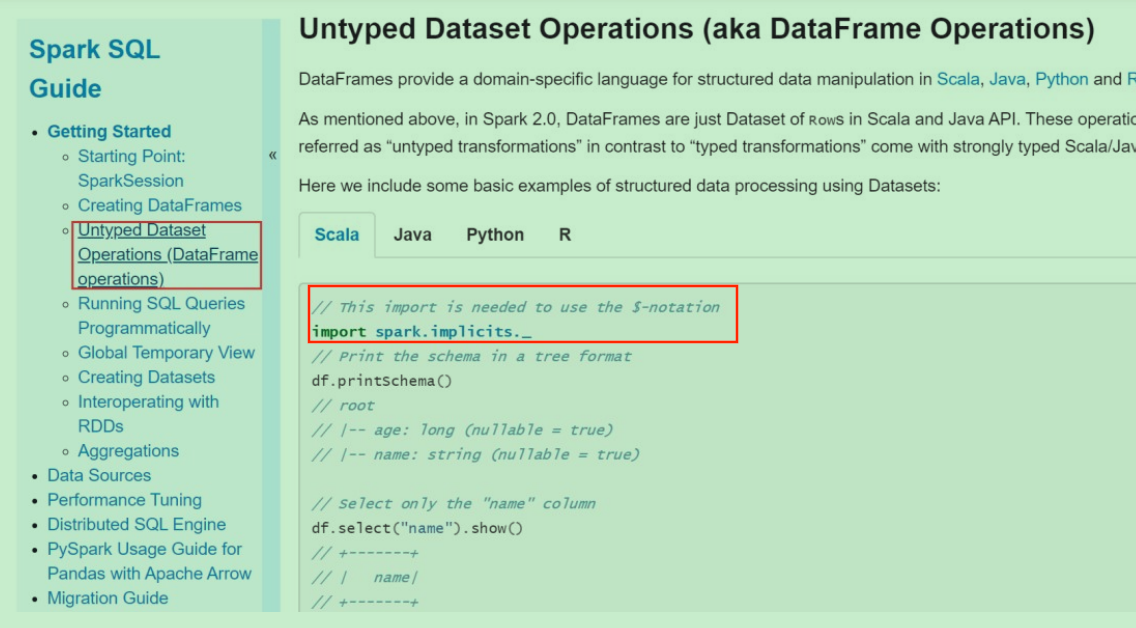
一、SparkSQL Spark SQL和我们之前讲Hive的时候说的hive on spark是不一样的。hive on spark是表示把底层的mapreduce引擎替换为spark引擎。而Spark SQL是Spark自己实现的一套SQL处理引擎。Spark SQL是Spark中的一个模块,主要用于进行结构化数据的处理。它提供的最核…...

show profile和trance分析SQL
目录 一.show profile分析SQL 二.trance分析优化器执行计划 一.show profile分析SQL Mysql从5.0.37版本开始增加了对show profiles和show profile语句的支持。show profiles能够在做SQL优化时帮助我们了解时间都耗费到哪里去了。。 通过have_profiling参数,能够…...
[AI生成图片] 效果最好的Midjourney 的介绍和使用
Midjourney介绍: 是一个文本生成图片的扩散模型,能够根据输入的任何文本生成令人难以置信的图像,让数十亿人在几秒钟内创造惊人的艺术。为方便用户控制和快速生成图片,打开后在页面底部输入文本内容,稍等一小会&#…...
 的核心原理)
Vue.use( ) 的核心原理
首先来思考几个问题: Vue.use是什么? vue.use() 是vue提供的一个静态方法,主要是为了注册插件,增加vue的功能。 Vue.use( plugin ) plugin只能是Object 或 Function vue.use()做了什么工作? 该js如果是对象 该对象…...
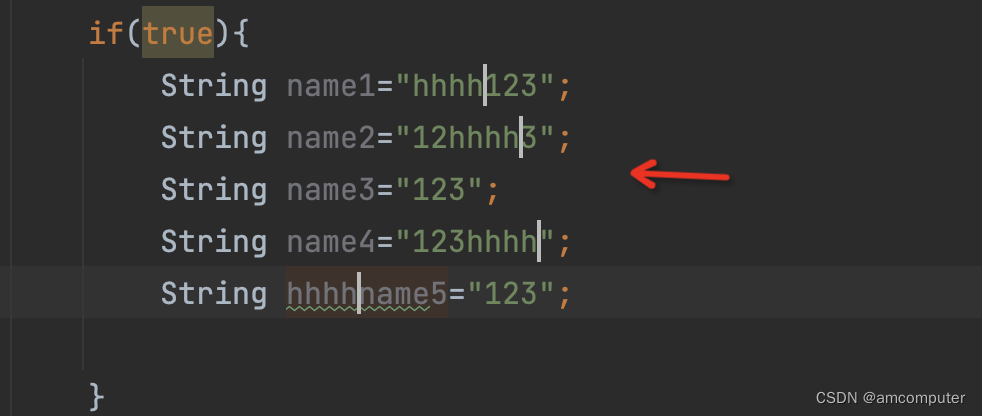
idea同时编辑多行-winmac都支持
1背景介绍 idea编辑器非常强大,其中一个功能非常优秀,很多程序员也非常喜欢用。这个功能能够大大大提高工作效率-------------多行代码同时编辑 2win 2.1方法1 按住alt鼠标左键上/下拖动即可 这样选中多行后,可以直接多行编辑。 优点&a…...

亿级高并发电商项目-- 实战篇 --万达商城项目 十一(编写商品搜索功能、操作商品同步到ES、安装RabbitMQ与Erlang,配置监听队列与消息队列)
👏作者简介:大家好,我是小童,Java开发工程师,CSDN博客博主,Java领域新星创作者 📕系列专栏:前端、Java、Java中间件大全、微信小程序、微信支付、若依框架、Spring全家桶 Ǵ…...

数据结构概述和稀疏数组
数据结构和算法内容介绍 1)算法是程序的灵魂,优秀的程序可以在海量数据计算时,仍然保持高速计算 数据结构和算法概述 1)程序 数据结构算法 2)学好数据结构可以编写出更加漂亮,更加有效率的代码 3&…...
宝塔搭建实战人才求职管理系统adminm前端vue源码(三)
大家好啊,我是测评君,欢迎来到web测评。 上一期给大家分享骑士cms后台admin前端vue在本地运行打包、宝塔发布部署的方式,本期给大家分享,后台adminm移动端后台vue前端怎么在本地运行,打包,实现线上功能更新…...

服务器是干什么用的?
首先,什么是服务器?服务器是提供计算服务器和网络服务的设备。服务器和计算机由CPU、硬盘、内存、系统总线等组成。比如我们访问一个网站,点击这个网站会发出访问请求,服务器会响应服务请求,进行相应的处理,…...

C++ 之结构体与共用体
文章目录参考描述结构体使用(基本)声明初始化先创建后初始化C 11 列表初始化使用(进阶)结构数组声明(拓展)声明及创建声明及初始化匿名结构体细节外部声明与内部声明成员赋值共用体存储空间匿名共用体同化尾…...
)
Java基础知识汇总(良心总结)
1. 前言 本文章是对Java基础知识进行了汇总,方便大家学习。 申明:文章的内容均来自黑马程序员,博主只是将其搬到了CSDN上以共享给大家学习 2. 目录 Day01 Java学习笔记之《开章》 Day02 Java学习笔记之《运算符》 Day03 Java学习笔记之《流程…...
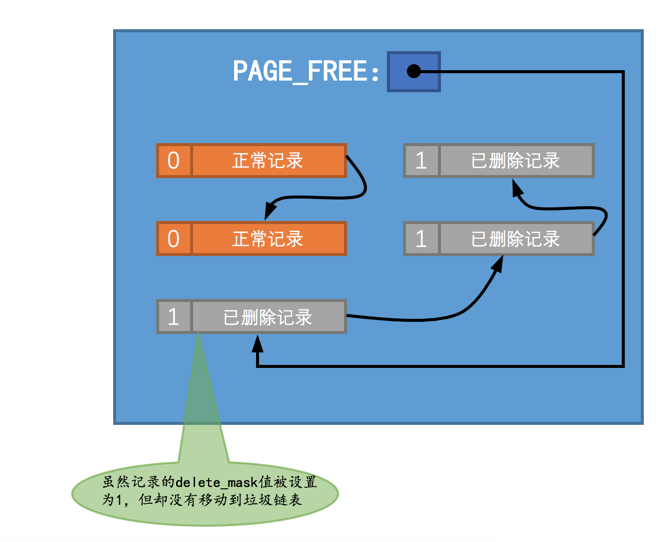
InnoDB之Undo log格式
1. 前言 InnoDB有两大日志模块,分别是redo log和undo log。为了避免磁盘随机写,InnoDB设计了redo log,数据写入时只写缓冲页和redo log,脏页由后台线程异步刷盘,哪怕系统崩溃也能根据redo log恢复数据。但是我们漏了一…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...
