算法导论—SAT、NP、NPC、NP-Hard问题
算法导论—SAT、NP、NP-Hard、NPC问题
- SAT 问题基本定义
- 问题复杂性
- P、NP、NP-Hard、NP-Complete(NPC)
- 证明NP-Hard
- 关系图
- NP问题的概念
- 约化的定义
- NPC问题
- NP-Hard问题
SAT 问题基本定义
-
SAT 问题 (Boolean satisfiability problem, 布尔可满足性问题,SAT):
- 给定布尔 (Boolean) 表达式 (由 AND, OR, NOT, 变量, 和括号构成), 是否存在对变量 TRUE 或 FALSE 的赋值, 使得整个表达式真。
-
SAT 问题 (Propositional satisfiability problem, 命题可满足问题, SAT):
-
给定命题逻辑公式 (propositional formula), 是否可满足 (存在一个模型)。
(¬(x1→¬x2)→x3)→(x1→(x2→x3))(¬(x1 → ¬x2) → x3) → (x1 → (x2 → x3))(¬(x1→¬x2)→x3)→(x1→(x2→x3)) -
任意布尔表达式和命题逻辑公式都可以等价转换为合取范
式。

问题复杂性

P、NP、NP-Hard、NP-Complete(NPC)


证明NP-Hard

P: 能在多项式时间内解决的问题
NP: 不能在多项式时间内解决或不确定能不能在多项式时间内解决,但能在多项式时间验证的问题
NPC: NP完全问题,所有NP问题在多项式时间内都能约化(Reducibility)到它的NP问题,即解决了此NPC问题,所有NP问题也都得到解决。
NP hard:NP难问题,所有NP问题在多项式时间内都能约化(Reducibility)到它的问题(不一定是NP问题)。
关系图
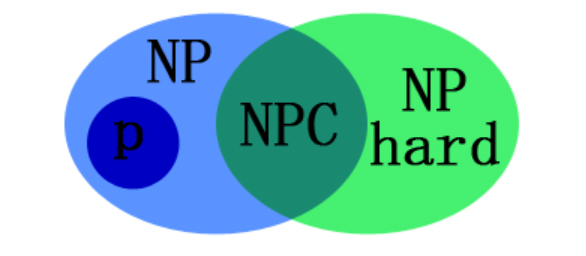
-
P问题属于NP问题,NPC问题属于NP问题。
-
NPC问题同时属于NP hard问题,是NP与NPhard的交集。
NP问题的概念
NP问题不是非P类问题。NP问题是指可以在多项式的时间里验证一个解的问题。NP问题的另一个定义是,可以在多项式的时间里猜出一个解的问题。比方说,我RP很好,在程序中需要枚举时,我可以一猜一个准。现在某人拿到了一个求最短路径的问题,问从起点到终点是否有一条小于100个单位长度的路线。它根据数据画好了图,但怎么也算不出来,于是来问我:你看怎么选条路走得最少?我说,我RP很好,肯定能随便给你指条很短的路出来。然后我就胡乱画了几条线,说就这条吧。那人按我指的这条把权值加起来一看,嘿,神了,路径长度98,比100小。于是答案出来了,存在比100小的路径。别人会问他这题怎么做出来的,他就可以说,因为我找到了一个比100 小的解。在这个题中,找一个解很困难,但验证一个解很容易。验证一个解只需要O(n)的时间复杂度,也就是说我可以花O(n)的时间把我猜的路径的长度加出来。那么,只要我RP好,猜得准,我一定能在多项式的时间里解决这个问题。我猜到的方案总是最优的,不满足题意的方案也不会来骗我去选它。这就是NP问题。当然有不是NP问题的问题,即你猜到了解但是没用,因为你不能在多项式的时间里去验证它。下面我要举的例子是一个经典的例子,它指出了一个目前还没有办法在多项式的时间里验证一个解的问题。很显然,前面所说的Hamilton回路是NP问题,因为验证一条路是否恰好经过了每一个顶点非常容易。但我要把问题换成这样:试问一个图中是否不存在Hamilton回路。这样问题就没法在多项式的时间里进行验证了,因为除非你试过所有的路,否则你不敢断定它“没有Hamilton回路”。
之所以要定义NP问题,是因为通常只有NP问题才可能找到多项式的算法。我们不会指望一个连多项式地验证一个解都不行的问题存在一个解决它的多项式级的算法。相信读者很快明白,信息学中的号称最困难的问题——“NP问题”,实际上是在探讨NP问题与P类问题的关系。
很显然,所有的P类问题都是NP问题。也就是说,能多项式地解决一个问题,必然能多项式地验证一个问题的解——既然正解都出来了,验证任意给定的解也只需要比较一下就可以了。关键是,人们想知道,是否所有的NP问题都是P类问题。我们可以再用集合的观点来说明。如果把所有P类问题归为一个集合P中,把所有 NP问题划进另一个集合NP中,那么,显然有P属于NP。现在,所有对NP问题的研究都集中在一个问题上,即究竟是否有P=NP?通常所谓的“NP问题”,其实就一句话:证明或推翻P=NP。
NP问题一直都是信息学的巅峰。巅峰,意即很引人注目但难以解决。在信息学研究中,这是一个耗费了很多时间和精力也没有解决的终极问题,好比物理学中的大统一和数学中的歌德巴赫猜想等。
目前为止这个问题还“啃不动”。但是,一个总的趋势、一个大方向是有的。人们普遍认为,P=NP不成立,也就是说,多数人相信,存在至少一个不可能有多项式级复杂度的算法的NP问题。人们如此坚信P≠NP是有原因的,就是在研究NP问题的过程中找出了一类非常特殊的NP问题叫做NP-完全问题,也即所谓的 NPC问题。C是英文单词“完全”的第一个字母。正是NPC问题的存在,使人们相信P≠NP。下文将花大量篇幅介绍NPC问题,你从中可以体会到NPC问题使P=NP变得多么不可思议。
约化的定义
为了说明NPC问题,我们先引入一个概念——约化(Reducibility,有的资料上叫“归约”)。
简单地说,一个问题A可以约化为问题B的含义即是,可以用问题B的解法解决问题A,或者说,问题A可以“变成”问题B。《算法导论》上举了这么一个例子。比如说,现在有两个问题:求解一个一元一次方程和求解一个一元二次方程。那么我们说,前者可以约化为后者,意即知道如何解一个一元二次方程那么一定能解出一元一次方程。我们可以写出两个程序分别对应两个问题,那么我们能找到一个“规则”,按照这个规则把解一元一次方程程序的输入数据变一下,用在解一元二次方程的程序上,两个程序总能得到一样的结果。这个规则即是:两个方程的对应项系数不变,一元二次方程的二次项系数为0。按照这个规则把前一个问题转换成后一个问题,两个问题就等价了。同样地,我们可以说,Hamilton回路可以约化为TSP问题(Travelling Salesman Problem,旅行商问题):在Hamilton回路问题中,两点相连即这两点距离为0,两点不直接相连则令其距离为1,于是问题转化为在TSP问题中,是否存在一条长为0的路径。Hamilton回路存在当且仅当TSP问题中存在长为0的回路。
“问题A可约化为问题B”有一个重要的直观意义:B的时间复杂度高于或者等于A的时间复杂度。也就是说,问题A不比问题B难。这很容易理解。既然问题A能用问题B来解决,倘若B的时间复杂度比A的时间复杂度还低了,那A的算法就可以改进为B的算法,两者的时间复杂度还是相同。正如解一元二次方程比解一元一次方程难,因为解决前者的方法可以用来解决后者。
很显然,约化具有一项重要的性质:约化具有传递性。如果问题A可约化为问题B,问题B可约化为问题C,则问题A一定可约化为问题C。这个道理非常简单,就不必阐述了。
现在再来说一下约化的标准概念就不难理解了:如果能找到这样一个变化法则,对任意一个程序A的输入,都能按这个法则变换成程序B的输入,使两程序的输出相同,那么我们说,问题A可约化为问题B。
当然,我们所说的“可约化”是指的可“多项式地”约化(Polynomial-time Reducible),即变换输入的方法是能在多项式的时间里完成的。约化的过程只有用多项式的时间完成才有意义。
好了,从约化的定义中我们看到,一个问题约化为另一个问题,时间复杂度增加了,问题的应用范围也增大了。通过对某些问题的不断约化,我们能够不断寻找复杂度更高,但应用范围更广的算法来代替复杂度虽然低,但只能用于很小的一类问题的算法。再回想前面讲的P和NP问题,联想起约化的传递性,自然地,我们会想问,如果不断地约化上去,不断找到能“通吃”若干小NP问题的一个稍复杂的大NP问题,那么**最后是否有可能找到一个时间复杂度最高,并且能“通吃”所有的 NP问题的这样一个超级NP问题?**答案居然是肯定的。也就是说,存在这样一个NP问题,所有的NP问题都可以约化成它。换句话说,只要解决了这个问题,那么所有的NP问题都解决了。这种问题的存在难以置信,并且更加不可思议的是,这种问题不只一个,它有很多个,它是一类问题。这一类问题就是传说中的NPC 问题,也就是NP-完全问题。NPC问题的出现使整个NP问题的研究得到了飞跃式的发展。我们有理由相信,NPC问题是最复杂的问题。再次回到全文开头,我们可以看到,人们想表达一个问题不存在多项式的高效算法时应该说它“属于NPC问题”。
NPC问题
NPC问题的定义非常简单。同时满足下面两个条件的问题就是NPC问题。
- 首先,它得是一个NP问题;
- 然后,所有的NP问题都可以约化到它。
证明一个问题是 NPC问题也很简单。先证明它至少是一个NP问题,再证明其中一个已知的NPC问题能约化到它(由约化的传递性,则NPC问题定义的第二条也得以满足;至于第一个NPC问题是怎么来的,下文将介绍),这样就可以说它是NPC问题了。
既然所有的NP问题都能约化成NPC问题,那么只要任意一个NPC问题找到了一个多项式的算法,那么所有的NP问题都能用这个算法解决了,NP也就等于P了。因此,给NPC找一个多项式算法太不可思议了。因此,前文才说,“正是NPC问题的存在,使人们相信P≠NP”。我们可以就此直观地理解,NPC问题目前没有多项式的有效算法,只能用指数级甚至阶乘级复杂度的搜索。
NP-Hard问题
NP-Hard问题。NP-Hard问题是这样一种问题,它满足NPC问题定义的第二条(所有的NP问题都可以约化到它)但不一定要满足第一条(就是说,NP-Hard问题要比 NPC问题的范围广)。NP-Hard问题同样难以找到多项式的算法,但它不列入我们的研究范围,因为它不一定是NP问题。即使NPC问题发现了多项式级的算法,NP-Hard问题有可能仍然无法得到多项式级的算法。事实上,由于NP-Hard放宽了限定条件,它将有可能比所有的NPC问题的时间复杂度更高从而更难以解决。
相关文章:

算法导论—SAT、NP、NPC、NP-Hard问题
算法导论—SAT、NP、NP-Hard、NPC问题SAT 问题基本定义问题复杂性P、NP、NP-Hard、NP-Complete(NPC)证明NP-Hard关系图NP问题的概念约化的定义NPC问题NP-Hard问题SAT 问题基本定义 SAT 问题 (Boolean satisfiability problem, 布尔可满足性问题,SAT): 给…...

linux入门---基础指令(上)
这里写目录标题前言ls指令pwd指令cd指令touch指令mkdirrmdirrmman指令cp指令mv指令前言 我们平时使用电脑主要是通过鼠标键盘以及操作系统中自带的图形来对电脑执行相应的命令,比如说我想打开D盘中的cctalk这个文件: 我就可以先用鼠标左键单击这个文件…...
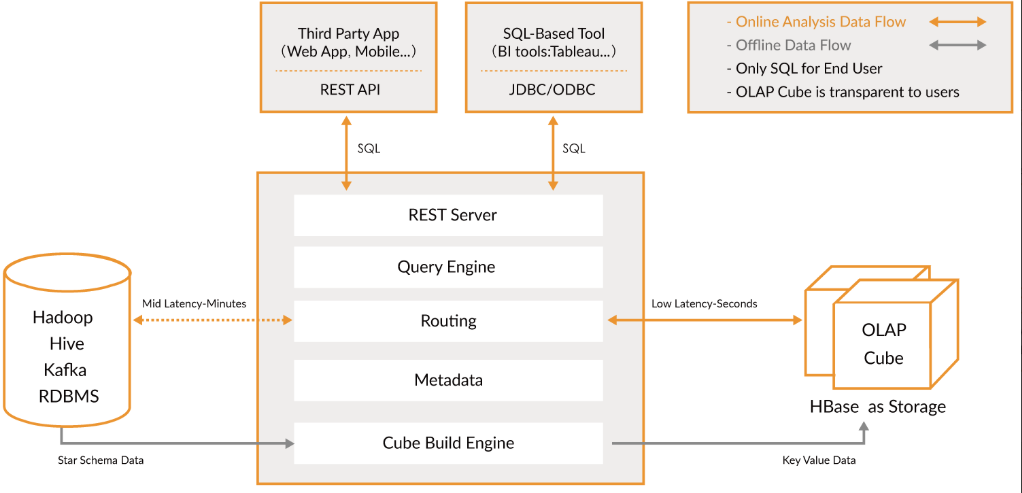
大数据Kylin(一):基础概念和Kylin简介
文章目录 基础概念和Kylin简介 一、OLTP与OLAP 1、OLTP 2、OLAP 3、OLTP与OLAP的关系 二、数据分析模型 1、星型模型 2、雪花模型 …...

推进行业生态发展完善,中国信通院第八批RPA评测工作正式启动
随着人工智能、云计算、大数据等新兴数字技术的高速发展,数字劳动力应用实践步伐加快,以数字生产力、数字创造力为基础的数字经济占比逐年上升。近年来,机器人流程自动化(Robotic Process Automation,RPA)成…...

DOM编程-获取下拉列表选中项的value
<!DOCTYPE html> <html> <head> <meta charset"utf-8"> <title>获取下拉列表选中项的value</title> </head> <body> <script type"text/javascript"> …...

认证服务-----技术点及亮点
大技术Nacos做注册中心把新建的微服务注册到Nacos上去两个步骤 在配置文件中配置应用名称、nacos的发现注册ip地址,端口号在启动类上用EnableDiscoveryClient注解开启注册功能使用Redis存验证码信息加入依赖配置地址和端口号即可直接注入StringRedisTemplate模板类用…...
6个常见的 PHP 安全性攻击
了解常见的PHP应用程序安全威胁,可以确保你的PHP应用程序不受攻击。因此,本文将列出 6个常见的 PHP 安全性攻击,欢迎大家来阅读和学习。 1、SQL注入 SQL注入是一种恶意攻击,用户利用在表单字段输入SQL语句的方式来影响正常的SQL执…...
三大基础排序算法——冒泡排序、选择排序、插入排序
目录前言一、排序简介二、冒泡排序三、选择排序四、插入排序五、对比References前言 在此之前,我们已经介绍了十大排序算法中的:归并排序、快速排序、堆排序(还不知道的小伙伴们可以参考我的 「数据结构与算法」 专栏)࿰…...
负载均衡上传webshell+apache换行解析漏洞
目录一、负载均衡反向代理下的webshell上传1、nginx负载均衡2、负载均衡下webshell上传的四大难点难点一:需要在每一台节点的相同位置上传相同内容的webshell难点二:无法预测下一次请求是哪一台机器去执行难点三:当我们需要上传一些工具时&am…...

【ESP 保姆级教程】玩转emqx数据集成篇③ ——消息重发布
忘记过去,超越自己 ❤️ 博客主页 单片机菜鸟哥,一个野生非专业硬件IOT爱好者 ❤️❤️ 本篇创建记录 2023-02-10 ❤️❤️ 本篇更新记录 2023-02-10 ❤️🎉 欢迎关注 🔎点赞 👍收藏 ⭐️留言📝🙏 此博客均由博主单独编写,不存在任何商业团队运营,如发现错误,请…...
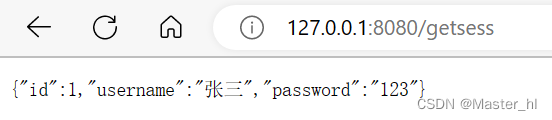
支持分布式部署的主流方式 - Session 持久化到 Redis
1.为什么要将 Session 存储在 Redis 中如果我们不将 Session 存储在 MySQL 或者 Redis 中, 那么做出来的项目就只能支持单机部署, 不支持分布式部署. 因为之前我们只是将 Session 存储在当前电脑的内存里面. 当张三去登录的时候, 将 Session 信息存储在 A 服务器, 这个时候负载…...

计算机网络|第二章 物理层|湖科大课程|从零开始的计网学习——物理层(计网入门就看这篇!)
图片来源于胡科大计算机网络课程,https://www.bilibili.com/video/BV1c4411d7jb?p20&vd_sourcedeb12d86dce7e419744a73045bc66364。文章非盈利商业用途,供博主与大家学习参考,如有侵权,请联系我删除!2.1物理层的基…...
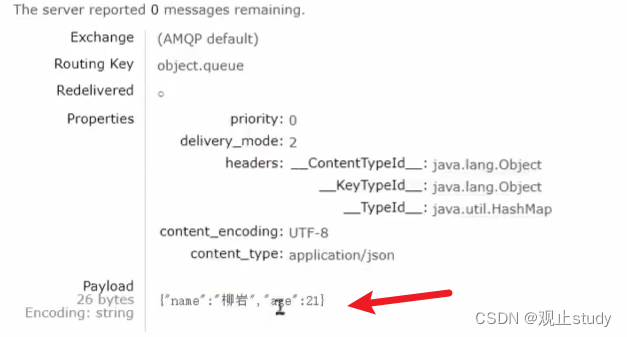
【微服务】RabbitMQSpringAMQP消息队列
🚩本文已收录至专栏:微服务探索之旅 👍希望您能有所收获 一.初识MQ (1) 引入 微服务间通讯有同步和异步两种方式: 同步通讯:就像打电话,可以立即得到响应,但是你却不能跟多个人同时通话。 异…...

jenkins +docker+python接口自动化之docker下安装jenkins(一)
jenkins dockerpython接口自动化之docker下安装jenkins(一) 目录:导读 1、下载jenkins 2、启动jenkins 3、访问jenkins 4.浏览器直接访问http://ip/:8080 5.然后粘贴到输入框中,之后新手入门中先安装默认的插件即可,完成后出…...
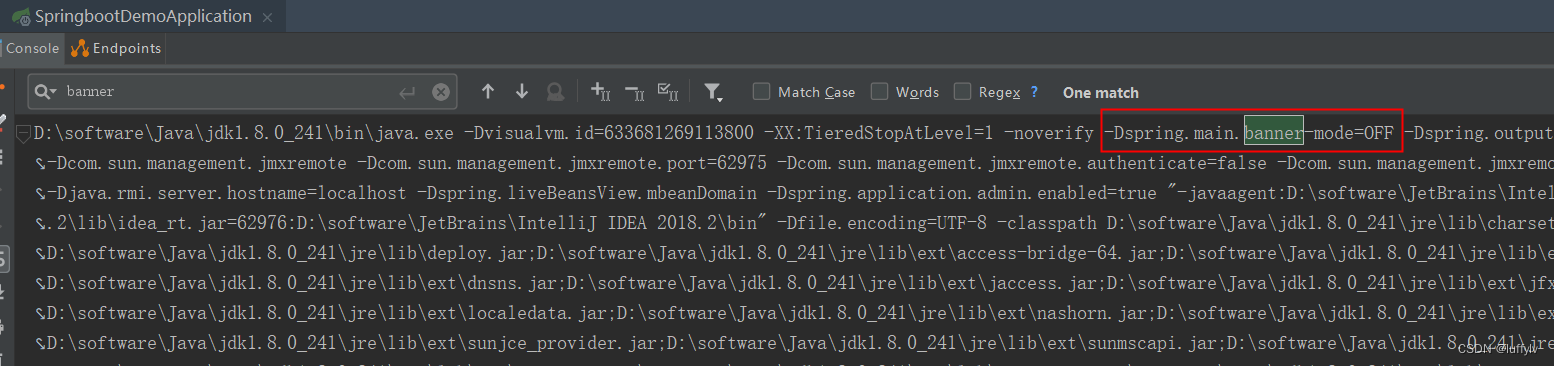
SpringBoot——Banner介绍
一、什么是BannerBanner即横幅标语,我们在启动SpringBoot项目时会将Banner信息打印至控制台。我们可以输出一些图形、SpringBoot版本信息等内容。默认情况下是通过实现类SpringBootBanner输出的Banner内容,默认的输出内容如下。二、自定义Banner如果不想…...

【STL】综述
STL,一文即可知 文章目录一、STL基本知识概述容器二、序列式容器详述数组容器array向量容器vector双端队列容器deque链式容器list正向链容器forward_list二、关联式容器详述红黑树RB-Tree哈希表参考博客😊点此到文末惊喜↩︎ 一、STL基本知识 概述 STL…...

C++中编译的静态库与动态库
1.什么是库库是写好的现有的,成熟的,可以复用的代码。现实中每个程序都要依赖很多基础的底层库,不可能每个人的代码都从零开始,因此库的存在意义非同寻常。本质上来说库是一种可执行代码的二进制形式,可以被操作系统载…...

JS对象到原始值的转换
JS对象到原始值转换的复杂性 主要由于某些对象类型存在不止一种原始值的表示 对象到原始值转换的三种基本算法 在解释三种算法前需要了解toString valueOf这两个方法 toString 返回对象的字符串表示Array类的toString方法会将每个元素转换为字符串,再使用逗号作为…...

深度复盘-重启 etcd 引发的异常
作者信息: 唐聪、王超凡,腾讯云原生产品中心技术专家,负责腾讯云大规模 TKE 集群和 etcd 控制面稳定性、性能和成本优化工作。 王子勇,腾讯云专家级工程师, 腾讯云计算产品技术服务专家团队负责人。 概况 作为当前中国…...
------新特性)
2023年春招热点面试题(一)------新特性
文章目录一、Spring 6.0 新特性二、Spring Boot 3.0 新特性三、JDK 系列 新特性A.**JDK8新特性(2014年初)(LTS版本)**B. **JDK9新特性(2017年9月)**C.**JDK10新特性(2018年3月)**D.*…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...

Axure 下拉框联动
实现选省、选完省之后选对应省份下的市区...

DAY 26 函数专题1
函数定义与参数知识点回顾:1. 函数的定义2. 变量作用域:局部变量和全局变量3. 函数的参数类型:位置参数、默认参数、不定参数4. 传递参数的手段:关键词参数5 题目1:计算圆的面积 任务: 编写一…...
