时间复杂度与空间复杂度的详解
目录
1.时间复杂度
2.时间复杂度计算例题
3.空间复杂度
1.时间复杂度
算法中的基本操作的执行次数,为算法的时间复杂度。
1、用常数1取代运行时间中的所有加法常数。2、在修改后的运行次数函数中,只保留最高阶项。3、如果最高阶项存在且不是1,则去除与这个项目相乘的常数。得到的结果就是大O阶
举例:
// 请计算一下 func1 基本操作执行了多少次?void func1 ( int N ){int count = 0 ;for ( int i = 0 ; i < N ; i ++ ) {for ( int j = 0 ; j < N ; j ++ ) {count ++ ;}}for ( int k = 0 ; k < 2 * N ; k ++ ) {count ++ ;}int M = 10 ;while (( M -- ) > 0 ) {count ++ ;}System . out . println ( count );}
题解:
Func1 执行的基本操作次数 :F(N)=N^2+2*N+10;(1) 用常数1取代运行时间中的所有加法常数。F(N)=N^2+2*N+1;(2) 在修改后的运行次数函数中,只保留最高阶项。F(N)=N^2;=>O(N^2);
通过上面我们会发现大O的渐进表示法去掉了那些对结果影响不大的项,简洁明了的表示出了执行次数。
最坏情况:任意输入规模的最大运行次数 ( 上界 )平均情况:任意输入规模的期望运行次数最好情况:任意输入规模的最小运行次数 ( 下界 )
2.时间复杂度计算例题
例题1:
// 计算 func2 的时间复杂度?void func2 ( int N , int M ) {int count = 0 ;for ( int k = 0 ; k < M ; k ++ ) {count ++ ;}for ( int k = 0 ; k < N ; k ++ ) {count ++ ;}System . out . println ( count );}
答案及分析:
基本操作执行了M+N次,有两个未知数M和N,时间复杂度为 O(N+M)
例题2:
// 计算 func3 的时间复杂度?void func3 ( int N ) {int count = 0 ;for ( int k = 0 ; k < 100 ; k ++ ) {count ++ ;}System . out . println ( count );}
答案及分析:
基本操作执行了100次,通过推导大O阶方法,时间复杂度为 O(1)
例题3:
// 计算 bubbleSort 的时间复杂度?void bubbleSort ( int [] array ) {for ( int end = array . length ; end > 0 ; end -- ) {boolean sorted = true ;for ( int i = 1 ; i < end ; i ++ ) {if ( array [ i - 1 ] > array [ i ]) {Swap ( array , i - 1 , i );sorted = false ;}}if ( sorted == true ) {break ;}}}
答案及分析:
O(N)中N表示问题的规模

F(N)=N*(N-1)=N^2-N;
例题4:
// 计算 binarySearch 的时间复杂度?int binarySearch ( int [] array , int value ) {int begin = 0 ;int end = array . length - 1 ;while ( begin <= end ) {int mid = begin + (( end - begin ) / 2 );if ( array [ mid ] < value )begin = mid + 1 ;else if ( array [ mid ] > value )end = mid - 1 ;elsereturn mid ;}return - 1 ;}
答案及分析:
方法1:
对于不能直接看出的并较复杂的问题,可以采用数学归纳法
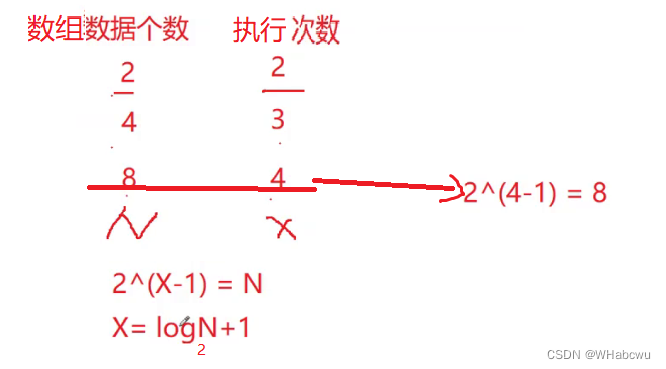
答案:
方法2:

N/(2^x) =1(x为循环的执行次数)
x的解:

例题 5
// 计算阶乘递归 factorial 的时间复杂度?long factorial ( int N ) {return N < 2 ? N : factorial ( N - 1 ) * N ;}
对于不能直接看出的并较复杂的问题,可以采用数学归纳法,但对于递归我们有专门总结的方法。
F(N)=递归的次数*每次递归代码的执行次数
答案及分析:
通过计算分析发现基本操作递归了 N次, 每次递归代码的执行次数为1 时间复杂度为O(N)
例题6:
// 计算斐波那契递归 fifibonacci 的时间复杂度?int fifibonacci ( int N ) {return N < 2 ? N : fifibonacci ( N - 1 ) + fifibonacci ( N - 2 );}
答案及分析:
对于不能直接看出的并较复杂的问题,可以采用数学归纳法(不展开)
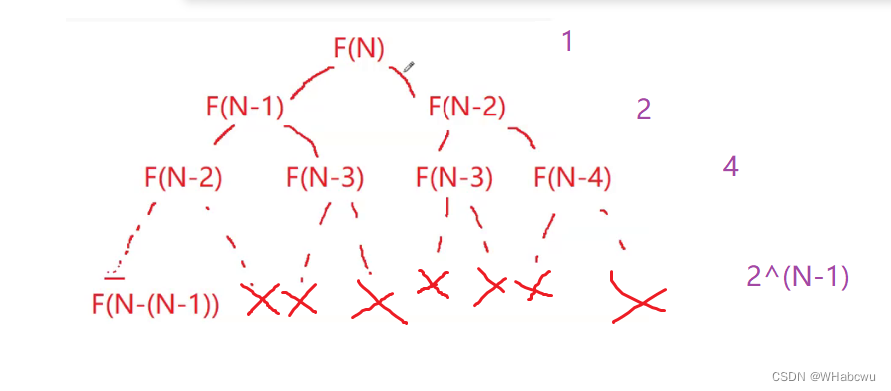
面对这种多递归入口的题,可以使用补全法。
何为补全法?
以F4为例
F(N):
3.空间复杂度
空间复杂度是对一个算法在运行过程中 临时占用存储空间大小的量度 。空间复杂度不是程序占用了多少 bytes 的空 间,因为这个也没太大意义,所以空间复杂度算的是变量的个数
例题1:
// 计算 bubbleSort 的空间复杂度?void bubbleSort ( int [] array ) {for ( int end = array . length ; end > 0 ; end -- ) {boolean sorted = true ;for ( int i = 1 ; i < end ; i ++ ) {if ( array [ i - 1 ] > array [ i ]) {Swap ( array , i - 1 , i );sorted = false ;}}if ( sorted == true ) {break ;}}}
答案及分析:

使用了常数个额外空间,所以空间复杂度为 O(1)
例题2:
// 计算 fifibonacci 的空间复杂度?int [] fifibonacci ( int n ) {long [] fifibArray = new long [ n + 1 ];fifibArray [ 0 ] = 0 ;fifibArray [ 1 ] = 1 ;for ( int i = 2 ; i <= n ; i ++ ) {fifibArray [ i ] = fifibArray [ i - 1 ] + fifibArray [ i - 2 ];}return fifibArray ;}
答案及分析:
动态开辟了N个空间,空间复杂度为 O(N)
例题3:
// 计算阶乘递归 Factorial 的空间复杂度?long factorial ( int N ) {return N < 2 ? N : factorial ( N - 1 ) * N ;}
答案及分析:
递归调用了 N 次,开辟了 N 个栈帧,每个栈帧使用了常数个空间。空间复杂度为 O(N)
以上为我个人的小分享,如有问题,欢迎讨论!!!
都看到这了,不如关注一下,给个免费的赞 ![]()

相关文章:

时间复杂度与空间复杂度的详解
目录 1.时间复杂度 2.时间复杂度计算例题 3.空间复杂度 1.时间复杂度 算法中的基本操作的执行次数,为算法的时间复杂度。 如何表达 时间复杂度? 大O的渐进表示法 实际中我们计算时间复杂度时,我们其实并不一定要计算精确的执行次数…...
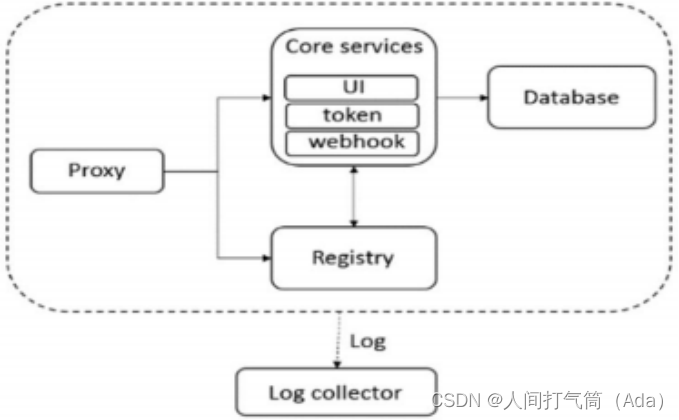
每日一学:什么是 Harbor ?
目录 什么是 Harbor ? 一、Harbor 的优势 二、Harbor 架构构成 三、Core services 这是 Harbor 的核心功能 什么是 Harbor ? Harbor 是 VMware 公司开源的企业级 Docker Registry 项目,其目标是帮助用户迅速搭建一个企业级的 Docker Reg…...
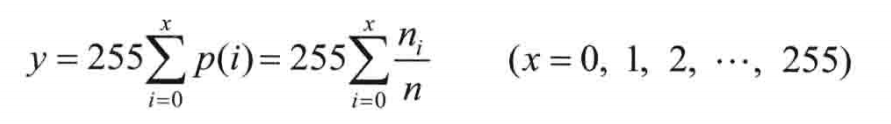
灰度均衡变换之c++实现(qt + 不调包)
1.基本原理 灰度均衡是以累计分布函数变换为基础的直方图修正法,它可以产生一副灰度级分布概率均匀的图像。也就是说,经过灰度均衡后的图像在没一级灰度上像素点的数量相差不大。公式见下图,为灰度值为x的像素点的个数,n为总像素点…...

flink1.17 自定义trigger ContinuousEventTimeTrigger
在 ContinuousEventTimeTrigger 的基础上新增了timeout,如果超时后窗口都没关闭,那么就硬输出一波,避免间断数据,留存窗口太久. ContinuousEventTimeTrigger ContinuousEventTimeTrigger连续事件时间触发器与ContinuousProcessingTimeTrigger连续处理时间触发器,指定一个固定…...

AIGC:【LLM(五)】——Faiss:高效的大规模相似度检索库
文章目录 一.简介1.1 什么是Faiss1.2 Faiss的安装 二.Faiss检索流程2.1 构建向量库2.2 构建索引2.3 top-k检索 三.Faiss构建索引的多种方式3.1 Flat :暴力检索3.2 IVFx Flat :倒排暴力检索3.3 IVFxPQy 倒排乘积量化3.4 LSH 局部敏感哈希3.5 HNSWx 一.简介…...
-[记忆的类型Ⅱ])
自然语言处理从入门到应用——LangChain:记忆(Memory)-[记忆的类型Ⅱ]
分类目录:《自然语言处理从入门到应用》总目录 对话知识图谱记忆(Conversation Knowledge Graph Memory) 这种类型的记忆使用知识图谱来重建记忆: from langchain.memory import ConversationKGMemory from langchain.llms impo…...

桥接模式-java实现
桥接模式 桥接模式的本质,是解决一个基类,存在多个扩展维度的的问题。 比如一个图形基类,从颜色方面扩展和从形状上扩展,我们都需要这两个维度进行扩展,这就意味着,我们需要创建一个图形子类的同时&#x…...

Linux systemd管理常用的几个小案例
systemd是目前Linux系统上主要的系统守护进程管理工具,配置文件要以.service结尾且放到 /usr/lib/systemd/system/目录下面 1、systemd管理ElasticSearch [Unit] DescriptionElasticsearch Service[Service] Typeforking Userelastic Groupelastic ExecStart/home…...
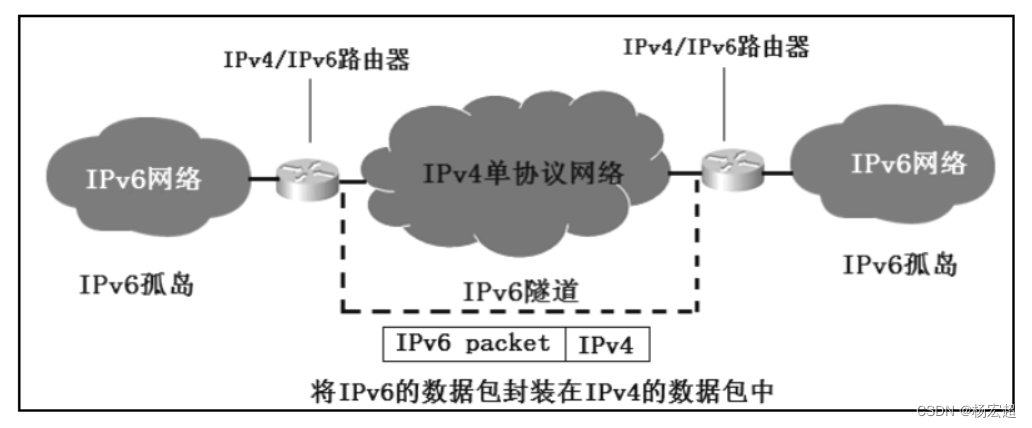
38、IPv6过渡技术
本节内容作为IPv6相关知识的最后一节内容,同时也作为我们本专栏网络层知识的最后一节内容,主要介绍从IPv4地址到IPv6地址过渡的相关技术。在这里我们只学习各类考试中常考的三种技术。 IPv4向IPv6的过渡 在前面的知识中,我们学习到了两种IP地…...

HMMER-序列分析软件介绍
HMMER是一个软件包,它提供了制作蛋白质和DNA序列域家族概率模型的工具,称为轮廓隐马尔可夫模型、轮廓HMM或仅轮廓,并使用这些轮廓来注释新序列、搜索序列数据库以寻找其他同源物,以及进行深度多重序列比对。HMMER是已知蛋白质和DN…...
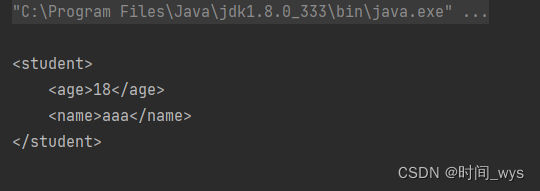
【项目学习1】如何将java对象转化为XML字符串
如何将java对象转化为XML字符串 将java对象转化为XML字符串,可以使用Java的XML操作库JAXB,具体操作步骤如下: 主要分为以下几步: 1、创建JAXBContext对象,用于映射Java类和XML。 JAXBContext jaxbContext JAXBConte…...

nginx负载均衡
负载均衡:反向代理来实现 正向代理的配置方法。 1、NGINX的七层代理和四层代理: 七层是最常用的反向代理方式,只能配置在nginx配置文件的http模块。而且配置方法名称:upstream 模块,不能写在server中,也…...
【毕业项目】自主设计HTTP
博客介绍:运用之前学过的各种知识 自己独立做出一个HTTP服务器 自主设计WEB服务器 背景目标描述技术特点项目定位开发环境WWW介绍 网络协议栈介绍网络协议栈整体网络协议栈细节与http相关的重要协议 HTTP背景知识补充特点uri & url & urn网址url HTTP请求和…...
关于安卓jar包修改并且重新发布
背景: 对于某些jar包,其内部是存在bug的,解决的方法无外乎就有以下几种方法: (1)通过反射,修改其赋值逻辑 (2)通过继承,重写其方法 (3࿰…...

Java课题笔记~ AspectJ 对 AOP 的实现(掌握)
AspectJ 对 AOP 的实现(掌握) 对于 AOP 这种编程思想,很多框架都进行了实现。Spring 就是其中之一,可以完成面向切面编程。然而,AspectJ 也实现了 AOP 的功能,且其实现方式更为简捷,使用更为方便,而且还支…...
npm 报错 cb() never called!
不知道有没有跟我一样的情况,在使用npm i的时候一直报错:cb() never called! 换了很多个node版本,还是不行,无法解决这个问题 百度也只是让降低node版本请缓存,gpt给出的解决方案也是同样的 但是缓存清过很多次了&a…...

finally有什么作用以及常用场景
在Java中,finally是一个关键字,用于定义一个代码块,该代码块中的代码无论是否发生异常都会被执行。finally块通常用于确保在程序执行过程中资源的释放和清理。 使用场景: 1. 资源释放:finally块经常用于释放打开的资…...

Python web实战之Django URL路由详解
概要 技术栈:Python、Django、Web开发、URL路由 Django是一种流行的Web应用程序框架,它采用了与其他主流框架类似的URL路由机制。URL路由是指将传入的URL请求映射到相应的视图函数或处理程序的过程。 什么是URL路由? URL路由是Web开发中非常…...
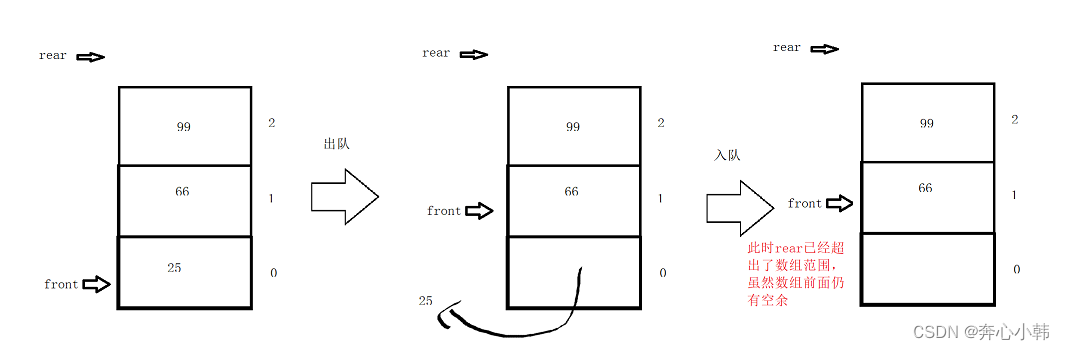
10-数据结构-队列(C语言)
队列 目录 目录 队列 一、队列基础知识 二、队列的基本操作 1.顺序存储 编辑 (1)顺序存储 (2)初始化及队空队满 (3)入队 (4)出队 (5)打印队列 &…...

面试之快速学习C++11 - 右值 移动构造 std::move
C11右值引用 字面意思,以引用传递的方式使用c右值左值和右值,左值是lvalue loactor value 存储在内存中,有明确存储地址的数据, 右值rvalue read value , 指的是那些可以提供数据值的数据(不一定可以寻址,…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...

【学习笔记】erase 删除顺序迭代器后迭代器失效的解决方案
目录 使用 erase 返回值继续迭代使用索引进行遍历 我们知道类似 vector 的顺序迭代器被删除后,迭代器会失效,因为顺序迭代器在内存中是连续存储的,元素删除后,后续元素会前移。 但一些场景中,我们又需要在执行删除操作…...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...

给网站添加live2d看板娘
给网站添加live2d看板娘 参考文献: stevenjoezhang/live2d-widget: 把萌萌哒的看板娘抱回家 (ノ≧∇≦)ノ | Live2D widget for web platformEikanya/Live2d-model: Live2d model collectionzenghongtu/live2d-model-assets 前言 网站环境如下,文章也主…...

什么是VR全景技术
VR全景技术,全称为虚拟现实全景技术,是通过计算机图像模拟生成三维空间中的虚拟世界,使用户能够在该虚拟世界中进行全方位、无死角的观察和交互的技术。VR全景技术模拟人在真实空间中的视觉体验,结合图文、3D、音视频等多媒体元素…...
