自抗扰控制ADRC之微分器TD
目录
前言
1 全程快速微分器
1.1仿真分析
1.2仿真模型
1.3仿真结果
1.4结论
2 Levant微分器
2.1仿真分析
2.2仿真模型
2.3仿真结果
3.总结
前言
工程上信号的微分是难以得到的,所以本文采用微分器实现带有噪声的信号及其微分信号提取,从而实现无需测量速度信号的控制。并且结合控制对象简单的用PID进行控制,即TD微分器+PID控制。
1 全程快速微分器
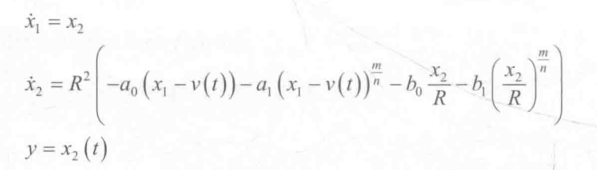
其中:
①x1为带有噪音的信号,也是TD的第一个状态变量,同理x2为信号的微分;
②R>0;a0、a1、b0、b1≥0;m和n为大于0的奇数,且m<n;
③当a1=b1=0时,上述微分器为线性微分器。
1.1仿真分析
取R=1/0.05, a=0.1,b=0.1,已知输入信号为v(t)= sint,并且带有噪声信号,噪声的幅值为0.05,采用连续的全程快速微分器提取信号及信号的微分。
1.2仿真模型

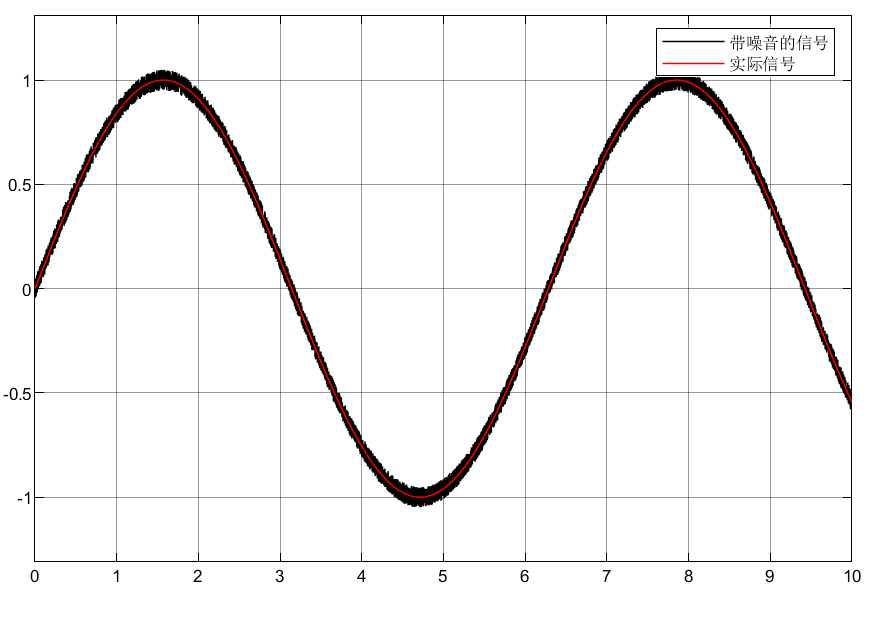
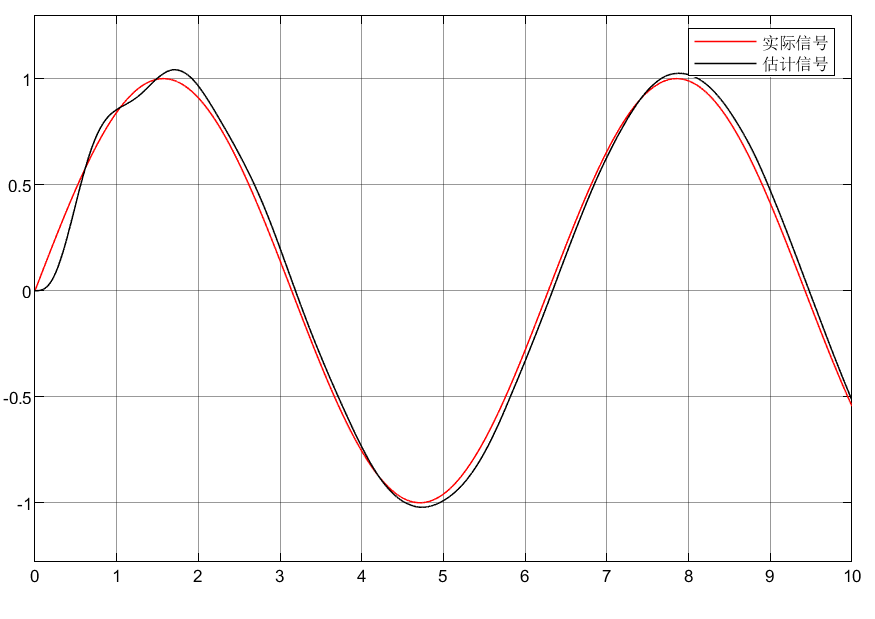
1.3仿真结果
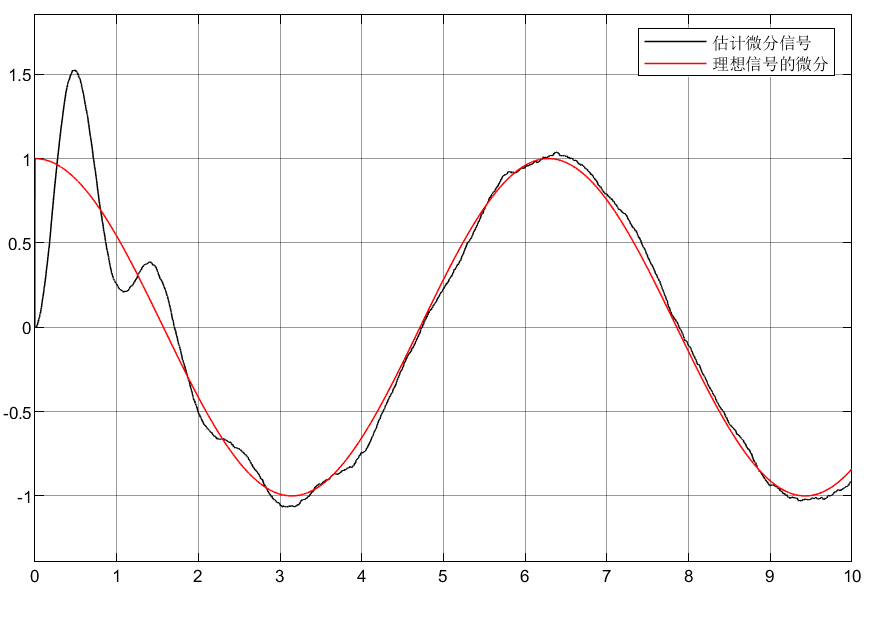
1.4结论
①可以看到虽然和实际信息有些偏差,但是估计的效果还算可以。
②对于a1、b1≠0的非线性微分器好像调节效果和线性差不多,即a1、b1、m、n调节没效果?
③位移信号可以调节的很好,但是会牺牲微分信号。
④仿真注意:(1)噪声模块的采样时间为继承采样时间;(2)simulink仿真求解步长为定步长0.001
2 Levant微分器
微分器需要对信号的测量误差和输入噪声具有鲁棒性,而Levant微分器是基于滑模奇数的非线性微分器,其二阶微分器表达形式为:
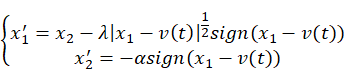

对于Lipschitz的定义部分可参考下面博客的3.1部分:
基于LMI的非线性混沌系统滑模控制_Mr. 邹的博客-CSDN博客
注:虽然这类微分器具有滑模控制的鲁棒性,但是对于Levant微分器,需要事先知道输入信号v(t)导数的Lipschitz常数上界,才能设计微分器参数,这就限制了输入信号的类型。而且,对于这种微分器,抖振现象不可避免。
2.1仿真分析
同样取上述的噪音信号及其微分进行估计,选取参数:
①Lipschitz的常数上界为1,即C = 1,所以α > 1,取α = 18;
②λ > 4*C*(α+C)/(α-C),得λ≥4.4706,所以取λ = 6。
2.2仿真模型
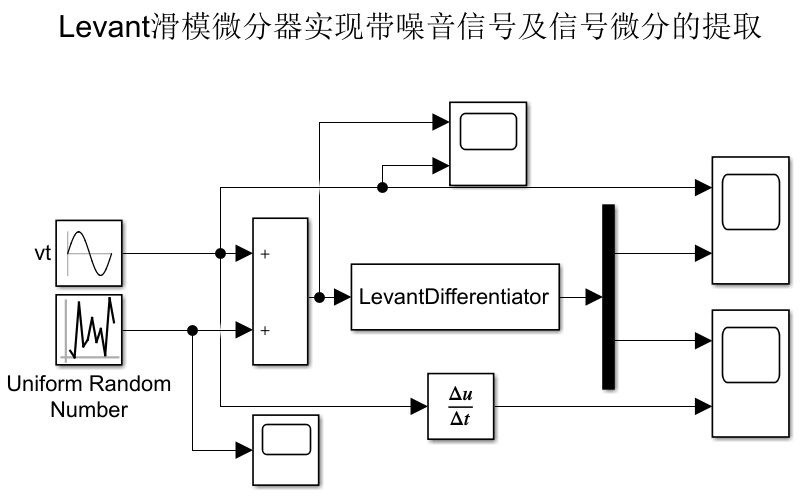
2.3仿真结果
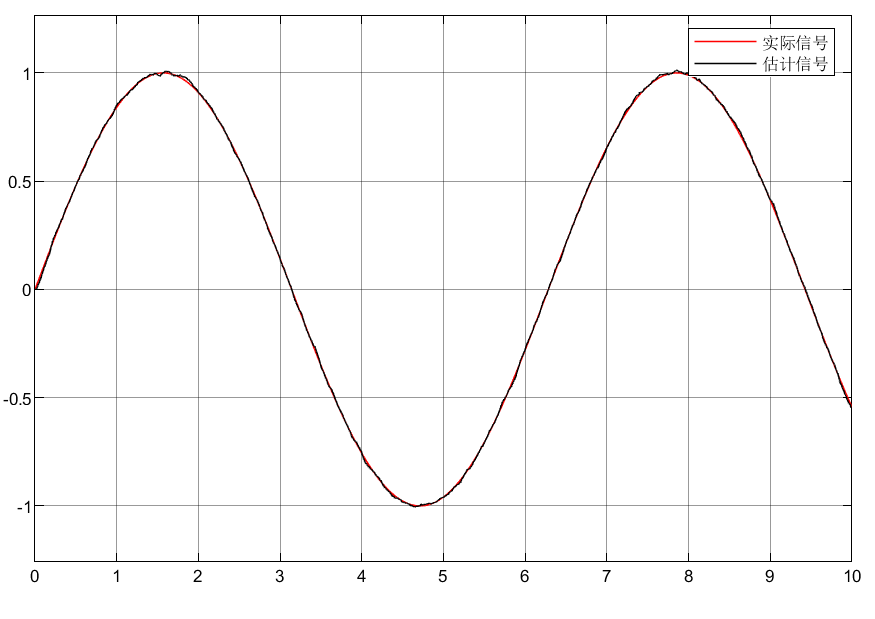
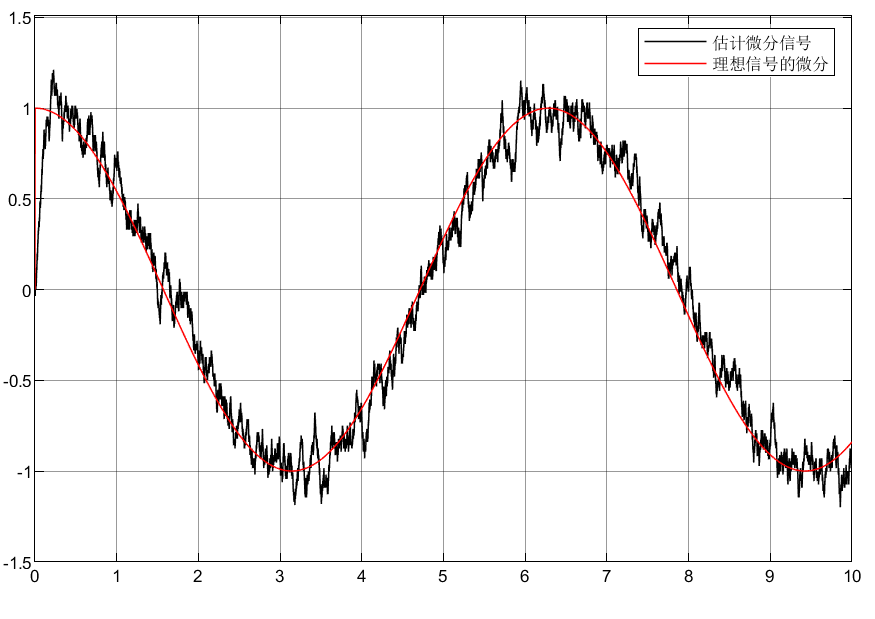
3.总结
①可以看到两种微分器都能将实现带噪声信号的估计,虽然有一定的误差
②信号的微分估计的稍差一些
③注意仿真时噪声模块的采样时间设定为继承采样时间:-1;且simulink设定为定步长0.001的求解器。
相关文章:

自抗扰控制ADRC之微分器TD
目录 前言 1 全程快速微分器 1.1仿真分析 1.2仿真模型 1.3仿真结果 1.4结论 2 Levant微分器 2.1仿真分析 2.2仿真模型 2.3仿真结果 3.总结 前言 工程上信号的微分是难以得到的,所以本文采用微分器实现带有噪声的信号及其微分信号提取,从而实现…...

链表学习之复制含随机指针的链表
链表解题技巧 额外的数据结构(哈希表);快慢指针;虚拟头节点; 复制含随机指针的链表 该链表节点的结构如下: class ListRandomNode { public:ListRandomNode() : val(0), next(nullptr), random(nullptr…...
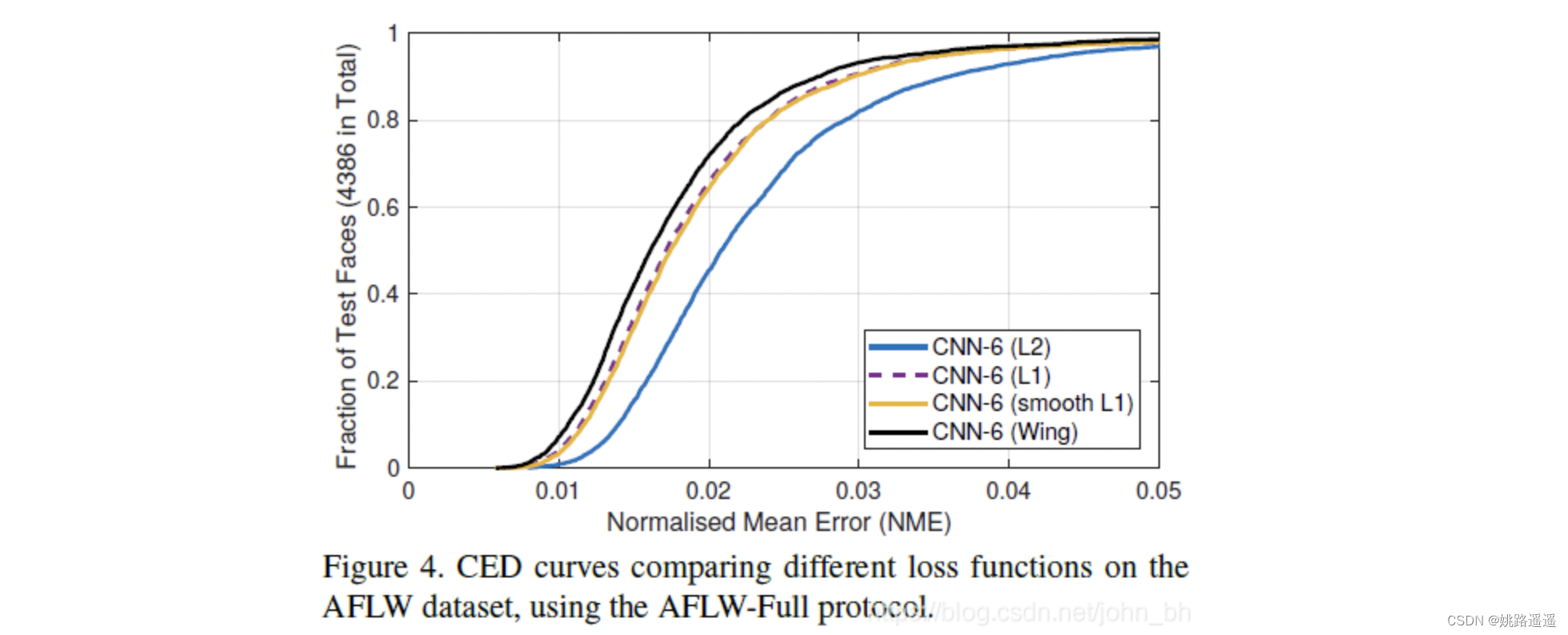
【人脸检测】Yolov5Face:优秀的one-stage人脸检测算法
论文题目:《YOLO5Face: Why Reinventing a Face Detector》 论文地址:https://arxiv.org/pdf/2105.12931.pdf 代码地址:https://github.com/deepcam-cn/yolov5-face 1.简介 近年来,CNN在人脸检测方面已经得到广泛的应用。但是许多…...
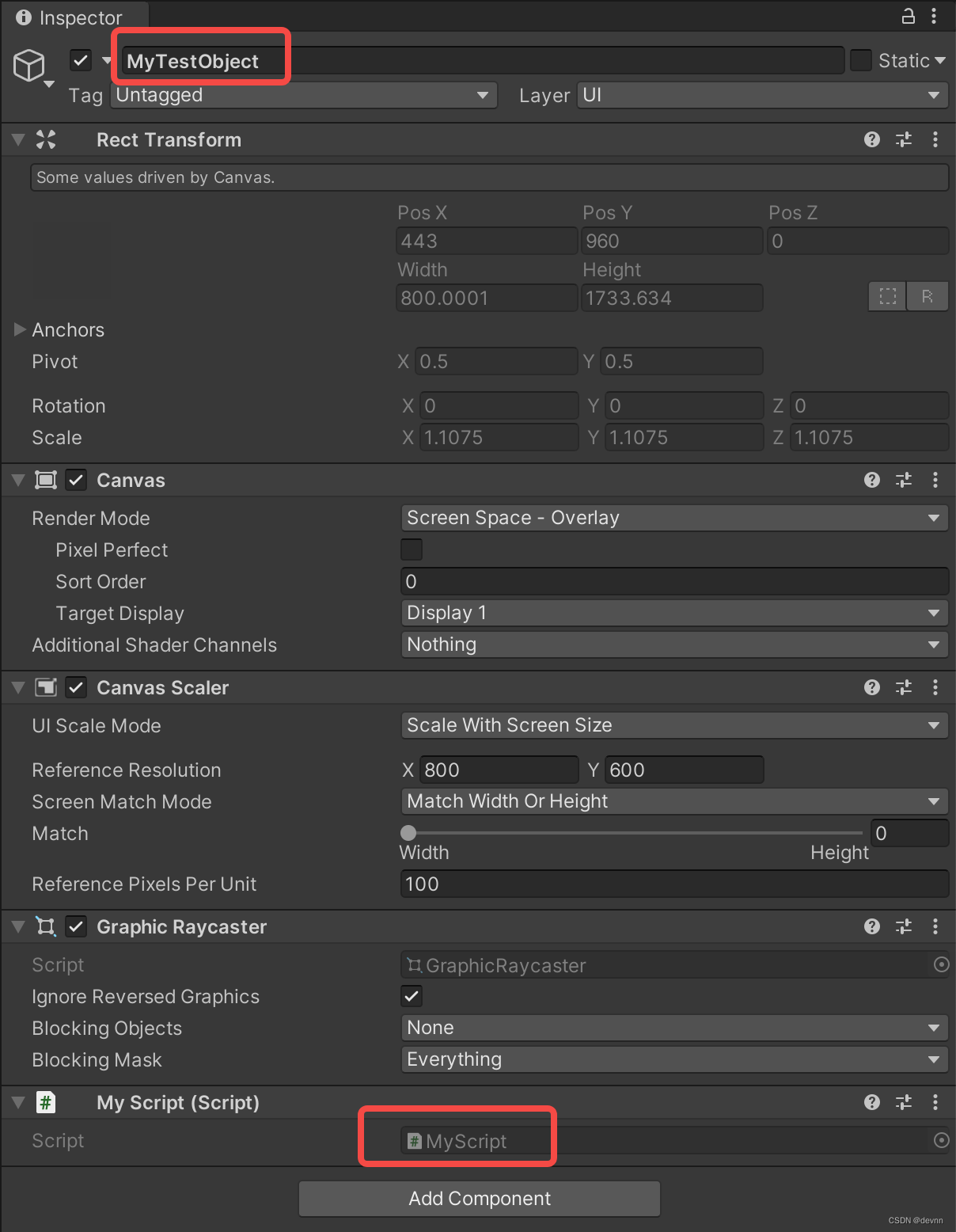
【Unity3d】Unity与Android之间通信
在unity开发或者sdk开发经常遇到unity与移动端原生层之间进行通信,这里把它们之间通信做一个整理。 关于Unity与iOS之间通信,参考【Unity3d】Unity与iOS之间通信 Unity(c#)调用Android (一)、编写Java代码 实际上,任何已经存在的Java代码…...
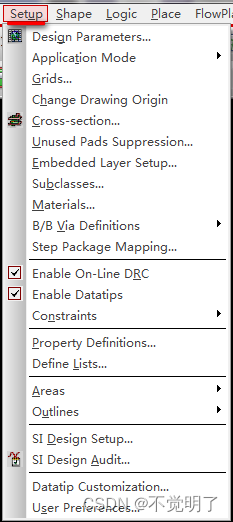
Allegro如何更改DRC尺寸大小操作指导
Allegro如何更改DRC尺寸大小操作指导 在做PCB设计的时候,DRC可以辅助设计,有的时候DRC的尺寸过大会影响视觉,Allegro支持将DRC的尺寸变小或者改大 如下图,DRC尺寸过大 如何改小,具体操作如下 点击Setup选择Design Parameters...

Mongodb WT_PANIC: WiredTiger library panic
文章目录故障现象排查过程1.查看Log2.同步恢复数据故障现象 周五突然收到Mongo实例莫名奇妙挂了告警,一般都是RS复制集架构模式(5节点),查看此实例角色为SECONDAR,挂了暂时不影响线上业务,但还是需要尽快修…...
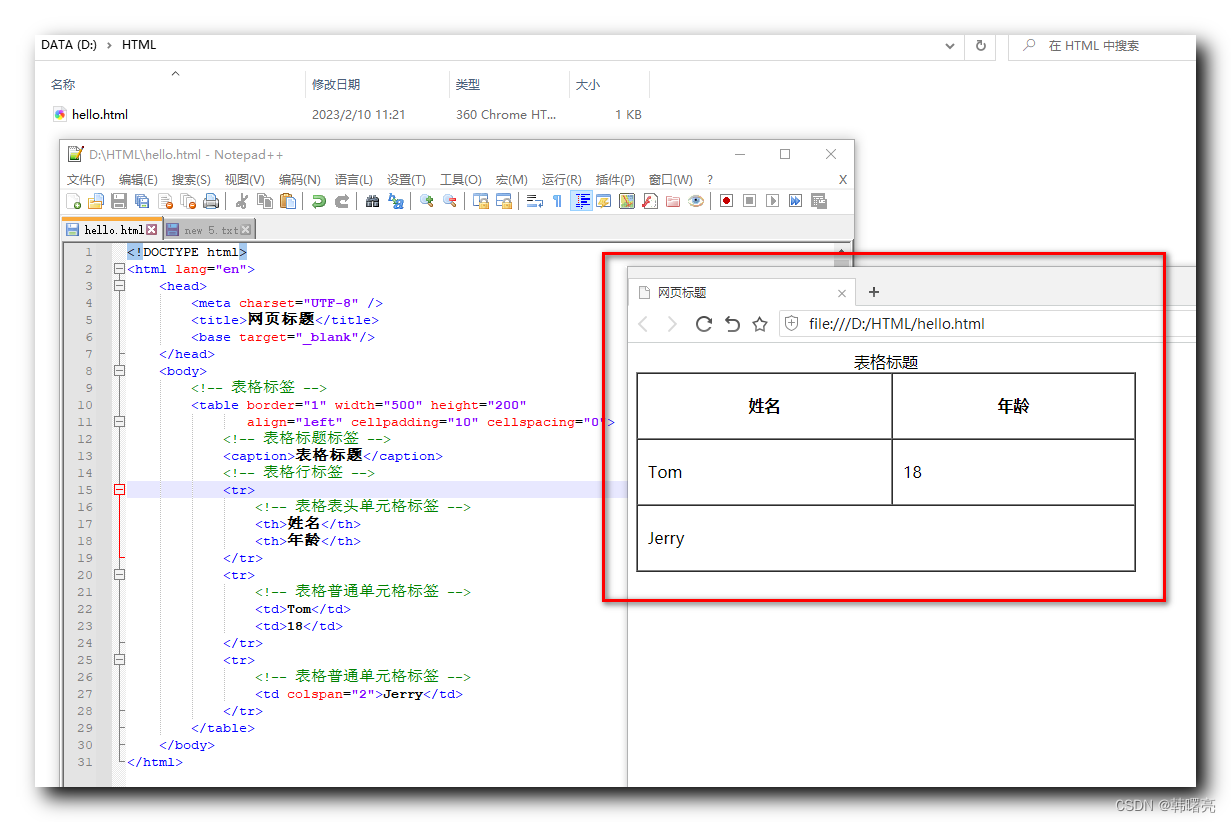
【HTML】HTML 表格总结 ★★★ ( 表格标签 | 行标签 | 单元格标签 | 表格标签属性 | 表头单元格标签 | 表格标题标签 | 合并单元格 )
文章目录一、表格标签组成 ( 表格标签 | 行标签 | 单元格标签 )二、table 表格属性 ( border 属性 | align 属性 | width 属性 | height 属性 )三、表头单元格标签四、表格标题标签五、合并单元格1、合并单元格方式2、合并单元格顺序3、合并单元格流程六、合并单元格示例1、原始…...

linux013之文件和目录的权限管理
用户、组、文件目录的关系: 简介:用户和组关联,组合文件目录关联,这样就实现了用户对文件的权限管理。首先来看一下,一个文件或目录的权限是怎么查看的,ls -l, 如下,这个信息怎么看呢…...
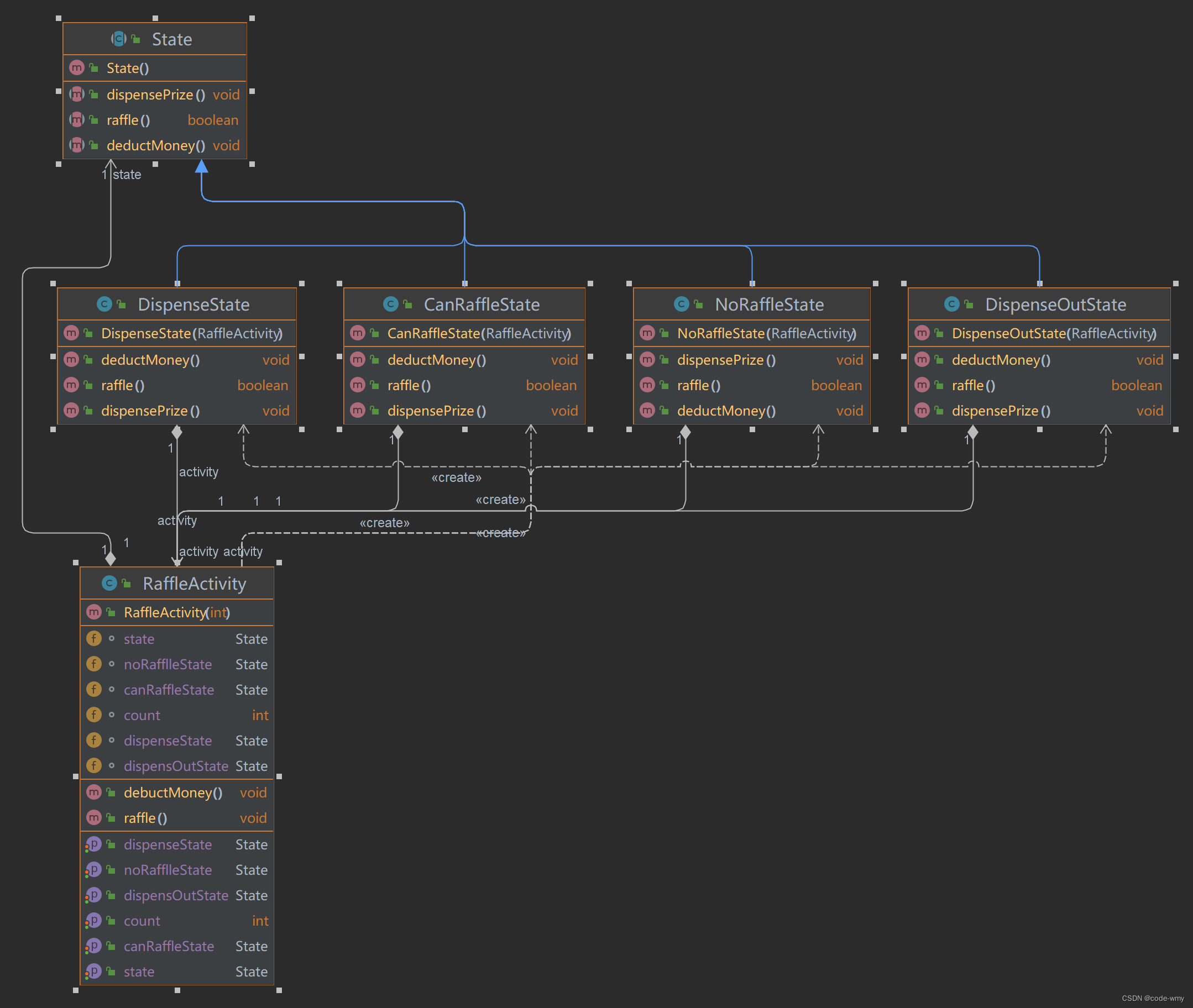
设计模式之状态模式
什么是状态模式 状态模式是指允许一个对象在其内部状态改变时改变他的行为,对象看起来似乎改变了整个类。 状态模式将一个对象在不同状态下的不同行为封装在一个个状态类中,通过设置不同的状态对象可以让环境对象拥有不同的行为,而状…...

XQuery 选择 和 过滤
XML实例文档 我们将在下面的例子中继续使用这个 "books.xml" 文档(和上面的章节所使用的 XML 文件相同)。 在您的浏览器中查看 "books.xml" 文件。 选择和过滤元素 正如在前面的章节所看到的,我们使用路径表达式或 FL…...

室友打了一把王者的时间,我理清楚了grep,find,管道|,xargs的区别与联系,用的时候不知道为什么要这样用
目录 问题引入 find和grep的基本区别 xargs命令 Linux命令的标准输入 vs 命令行参数 举例总结 问题引入 在自己做项目的过程中,想使用linux命令统计下一个目录下html文件的数量,在思考应该使用grep还是find去配合wc指令统计文件数量,后来…...
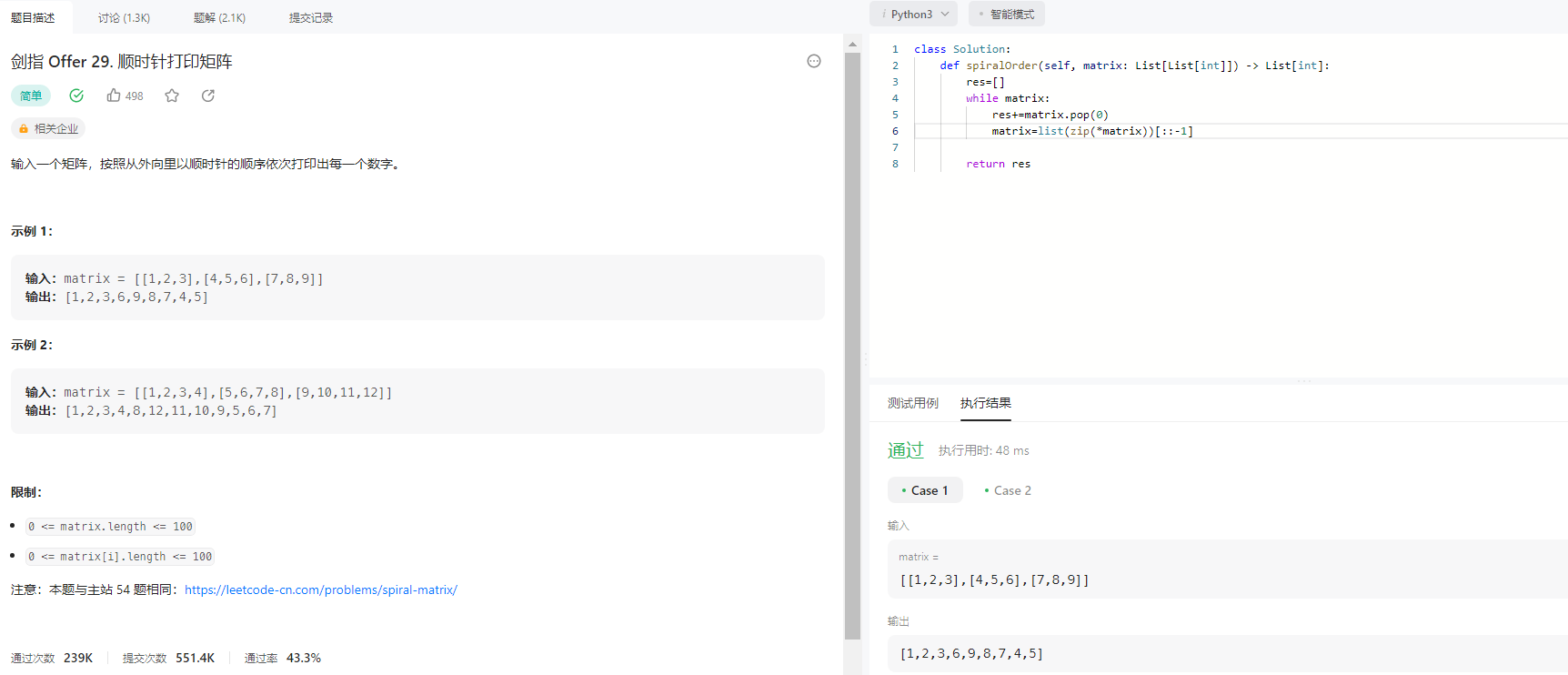
python 刷题时常见的函数
collections.OrderedDict 1. move_to_end() move_to_end() 函数可以将指定的键值对移动到最前面或者最后面,即最左边或最右边 。 2. popitem() popitem()可以完成元素的删除操作,有一个可选参数last(默认为True),…...

Python之列表推导式和列表排序
Python中的列表推导式,是小编比较喜欢的一种,他能大大减少你的代码量来得到你想要的结果,下面说说列表中常用的几种推导式 列表排序 Python开发中会经常用到排序操作,这里提供两种方式供大家参考,对象的sort()方法和…...

力扣(LeetCode)240. 搜索二维矩阵 II(C++)
题目描述 枚举 枚举整个矩阵,找到等于 target 的元素,则 return true ,否则 return false。 class Solution { public:bool searchMatrix(vector<vector<int>>& matrix, int target) {int n matrix.size(), m matrix[0]…...

golang defer
文章目录延迟函数的参数在defer语句出现时就已经确定下来了延迟函数没有入参时,延迟函数体内的变量会受到影响延迟函数 *可以* 修改主函数的 *具名* 返回值延迟函数 *无法* 修改主函数的 *匿名* 返回值defer会把声明的 延迟函数以及 函数的入参放到栈上,…...
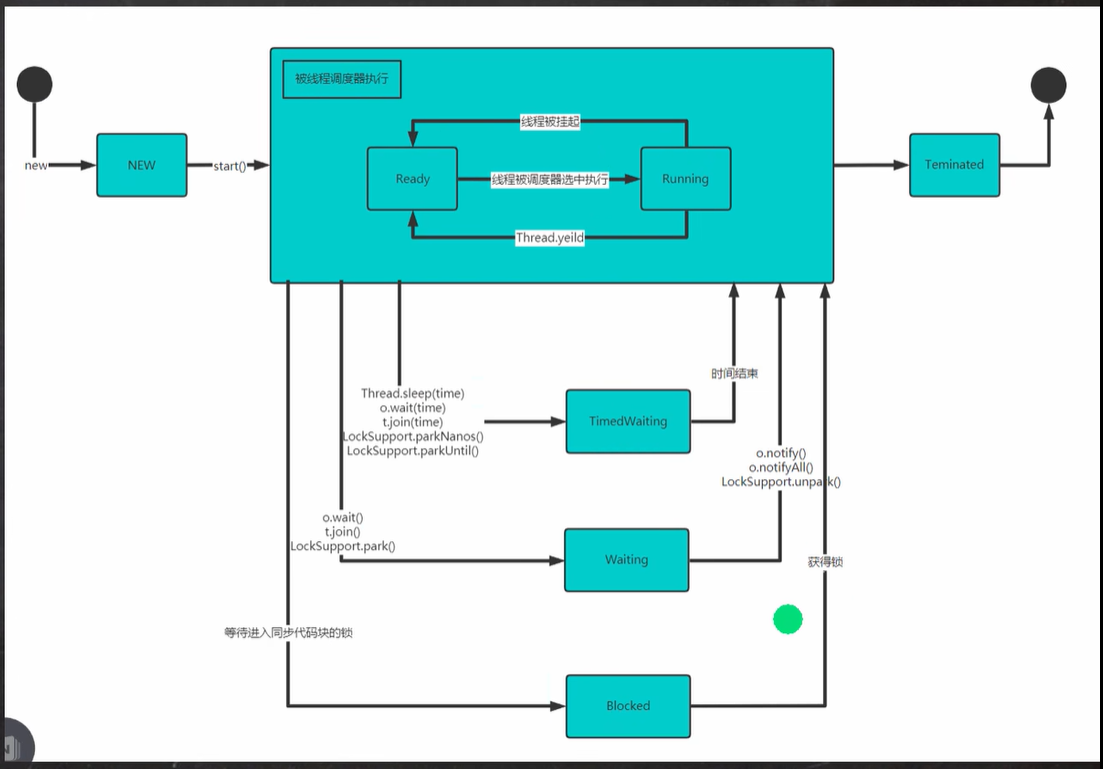
【Java】线程的死锁和释放锁
线程死锁是线程同步的时候可能出现的一种问题 文章目录1. 线程的死锁1.1 基本介绍1.2 应用案例2. 释放锁2.1 下面的操作会释放锁2.2 下面的操作不会释放锁1. 线程的死锁 1.1 基本介绍 多个线程都占用了对方的锁资源,但不肯相让,导致了死锁,…...
如何使用断点续传上传大文件
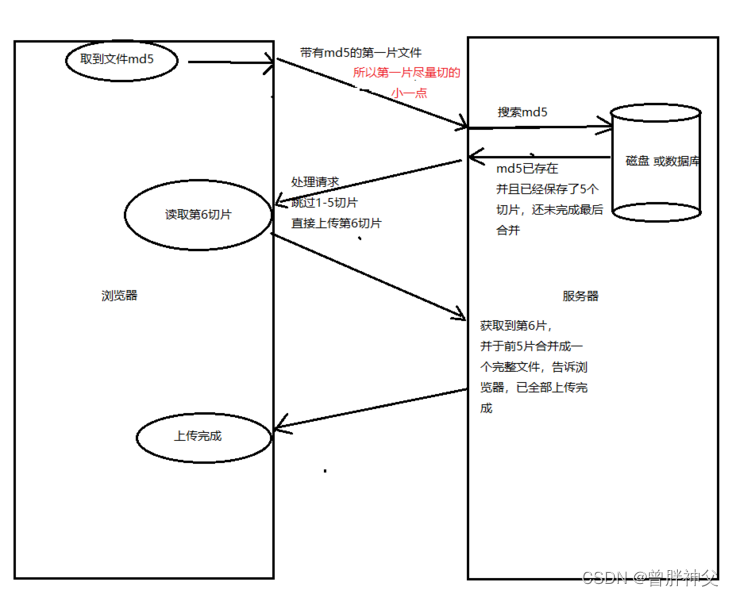
概念 大文件上传的需求介绍 不管怎样简单的需求,在量级达到一定层次时,都会变得异常复杂。 文件上传简单,文件变大就复杂 上传大文件时,以下几个变量会影响我们的用户体验 服务器处理数据的能力请求超时网络波动 上传时间会变长…...
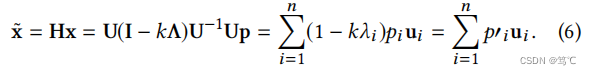
【图神经网络】图拉普拉斯滤波器如何实现全通、低通、高通滤波
【图神经网络】图拉普拉斯滤波器如何实现全通、低通、高通滤波 文章目录【图神经网络】图拉普拉斯滤波器如何实现全通、低通、高通滤波1. 前言2. 符号说明3. 三种滤波3.1 全通滤波3.2 低通滤波3.2.1 平滑信号分析3.2.2 广义拉普拉斯平滑滤波器3.3 高通滤波4. 总结1. 前言 GCN&…...

python操作mysql数据库详解
使用Python操作MySQL数据库 MySQL是一种关系型数据库管理系统,它可以用来存储和管理大量的数据。之前介绍了大部分主流数据库,今天将介绍如何使用Python来操作MySQL数据库。 安装MySQL 首先,我们需要安装MySQL服务器,可以从MyS…...
netty群聊系统
1设计思路:启动一个服务端,多个客户端第一个客户端启动时,会告诉服务器上线了第二个客户端启动时,告诉服务器上线,并且通知第一个启动的客户端第三个客户端启动时,告诉服务器上线,并且通知第一个…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

uniapp 小程序 学习(一)
利用Hbuilder 创建项目 运行到内置浏览器看效果 下载微信小程序 安装到Hbuilder 下载地址 :开发者工具默认安装 设置服务端口号 在Hbuilder中设置微信小程序 配置 找到运行设置,将微信开发者工具放入到Hbuilder中, 打开后出现 如下 bug 解…...

CVPR2025重磅突破:AnomalyAny框架实现单样本生成逼真异常数据,破解视觉检测瓶颈!
本文介绍了一种名为AnomalyAny的创新框架,该方法利用Stable Diffusion的强大生成能力,仅需单个正常样本和文本描述,即可生成逼真且多样化的异常样本,有效解决了视觉异常检测中异常样本稀缺的难题,为工业质检、医疗影像…...

【把数组变成一棵树】有序数组秒变平衡BST,原来可以这么优雅!
【把数组变成一棵树】有序数组秒变平衡BST,原来可以这么优雅! 🌱 前言:一棵树的浪漫,从数组开始说起 程序员的世界里,数组是最常见的基本结构之一,几乎每种语言、每种算法都少不了它。可你有没有想过,一组看似“线性排列”的有序数组,竟然可以**“长”成一棵平衡的二…...

跨平台商品数据接口的标准化与规范化发展路径:淘宝京东拼多多的最新实践
在电商行业蓬勃发展的当下,多平台运营已成为众多商家的必然选择。然而,不同电商平台在商品数据接口方面存在差异,导致商家在跨平台运营时面临诸多挑战,如数据对接困难、运营效率低下、用户体验不一致等。跨平台商品数据接口的标准…...

【java面试】微服务篇
【java面试】微服务篇 一、总体框架二、Springcloud(一)Springcloud五大组件(二)服务注册和发现1、Eureka2、Nacos (三)负载均衡1、Ribbon负载均衡流程2、Ribbon负载均衡策略3、自定义负载均衡策略4、总结 …...
