力扣(LeetCode)240. 搜索二维矩阵 II(C++)
题目描述
枚举
枚举整个矩阵,找到等于 target 的元素,则 return true ,否则 return false。
class Solution {
public:bool searchMatrix(vector<vector<int>>& matrix, int target) {int n = matrix.size(), m = matrix[0].size();for (auto &x : matrix)for (auto &t : x)if (t == target) return true;return false;}
};
- 时间复杂度 : O(n×m)O(n\times m)O(n×m) , nnn 是数组的行数,mmm 是数组的列数,枚举所有元素,时间复杂度 O(n×m)O(n\times m)O(n×m) 。
- 空间复杂度 : O(1)O(1)O(1) , 只使用常量级空间 。
二分查找
二分优化枚举。按行枚举矩阵,由于每行元素有序,可以二分查找行内的元素。
class Solution {
public:bool searchMatrix(vector<vector<int>>& matrix, int target) {int n = matrix.size(), m = matrix[0].size();for (auto &x : matrix) {int l = 0, r = m - 1;while(l <= r) {int mid = l + (r - l >> 1);if (x[mid] < target) l = mid + 1;else r = mid - 1;}if (l < m && x[l] == target) return true;}return false;}
};
- 时间复杂度 : O(nlogm)O(nlogm)O(nlogm) , nnn 是数组的行数,mmm 是数组的列数,一次枚举一行,每行二分查找,时间复杂度 O(nlogm)O(nlogm)O(nlogm) 。
- 空间复杂度 : O(1)O(1)O(1) , 只使用常量级空间 。
枚举行列
更大胆的,同时枚举行列。这是由于每行元素有序,每列元素同样有序。
目的:保证被枚举元素与 target 的大小关系,对应唯一的移动方向
结论:从右上角枚举到左下角,根据右上角元素与 target 的大小关系,确定枚举的移动方向。
证明:右上角元素是一行的最大元素,一列的最小元素。往左下枚举,要找比他小的元素,只能同行往左;要找比他大的元素,只能同列向下。即
右上角元素 >\gt> target,往左;右上角元素 <\lt< target,往下。
朴素错法
- 为什么从左上角枚举到右下角不行?
答:左上角元素是一行的最小元素,一列的最小元素。往右下枚举,要找比他大的元素,不能确定往右还是往下。
class Solution {
public:bool searchMatrix(vector<vector<int>>& matrix, int target) {int n = matrix.size(), m = matrix[0].size();int i = 0, j = m - 1;while(i < n && j >= 0) {if (matrix[i][j] > target) j --;else if (matrix[i][j] < target) i ++;else return true;}return false;}
};
- 时间复杂度 : O(n+m)O(n+m)O(n+m) , nnn 是数组的行数,mmm 是数组的列数,一次枚举,移动一列或者一行,时间复杂度 O(n+m)O(n+m)O(n+m) 。
- 空间复杂度 : O(1)O(1)O(1) , 只使用常量级空间 。
AC
按行列枚举,执行结果。

致语
- 理解思路很重要
- 读者有问题请留言,清墨看到就会回复的。
相关文章:

力扣(LeetCode)240. 搜索二维矩阵 II(C++)
题目描述 枚举 枚举整个矩阵,找到等于 target 的元素,则 return true ,否则 return false。 class Solution { public:bool searchMatrix(vector<vector<int>>& matrix, int target) {int n matrix.size(), m matrix[0]…...

golang defer
文章目录延迟函数的参数在defer语句出现时就已经确定下来了延迟函数没有入参时,延迟函数体内的变量会受到影响延迟函数 *可以* 修改主函数的 *具名* 返回值延迟函数 *无法* 修改主函数的 *匿名* 返回值defer会把声明的 延迟函数以及 函数的入参放到栈上,…...
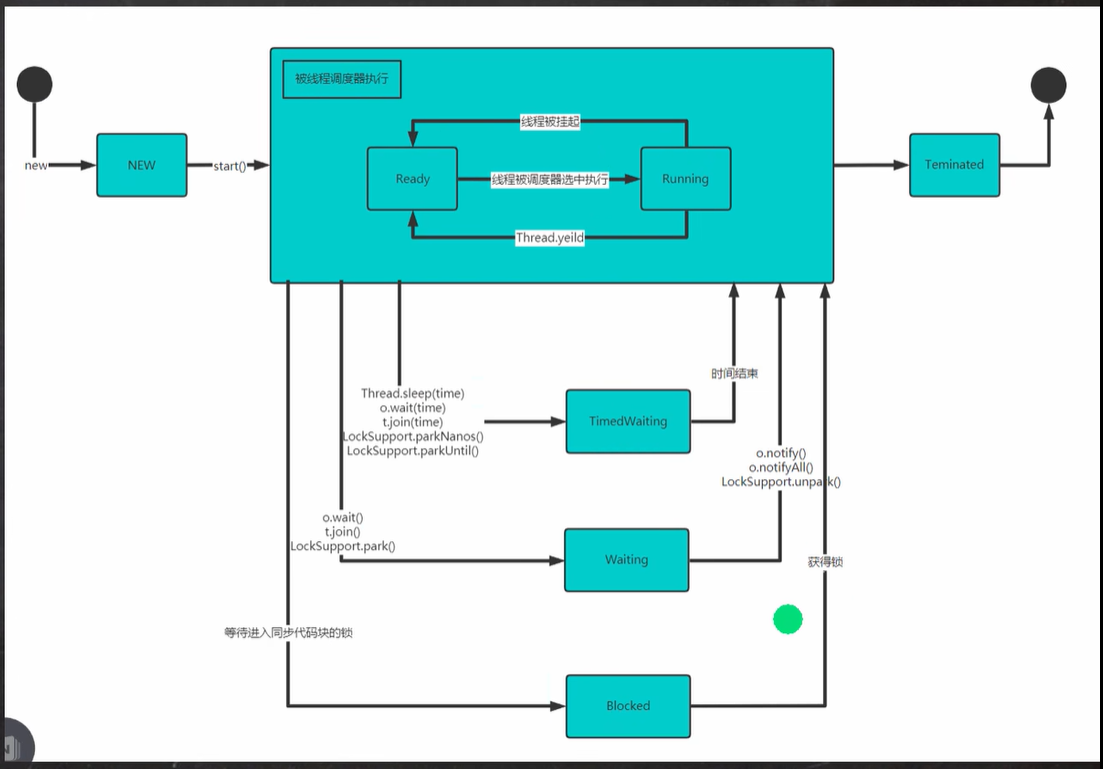
【Java】线程的死锁和释放锁
线程死锁是线程同步的时候可能出现的一种问题 文章目录1. 线程的死锁1.1 基本介绍1.2 应用案例2. 释放锁2.1 下面的操作会释放锁2.2 下面的操作不会释放锁1. 线程的死锁 1.1 基本介绍 多个线程都占用了对方的锁资源,但不肯相让,导致了死锁,…...
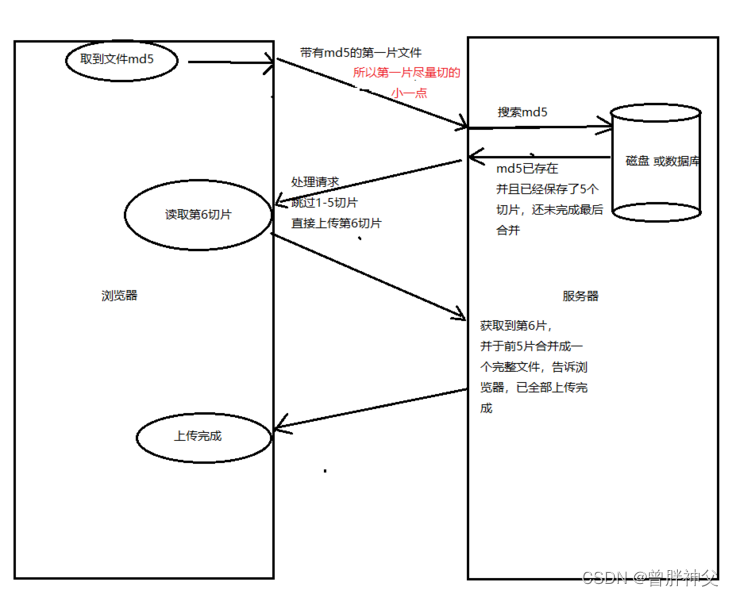
如何使用断点续传上传大文件
概念 大文件上传的需求介绍 不管怎样简单的需求,在量级达到一定层次时,都会变得异常复杂。 文件上传简单,文件变大就复杂 上传大文件时,以下几个变量会影响我们的用户体验 服务器处理数据的能力请求超时网络波动 上传时间会变长…...
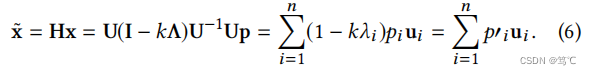
【图神经网络】图拉普拉斯滤波器如何实现全通、低通、高通滤波
【图神经网络】图拉普拉斯滤波器如何实现全通、低通、高通滤波 文章目录【图神经网络】图拉普拉斯滤波器如何实现全通、低通、高通滤波1. 前言2. 符号说明3. 三种滤波3.1 全通滤波3.2 低通滤波3.2.1 平滑信号分析3.2.2 广义拉普拉斯平滑滤波器3.3 高通滤波4. 总结1. 前言 GCN&…...

python操作mysql数据库详解
使用Python操作MySQL数据库 MySQL是一种关系型数据库管理系统,它可以用来存储和管理大量的数据。之前介绍了大部分主流数据库,今天将介绍如何使用Python来操作MySQL数据库。 安装MySQL 首先,我们需要安装MySQL服务器,可以从MyS…...
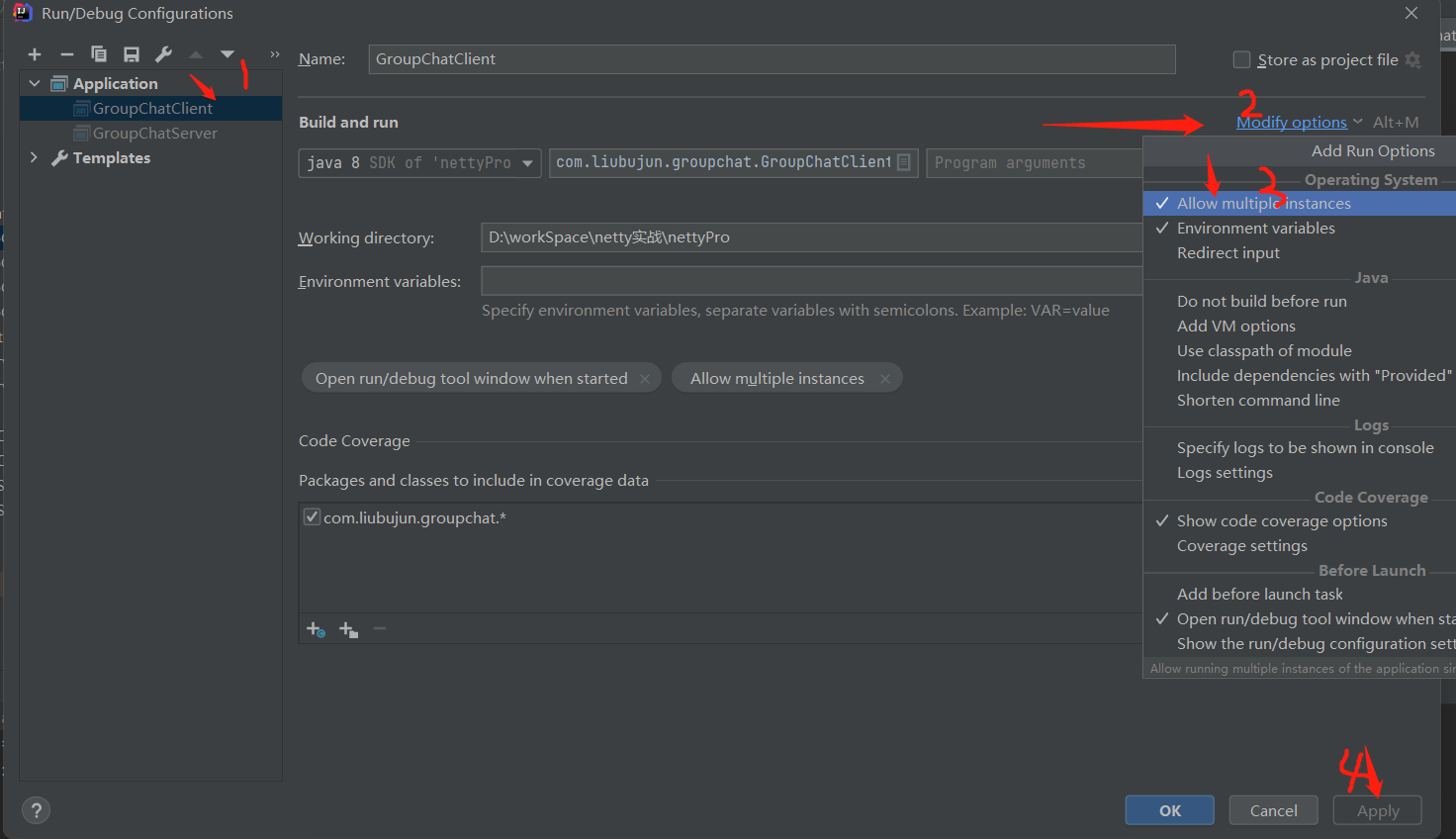
netty群聊系统
1设计思路:启动一个服务端,多个客户端第一个客户端启动时,会告诉服务器上线了第二个客户端启动时,告诉服务器上线,并且通知第一个启动的客户端第三个客户端启动时,告诉服务器上线,并且通知第一个…...
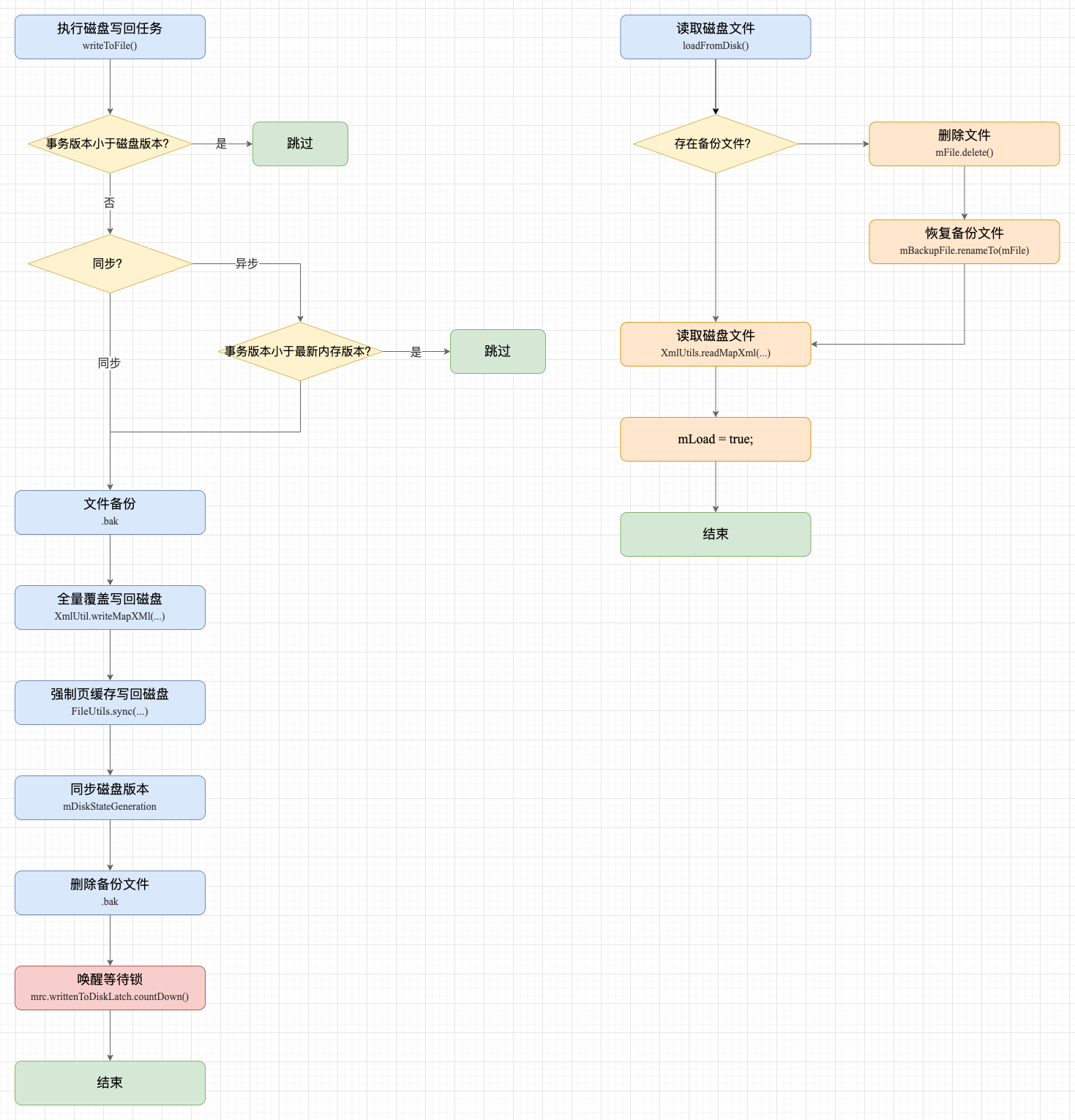
Android 初代 K-V 存储框架 SharedPreferences,旧时代的余晖?
本文已收录到 AndroidFamily,技术和职场问题,请关注公众号 [彭旭锐] 提问。 前言 大家好,我是小彭。 SharedPreferences 是 Android 平台上轻量级的 K-V 存储框架,亦是初代 K-V 存储框架,至今被很多应用沿用。 有的…...
在windows中使用tomcat搭建Jenkins
1、 准备环境:JDK JDK官网下载:https://download.oracle.com/java/19/latest/jdk-19_windows-x64_bin.msi 2、 tomcat包 tocat官网下载:https://tomcat.apache.org/download-90.cgi 3、 Jenkins.war包 Jenkins官网下载:https://mi…...

Linux系统
linux系统 世界上最重要的服务器端操作系统。 创建新目录 mkdir app mkdir -m 目录权限 目录名 创建有权限的目录名。 创建一个空白文件 touch app.txt创建一个文件。 cat创建一个文件。 vi/vim创建一个文件。 nano创建一个文件。 truncate创建一个文件。 pwd查看当前目录。 rm…...
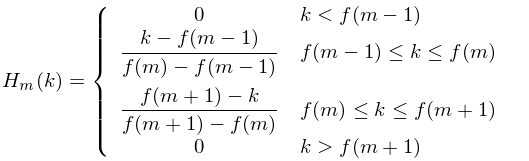
Mel Frequency Cepstral Coefficients (MFCCs)
wiki里说 在声音处理中,梅尔频率倒谱( MFC ) 是声音的短期功率谱的表示,基于非线性梅尔频率标度上的对数功率谱的线性余弦变换。 倒谱和MFC 之间的区别在于,在 MFC 中,频带在梅尔尺度上等距分布,这比正常频谱中使用的线…...
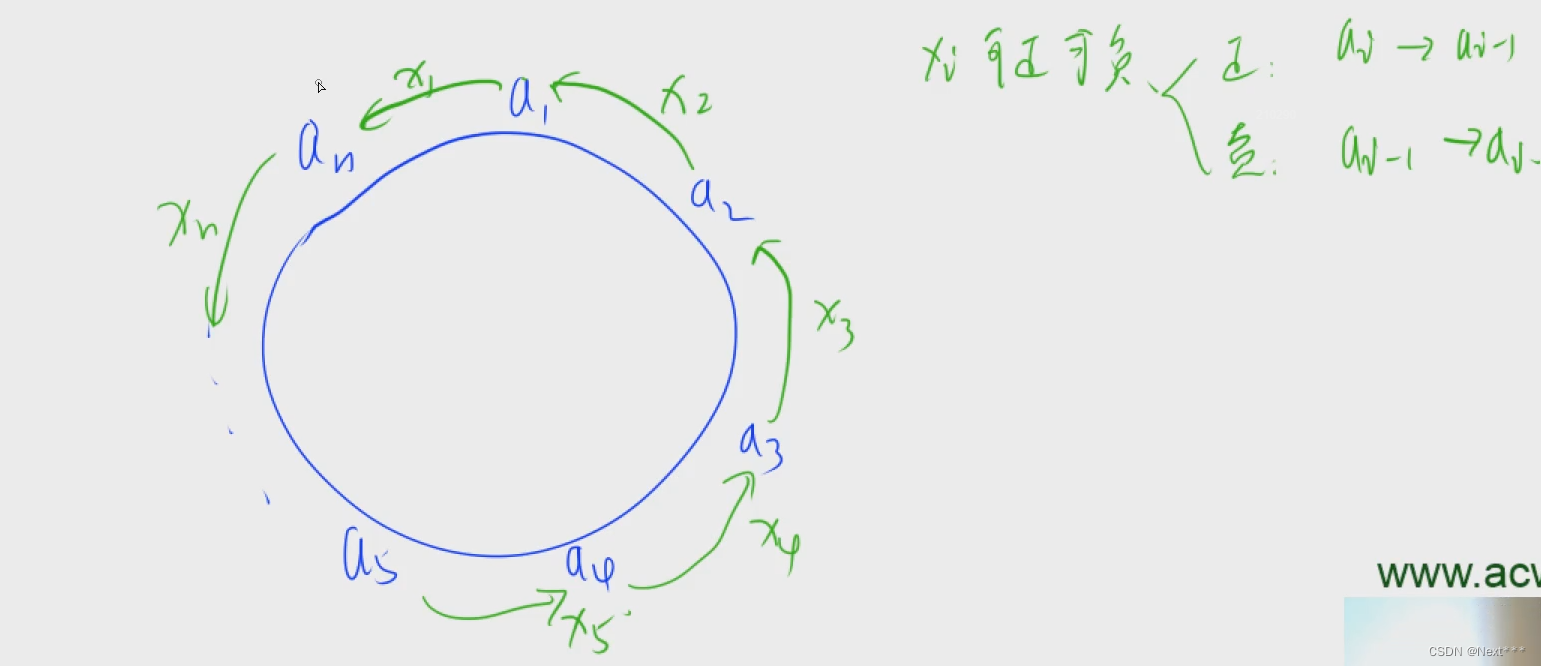
第七讲---贪心(上课)
1.股票买卖 一、贪心 考虑一种方案,在每次上升的前一天购入股票,并在上升后的当天卖出的方案 if (w[i] > w[i - 1])res w[i] - w[i - 1];接下来证明该贪心思路得出的方案即是最优解。 (1)证明贪心解 ≥ 最优解: …...

计算机如何思考与图灵完备
图灵完备是针对一套数据操作规则而言的概念,数据操作规则可以是一门编程语言,也可以是计算机实现里面的指令集,比如C/C++是图图灵完备的,通用CPU也是图灵完备的,但是GPU却不一定是图灵完备的。说白了图灵完备定义了一套规则,当这套规则可以实现图灵迹模型里的全部功能时,…...

惠普LaserJet M1005 MFP报错b2
故障现象: 惠普LaserJet M1005 MFP开机后直接报b2错误; 检测维修: 故障大意是:机器的硬件可能出现点突变,此问题建议联系当地维修中心进行处理。...
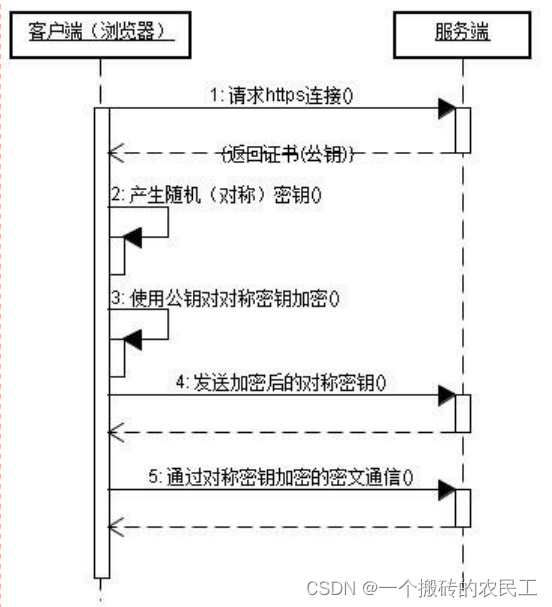
网络协议(TCP/IP)
目录一、网络分层模型二、OSI模型三、网络传输原理四、TCP/IP1、TCP/IP 原理2、TCP 三次握手/四次挥手3、Http协议和TCP/IP的区别五、HTTP原理六、HTTPS原理七、CDN原理一、网络分层模型 互联网的本质就是一系列的网络协议,最早由ISO国际组织定义为7层网络参考模型…...

2023河南省第二届职业技能大赛郑州市选拔赛“网络安全” 项目比赛样题任务书
2023河南省第二届职业技能大赛郑州市选拔赛“网络安全” 项目比赛样题任务书2023河南省第二届职业技能大赛郑州市选拔赛“网络安全” 项目比赛样题任务书A模块基础设施设置/安全加固(200分)A-1:登录安全加固(Windows, Linux&#…...

6、流程控制
目录一、if二、switch三、for四、break与continue五、goto与Label一、if if使用:逻辑表达式成立,就会执行{}里的内容;逻辑表达式不需要加() if 5 > 9 {fmt.Println("5>9") }if句子中允许包含1个(仅1个)分号:在分…...

Linux中最基本常见命令总结
❤❤💛💛💚💚💙💙💜💜您的认可是对我最大的帮助💜💜💙💙💚💚💛💛❤❤ 🤎&…...

Python学习-----模块2.0(常用模块之时间模块-->time)
目录 前言: time简介 导入模块 1.时间戳 2.时间元组 (1)把时间戳转换为元组形式 (2)元组转换为时间戳输出 (3)把元组转换为格式化时间 (4)把时间戳转换为格式化时间…...
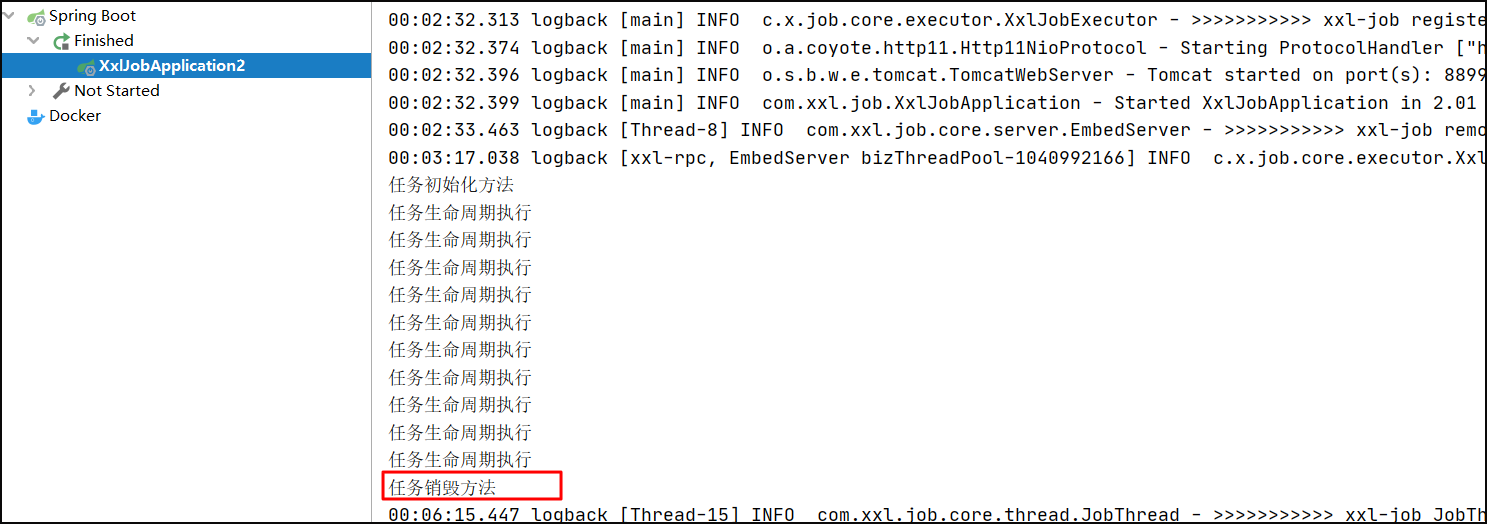
XXL-JOB分布式任务调度框架(二)-策略详解
文章目录1.引言2.任务详解2.1.执行器2.2.基础配置3.路由策略(第一个)-案例4.路由策略(最后一个)-案例5.轮询策略-案例6.随机选取7.轮询选取8.一致性hash9.最不经常使用 (LFU)10.最近最久未使用(LRU)11.故障转移12.忙碌转移13.分片广播任务14.父子任务15.…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...
