第七讲---贪心(上课)

1.股票买卖
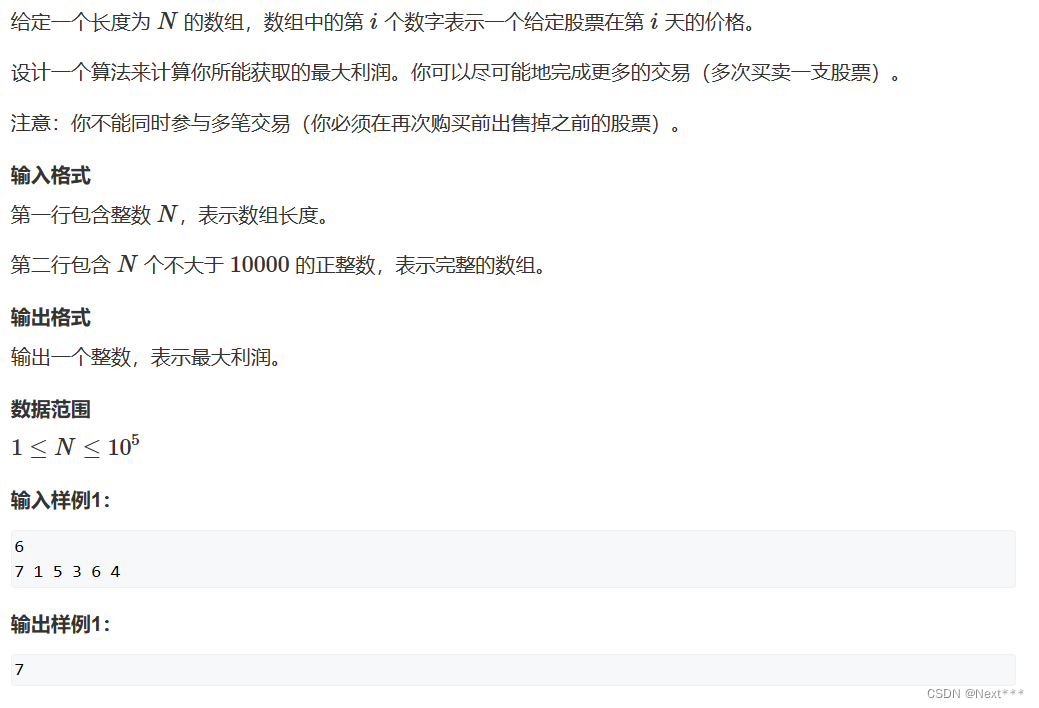
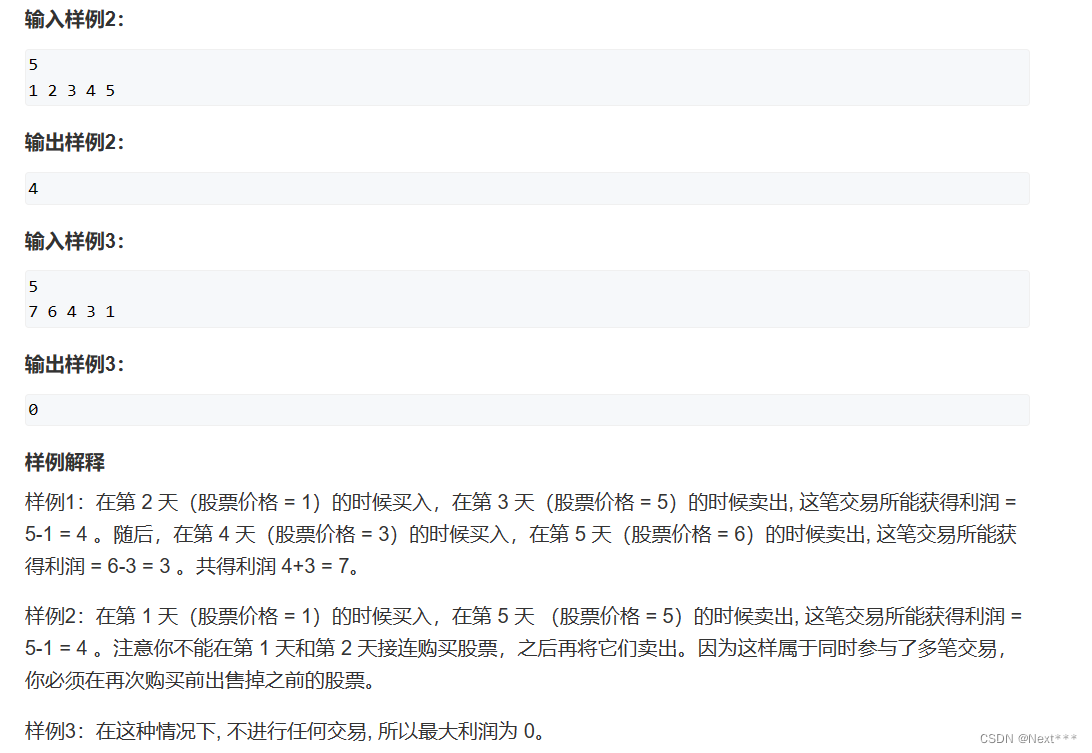
一、贪心

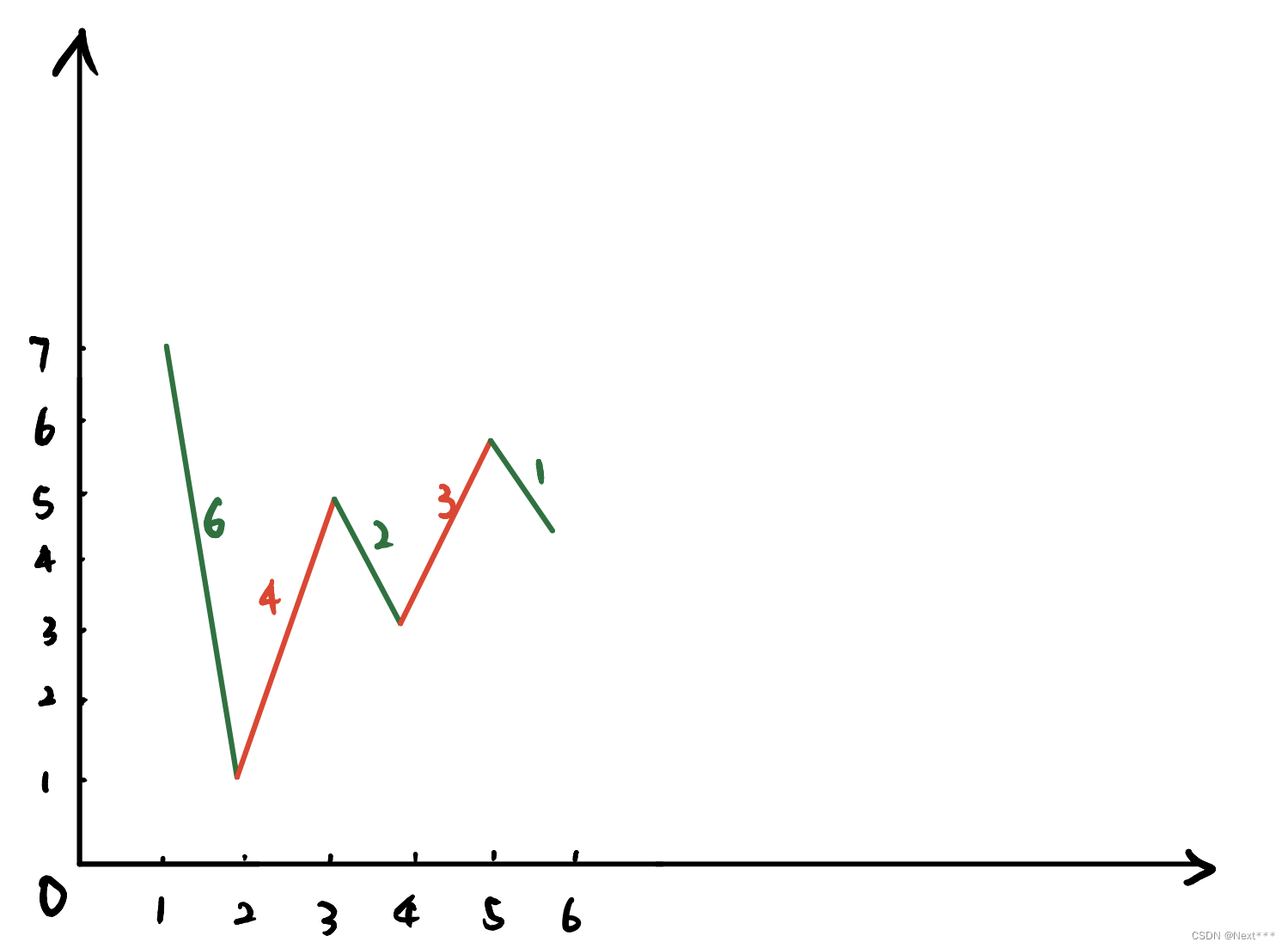
考虑一种方案,在每次上升的前一天购入股票,并在上升后的当天卖出的方案
if (w[i] > w[i - 1])res += w[i] - w[i - 1];
接下来证明该贪心思路得出的方案即是最优解。
(1)证明贪心解 ≥ 最优解:
由于贪心解都是取区间长度为 1 的解,因此假设存在于最优解中的某个区间 [i,j] 的长度 >1
那么会出现一下三种情况:
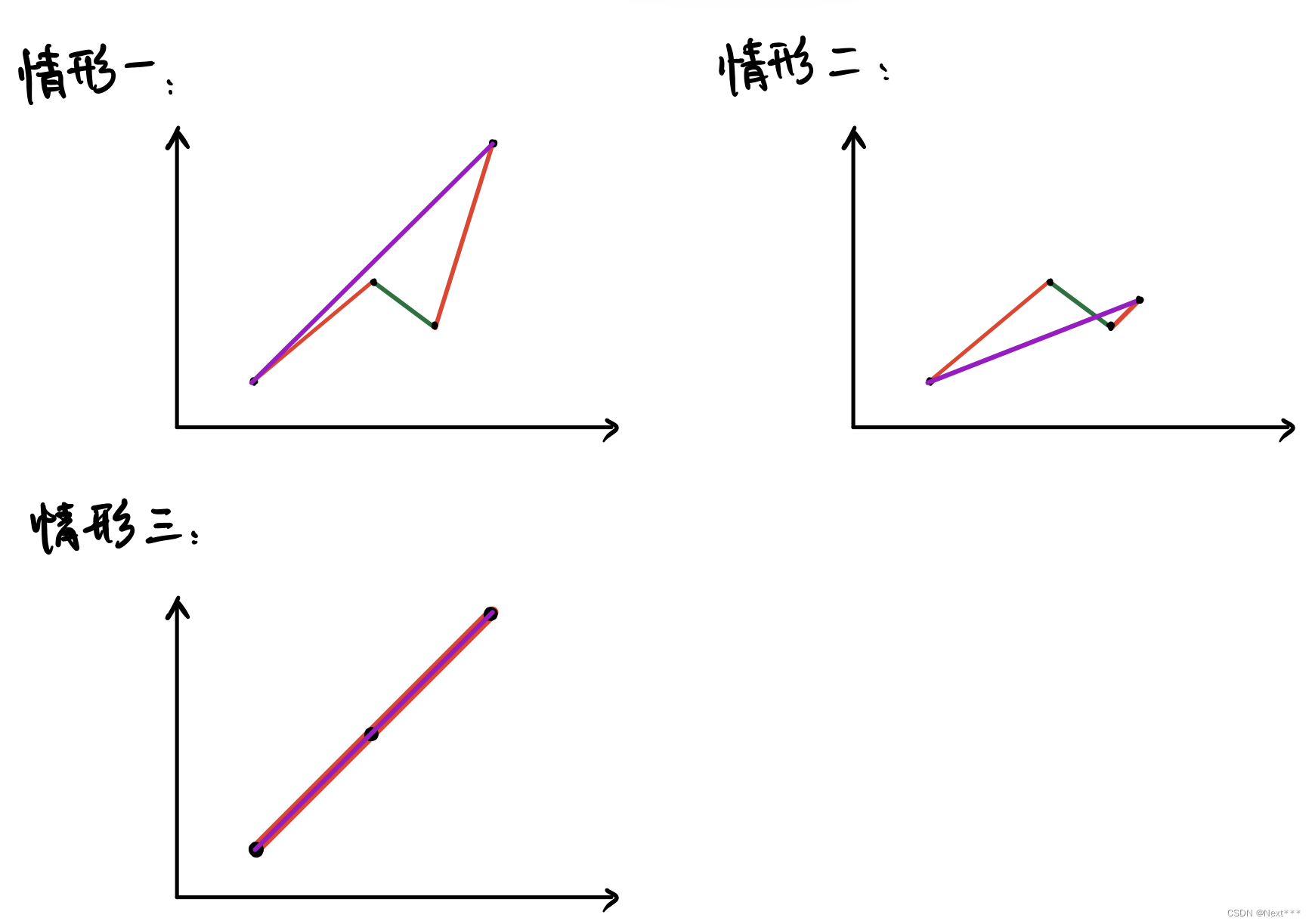
对应三种情形:最优解选取的区间最终点位于上方、下方、相等。
对于情形一:显然 最优解 < 贪心解
对于情形二:显然 最优解 <贪心解
对于情形三:毫无疑问,这就是存在于贪心解中的情形,因此 贪心解 = 最优解
得证
(2)证明贪心解 ≤最优解:
这部分无需证明,因为贪心解即是合法解,所以他的方案必定大于等于最优解
#include <iostream>
using namespace std;
const int N = 1e5 + 10;
int n;
int w[N];int main() {scanf("%d", &n);for (int i = 1; i <= n; ++i) scanf("%d", &w[i]);int res = 0;for (int i = 2; i <= n + 1; ++i) {if (w[i] - w[i - 1] > 0) res += w[i] - w[i - 1];}printf("%d\n", res);return 0;
}二、闫氏DP分析法
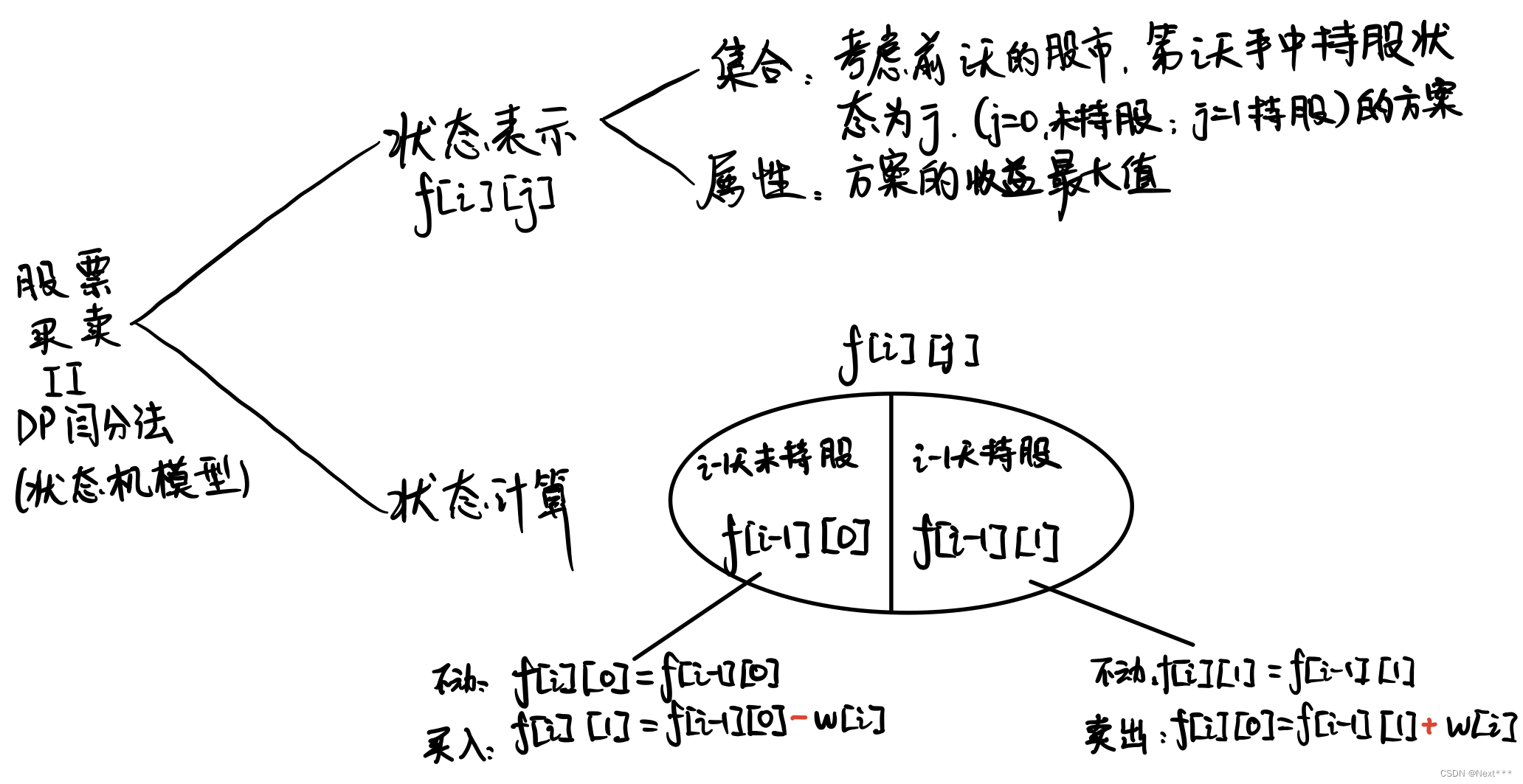
具体的状态机模型分析如下图:
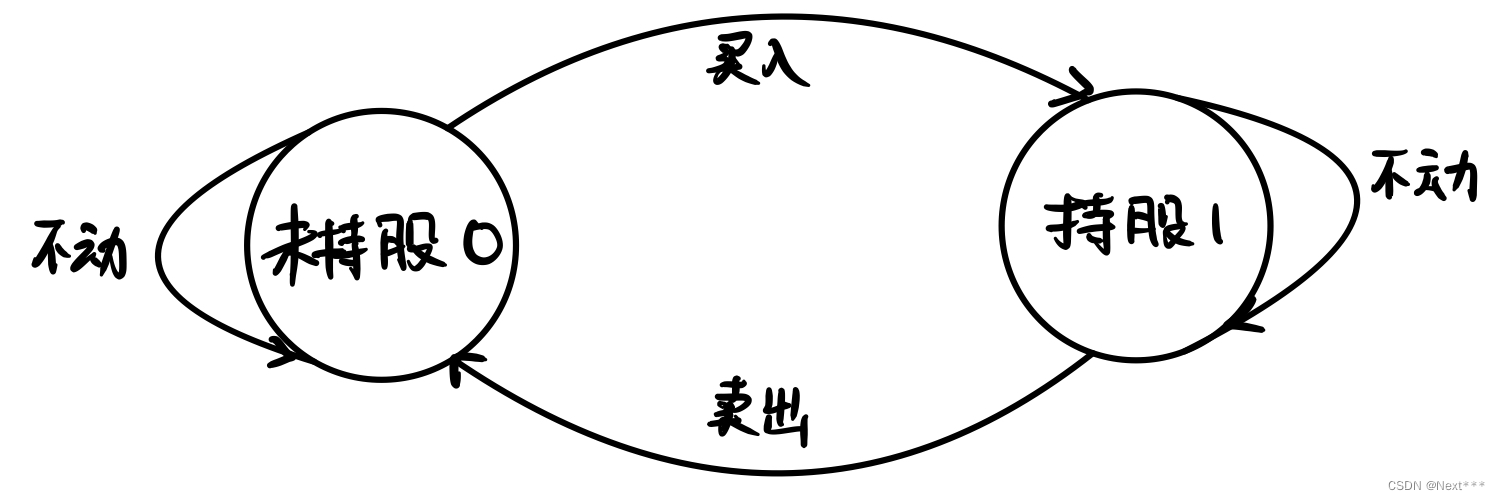
一共只2有种状态:
1. 当前处于未持股状态0:
对应可以进行的转换:
0->0 (不买入,继续观望,那么就什么都不发生)
0->1 (买入股票,那么收益就要减去当前市场的股票价格)
2. 当前处于持股状态1:
对应可以进行的转换:
1->1 (不卖出,继续观望,那么就什么都不发生)
1->0 (卖出股票,那么收益就要加上当前市场的股票价格)
#include <iostream>
using namespace std;
const int N = 1e5 + 10, INF = 0x3f3f3f3f;
int n;
int w[N];
int f[N][2];int main() {scanf("%d", &n);for (int i = 1; i <= n; ++i) scanf("%d", &w[i]);f[0][1] = -INF;for (int i = 1; i <= n; ++i) {f[i][0] = max(f[i - 1][0], f[i - 1][1] + w[i]);f[i][1] = max(f[i - 1][1], f[i - 1][0] - w[i]);}printf("%d\n", f[n][0]);return 0;
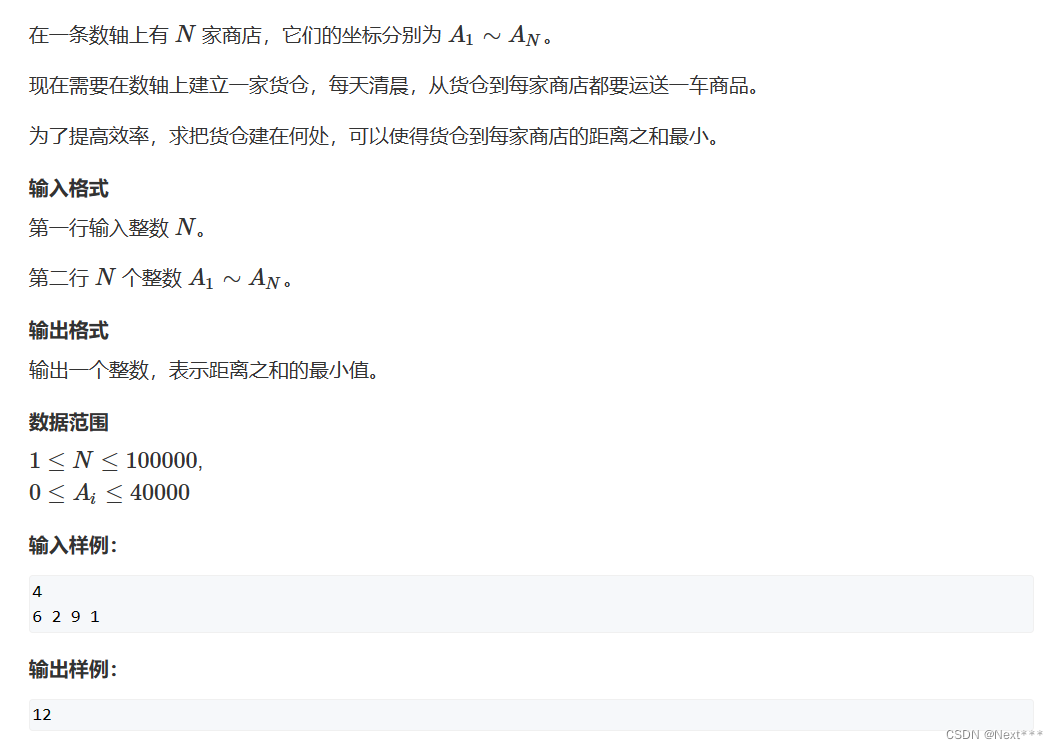
}2.货舱选址
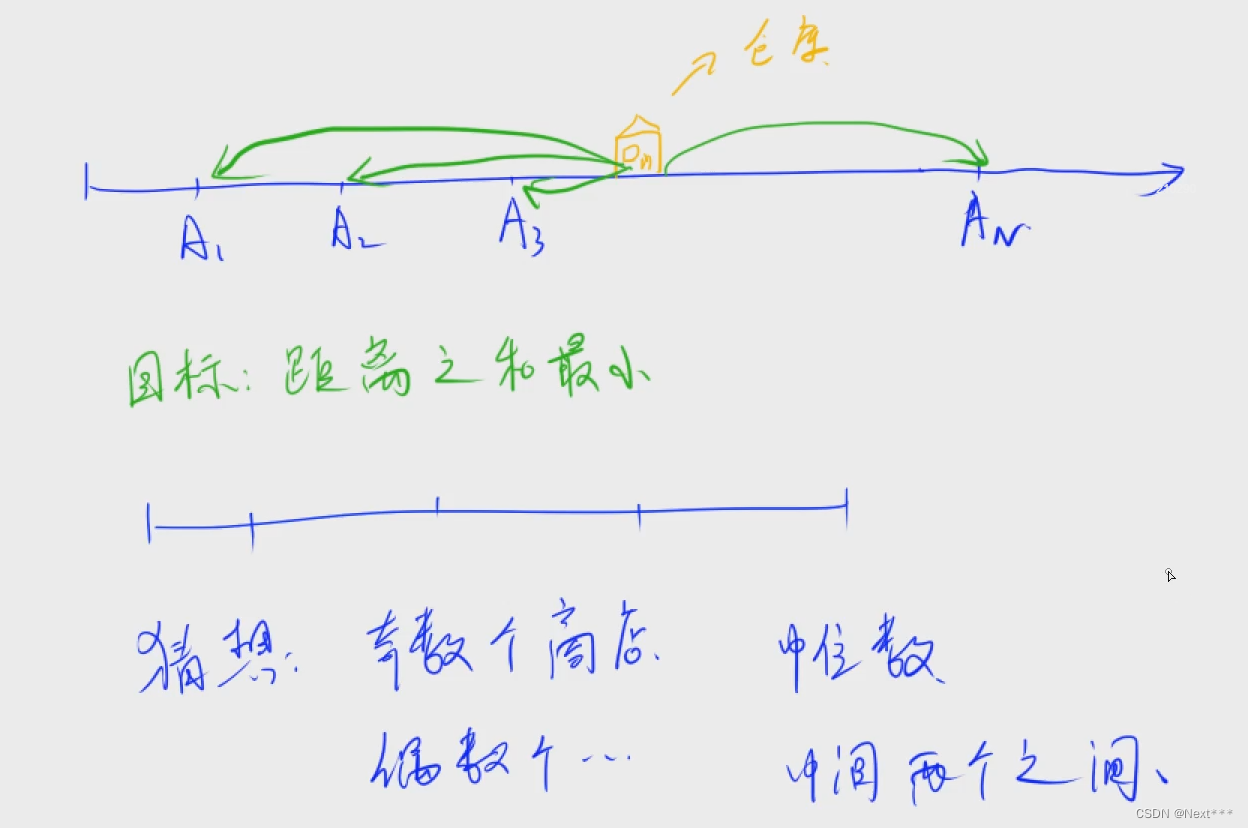

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 100010;
int n;
int a[N];
int main () {scanf ("%d",&n);for (int i = 1;i <= n;i++) scanf ("%d",&a[i]);sort (a + 1,a + 1 + n);int ans = 0;for (int i = 1,j = n;i <= j;i++,j--) ans += a[j] - a[i];printf ("%d\n",ans);return 0;
}
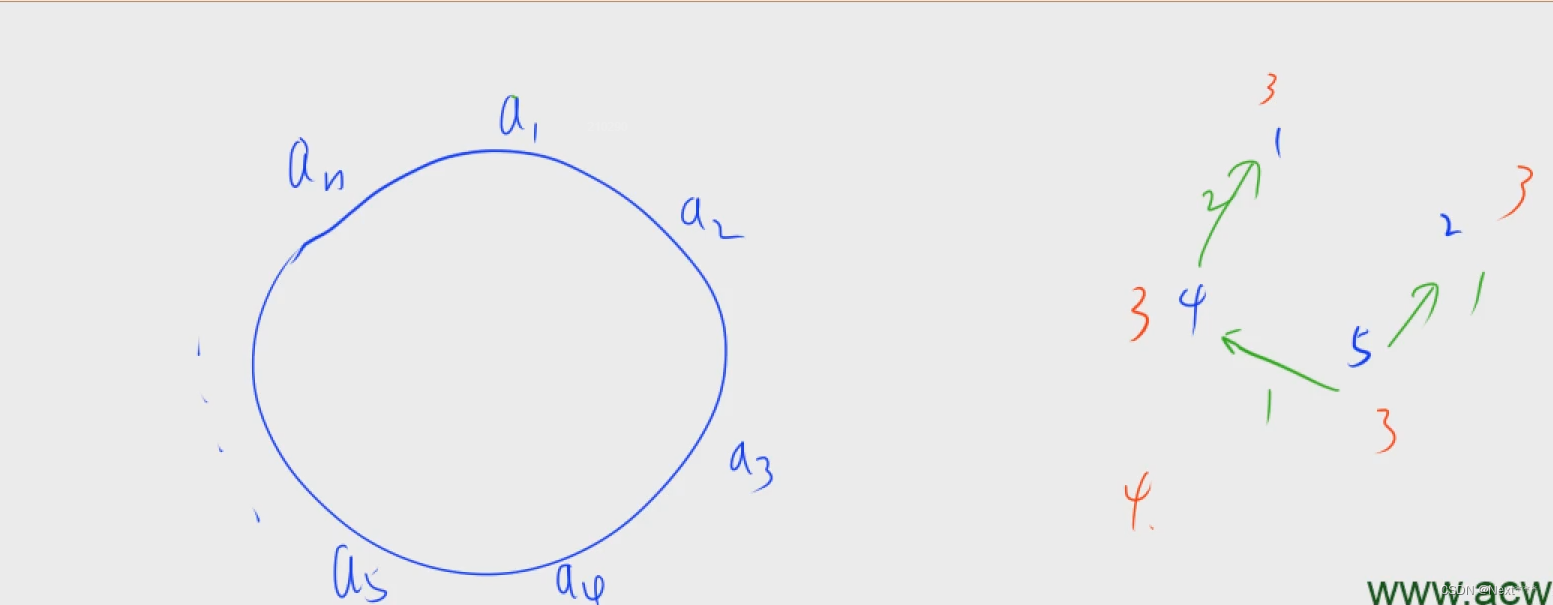
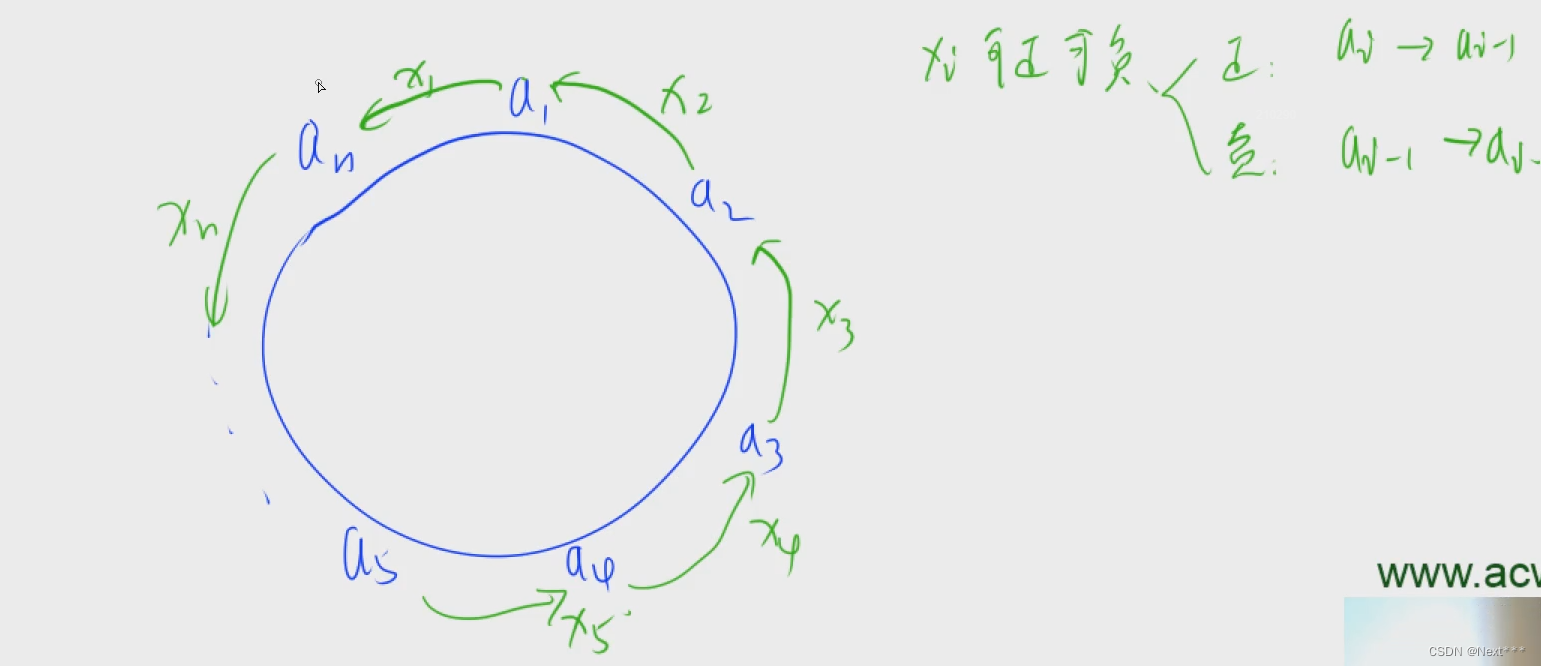
3.糖果传递
相关文章:

第七讲---贪心(上课)
1.股票买卖 一、贪心 考虑一种方案,在每次上升的前一天购入股票,并在上升后的当天卖出的方案 if (w[i] > w[i - 1])res w[i] - w[i - 1];接下来证明该贪心思路得出的方案即是最优解。 (1)证明贪心解 ≥ 最优解: …...

计算机如何思考与图灵完备
图灵完备是针对一套数据操作规则而言的概念,数据操作规则可以是一门编程语言,也可以是计算机实现里面的指令集,比如C/C++是图图灵完备的,通用CPU也是图灵完备的,但是GPU却不一定是图灵完备的。说白了图灵完备定义了一套规则,当这套规则可以实现图灵迹模型里的全部功能时,…...

惠普LaserJet M1005 MFP报错b2
故障现象: 惠普LaserJet M1005 MFP开机后直接报b2错误; 检测维修: 故障大意是:机器的硬件可能出现点突变,此问题建议联系当地维修中心进行处理。...
网络协议(TCP/IP)
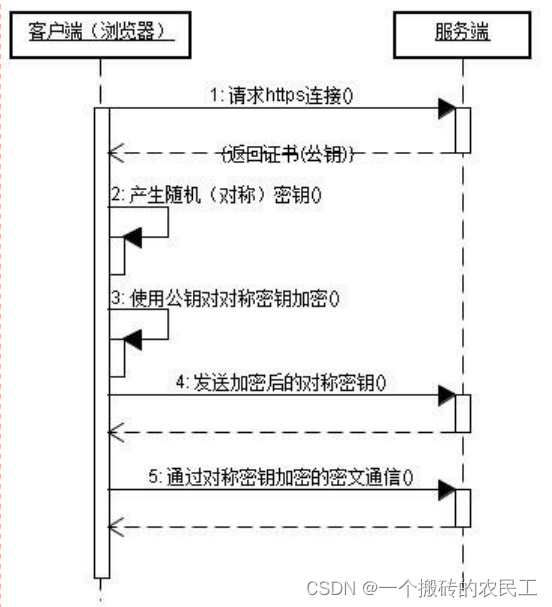
目录一、网络分层模型二、OSI模型三、网络传输原理四、TCP/IP1、TCP/IP 原理2、TCP 三次握手/四次挥手3、Http协议和TCP/IP的区别五、HTTP原理六、HTTPS原理七、CDN原理一、网络分层模型 互联网的本质就是一系列的网络协议,最早由ISO国际组织定义为7层网络参考模型…...

2023河南省第二届职业技能大赛郑州市选拔赛“网络安全” 项目比赛样题任务书
2023河南省第二届职业技能大赛郑州市选拔赛“网络安全” 项目比赛样题任务书2023河南省第二届职业技能大赛郑州市选拔赛“网络安全” 项目比赛样题任务书A模块基础设施设置/安全加固(200分)A-1:登录安全加固(Windows, Linux&#…...

6、流程控制
目录一、if二、switch三、for四、break与continue五、goto与Label一、if if使用:逻辑表达式成立,就会执行{}里的内容;逻辑表达式不需要加() if 5 > 9 {fmt.Println("5>9") }if句子中允许包含1个(仅1个)分号:在分…...

Linux中最基本常见命令总结
❤❤💛💛💚💚💙💙💜💜您的认可是对我最大的帮助💜💜💙💙💚💚💛💛❤❤ 🤎&…...

Python学习-----模块2.0(常用模块之时间模块-->time)
目录 前言: time简介 导入模块 1.时间戳 2.时间元组 (1)把时间戳转换为元组形式 (2)元组转换为时间戳输出 (3)把元组转换为格式化时间 (4)把时间戳转换为格式化时间…...
XXL-JOB分布式任务调度框架(二)-策略详解
文章目录1.引言2.任务详解2.1.执行器2.2.基础配置3.路由策略(第一个)-案例4.路由策略(最后一个)-案例5.轮询策略-案例6.随机选取7.轮询选取8.一致性hash9.最不经常使用 (LFU)10.最近最久未使用(LRU)11.故障转移12.忙碌转移13.分片广播任务14.父子任务15.…...

JAVA练习54-最小栈
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 目录 前言 一、题目-最小栈 1.题目描述 2.思路与代码 2.1 思路 2.2 代码 总结 前言 提示:这里可以添加本文要记录的大概内容: 2月18日练习内容…...

Redis-哨兵模式以及集群
在开始这部分内容之前需要先说一下复制功能,因为这是Redis实现主从数据同步的实现方式。复制功能如果存在两台服务器的话,我们可以使用redis的复制功能,让一台服务器去同步另一台服务器的数据。现在我启动了两台redis服务器,一个端…...

过滤器和监听器
1、过滤器Filter 作用是防止SQL注入、参数过滤、防止页面攻击、空参数矫正、Token校验、Session验证、点击率统计等等; 使用Filter的步骤 新建类,实现Filter抽象类;重写init、doFilter、destroy方法;在SpringBoot入口中添加注解…...

Acwing 第 91 场周赛
Powered by:NEFU AB-IN B站直播录像! Link 文章目录Acwing 第 91 场周赛A AcWing 4861. 构造数列题意思路代码B AcWing 4862. 浇花题意思路代码C AcWing 4863. 构造新矩阵题意思路代码Acwing 第 91 场周赛 A AcWing 4861. 构造数列 题意 略 思路 将每个数的每一位…...
JavaEE|套接字编程之UDP数据报
文章目录一、DatagramSocket API构造方法常用方法二、DatagramPacket API构造方法常用方法E1:回显服务器的实现E2:带有业务逻辑的请求发送一、DatagramSocket API 在操作系统中,把socket对象当成了一个文件处理。等价于是文件描述符表上的一项。 普通的文件…...
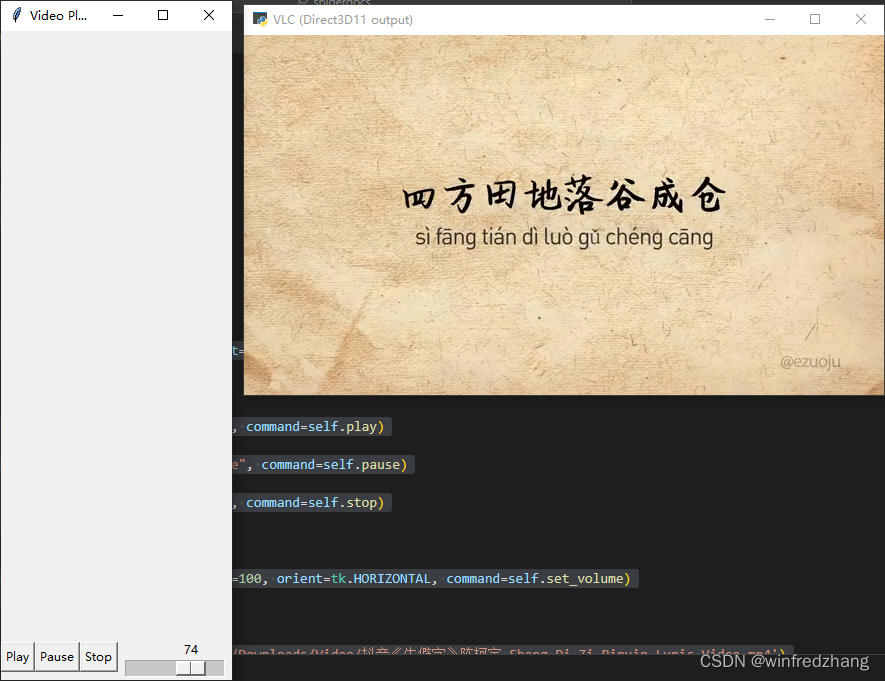
如何使用Python创建一个自定义视频播放器
目录 1、安装vlc的64位版本。 2、安装python的vlc模块。 3、编写如下代码,包含了播放,暂停,停止、音量控制功能。 4、来看一看运行结果。 5、如果遇到播放不了的问题,解决方式如下: 这个例子使用VLC作为视频播放器…...
和索引收缩(shrink ))
Elasticsearch进行优化-使用索引拆分(Split)和索引收缩(shrink )
一、索引拆分和收缩的场景 在Elasticsearch集群部署的初期我们可能评估不到位,导致分配的主分片数量太少,单分片的数据量太大,导致搜索时性能下降,这时我们可以使用Elasticsearch提供的Split功能对当前的分片进行拆分,…...
)
数论 —— 高斯记号(Gauss mark)
定义 数学上,高斯记号(Gauss mark)是指对取整符号和取小符号的统称,用于数论等领域。 设 x∈Rx \in \textbf{R}x∈R,用 [x][x][x] 表示不超过 xxx 的最大整数。也可记作 [x][x][x]。设 x∈Rx \in \textbf{R}x∈R&…...

【随笔】程序员眼中的 CPU,“没有灵魂的躯体”
引言 先引用一段比较有意思的论述: 现实中每个人是由两部分构成,灵魂和躯体,灵魂依附于躯体游走于世间,现实中我们面对的每个人其实面对的是其灵魂而非肉体,肉体不过是表象而已。 灵魂本性乃一恶物,寄生于…...

算法的时间复杂度
算法在编写成可执行程序后,运行时需要消耗时间资源和空间(内存)资源,因此衡量一个算法的好坏,一般是从时间和空间两个维度来衡量的。 时间复杂度主要衡量一个算法运行的快慢,而空间复杂度主要衡量一个算法运…...
 | 机试题算法思路 【2023】)
华为OD机试 - 叠放书籍(Python) | 机试题算法思路 【2023】
最近更新的博客 华为OD机试 - 寻找路径 | 备考思路,刷题要点,答疑 【新解法】 华为OD机试 - 五键键盘 | 备考思路,刷题要点,答疑 【新解法】 华为OD机试 - IPv4 地址转换成整数 | 备考思路,刷题要点,答疑 【新解法】 华为OD机试 - 对称美学 | 备考思路,刷题要点,答疑 …...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...

Qt 事件处理中 return 的深入解析
Qt 事件处理中 return 的深入解析 在 Qt 事件处理中,return 语句的使用是另一个关键概念,它与 event->accept()/event->ignore() 密切相关但作用不同。让我们详细分析一下它们之间的关系和工作原理。 核心区别:不同层级的事件处理 方…...

基于江科大stm32屏幕驱动,实现OLED多级菜单(动画效果),结构体链表实现(独创源码)
引言 在嵌入式系统中,用户界面的设计往往直接影响到用户体验。本文将以STM32微控制器和OLED显示屏为例,介绍如何实现一个多级菜单系统。该系统支持用户通过按键导航菜单,执行相应操作,并提供平滑的滚动动画效果。 本文设计了一个…...

【把数组变成一棵树】有序数组秒变平衡BST,原来可以这么优雅!
【把数组变成一棵树】有序数组秒变平衡BST,原来可以这么优雅! 🌱 前言:一棵树的浪漫,从数组开始说起 程序员的世界里,数组是最常见的基本结构之一,几乎每种语言、每种算法都少不了它。可你有没有想过,一组看似“线性排列”的有序数组,竟然可以**“长”成一棵平衡的二…...
