DP(区间DP)
石子合并
设有 N 堆石子排成一排,其编号为 1,2,3,…,N。
每堆石子有一定的质量,可以用一个整数来描述,现在要将这 N 堆石子合并成为一堆。
每次只能合并相邻的两堆,合并的代价为这两堆石子的质量之和,合并后与这两堆石子相邻的石子将和新堆相邻,合并时由于选择的顺序不同,合并的总代价也不相同。
例如有 4 堆石子分别为 1 3 5 2, 我们可以先合并 1、2堆,代价为 4,得到 4 5 2, 又合并 1、2堆,代价为 9,得到 9 2 ,再合并得到 11,总代价为 4+9+11=24
如果第二步是先合并 2、3堆,则代价为 7,得到 4 7,最后一次合并代价为 11,总代价为 4+7+11=22。
问题是:找出一种合理的方法,使总的代价最小,输出最小代价。
输入格式
第一行一个数 N 表示石子的堆数 N。
第二行 N 个数,表示每堆石子的质量(均不超过 1000)。
输出格式
输出一个整数,表示最小代价。
数据范围
1≤N≤300
输入样例:
4
1 3 5 2
输出样例:
22 
每个状态只会依赖比它长度更短的其他状态,所以先枚举长度可以保证在计算每个状态之前,先计算出它所依赖的状态。
如果先枚举 i
可以知道
起点小于 i 的所有情况;
起点为i,长度小于 len的所有情况
不能知道
起点大于i 的所有情况
起点为i,长度大于 len的情况
如果先枚举 len
可以知道
长度小于 len的所有情况
长度为 len,起点小于 i 的所有情况
不能知道
长度大于 len的所有情况
长度为 len,起点大于 i 的情况
需求:
f[i][k] :起点为 i,长度为 k - i + 1 < len 两种都可以
f[k+1][j] :起点为 k + 1 > i,长度为 j - k < len 不能先枚举 i
#include<iostream>
#include<cstring>
using namespace std;
const int N=330;
int f[N][N];//f[i][j]表示第i堆石子到第j堆石子(一段区间)合并成一堆需要的最小代价
int w[N],s[N];
int main()
{int n;cin>>n;for(int i=1;i<=n;i++)cin>>w[i];memset(f,0x3f,sizeof f);//求最小值 故需要初始化最大for(int i=0;i<=n;i++) f[i][i]=0;//i到i只有自己 不需要花费 for(int i=1;i<=n;i++) s[i]=s[i-1]+w[i];//前缀和for(int len=2;len<=n;len++){for(int i=1;i+len-1<=n;i++)//枚举长度{int l=i,r=i+len-1;//区间的左端点 右端点for(int k=1;k<r;k++){//计算i到j 合并成一堆 最后肯定是 在l--r区间中一个分界线合成一堆 //先不求最后那一和 合成左堆最小代价 f[l][k] 合成右堆的最小代价 f[k+1][r]//最后一步将左右两堆合起来 左堆的最小代价+右堆的最小代价+(合成最后一步就是l-r的代价)f[l][r]=min(f[l][r],f[l][k]+f[k+1][r]+s[r]-s[l-1]);}}}cout<<f[1][n]<<endl;//输出从第一堆石子到第n堆石子合并为一堆石子的最小代价return 0;
}合并果子(贪心 Huffman树)
在一个果园里,达达已经将所有的果子打了下来,而且按果子的不同种类分成了不同的堆。
达达决定把所有的果子合成一堆。
每一次合并,达达可以把两堆果子(任意两堆,不受限制)合并到一起,消耗的体力等于两堆果子的重量之和。
可以看出,所有的果子经过 n−1 次合并之后,就只剩下一堆了。
达达在合并果子时总共消耗的体力等于每次合并所耗体力之和。
因为还要花大力气把这些果子搬回家,所以达达在合并果子时要尽可能地节省体力。
假定每个果子重量都为 1,并且已知果子的种类数和每种果子的数目,你的任务是设计出合并的次序方案,使达达耗费的体力最少,并输出这个最小的体力耗费值。
例如有 3 种果子,数目依次为 1,2,9。
可以先将 1、2堆合并,新堆数目为 3,耗费体力为 3。
接着,将新堆与原先的第三堆合并,又得到新的堆,数目为 12,耗费体力为 12。
所以达达总共耗费体力=3+12=15。
可以证明 15 为最小的体力耗费值。
输入格式
输入包括两行,第一行是一个整数 n,表示果子的种类数。
第二行包含 n 个整数,用空格分隔,第 i 个整数 ai 是第 i 种果子的数目。
输出格式
输出包括一行,这一行只包含一个整数,也就是最小的体力耗费值。
输入数据保证这个值小于 231。
数据范围
1≤n≤10000
1≤ai≤20000
输入样例:
3
1 2 9
输出样例:
15经典的Huffman树 每次合并重量最小的两堆果子即可

#include<iostream>
#include<algorithm>
#include<queue>
using namespace std;
int main()
{priority_queue<int,vector<int>,greater<int>>heap;int n;cin>>n;for(int i=1;i<=n;i++){int a;cin>>a;heap.push(a);}int ans=0;while(heap.size()>1){int x1=heap.top();heap.pop();int x2=heap.top();heap.pop();ans+=x1+x2;heap.push(x1+x2);}cout<<ans<<endl;return 0;
}环形石子合并
将 n 堆石子绕圆形操场排放,现要将石子有序地合并成一堆。
规定每次只能选相邻的两堆合并成新的一堆,并将新的一堆的石子数记做该次合并的得分。
请编写一个程序,读入堆数 n 及每堆的石子数,并进行如下计算:
- 选择一种合并石子的方案,使得做 n−1次合并得分总和最大。
- 选择一种合并石子的方案,使得做 n−1 次合并得分总和最小。
输入格式
第一行包含整数 n,表示共有 n 堆石子。
第二行包含 n 个整数,分别表示每堆石子的数量。
输出格式
输出共两行:
第一行为合并得分总和最小值,
第二行为合并得分总和最大值。
数据范围
1≤n≤200
输入样例:
4
4 5 9 4
输出样例:
43
54 

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=440;
int f[N][N],g[N][N];
int w[N],s[N];
int main()
{int n;cin>>n;for(int i=1;i<=n;i++){cin>>w[i];w[i+n]=w[i];}for(int i=1;i<=2*n;i++) s[i]=s[i-1]+w[i];memset(f,0x3f,sizeof f);//求最小值 故初始化成大的memset(g,-0x3f,sizeof g);//求最大值 故初始化成小的for(int len=1;len<=n;len++){for(int i=1;i+len-1<=2*n;i++){int l=i,r=i+len-1;if(l==r){f[l][r]=0,g[l][r]=0;//只有自己一堆的时候 不需要花费}for(int k=l;k<r;k++){f[l][r]=min(f[l][r],f[l][k]+f[k+1][r]+s[r]-s[l-1]);g[l][r]=max(g[l][r],g[l][k]+g[k+1][r]+s[r]-s[l-1]);}}}int min1=0x3f3f3f3f,max1=-0x3f3f3f3f;for(int i=1;i<=n;i++){min1=min(min1,f[i][i+n-1]);max1=max(max1,g[i][i+n-1]);}cout<<min1<<endl<<max1<<endl;return 0;
}相关文章:

DP(区间DP)
石子合并 设有 N 堆石子排成一排,其编号为 1,2,3,…,N。 每堆石子有一定的质量,可以用一个整数来描述,现在要将这 N 堆石子合并成为一堆。 每次只能合并相邻的两堆,合并的代价为这两堆石子的质量之和,合并后与这两堆…...
MySQL5.7保姆级安装教程
环境 Linux版本Mysql版本(待安装)CentOS 75.7 1、配置YUM源 在MySQL官网中下载YUM源rpm安装包:http://dev.mysql.com/downloads/repo/yum/ 目前MySQL官网下载的MySQL源安装后yum下载的MySQL是8.0版本,为了非必要的麻烦,直接提供MySQL5.7的…...

Linux:getopts解析命令行选项和参数
一.背景 当自己编写多个shell脚本进行嵌套调用时,会涉及到传参数问题,此时可以通过getopts设置参数输入与变量赋值. 二.用法 当使用 getopts 命令来解析命令行选项和参数时,你需要在脚本中创建一个循环,循环中使用 getopts 命令来获取每个选项及其参数…...

c语言——三子棋
基本框架 三个文件: 其中.cpp文件用于游戏具体函数设计,.h文件为游戏的函数声明,test.cpp文件用于测试游戏运行。 需要用到的头文件: #include <stdio.h> #include <stdlib.h>//rand&srand #include <time.h>//时间相…...

Android 广播阻塞、延迟问题分析方法
一、问题 最近遇到一个问题,发送广播(普通广播)给另一个应用,但是广播需要要等约1min后才收到。 二、分析原因 原因是系统有个广播接收器在接收到广播后处理了接近50s,所以阻塞了后面的广播处理。如果大家也出现了广…...

HTML JS 解析器出sql 中 的所有表名称,支持多条SQL
<!DOCTYPE html> <html> <head><title>SQL表名提取器</title><script src"https://code.jquery.com/jquery-3.6.0.min.js"></script><script>function extractTableNames() {// 获取输入的SQL语句var sql document…...

【雕爷学编程】Arduino动手做(05)---热敏电阻模块之的基本参数、模块特色、电原理与使用说明
37款传感器与模块的提法,在网络上广泛流传,其实Arduino能够兼容的传感器模块肯定是不止37种的。鉴于本人手头积累了一些传感器和执行器模块,依照实践出真知(一定要动手做)的理念,以学习和交流为目的&#x…...

MS31860T 国产 8通道串行接口低边驱动器 可PIN TO PIN替代DRV8860 高性价比
MS31860T 国产 8通道串行接口低边驱动器 可PIN TO PIN替代DRV8860 高性价比 产品简述 MS31860T 是一款 8 通道低边驱动器,包含 SPI 串口通信、 PWM斩波器配置、过流保护、短路保护、欠压锁定和过热关断功能,芯片可以读取每个通道的状态。MS31860T 可以…...

百度 amis 当成 UI 库用
百度 amis 当成 UI 库用 1.获取到这些 amis 对外提供的方法 var amisLib amisRequire(amis);// 获取到这些 amis 对外提供的方法。 2.js中使用百度amis中 confirm amisLib.confirm(amisLib 是否确认).then((confirmed) > {if (confirmed) {// 用户确认后执行的操作consol…...
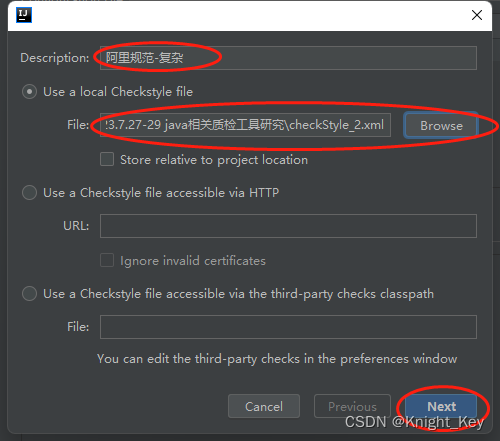
质检工具(FindBugs、CheckStyle、Junit、Jmeter、Apifox)
1、Findbugs IDEA软件中可以装该插件,2018版本以前主要搜索FindBugs-IDEA 、2018版本以后主要搜索 SpotBugs。 1.1、FindBugs-IDEA安装及使用流程: 1.2、SpotBugs安装及使用流程: 2、Checkstyle IDEA软件中可以装该插件,所有版本的插件一致:CheckStyle 2.1、安装流程…...

MS31803TE 国产 四通道低边驱动器 PIN对PIN替代DRV8803
MS31803TE 国产 四通道低边驱动器 PIN对PIN替代DRV8803 产品简述 MS31803TE 是一个具有过流保护功能的 4 通道低边驱动器。MS31803TE 内置钳位二极管,用来钳制由电感负载续流产生的电压。MS31803TE 可以驱动单极步进电机、直流电机、继电器、螺线管或者其它负载。…...
wordpress数据表中标签和分类如何区分?
wordpress中标签和分类是什么关系怎么区分?最后有一个群的网友告诉了我文章ID和标签ID的关系是放在了wp_term_relationships表中,然后我百度了下这个表的结构和相关介绍,发现果然如此,先把文章保存起来: wp_term_rela…...

css3 实现文字横幅无缝滚动
css3 实现文字横幅无缝滚动 使用 css3 关键帧 keyframes 和 animation 属性实现文字横幅无缝滚动。 <template><div class"skiHallBanner"><div class"skiHallBanner-text"><span>{{ text }}</span></div></div>…...
unity 修改默认脚本
using System.Collections; using System.Collections.Generic; using UnityEngine; //***************************************** //创建人: xxxx //功能说明: //***************************************** #ROOTNAMESPACEBEGIN# public class #SCRI…...
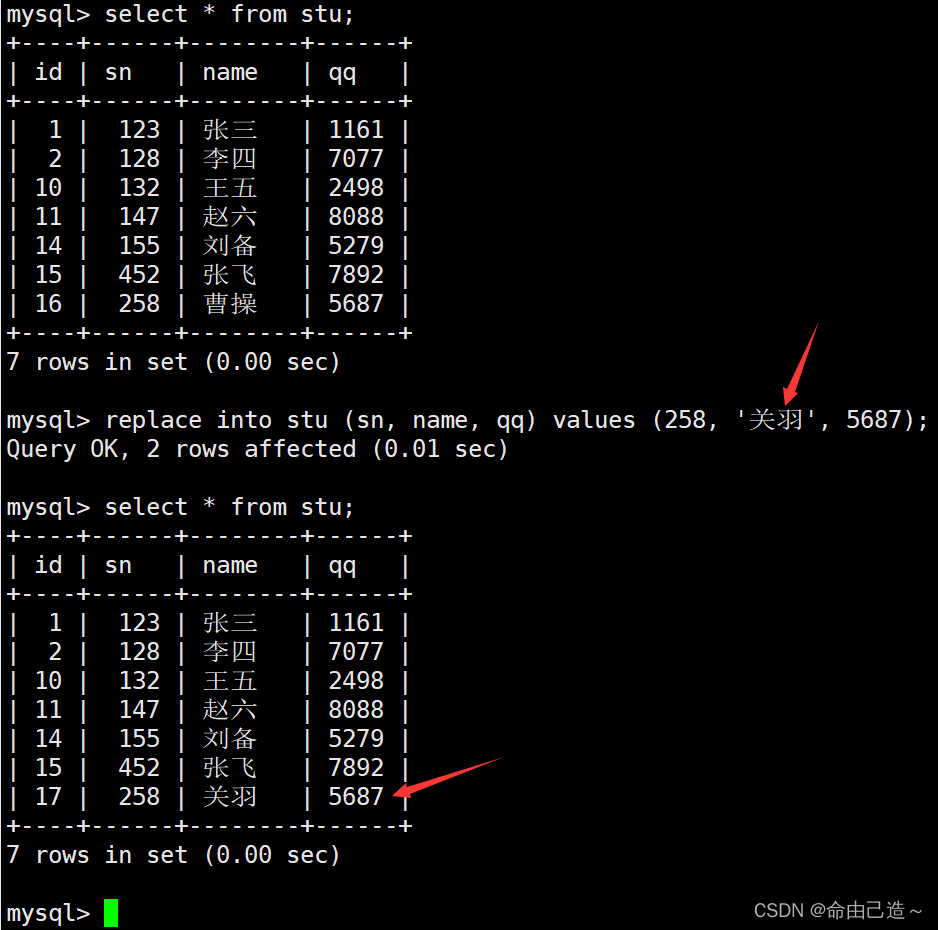
【MySQL】增删查改基础
文章目录 一、创建操作1.1 单行插入1.2 多行插入1.3 插入否则替换更新1.4 替换replace 二、查询操作2.1 select查询2.2 where条件判断2.3 order by排序2.4 limit筛选分页结果 三、更新操作四、删除操作4.1 删除一列4.2 删除整张表数据 五、插入查询结果 CRUD : Create(创建), R…...
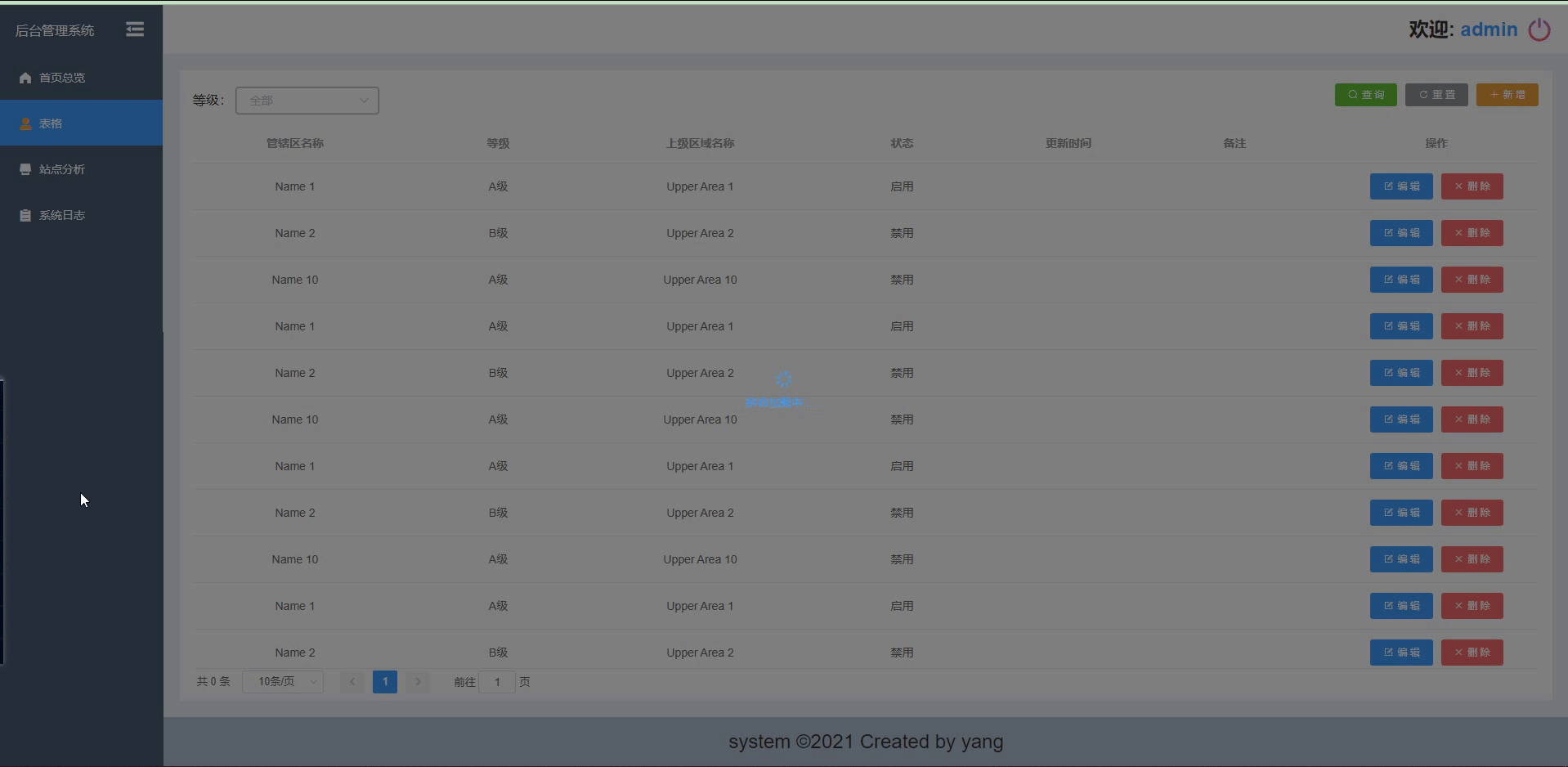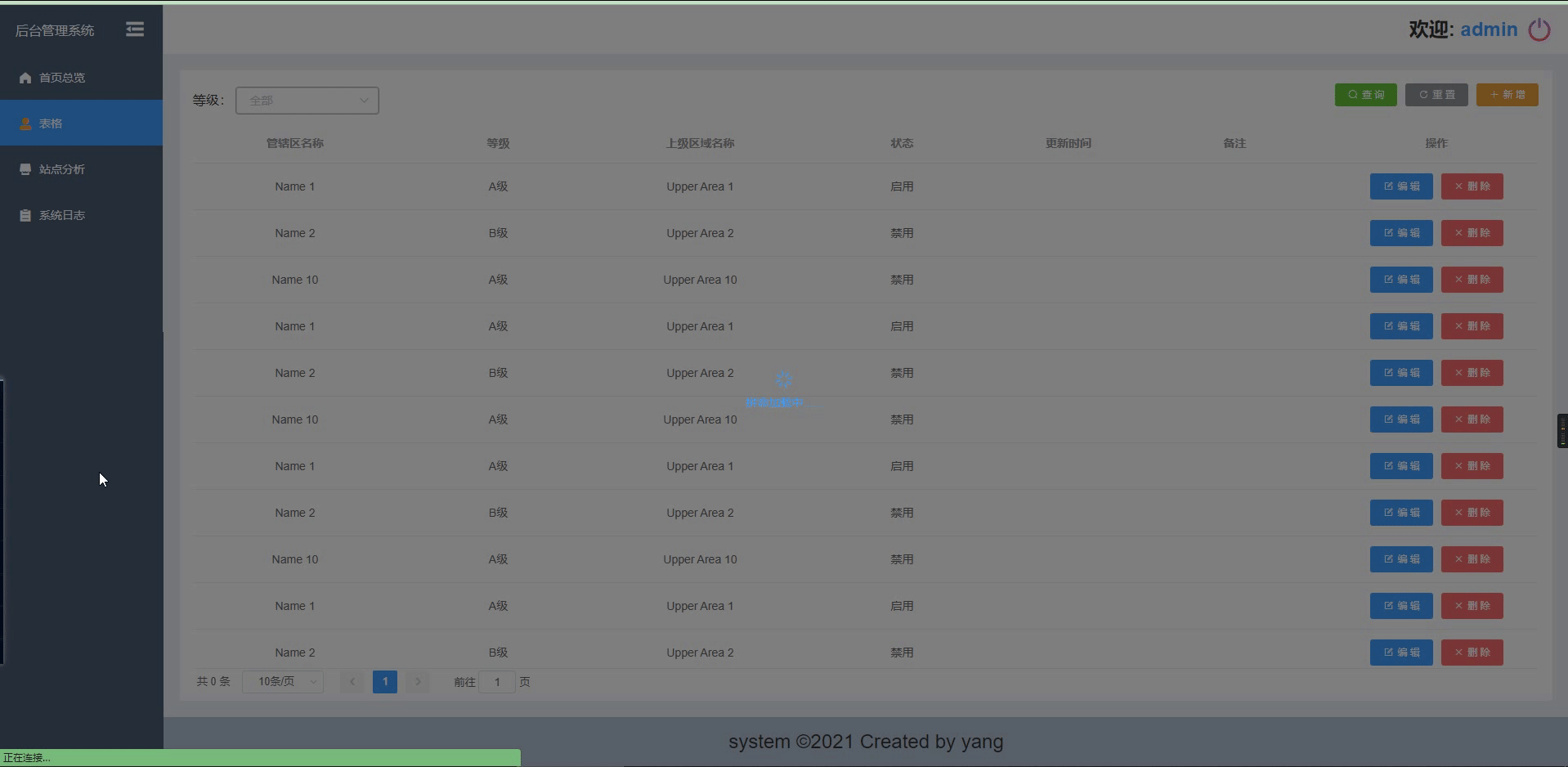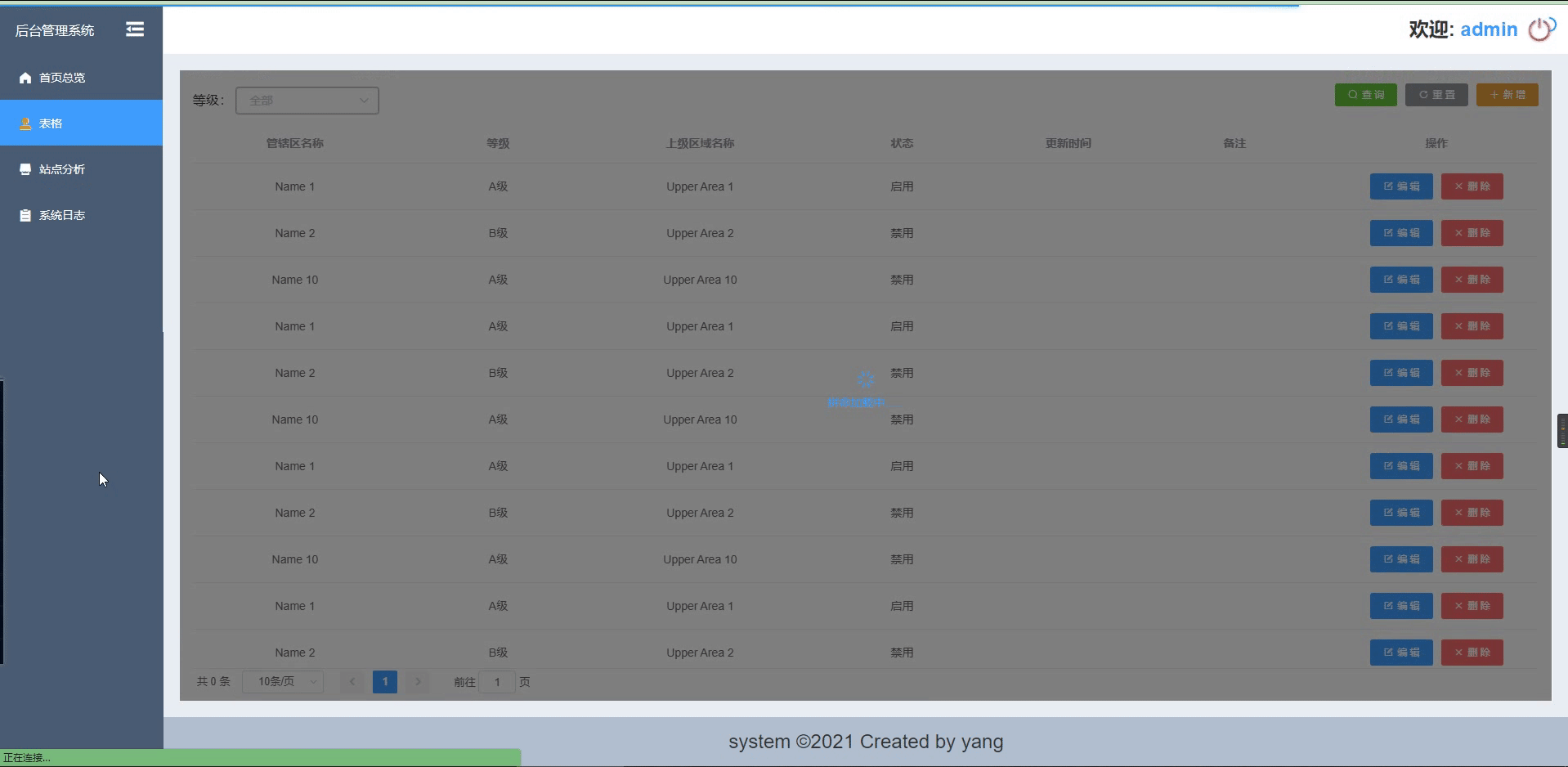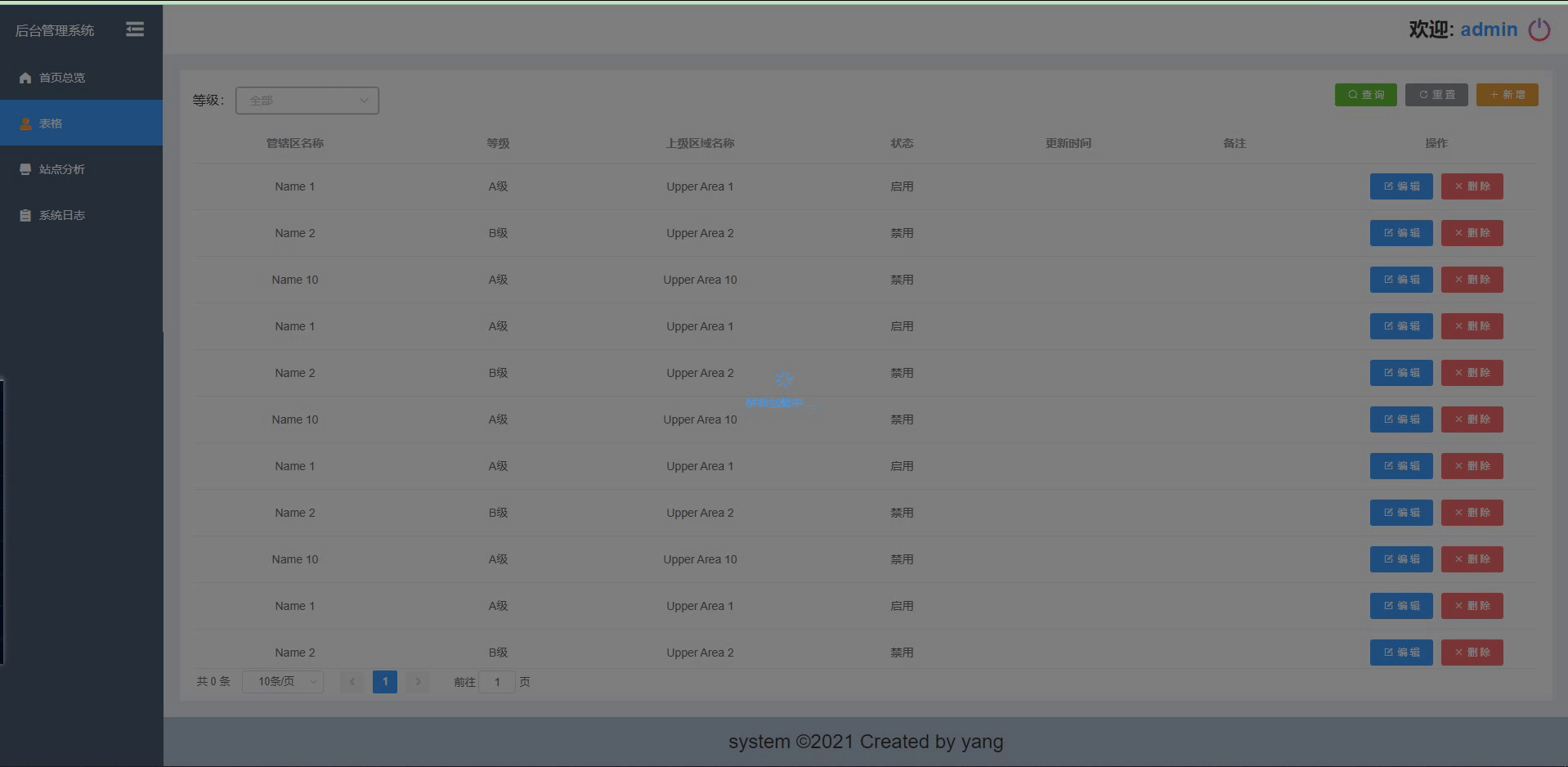
【vue+el-table+el-backtop】表格结合返回顶部使用,loading局部加载
效果图: 一. 表格结合返回顶部 二. 局部loading 解决方法: 一 返回顶部 target绑定滚动dom的父元素类名就可以了. 1.如果你的表格是 固定表头 的,那滚动dom的父元素类名就是 el-table__body-wrapper <el-backtop target".el-table__body-wrapper" :visibility…...
设计模式(4)装饰模式
一、介绍: 1、应用场景:把所需的功能按正确的顺序串联起来进行控制。动态地给一个对象添加一些额外的职责,就增加功能来说,装饰模式比生成子类更加灵活。 当需要给一个现有类添加附加职责,而又不能采用生成子类的方法…...
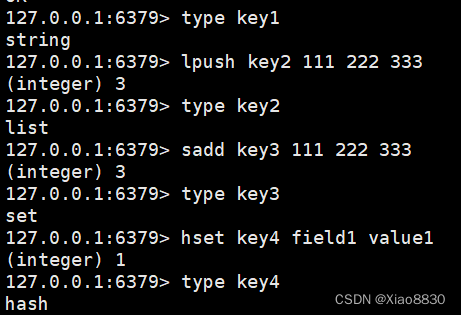
Redis——通用命令介绍
Redis官方文档 redis官方文档 核心命令 set 将key和value存储到Redis中,key和value都是字符串 set key valueRedis中不区分大小写,字符串类型也不需要添加单引号或者双引号 get 根据key读取value,如果当前key不存在,则返回…...

EmberJS教程_编程入门自学教程_菜鸟教程-免费教程分享
教程简介 Ember.js 是一个开源 JavaScript框架,用于开发基于模型-视图-控制器( MVC)架构的大型客户端 Web 应用程序。 Ember 旨在减少开发时间和提高生产力,它是全球采用的增长最快的前端应用程序框架之一。它目前在许多网站上使用,例如 Squ…...

Diffusion扩散模型学习4——Stable Diffusion原理解析-inpaint修复图片为例
Diffusion扩散模型学习4——Stable Diffusion原理解析-inpaint修复图片为例 学习前言源码下载地址原理解析一、先验知识二、什么是inpaint三、Stable Diffusion中的inpaint1、开源的inpaint模型2、基于base模型inpaint 四、inpaint流程1、输入图片到隐空间的编码2、文本编码3、…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...

tomcat入门
1 tomcat 是什么 apache开发的web服务器可以为java web程序提供运行环境tomcat是一款高效,稳定,易于使用的web服务器tomcathttp服务器Servlet服务器 2 tomcat 目录介绍 -bin #存放tomcat的脚本 -conf #存放tomcat的配置文件 ---catalina.policy #to…...

Spring AI Chat Memory 实战指南:Local 与 JDBC 存储集成
一个面向 Java 开发者的 Sring-Ai 示例工程项目,该项目是一个 Spring AI 快速入门的样例工程项目,旨在通过一些小的案例展示 Spring AI 框架的核心功能和使用方法。 项目采用模块化设计,每个模块都专注于特定的功能领域,便于学习和…...
