扩散模型diffusion model用于图像恢复任务详细原理 (去雨,去雾等皆可),附实现代码
文章目录
- 1. 去噪扩散概率模型
- 2. 前向扩散
- 3. 反向采样
- 3. 图像条件扩散模型
- 4. 可以考虑改进的点
- 5. 实现代码
1. 去噪扩散概率模型
扩散模型是一类生成模型, 和生成对抗网络GAN 、变分自动编码器VAE和标准化流模型NFM等生成网络不同的是, 扩散模型在前向扩散过程中对图像逐步施加噪声, 直至图像被破坏变成完全的高斯噪声, 然后在反向采样过程中学习从高斯噪声还原为真实图像。在模型训练完成后,只需要随机给定一个高斯噪声,就可以生成丰富的真实图像。

2. 前向扩散
前向扩散过程就是向图像不断加高斯噪声,使其逐渐接近一个与输入数据相关的高斯分布。此处将未加噪声的数据记为x0x_0x0,x0∼q(x0)x_0\sim q(x_0)x0∼q(x0),q(x0)q(x_0)q(x0)是为被噪声破坏的原始数据分布,则在ttt时刻的噪化状态和上一时刻t−1t-1t−1之间的关系为:
q(xt∣xt−1)=N(xt;1−βt⋅xt−1,βt⋅I),(1)q(x_t|x_{t-1})=\mathcal{N}(x_t; \sqrt{1-\beta_t}\cdot x_{t-1}, \beta_t\cdot\textbf{I}), \tag{1}q(xt∣xt−1)=N(xt;1−βt⋅xt−1,βt⋅I),(1)其中:t∈{0,1,...,T}t\in{\{0, 1, ..., T\}}t∈{0,1,...,T},N\mathcal{N}N表示高斯噪声分布,βt\beta_tβt是与时刻t相关的噪声方差调节因子,I\textbf{I}I是一个与初始状态x0x_0x0维度相同的单位矩阵。则输入x0x_0x0的条件下,x1,x2,...,xTx_1, x_2, ..., x_Tx1,x2,...,xT的联合分布可以表示为:
q(x1,x2,...,xT∣x0)=∏t=1Tq(xt∣xt−1)(2)q(x_1, x_2, ..., x_T|x_0)=\displaystyle\prod_{t=1}^{T}q(x_t|x_{t-1}) \tag{2}q(x1,x2,...,xT∣x0)=t=1∏Tq(xt∣xt−1)(2)则根据根据马尔科夫性可以直接得到输入x0x_0x0的条件下ttt时刻的噪化状态为
q(xt∣x0)=N(xt;α‾t⋅x0,(1−α‾t)⋅I),(3)q(x_t|x_0)=\mathcal{N}(x_t; \sqrt{\overline{\alpha}_t}\cdot x_0, (1-\overline{\alpha}_t)\cdot\textbf{I}), \tag{3}q(xt∣x0)=N(xt;αt⋅x0,(1−αt)⋅I),(3)其中:αt:=1−βt\alpha_t:=1-\beta_tαt:=1−βt, α‾t:=∏s=0tαs\overline{\alpha}_t:=\prod_{s=0}^{t}\alpha_sαt:=∏s=0tαs。根据公式(1)(1)(1)可以得到ttt时刻的噪化状态xtx_txt与t−1t-1t−1时刻的噪化状态xt−1x_{t-1}xt−1的关系为:
xt=αt⋅xt−1+1−αt⋅ϵt−1,(4)x_t=\sqrt{\alpha_t}\cdot x_{t-1}+\sqrt{1-\alpha_t}\cdot\epsilon_{t-1}, \tag{4}xt=αt⋅xt−1+1−αt⋅ϵt−1,(4)其中:ϵt−1∼N(0,I)\epsilon_{t-1}\sim\mathcal{N}(\textbf{0}, \textbf{I})ϵt−1∼N(0,I),通过不断取代递推可以得到ttt时刻的噪化状态xtx_txt与输入x0x_0x0之间的关系为:
xt=αt⋅xt−1+1−αt⋅ϵt−1=αtαt−1⋅xt−2+1−αtαt−1⋅ϵ‾t−2=αtαt−1αt−2⋅xt−3+1−αtαt−1αt−2⋅ϵ‾t−3…=α‾t⋅x0+1−α‾t⋅ϵ(5)\begin{equation*} \begin{aligned} x_t & = \sqrt{\alpha_t}\cdot x_{t-1}+\sqrt{1-\alpha_t}\cdot\epsilon_{t-1} \\ ~ & = \sqrt{\alpha_t\alpha_{t-1}}\cdot x_{t-2}+\sqrt{1-\alpha_t\alpha_{t-1}}\cdot\overline{\epsilon}_{t-2} \\ ~ & = \sqrt{\alpha_t\alpha_{t-1}\alpha_{t-2}}\cdot x_{t-3}+\sqrt{1-\alpha_t\alpha_{t-1}\alpha_{t-2}}\cdot\overline{\epsilon}_{t-3} \\ ~ & \dots \\ ~ & = \sqrt{\overline{\alpha}_t}\cdot x_0+\sqrt{1-\overline{\alpha}_t}\cdot\epsilon \\ \end{aligned} \end{equation*} \tag{5} xt =αt⋅xt−1+1−αt⋅ϵt−1=αtαt−1⋅xt−2+1−αtαt−1⋅ϵt−2=αtαt−1αt−2⋅xt−3+1−αtαt−1αt−2⋅ϵt−3…=αt⋅x0+1−αt⋅ϵ(5)其中:ϵ∼N(0,I)\epsilon\sim\mathcal{N}(\textbf{0}, \textbf{I})ϵ∼N(0,I), ϵ‾t−2\overline{\epsilon}_{t-2}ϵt−2是两个高斯分布相加后的分布。第一步到第二步的公式推导需要说明一下,根据高斯噪声的特点,对于两个方差不同的高斯分布N(0,σ12⋅I)\mathcal{N}(\textbf{0}, \sigma_1^2\cdot\textbf{I})N(0,σ12⋅I)和N(0,σ22⋅I)\mathcal{N}(\textbf{0}, \sigma_2^2\cdot\textbf{I})N(0,σ22⋅I),其相加后的高斯分布为N(0,(σ12+σ22)⋅I)\mathcal{N}(\textbf{0}, (\sigma_1^2+\sigma_2^2)\cdot\textbf{I})N(0,(σ12+σ22)⋅I),表现在公式中,即:
xt=αt⋅xt−1+1−αt⋅ϵt−1=αt⋅(αt−1⋅xt−2+1−αt−1⋅ϵt−2)+1−αt⋅ϵt−1=αtαt−1⋅xt−2+αt(1−αt−1)⋅ϵt−2+1−αt⋅ϵt−1=αtαt−1⋅xt−2+1−αtαt−1⋅ϵ‾t−2(6)\begin{equation} \begin{aligned} x_t & = \sqrt{\alpha_t}\cdot x_{t-1}+\sqrt{1-\alpha_t}\cdot\epsilon_{t-1} \\ ~ & = \sqrt{\alpha_t}\cdot( \sqrt{\alpha_{t-1}}\cdot x_{t-2}+\sqrt{1-\alpha_{t-1}}\cdot\epsilon_{t-2})+\sqrt{1-\alpha_t}\cdot\epsilon_{t-1} \\ ~ & = \sqrt{\alpha_t\alpha_{t-1}}\cdot x_{t-2}+ \sqrt{\alpha_t(1-\alpha_{t-1})}\cdot\epsilon_{t-2}+\sqrt{1-\alpha_t}\cdot\epsilon_{t-1} \\ ~ & = \sqrt{\alpha_t\alpha_{t-1}}\cdot x_{t-2}+\sqrt{1-\alpha_t\alpha_{t-1}}\cdot\overline{\epsilon}_{t-2} \end{aligned} \end{equation} \tag{6} xt =αt⋅xt−1+1−αt⋅ϵt−1=αt⋅(αt−1⋅xt−2+1−αt−1⋅ϵt−2)+1−αt⋅ϵt−1=αtαt−1⋅xt−2+αt(1−αt−1)⋅ϵt−2+1−αt⋅ϵt−1=αtαt−1⋅xt−2+1−αtαt−1⋅ϵt−2(6)其中:两个高斯分布相加后的标准差为:
αt(1−αt−1)+(1−αt)=1−αtαt−1,(7)\sqrt{\alpha_t(1-\alpha_{t-1})+(1-\alpha_t)}=\sqrt{1-\alpha_t\alpha_{t-1}}, \tag{7}αt(1−αt−1)+(1−αt)=1−αtαt−1,(7)依此得到第二步,进而逐渐递推到最后一步。公式(3)(3)(3)和公式(5)(5)(5)的目的就是表明在前向扩散过程中,由于每步加的噪声均是同分布的高斯噪声,因此不需要逐步进行加噪,直接就可以由输入x0x_0x0的到TTT时刻的噪化状态xTx_TxT。当α‾T≈0\overline{\alpha}_T\approx0αT≈0,TTT时刻的分布xtx_txt则几乎就是一个高斯分布,据此其可以定义为:
q(xT):=∫q(xT∣x0)q(x0)dx0≈N(xT;0,I),(5)q(x_T):=\int q(x_T|x_0)q(x_0)dx_0\approx\mathcal{N}(x_T; \textbf{0}, \textbf{I}), \tag{5}q(xT):=∫q(xT∣x0)q(x0)dx0≈N(xT;0,I),(5)其中:∫\int∫表示积分,最终的噪化状态xTx_TxT也可以在图像上看出其分布特点。

3. 反向采样
反向采样过程就是根据已有的噪化状态通过学习来估计噪声分布,进一步获得上一时刻的状态,并逐渐从高斯分布中构造出真实数据。根据前向扩散过程的结果,可以认为TTT时刻噪化状态xTx_TxT的后验分布p(xt)∼N(xt;0,I)p(x_t)\sim\mathcal{N}(x_t; \textbf{0}, \textbf{I})p(xt)∼N(xt;0,I),则联和分布pθ(x0,x1,...,xT)p_{\theta}(x_0, x_1, ..., x_T)pθ(x0,x1,...,xT)也是一个马尔科夫链,其被定义为:
pθ(x0,x1,...,xT):=p(xT)∏t=1Tpθ(xt−1∣xt),(6)p_{\theta}(x_0, x_1, ..., x_T):=p(x_T)\displaystyle\prod_{t=1}^{T}p_{\theta}(x_{t-1}|x_t), \tag{6}pθ(x0,x1,...,xT):=p(xT)t=1∏Tpθ(xt−1∣xt),(6)则t−1t-1t−1时刻的噪状态xt−1x_{t-1}xt−1可以由上一时刻ttt的状态xtx_txt得到,其条件分布可以表示为:
pθ(xt−1∣xt)=N(xt−1;μθ(xt,t),∑θ(xt,t)),(7)p_{\theta}(x_{t-1}|x_t)=\mathcal{N}(x_{t-1}; \mu_{\theta}(x_t, t), {\tiny{\sum}}_{\theta}(x_t, t)), \tag{7}pθ(xt−1∣xt)=N(xt−1;μθ(xt,t),∑θ(xt,t)),(7)其中:μθ(xt,t)\mu_\theta(x_t, t)μθ(xt,t)和∑θ(xt,t)){\tiny{\sum}}_{\theta}(x_t, t))∑θ(xt,t))分别为ttt时刻由噪声估计网络得到的噪声均值和方差,θ\thetaθ为噪声估计网络的参数。此时,在输入为x0x_0x0时,t−1t-1t−1时刻的噪状态xt−1x_{t-1}xt−1与上一时刻ttt的状态xtx_txt之间的真实条件分布为:
q(xt−1∣xt,x0)=N(xt−1;μ~t(xt,x0),β~t⋅I),(8)q(x_{t-1}|x_t, x_0)=\mathcal{N}(x_{t-1}; \tilde{\mu}_{t}(x_t, x_0), \tilde{\beta}_t\cdot\textbf{I}), \tag{8}q(xt−1∣xt,x0)=N(xt−1;μ~t(xt,x0),β~t⋅I),(8)其中:噪声后验分布参数μ~t\widetilde{\mu}_tμt, β~t\tilde{\beta}_tβ~t分别为:
μ~t=1αt(xt−βt1−α‾t⋅ϵt),β~t=1−α‾t−11−α‾t⋅βt,(9)\tilde{\mu}_t=\frac{1}{\sqrt{\alpha_t}}(x_t-\frac{\beta_t}{\sqrt{1-\overline{\alpha}_t}}\cdot\epsilon_t), \tilde{\beta}_t=\frac{1-\overline{\alpha}_{t-1}}{1-\overline{\alpha}_t}\cdot\beta_t, \tag{9}μ~t=αt1(xt−1−αtβt⋅ϵt),β~t=1−αt1−αt−1⋅βt,(9)此处认为∑θ(xt,t)=σt2⋅I{\small{\sum}}_\theta(x_t, t)=\sigma_t^2\cdot\textbf{I}∑θ(xt,t)=σt2⋅I,即σt2=β~t\sigma_t^2=\tilde{\beta}_tσt2=β~t,则预测的后验条件分布变为:
pθ(xt−01∣xt)=N(xt−1;μθ(xt,t),σt2⋅I),,(10)p_{\theta}(x_{t-01}|x_t)=\mathcal{N}(x_{t-1}; \mu_\theta(x_t, t), \sigma_t^2\cdot\textbf{I}), \tag{10}, pθ(xt−01∣xt)=N(xt−1;μθ(xt,t),σt2⋅I),,(10)即利用噪声估计网络μθ\mu_\thetaμθ来估计真实噪声分布均值μ~t\tilde{\mu}_tμ~t,则公式(9)(9)(9)中的噪声分布均值可以被估计为:
μθ(xt,t)=1αt(xt−βt1−α‾t⋅ϵθ(xt,t)),(11)\mu_\theta(x_t, t)=\frac{1}{\sqrt{\alpha_t}}(x_t-\frac{\beta_t}{\sqrt{1-\overline{\alpha}_t}}\cdot\epsilon_\theta(x_t, t)), \tag{11}μθ(xt,t)=αt1(xt−1−αtβt⋅ϵθ(xt,t)),(11)而根据公式已知ttt时刻的噪化状态xtx_txt满足xt=α‾t⋅x0+1−α‾t⋅ϵx_t=\sqrt{\overline{\alpha}_t}\cdot x_0+\sqrt{1-\overline{\alpha}_t}\cdot\epsilonxt=αt⋅x0+1−αt⋅ϵ,则网络学习的优化目标就是让估计出的噪声分布接近真实的噪声分布,即:
Ex0,t,ϵt∼N(0,I)[∣∣ϵt−ϵθ(α‾t⋅x0+1−α‾t⋅ϵ,t)∣∣2],(12)\mathbb{E}_{x_0, t, \epsilon_t\sim\mathcal{N}(0, \textbf{I})}[||\epsilon_t-\epsilon_\theta(\sqrt{\overline\alpha}_t\cdot x_0+\sqrt{1-\overline{\alpha}_t}\cdot\epsilon, t)||^2], \tag{12}Ex0,t,ϵt∼N(0,I)[∣∣ϵt−ϵθ(αt⋅x0+1−αt⋅ϵ,t)∣∣2],(12)而t−1t-1t−1时刻的噪化状态xt−1x_{t-1}xt−1可以表示为 (这块尚没搞清楚这个公式的由来,似乎与原论文中的公式不一样):
xt−1=α‾t−1(xt−1−α‾t⋅ϵθ(xt,t)α‾t)+1−α‾t−1⋅ϵθ(xt,t),(13)x_{t-1}=\sqrt{\overline\alpha_{t-1}}(\frac{x_t-\sqrt{1-\overline{\alpha}_t}\cdot\epsilon_\theta(x_t, t)}{\sqrt{\overline{\alpha}_t}})+\sqrt{1-\overline{\alpha}_{t-1}}\cdot\epsilon_\theta(x_t, t), \tag{13}xt−1=αt−1(αtxt−1−αt⋅ϵθ(xt,t))+1−αt−1⋅ϵθ(xt,t),(13)其中:z∼N(0,I)z\sim\mathcal{N}(\textbf{0}, \textbf{I})z∼N(0,I)。则根据不同时刻噪声估计网络对噪声分布的估计可以依据公式(13)(13)(13)逐渐反向采样得到真实数据分布。

3. 图像条件扩散模型
在图像恢复任务中,必须使用条件扩散模型才能生成我们预期的恢复图像,实际中即将退化的图像作为条件引入到噪声估计网络中来估计条件噪声分布。如图所示:

图像条件扩散模型与经典扩散模型的前向扩散过程完全一样,区别仅在于反向采样过程中是否引入图像条件。则反向采样过程中x1,x2,...,xTx_1, x_2, ..., x_Tx1,x2,...,xT的联合分布变为:
pθ(x0,x1,...,xT∣x^):=p(xT)∏t=1Tpθ(xt−1∣xt,x^),(14)p_{\theta}(x_0, x_1, ..., x_T|\hat{x}):=p(x_T)\displaystyle\prod_{t=1}^{T}p_{\theta}(x_{t-1}|x_t, \hat{x}), \tag{14}pθ(x0,x1,...,xT∣x^):=p(xT)t=1∏Tpθ(xt−1∣xt,x^),(14)其中,x^\hat{x}x^为作为条件输入噪声估计网络的退化图像。此时,噪声分布估计变为:
ϵθ(xt,t)→ϵθ(xt,x^,t),(15)\epsilon_\theta(x_t, t)\rightarrow\epsilon_\theta(x_t, \hat{x}, t), \tag{15}ϵθ(xt,t)→ϵθ(xt,x^,t),(15)t−1t-1t−1时刻的噪化状态xt−1x_{t-1}xt−1也由公式(13)(13)(13)变为:
xt−1=α‾t−1(xt−1−α‾t⋅ϵθ(xt,x^,t)α‾t)+1−α‾t−1⋅ϵθ(xt,x^,t),(16)x_{t-1}=\sqrt{\overline\alpha_{t-1}}(\frac{x_t-\sqrt{1-\overline{\alpha}_t}\cdot\epsilon_\theta(x_t, \hat{x}, t)}{\sqrt{\overline{\alpha}_t}})+\sqrt{1-\overline{\alpha}_{t-1}}\cdot\epsilon_\theta(x_t, \hat{x}, t), \tag{16}xt−1=αt−1(αtxt−1−αt⋅ϵθ(xt,x^,t))+1−αt−1⋅ϵθ(xt,x^,t),(16)
实际中,条件的引入由多种方式,最常见的方法是直接通过与噪化状态拼接后作为噪声估计网络的输入。
4. 可以考虑改进的点
以下是我问chatGPT得到的答案:

我的拙见:
- 引入天气退化图像恢复中:虽然扩散模型已经出现众多研究,但在图像去雨、去雾、去雨滴、去雪等方面的研究屈指可数;
- 改进噪声估计网络:经典的扩散模型是基于U-Net结构的,主要模块也是卷积 (也包括自注意力),近来有一些研究发现Transformer架构在扩散模型上可以取得更好地效果;
- Follow最新的更快地扩散模型:传统的扩散模型要进行图像恢复,一幅图片的处理时长基本都是几十秒,实时性太差,目前有一些研究提出快速反向采样的方法;
- 无监督:目前多数给予扩散模型的图像恢复算法仍然是有监督的 (当然不算是监督学习,只是条件生成),可以采用一些无监督策略来利用扩散模型实现图像恢复。
5. 实现代码
完整的用于图像恢复的扩散模型代码见:完整可直接运行代码,其中包括详细的实验操作流程,只需要修改数据集路径即可直接使用。

相关文章:

扩散模型diffusion model用于图像恢复任务详细原理 (去雨,去雾等皆可),附实现代码
文章目录1. 去噪扩散概率模型2. 前向扩散3. 反向采样3. 图像条件扩散模型4. 可以考虑改进的点5. 实现代码1. 去噪扩散概率模型 扩散模型是一类生成模型, 和生成对抗网络GAN 、变分自动编码器VAE和标准化流模型NFM等生成网络不同的是, 扩散模型在前向扩散过程中对图像逐步施加噪…...
pytorch
PyTorch基础 import torch torch.__version__ #return 1.13.1cu116基本使用方法 矩阵 x torch.empty(5, 3)tensor([[1.4586e-19, 1.1578e27, 2.0780e-07],[6.0542e22, 7.8675e34, 4.6894e27],[1.6217e-19, 1.4333e-19, 2.7530e12],[7.5338e28, 8.1173e-10, 4.3861e-43],[2.…...

软件测试—对职业生涯发展的一些感想
目录:导读 职场生涯 1、短期规划 2、长期规划 自身定位 1、你在哪儿? 2、你想要什么? 3、你拥有什么? 4、你需要做什么?什么时候做? 5、淡定啊淡定 最近工作不是很忙,有空都是在看书&a…...
5年经验之谈:月薪3000到30000,测试工程师的变“行”记!
自我介绍下,我是一名转IT测试人,我的专业是化学,去化工厂实习才发现这专业的坑人之处,化学试剂害人不浅,有毒,易燃易爆,实验室经常用丙酮,甲醇,四氯化碳,接触…...
全价值链赋能,数字化助力营销价值全力释放 | 爱分析报告
报告编委 张扬 爱分析联合创始人&首席分析师 文鸿伟 爱分析高级分析师 王鹏 爱分析分析师 外部专家(按姓氏拼音排序) 黄洵 客易达 联合创始人 毛健 云徙科技 副总裁 & COO 特别鸣谢(按拼音排序) 报告摘要 在…...

【自学Docker 】Docker search命令
大纲 Docker search命令 docker search命令教程 docker search 命令用于从 Docker Hub 查找镜像。 docker search命令语法 haicoder(www.haicoder.net)# docker search [OPTIONS] TERMdocker search命令参数 参数描述docker search --filter设置过滤条件。docker search -…...
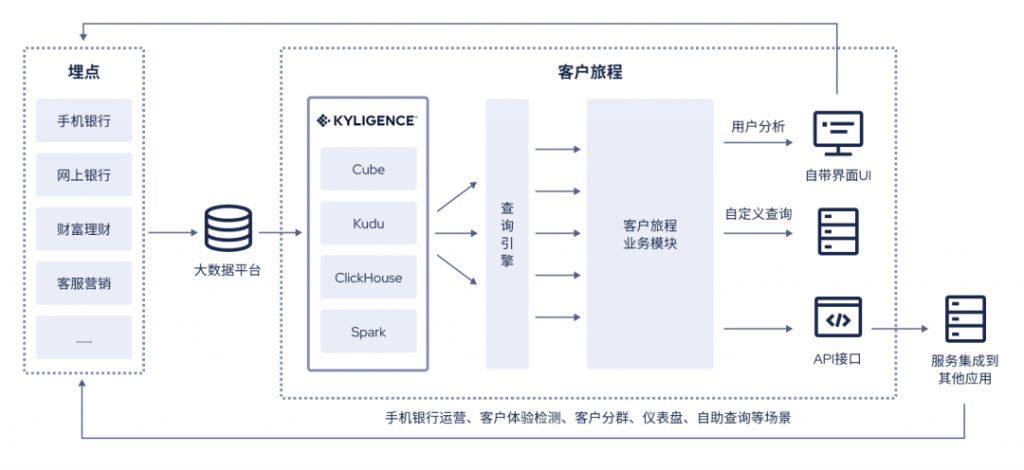
银行零售如何更贴近客户?是时候升级你的客户旅程平台了
随着数字化战略推进,各大银行持续加大对线上多渠道的建设投入,客户触达也愈发移动化、智能化。与此同时,手机银行飞速发展产生并累积了大量客户行为数据,呈多样化、海量化等特点,将在用户体验、客户经营、手机银行运营…...
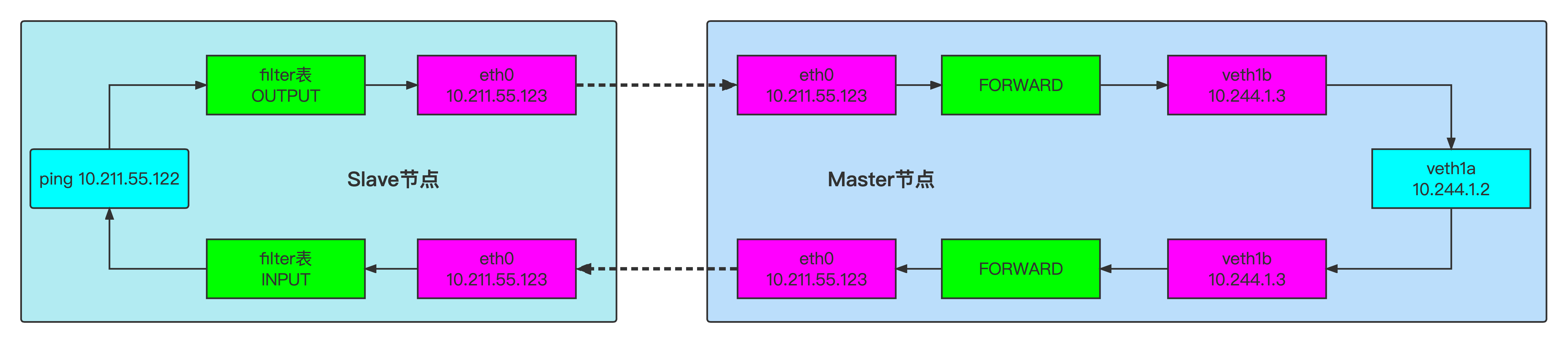
零入门kubernetes网络实战-12->基于DNAT技术使得外网可以访问本宿主机上veth-pair链接的内部网络
视频地址(稍后上传) 本篇文章测试如何让veth pair链接的内网网络可以被本局域网的其他宿主机访问到? 1、测试环境介绍 一台centos虚拟机 # 查看操作系统版本 cat /etc/centos-release # 内核版本 uname -a uname -r # 查看网卡信息 ip a s eth02、网络拓扑 3、操…...

conda环境管理命令
conda环境管理命令 1.环境检查 1)查看安装了哪些包 conda list 2)查看当前存在哪些虚拟环境 conda env list conda info -e [rootoracledb anaconda3]# conda info -e # conda environments: # base * /home/anaconda33)检查更新当前conda con…...
ubuntu clion从0开始搭建一个风格转换ONNX推理网络 opencv cuda::dnn::net
系统搭建 系统搭建 OpenCV的安装 cmake sudo apt-get install cmake其他环境以来 sudo apt-get install build-essential libgtk2.0-dev libavcodec-dev libavformat-dev libjpeg.dev libtiff5.dev libswscale-dev libjasper-dev 不安装会报这个错误 OpenCV(4.6.0) /hom…...

1.十大排序算法
1.什么是排序算法? 在梳理十大排序算法之前,虽然知道排序算法是将数字或字母按增序排列的算法,但该理解过于片面,那排序算法的权威定义是什么呢。 一个排序算法(英语:Sorting algorithm)是一种…...
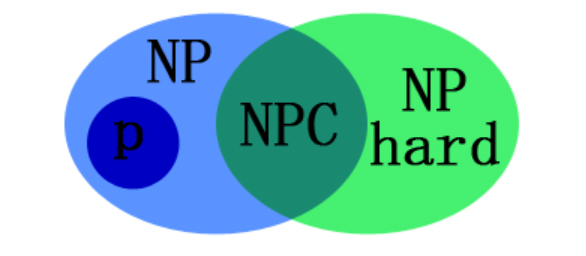
算法导论—SAT、NP、NPC、NP-Hard问题
算法导论—SAT、NP、NP-Hard、NPC问题SAT 问题基本定义问题复杂性P、NP、NP-Hard、NP-Complete(NPC)证明NP-Hard关系图NP问题的概念约化的定义NPC问题NP-Hard问题SAT 问题基本定义 SAT 问题 (Boolean satisfiability problem, 布尔可满足性问题,SAT): 给…...

linux入门---基础指令(上)
这里写目录标题前言ls指令pwd指令cd指令touch指令mkdirrmdirrmman指令cp指令mv指令前言 我们平时使用电脑主要是通过鼠标键盘以及操作系统中自带的图形来对电脑执行相应的命令,比如说我想打开D盘中的cctalk这个文件: 我就可以先用鼠标左键单击这个文件…...
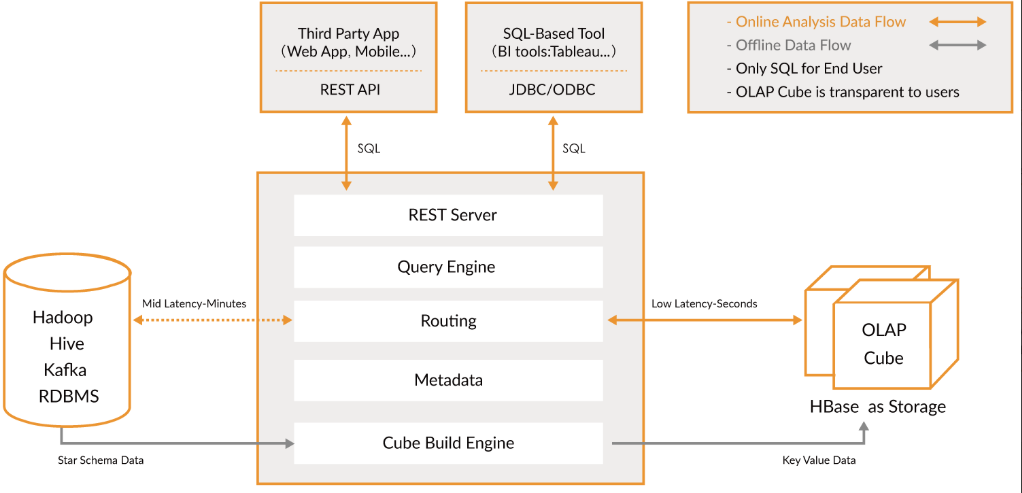
大数据Kylin(一):基础概念和Kylin简介
文章目录 基础概念和Kylin简介 一、OLTP与OLAP 1、OLTP 2、OLAP 3、OLTP与OLAP的关系 二、数据分析模型 1、星型模型 2、雪花模型 …...

推进行业生态发展完善,中国信通院第八批RPA评测工作正式启动
随着人工智能、云计算、大数据等新兴数字技术的高速发展,数字劳动力应用实践步伐加快,以数字生产力、数字创造力为基础的数字经济占比逐年上升。近年来,机器人流程自动化(Robotic Process Automation,RPA)成…...

DOM编程-获取下拉列表选中项的value
<!DOCTYPE html> <html> <head> <meta charset"utf-8"> <title>获取下拉列表选中项的value</title> </head> <body> <script type"text/javascript"> …...

认证服务-----技术点及亮点
大技术Nacos做注册中心把新建的微服务注册到Nacos上去两个步骤 在配置文件中配置应用名称、nacos的发现注册ip地址,端口号在启动类上用EnableDiscoveryClient注解开启注册功能使用Redis存验证码信息加入依赖配置地址和端口号即可直接注入StringRedisTemplate模板类用…...
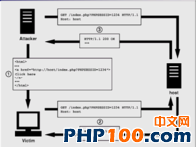
6个常见的 PHP 安全性攻击
了解常见的PHP应用程序安全威胁,可以确保你的PHP应用程序不受攻击。因此,本文将列出 6个常见的 PHP 安全性攻击,欢迎大家来阅读和学习。 1、SQL注入 SQL注入是一种恶意攻击,用户利用在表单字段输入SQL语句的方式来影响正常的SQL执…...
三大基础排序算法——冒泡排序、选择排序、插入排序
目录前言一、排序简介二、冒泡排序三、选择排序四、插入排序五、对比References前言 在此之前,我们已经介绍了十大排序算法中的:归并排序、快速排序、堆排序(还不知道的小伙伴们可以参考我的 「数据结构与算法」 专栏)࿰…...
负载均衡上传webshell+apache换行解析漏洞
目录一、负载均衡反向代理下的webshell上传1、nginx负载均衡2、负载均衡下webshell上传的四大难点难点一:需要在每一台节点的相同位置上传相同内容的webshell难点二:无法预测下一次请求是哪一台机器去执行难点三:当我们需要上传一些工具时&am…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...
