数据结构~七大排序算法(Java实现)
目录
插入排序
直接插入排序
希尔排序
选择排序
直接选择排序
堆排序
交换排序
冒泡排序
快速排序
递归实现
优化版本
归并排序
插入排序
直接插入排序
public class MySort {public static void insertSort(int[] array) {for (int i = 1; i < array.length; i++) {int j = i - 1;int tmp = array[i];for (; j >= 0; j--) {if (tmp < array[j]) {array[j + 1] = array[j];} else {break;}}array[j + 1] = tmp;}}
}· 时间复杂度:
最好情况下O(n),即数组有序的情况
最坏情况下O(n^2),即数组逆序的情况
· 空间复杂度:O(1)
· 稳定性: 稳定的排序算法
希尔排序
public class MySort {public static void shellSort(int[] array) {for (int gap = array.length / 2; gap > 1; gap /= 2) {shell(array, gap);}shell(array, 1);}private static void shell(int[] array, int gap) {for (int i = gap; i < array.length; i++) {int j = i - gap;int tmp = array[i];for (; j >= 0; j -= gap) {if (tmp < array[j]) {array[j + gap] = array[j];} else {break;}}array[j + gap] = tmp;}}
}· 时间复杂度:O(n^1.3)
· 空间复杂度:O(1)
· 稳定性: 不稳定的排序算法
选择排序
直接选择排序
public class MySort {public static void selectSort(int[] array) {for (int i = 0; i < array.length; i++) {int minIndex = i;for (int j = i + 1; j < array.length; j++) {if (array[minIndex] > array[j]) {minIndex = j;}}swap(array, minIndex, i);}}private static void swap(int[] array, int i, int j) {int tmp = array[i];array[i] = array[j];array[j] = tmp;}
}· 时间复杂度:O(n^2)
· 空间复杂度:O(1)
· 稳定性:不稳定的排序算法
堆排序
要排升序时,建立大根堆,排降序时,建立小根堆
public class MySort {public static void heapSort(int[] array) {//1、建立大根堆 时间复杂度:O(n)createHeap(array);//2、排序 时间复杂度:O(n*logn)int end = array.length - 1;while (end > 0) {swap(array, 0, end);shiftDown(array, 0, end);end--;}}private static void createHeap(int[] array) {for (int parent = (array.length-1-1) / 2; parent >= 0; parent--) {shiftDown(array, parent, array.length);}}private static void shiftDown(int[] array, int parent, int len) {int child = 2 * parent + 1;while (child < len) {if (child+1 < len && array[child] < array[child+1]) {child++;//他一定保存的是左右孩子的最大值的下标}if (array[child] > array[parent]) {swap(array, child, parent);parent = child;child = 2*parent + 1;} else {break;}}}private static void swap(int[] array, int i, int j) {int tmp = array[i];array[i] = array[j];array[j] = tmp;}
}· 时间复杂度:O(n*logn) 和数据是否有序无关
· 空间复杂度:O(1)
· 稳定性:不稳定的排序算法
交换排序
冒泡排序
public class MySort {public static void bubbleSort(int[] array) {for (int i = 0; i < array.length; i++) {boolean flag = false;for (int j = 0; j < array.length - i - 1; j++) {if (array[j + 1] < array[j]) {swap(array, j + 1, j);flag = true;}}if (flag == false) {return;}}}private static void swap(int[] array, int i, int j) {int tmp = array[i];array[i] = array[j];array[j] = tmp;}
}· 时间复杂度:O(n^2),优化后的冒泡排序时间复杂度最好可以到O(n)
· 空间复杂度:O(1)
· 稳定性:稳定的排序算法
快速排序
· 时间复杂度:
最好情况下:O(n*logn),待排序列尽量均匀的分割
最坏情况下:O(n^2),待排序列正序或逆序
· 空间复杂度:
最好情况下:O(logn)
最坏情况下:O(n)
· 稳定性:不稳定的排序算法
递归实现
public class MySort {public static void quickSort(int[] array) {quick(array, 0, array.length - 1);}private static void quick(int[] array, int start, int end) {if (start >= end) {return;}int pivot = partition(array, start, end);quick(array, start, pivot - 1);quick(array, pivot + 1, end);}private static int partition(int[] array, int left, int right) {int tmp = array[left];while (left < right) {while (left < right && array[right] >= tmp) {right--;}array[left] = array[right];while (left < right && array[left] <= tmp) {left++;}array[right] = array[left];}array[left] = tmp;return left;}
}优化版本
对于快速排序的优化,利用三数取中法选取key值,当递归到小的区间时,采用直接插入排序
public class MyQuickSort {private static final int INSERT_SIZE = 100;private static void quickSort(int[] array) {quick(array, 0, array.length - 1);}private static void quick(int[] array, int start, int end) {if (start >= end) {return;}if (end - start + 1 <= INSERT_SIZE) {insertSort(array, start, end);return;}int index = threeMid(array, start, end);swap(array, start, index);int pivot = partition(array, start, end);quick(array, start, pivot - 1);quick(array, pivot + 1, end);}/*** 针对快排的优化:key值根据三数取中法获得*/private static int threeMid(int[] array, int left, int right) {int mid = (left + right) >>> 1;if (array[left] > array[right]) {if (array[mid] > array[left]) {return left;} else if (array[mid] < array[right]) {return right;} else {return mid;}} else {if (array[mid] > array[right]) {return right;} else if (array[mid] < array[left]) {return left;} else {return mid;}}}/*** 针对快排的优化:当递归到小的区间时,快排转为插入排序*/private static void insertSort(int[] array, int start, int end) {for (int i = start + 1; i < end + 1; i++) {int j = i - 1;int tmp = array[i];for (; j >= start; j--) {if (tmp < array[j]) {array[j + 1] = array[j];} else {break;}}array[j + 1] = tmp;}}private static int partition(int[] array, int left, int right) {int tmp = array[left];while (left < right) {while (left < right && array[right] > tmp) {right--;}array[left] = array[right];while (left < right && array[left] < tmp) {left++;}array[right] = array[left];}array[left] = tmp;return left;}private static void swap(int[] array, int i, int j) {int tmp = array[i];array[i] = array[j];array[j] = tmp;}
}
归并排序
public class MySort {public static void mergeSort(int[] array) {mergeSortFunction(array, 0, array.length - 1);}private static void mergeSortFunction(int[] array, int low, int high) {if (low >= high) {return;}int mid = (low + high) >>> 1;mergeSortFunction(array, low, mid);mergeSortFunction(array, mid + 1, high);merge(array, low, high, mid);}private static void merge(int[] array, int low, int high, int mid) {int[] tmp = new int[high - low + 1];int k = 0;int start1 = low;int end1 = mid;int start2 = mid + 1;int end2 = high;while (start1 <= end1 && start2 <= end2) {if (array[start1] < array[start2]) {tmp[k++] = array[start1++];} else {tmp[k++] = array[start2++];}}while (start1 <= end1) {tmp[k++] = array[start1++];}while (start2 <= end2) {tmp[k++] = array[start2++];}for (int i = 0; i < k; i++) {array[i + low] = tmp[i];}}· 时间复杂度:O(n*logn),不论有序或无序都是O(n*logn)
· 空间复杂度:O(n)
· 稳定性: 稳定的排序算法
相关文章:
)
数据结构~七大排序算法(Java实现)
目录 插入排序 直接插入排序 希尔排序 选择排序 直接选择排序 堆排序 交换排序 冒泡排序 快速排序 递归实现 优化版本 归并排序 插入排序 直接插入排序 public class MySort {public static void insertSort(int[] array) {for (int i 1; i < array.length;…...
python练习
项目场景一: 假设你正在爬楼梯。需要 n 阶你才能到达楼顶。 每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢? 问题描述 假设你正在爬楼梯。需要 n 阶你才能到达楼顶。 每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶…...

RPC-thrift实践
参考:https://www.cnblogs.com/52fhy/p/11146047.html 参考:https://juejin.cn/post/7138032523648598030 实践 安装thrift brew install thriftthrift -version 编写thrift文件 新建文件夹thrift新建文件 结构体文件 Struct.thrift 服务文件 Service.…...
Maven:工程的拆分与聚合
Maven 拆分与聚合创建父工程创建子模块pom.xml配置示例拆分与聚合 在 Maven 中, 拆分是将一个完整的项目分成一个个独立的小模块,聚合是将各个模块进一步组合,形成一个完整的项目。接下来简单示例拆分与聚合的过程。 创建父工程 父工程,一个pom工程,目录结构简单,只需有…...
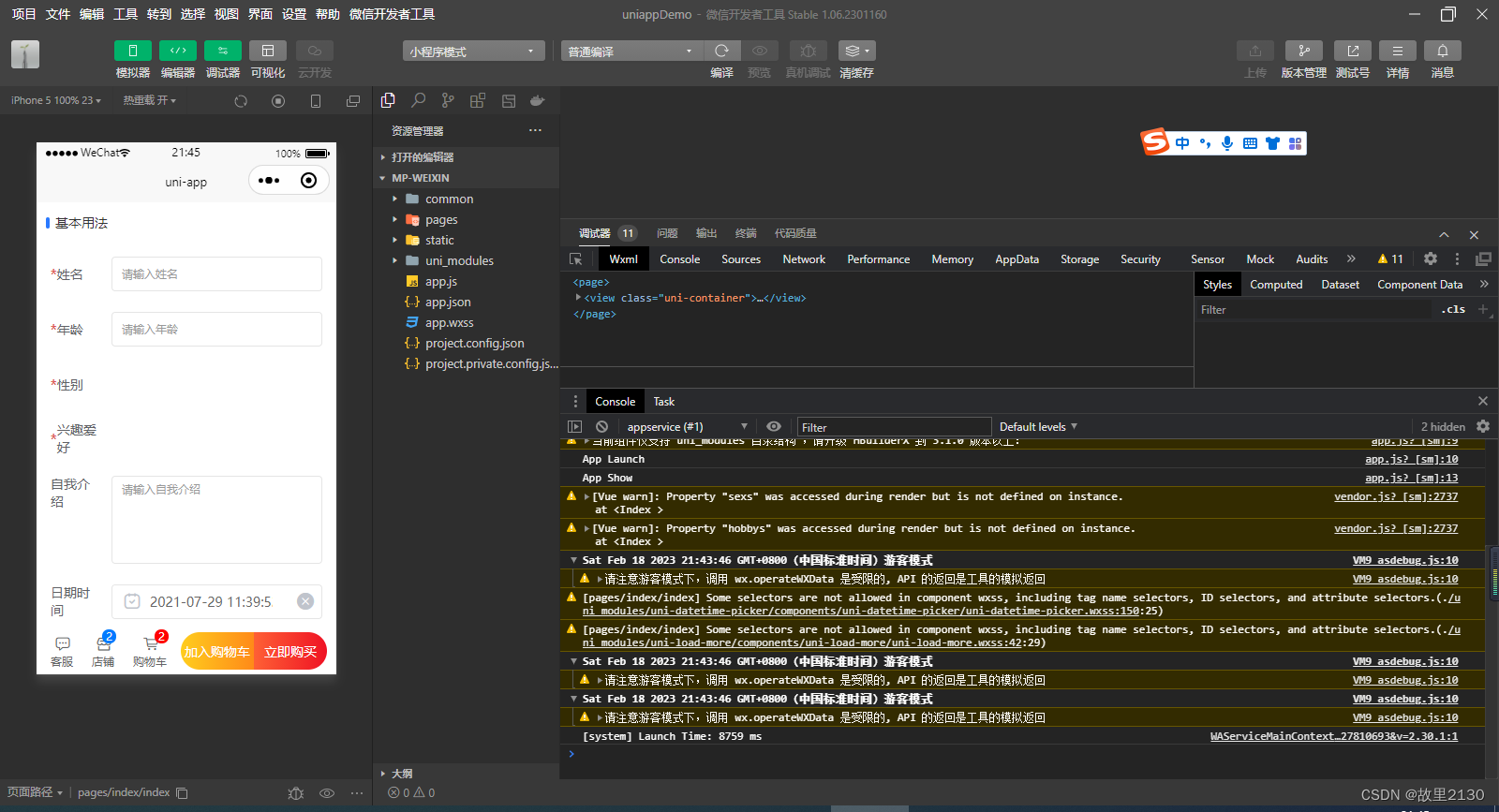
使用uniapp创建小程序和H5界面
uniapp的介绍可以看官网,接下来我们使用uniapp创建小程序和H5界面,其他小程序也是可以的,只演示创建这2个,其实都是一套代码,只是生成的方式不一样而已。 uni-app官网 1.打开HBuilder X 选择如图所示,下…...

密度峰值聚类算法(DPC)
密度峰值聚类算法目录DPC算法1.1 DPC算法的两个假设1.2 DPC算法的两个重要概念1.3 DPC算法的执行步骤1.4 DPC算法的优缺点matlab代码密度计算函数计算delta寻找聚类中心点聚类算法目录 DPC算法 1.1 DPC算法的两个假设 1)类簇中心被类簇中其他密度较低的数据点包围…...
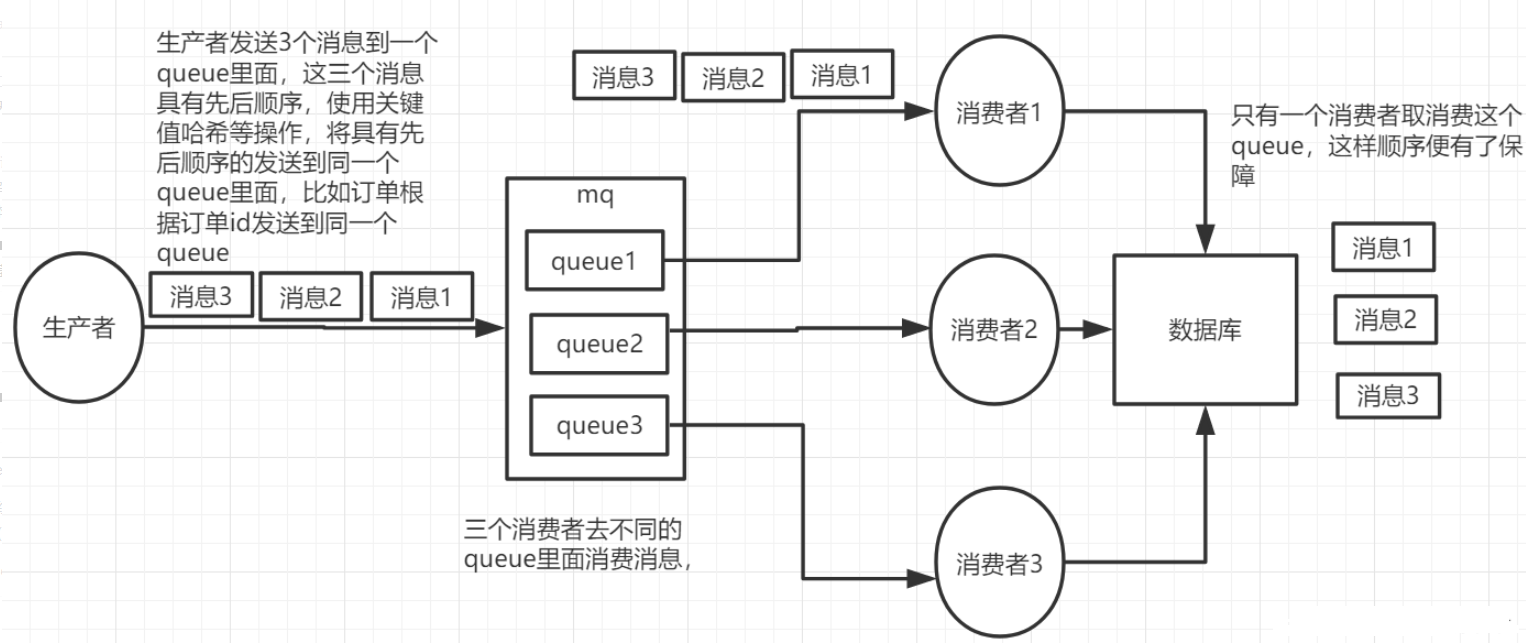
RabbitMQ相关问题
文章目录避免重复消费(保证消息幂等性)消息积压上线更多的消费者,进行正常消费惰性队列消息缓存延时队列RabbitMQ如何保证消息的有序性?RabbitMQ消息的可靠性、延时队列如何实现数据库与缓存数据一致?开启消费者多线程消费避免重复消费(保证消…...

操作系统 三(存储管理)
一、 存储系统的“金字塔”层次结构设计原理:cpu自身运算速度很快。内存、外存的访问速度受到限制各层次存储器的特点:1)主存储器(主存/内存/可执行存储器)保存进程运行时的程序和数据,内存的访问速度远低于…...

day34 贪心算法 | 860、柠檬水找零 406、根据身高重建队列 452、用最少数量的箭引爆气球
题目 860、柠檬水找零 在柠檬水摊上,每一杯柠檬水的售价为 5 美元。 顾客排队购买你的产品,(按账单 bills 支付的顺序)一次购买一杯。 每位顾客只买一杯柠檬水,然后向你付 5 美元、10 美元或 20 美元。你必须给每个…...

使用canvas给上传的整张图片添加平铺的水印
写在开头 哈喽,各位倔友们又见面了,本章我们继续来分享一个实用小技巧,给图片加水印功能,水印功能的目的是为了保护网站或作者版权,防止内容被别人利用或白嫖。 但是网络中,是没有绝对安全的,…...
[安装之4] 联想ThinkPad 加装固态硬盘教程
方案:保留原有的机械硬盘,再加装一个固态硬盘作为系统盘。由于X250没有光驱,这样就无法使用第二个2.5寸的硬盘。还好,X250留有一个M.2接口,这样,就可以使用NGFF M.2接口的固态硬盘。不过,这种接…...
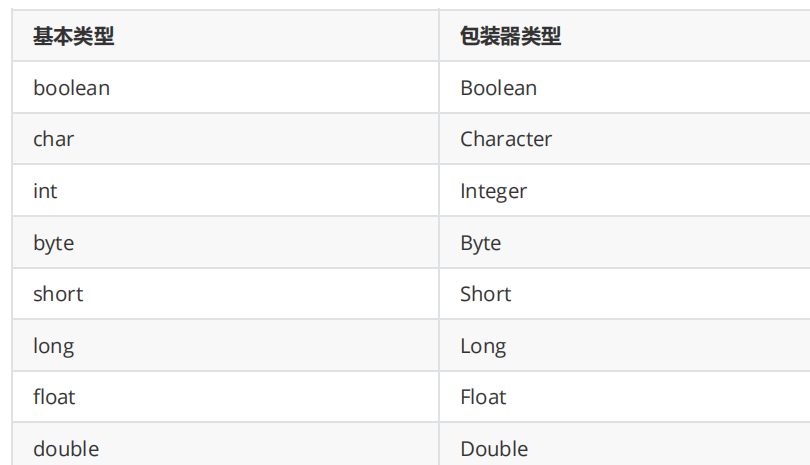
Java数据类型、基本与引用数据类型区别、装箱与拆箱、a=a+b与a+=b区别
文章目录1.Java有哪些数据类型2.Java中引用数据类型有哪些,它们与基本数据类型有什么区别?3.Java中的自动装箱与拆箱4.为什么要有包装类型?5.aab与ab有什么区别吗?1.Java有哪些数据类型 8种基本数据类型: 6种数字类型(4个整数型…...
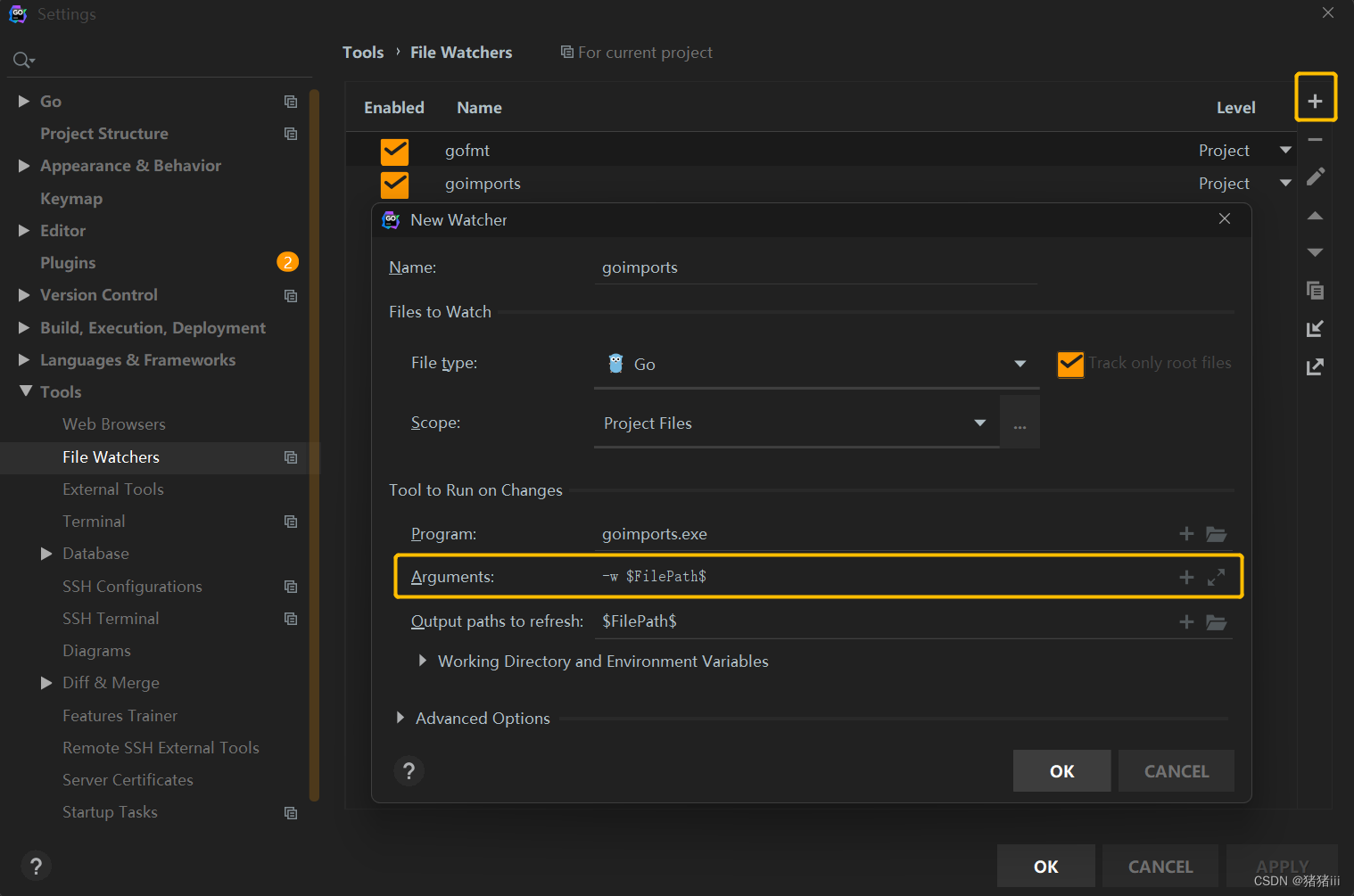
GoLang设置gofmt和goimports自动格式化
目录 设置gofmt gofmt介绍 配置gofmt 设置goimports goimports介绍 配置goimports 设置gofmt gofmt介绍 Go语言的开发团队制定了统一的官方代码风格,并且推出了 gofmt 工具(gofmt 或 go fmt)来帮助开发者格式化他们的代码到统一的风格…...

【k8s】如何搭建搭建k8s服务器集群(Kubernetes)
搭建k8s服务器集群 服务器搭建环境随手记 文章目录搭建k8s服务器集群前言:一、前期准备(所有节点)1.1所有节点,关闭防火墙规则,关闭selinux,关闭swap交换,打通所有服务器网络,进行p…...
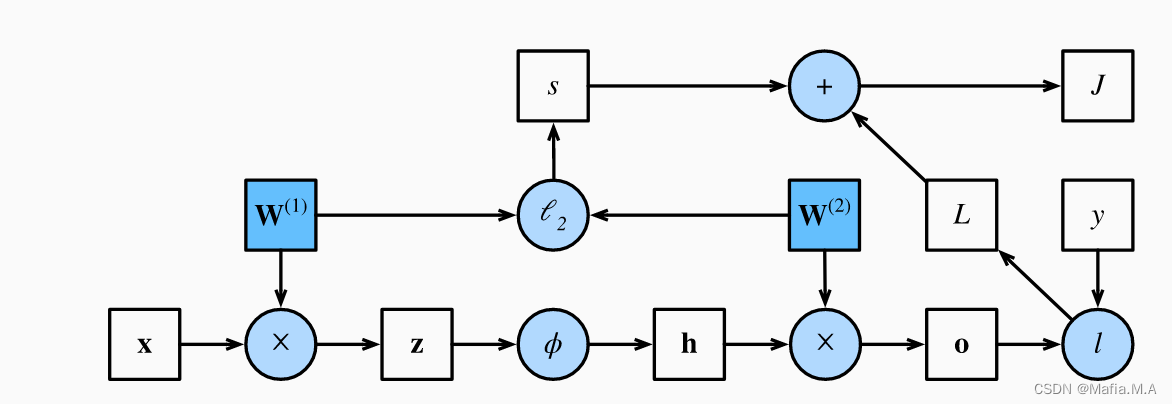
DIDL4_前向传播与反向传播(模型参数的更新)
前向传播与反向传播前向传播与反向传播的作用前向传播及公式前向传播范例反向传播及公式反向传播范例小结前向传播计算图前向传播与反向传播的作用 在训练神经网络时,前向传播和反向传播相互依赖。 对于前向传播,我们沿着依赖的方向遍历计算图并计算其路…...

链表学习之链表划分
链表解题技巧 额外的数据结构(哈希表);快慢指针;虚拟头节点; 链表划分 将单向链表值划分为左边小、中间相等、右边大的形式。中间值为pivot划分值。 要求:调整之后节点的相对次序不变,时间复…...

(考研湖科大教书匠计算机网络)第五章传输层-第一、二节:传输层概述及端口号、复用分用等概念
获取pdf:密码7281专栏目录首页:【专栏必读】考研湖科大教书匠计算机网络笔记导航 文章目录一:传输层概述(1)概述(2)从计算机网络体系结构角度看传输层(3)传输层意义二&am…...

C#:Krypton控件使用方法详解(第七讲) ——kryptonHeader
今天介绍的Krypton控件中的kryptonHeader,下面开始介绍这个控件的属性:控件的样子如上图所示,从上面控件外观来看,这个控件有三部分组成。第一部分是前面的图片,第二部分是kryptonHeader1文本,第三部分是控…...

5年软件测试工程师分享的自动化测试经验,一定要看
今天给大家分享一个华为的软件测试工程师分享的关于自动化测试的经验及干货。真的后悔太晚找他要了, 纯干货。一定要看完! 1.什么是自动化测试? 用程序测试程序,用代码取代思考,用脚本运行取代手工测试。自动化测试涵…...

什么是猜疑心理?小猫测试网科普小作文
什么是猜疑心理?猜疑心理是说一个人心中想法偏离了客观事实,牵强附会,往往是指不好的一面,对别人的一言一行都充满了不良的解读,认为这些对自己都有针对性,目的性,对自己都是不利的。猜疑心理重…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

Linux部署私有文件管理系统MinIO
最近需要用到一个文件管理服务,但是又不想花钱,所以就想着自己搭建一个,刚好我们用的一个开源框架已经集成了MinIO,所以就选了这个 我这边对文件服务性能要求不是太高,单机版就可以 安装非常简单,几个命令就…...

深度剖析 DeepSeek 开源模型部署与应用:策略、权衡与未来走向
在人工智能技术呈指数级发展的当下,大模型已然成为推动各行业变革的核心驱动力。DeepSeek 开源模型以其卓越的性能和灵活的开源特性,吸引了众多企业与开发者的目光。如何高效且合理地部署与运用 DeepSeek 模型,成为释放其巨大潜力的关键所在&…...

WEB3全栈开发——面试专业技能点P7前端与链上集成
一、Next.js技术栈 ✅ 概念介绍 Next.js 是一个基于 React 的 服务端渲染(SSR)与静态网站生成(SSG) 框架,由 Vercel 开发。它简化了构建生产级 React 应用的过程,并内置了很多特性: ✅ 文件系…...

归并排序:分治思想的高效排序
目录 基本原理 流程图解 实现方法 递归实现 非递归实现 演示过程 时间复杂度 基本原理 归并排序(Merge Sort)是一种基于分治思想的排序算法,由约翰冯诺伊曼在1945年提出。其核心思想包括: 分割(Divide):将待排序数组递归地分成两个子…...
