算法导论【在线算法】—The Ski-Rental Problem、The Lost Cow Problem、The Secretary Problem
算法导论【在线算法】
- The Ski-Rental Problem
- 问题描述
- 在线算法
- 证明
- The Lost Cow Problem
- 问题描述
- 在线算法
- 类似问题—寻宝藏
- The Secretary Problem
- 问题描述
- 在线算法
- The Best Possible k
The Ski-Rental Problem
问题描述
- 假设你正在上滑雪课。每节课结束后,你决定(取决于你喜欢的程度、你的骨骼状况和天气)是继续滑雪还是完全停止滑雪。
- 你可以选择以1美元一次的价格租用滑雪板,也可以以B美元的价格购买滑雪板。
- 你是买还是租?
- 如果你事先知道你一生中会滑雪多少次,那么选择租还是买就很简单了。
- 如果你要滑雪超过BBB次,那就在开始前购买,否则就一直租。该算法的代价为min(T,B)min(T,B)min(T,B)。
- 这种对未来了如指掌的策略被称为离线策略。
在线算法
- 实际上,你不知道你会滑雪多少次。你该怎么办?
- 在线策略是:取一个数字k,这样在租用k−1次后,您将购买滑雪板(就在第k次滑雪之前)。
- 如果我们取k=Bk=Bk=B,那么可以保证我们支付不会超过离线策略成本两倍的费用
- 例如:假设B=7美元,那么,在6次租金之后,你就买了。总付款:6+7=13$
证明
最坏情况下,k=Bk=Bk=B,我们选择在滑雪次数T=k−1T=k-1T=k−1次后再也不滑雪,那么在线算法的总费用为B−1+B=2B−1B-1+B=2B-1B−1+B=2B−1,而离线算法取得的最优解为min(T,B)=Bmin(T,B)=Bmin(T,B)=B,此时竞争比为2B−1B=2−1B\cfrac{2B-1}{B}=2-\cfrac{1}{B}B2B−1=2−B1,则我们说这个策略是(2−1B)(2-\cfrac{1}{B})(2−B1)竞争的

The Lost Cow Problem
问题描述
- Old McDonald失去了他最喜欢的奶牛。最后一次看到它朝着通向两条无限道路的路口行进。没有一位目击者能说出奶牛是选择了左边还是右边的路线。

在线算法
- 在线算法是9-competitive的,换句话说:在找到奶牛之前可能经过的距离最多是最佳离线算法(知道奶牛在哪里)距离的9倍
- 最坏的情况是,他发现奶牛的距离比他上次在这一侧搜索的距离稍远
- 因此,OPT=2j+εOPT=2j+εOPT=2j+ε,其中j=j=j=迭代次数,εεε是某个小距离。然后

- 伪代码如下:

类似问题—寻宝藏


mmm条路编号为1,2,3...m1,2,3...m1,2,3...m,从第一条路开始寻找,初始寻找距离为d=1d=1d=1,如果在这个距离内找到了宝藏则结束寻找,没找到则寻找距离翻倍,切换至寻找下一条路径,路径编号对mmm取模,保证每次寻找的路径都是合法的,直到找到宝藏。
Treasure(m)
d = 1;current side = 1
while true doWalk distance d on current sideif find treasure thenexitelsed = 2dcurrent side = (current side+1)%mreturn to starting point
该算法的竞争比为O(m)O(m)O(m)
证明:
最坏的情况是,发现宝藏的距离比上次在这条路上搜索的距离稍远一点点,因此,最优解为OPT:2j+εOPT:2^j +εOPT:2j+ε,其中jjj=迭代次数,εεε是某个小距离。则:
CostOPT=2j+ε>2jCostON=m(1+2+4+...+2j+1)+2j+ε=m⋅2j+2+2j+ε=(4m+1)⋅2j+ε<(4m+1)⋅CostOPT\begin{aligned} Cost OPT &= 2^j +ε>2^j\\ \ \ \ \ \ \ Cost ON&= m(1+2+4+...+2^{j+1})+2^j +ε\\ &= m · 2^{j+2} +2^j +ε = (4m+1)· 2^j +ε < (4m+1) · Cost OPT \end{aligned} CostOPT CostON=2j+ε>2j=m(1+2+4+...+2j+1)+2j+ε=m⋅2j+2+2j+ε=(4m+1)⋅2j+ε<(4m+1)⋅CostOPT
所以竞争比为O(4m+1)=O(m)O(4m+1)=O(m)O(4m+1)=O(m)
The Secretary Problem
问题描述
- 我们有
n位候选人(可能是求职者或可能的婚姻伴侣)。 - 我们的目标是选择最好的候选人。
- 假设候选人可以从最好到最坏完全排序,没有任何联系。
- 候选人以随机顺序依次到达。
- 我们只能在候选人到达时确定他们的相对排名。
- 我们不能观察绝对等级。
- 每次面试后,我们必须立即接受或拒绝申请人。
- 候选人一旦被拒绝,就不能被召回。
- 一旦候选人被录取,我们就停止面试。
在线算法
- 已知候选人数
n - 在线策略在遇到第
i位候选人后,我们能够给出分数score(i)。 - 选择一个正整数
k<n,面试并拒绝前k位候选人。 - 继续面试剩下的
n-k位,并接受第一位得分高于前k位候选人的候选人。 - 如果最高分在第一批面试的
k人里,那么我们必须接受第n位即最后一位申请人 - 伪代码:

The Best Possible k
结论:如果我们在k=nek=\cfrac{n}{e}k=en的情况下实施我们的策略,我们将以至少1e\cfrac{1}{e}e1的概率成功雇佣我们最合格的申请人
相关文章:

算法导论【在线算法】—The Ski-Rental Problem、The Lost Cow Problem、The Secretary Problem
算法导论【在线算法】The Ski-Rental Problem问题描述在线算法证明The Lost Cow Problem问题描述在线算法类似问题—寻宝藏The Secretary Problem问题描述在线算法The Best Possible kThe Ski-Rental Problem 问题描述 假设你正在上滑雪课。每节课结束后,你决定&a…...

linux 下怎样给pdf 文件加书签
linux 下怎样给pdf 文件加书签 对于没有书签的pdf文件,怎样给pdf加标签呢? 以方便阅读. 以前总是要借助windows下pdf 工具, 叫什么来者? 忘了 记得是编辑一个用tab表示目录级别的文本文件, 有一种直观的感觉,大目录下嵌套着小目录 ..., 然后导入到文件中 linux 下有没有这种…...
[软件工程导论(第六版)]第2章 可行性研究(课后习题详解)
文章目录1. 在软件开发的早期阶段为什么要进行可行性研究?应该从哪些方面研究目标系统的可行性?2. 为方便储户,某银行拟开发计算机储蓄系统。储户填写的存款单或取款单由业务员输入系统,如果是存款,系统记录存款人姓名…...
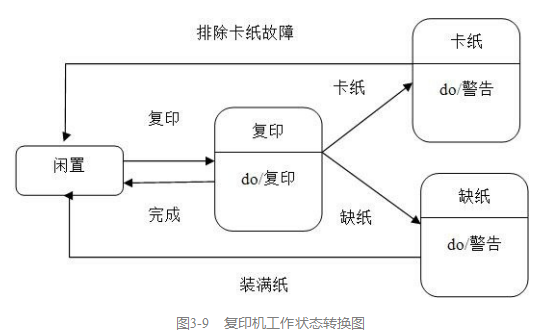
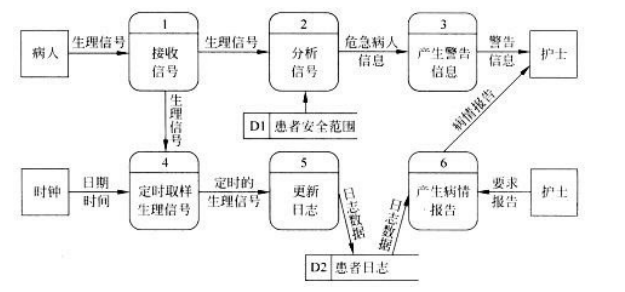
[软件工程导论(第六版)]第3章 需求分析(课后习题详解)
文章目录1. 为什么要进行需求分析?通常对软件系统有哪些需求?2. 怎样与用户有效地沟通以获取用户的真实需求?3. 银行计算机储蓄系统的工作过程大致如下:储户填写的存款单或取款单由业务员输入系统,如果是存款则系统记录…...

基于分布鲁棒联合机会约束的能源和储备调度(Matlab代码实现)
👨🎓个人主页:研学社的博客 💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜…...

ETL和数据建模
一、什么是ETL ETL是数据抽取(Extract)、转换(Transform)、加载(Load )的简写,它是将OLTP系统中的数据经过抽取,并将不同数据源的数据进行转换、整合,得出一致性的数据&…...

ccc-pytorch-回归问题(1)
文章目录1.简单回归实战:2.手写数据识别1.简单回归实战: 用 线性回归拟合二维平面中的100个点 公式:ywxbywxbywxb 损失函数:∑(yreally−y)2\sum(y_{really}-y)^2∑(yreally−y)2 迭代方法:梯度下降法,…...

【JAVA八股文】框架相关
框架相关1. Spring refresh 流程2. Spring bean 生命周期3. Spring bean 循环依赖解决 set 循环依赖的原理4. Spring 事务失效5. Spring MVC 执行流程6. Spring 注解7. SpringBoot 自动配置原理8. Spring 中的设计模式1. Spring refresh 流程 Spring refresh 概述 refresh 是…...
二叉树的相关列题!!
对于二叉树,很难,很难!笔者也是感觉很难!虽然能听懂课程,但是,对于大部分的练习题并不能做出来!所以感觉很尴尬!!因此,笔者经过先前的那篇博客,已…...

Java设计模式 - 原型模式
简介 原型模式(Prototype Pattern)是用于创建重复的对象,同时又能保证性能。这种类型的设计模式属于创建型模式,它提供了一种创建对象的最佳方式。 这种模式是实现了一个原型接口,该接口用于创建当前对象的克隆。当直…...

深度学习中的 “Hello World“
Here’s an interesting fact—Each month, there are 186.000 Google searches for the keyword “deep learning.” 大家好✨,这里是bio🦖。每月有超18万的人使用谷歌搜索深度学习这一关键词,是什么让人们对深度学习如此感兴趣?接下来请跟随我来揭开深度学习的神秘面纱。…...

购买WMS系统前,有搞清楚与ERP仓库模块的区别吗
经常有朋友在后台询问我们关于WMS系统的问题,他们自己也有ERP系统,但是总觉得好像还差了点什么,不知道是什么。今天,我想通过本文,来向您简要地阐述ERP与WMS系统在仓储管理上的不同之处。 ERP仓库是以财务为导向的&…...

一文吃透 Spring 中的IOC和DI
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...
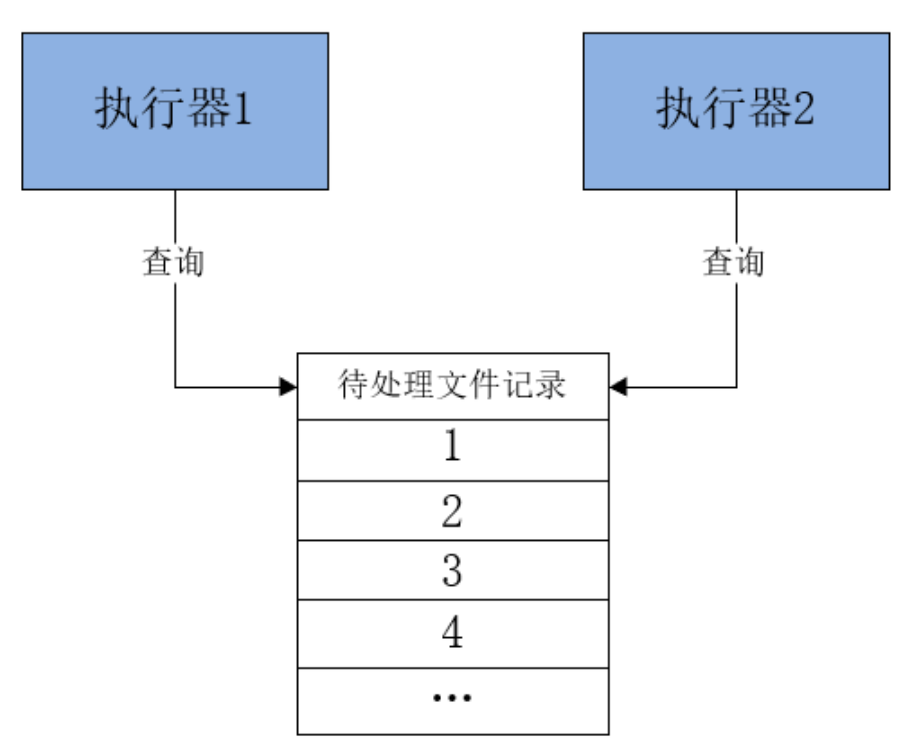
分布式任务处理:XXL-JOB分布式任务调度框架
文章目录1.业务场景与任务调度2.任务调度的基本实现2.1 多线程方式实现2.2 Timer方式实现2.3 ScheduledExecutor方式实现2.4 第三方Quartz方式实现3.分布式任务调度4.XXL-JOB介绍5.搭建XXL-JOB —— 调度中心5.1 下载与查看XXL-JOB5.2 创建数据库表5.3 修改默认的配置信息5.4 启…...

【源码解析】Ribbon和Feign实现不同服务不同的配置
Ribbon服务实现不同服务,不同配置是通过RibbonClient和RibbonClients两个注解来实现的。RibbonClient注册的某个Client配置类。RibbonClients注册的全局默认配置类。 Feign实现不同服务,不同配置,是根据FeignClient来获取自定义的配置。 示…...
【webpack5】一些常见优化配置及原理介绍(二)
这里写目录标题介绍sourcemap定位报错热模块替换(或热替换,HMR)oneOf精准解析指定或排除编译开启缓存多进程打包移除未引用代码配置babel,减小代码体积代码分割(Code Split)介绍预获取/预加载(prefetch/pre…...

力扣sql简单篇练习(十九)
力扣sql简单篇练习(十九) 1 查询结果的质量和占比 1.1 题目内容 1.1.1 基本题目信息 1.1.2 示例输入输出 1.2 示例sql语句 # 用count是不会统计为null的数据的 SELECT query_name,ROUND(AVG(rating/position),2) quality,ROUND(count(IF(rating<3,rating,null))/count(r…...

线段树c++
前言 在谈论到种种算法知识与数据结构的时候,线段树无疑总是与“简单”和“平常”联系起来的。而这些特征意味着,线段树作为一种常用的数据结构,有常用性,基础性和易用性等诸多特点。因此,今天我来讲一讲关于线段树的话题。 定义 首先,线段树是一棵“树”,而且是一棵…...
HTML+CSS+JavaScript学习笔记~ 从入门到精通!
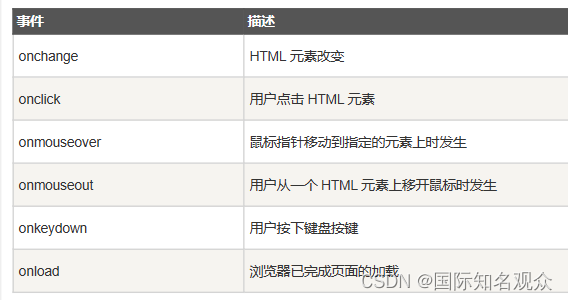
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录前言一、HTML1. 什么是HTML?一个完整的页面:<!DOCTYPE> 声明中文编码2.HTML基础①标签头部元素标题段落注释水平线文本格式化②属性3.H…...
LeetCode 430. 扁平化多级双向链表
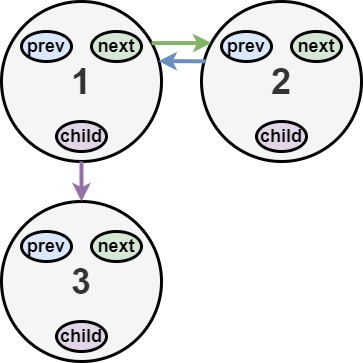
原题链接 难度:middle\color{orange}{middle}middle 题目描述 你会得到一个双链表,其中包含的节点有一个下一个指针、一个前一个指针和一个额外的 子指针 。这个子指针可能指向一个单独的双向链表,也包含这些特殊的节点。这些子列表可以有一…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

在树莓派上添加音频输入设备的几种方法
在树莓派上添加音频输入设备可以通过以下步骤完成,具体方法取决于设备类型(如USB麦克风、3.5mm接口麦克风或HDMI音频输入)。以下是详细指南: 1. 连接音频输入设备 USB麦克风/声卡:直接插入树莓派的USB接口。3.5mm麦克…...

Axure 下拉框联动
实现选省、选完省之后选对应省份下的市区...
