算法导论【摊还分析】—聚合分析、核算法、势能法
算法导论【摊还分析】—聚合分析、核算法、势能法
- 聚合分析
- 核算法
- 势能法
假定我们对一个数据结构执行一个由 n 个操作组成的操作序列,当 i 严格为 2 的幂时,第 i 个操作的代价为 i,否则代价为 1
聚合分析
总共有n个操作,1,2,4.....,2⌊lgn⌋1,2,4.....,2^{⌊\lg n⌋}1,2,4.....,2⌊lgn⌋,其中有至多k=⌈lgn⌉k=⌈\lg n⌉k=⌈lgn⌉个操作序号为2的幂,则
S=∑k=0⌊lgn⌋2k+(n−⌈lgn⌉)∗1=1∗(1−2⌊lgn⌋+1)1−2+n−⌈lgn⌉=2⌊lgn⌋+1−1+n−⌈lgn⌉=≤3n−⌈lgn⌉−1=O(n)\begin{aligned} S&=\sum_{k=0}^{⌊\lg n⌋}2^k+(n-⌈\lg n⌉)*1\\ &=\cfrac{1*(1-2^{⌊\lg n⌋+1})}{1-2}+n-⌈\lg n⌉\\ &=2^{⌊\lg n⌋+1}-1+n-⌈\lg n⌉\\ &=\le3n-⌈\lg n⌉-1\\ &=O(n) \end{aligned} S=k=0∑⌊lgn⌋2k+(n−⌈lgn⌉)∗1=1−21∗(1−2⌊lgn⌋+1)+n−⌈lgn⌉=2⌊lgn⌋+1−1+n−⌈lgn⌉=≤3n−⌈lgn⌉−1=O(n)
所以每个操作的摊还时间代价为O(n)n=O(1)\cfrac{O(n)}{n}=O(1)nO(n)=O(1)
核算法
设每个操作的代价都为333
第2k−1+1到第2k−12^{k-1}+1到第2^{k}-12k−1+1到第2k−1个操作为非2的幂,多付的代价为2∗(2k−1−1−1+1)=2k−22*(2^{k-1}-1-1+1)=2^k-22∗(2k−1−1−1+1)=2k−2在第2k2^k2k个次操作付的代价为333,则可以用于支付第2k2^k2k次操作的信用为2k−2+3=2k+1>2k2^k-2+3=2^k+1>2^k2k−2+3=2k+1>2k大于第2k2^k2k次操作应该付的代价,故每个操作的摊还代价为O(1)O(1)O(1)
势能法
设势函数为
Φ(D0)=0Φ(Di)=2(i−2lg⌊i⌋)\Phi (D_0) = 0\\ \Phi(D_i) = 2(i-2^{\lg⌊i⌋})\\ Φ(D0)=0Φ(Di)=2(i−2lg⌊i⌋)
- 当i为2的幂时,2⌊lgi⌋=i,⌊lg(i−1)⌋+1=⌊lgi⌋2^{⌊\lg i⌋}=i,⌊\lg (i-1)⌋+1=⌊\lg i⌋2⌊lgi⌋=i,⌊lg(i−1)⌋+1=⌊lgi⌋
c^i=ci+Φ(Di)−Φ(Di−1)=i+2(i−2⌊lgi⌋)−2(i−1−2⌊lgi−1⌋)=i+2i−2i+2−2⌊lgi⌋+1+2⌊lgi⌋+1=i−i−2⌊lgi⌋+2⌊lgi⌋+1+2=2\begin{aligned} \hat c_i&=c_i+\Phi(D_i)-\Phi(D_{i-1})\\ &=i+2(i-2^{⌊\lg i⌋})- 2(i-1-2^{⌊\lg i-1⌋})\\ &=i+2i-2i+2-2^{⌊\lg i⌋+1}+2^{⌊\lg i⌋+1}\\ &=i-i-2^{⌊\lg i⌋}+2^{⌊\lg i⌋+1}+2\\ &=2 \end{aligned} c^i=ci+Φ(Di)−Φ(Di−1)=i+2(i−2⌊lgi⌋)−2(i−1−2⌊lgi−1⌋)=i+2i−2i+2−2⌊lgi⌋+1+2⌊lgi⌋+1=i−i−2⌊lgi⌋+2⌊lgi⌋+1+2=2 - 当i不为2的幂时,2⌊lg(i−1)⌋=2⌊lgi⌋2^{⌊\lg (i-1)⌋}=2^{⌊\lg i⌋}2⌊lg(i−1)⌋=2⌊lgi⌋
c^i=ci+Φ(Di)−Φ(Di−1)=1+2(i−2⌊lgi⌋)−2(i−1−2⌊lgi−1⌋)=1+2i−2i+2−2(2⌊lgi⌋−2⌊lgi−1⌋)=1+2=3\begin{aligned} \hat c_i&=c_i+\Phi(D_i)-\Phi(D_{i-1})\\ &=1+2(i-2^{⌊\lg i⌋})- 2(i-1-2^{⌊\lg i-1⌋})\\ &=1+2i-2i+2-2(2^{⌊\lg i⌋}-2^{⌊\lg i-1⌋})\\ &=1+2\\ &=3 \end{aligned} c^i=ci+Φ(Di)−Φ(Di−1)=1+2(i−2⌊lgi⌋)−2(i−1−2⌊lgi−1⌋)=1+2i−2i+2−2(2⌊lgi⌋−2⌊lgi−1⌋)=1+2=3
故每个操作摊还复杂度为O(1)O(1)O(1)
相关文章:

算法导论【摊还分析】—聚合分析、核算法、势能法
算法导论【摊还分析】—聚合分析、核算法、势能法聚合分析核算法势能法假定我们对一个数据结构执行一个由 n 个操作组成的操作序列,当 i 严格为 2 的幂时,第 i 个操作的代价为 i,否则代价为 1 聚合分析 总共有n个操作,1,2,4.....…...
【LeetCode】剑指 Offer 08. 二叉树的下一个节点 p65 -- Java Version
题目链接:无题目链接,不知道为啥力扣上找不到这一题。 1. 题目介绍(08. 二叉树的下一个节点) 题目:给定一个二叉树和其中的一个节点,请找出中序遍历顺序的下一个节点并且返回。注意,树中的节点…...

Python 之 Pandas Series 数据结构
文章目录一、Series 结构二、数据结构 Series 创建1. 创建1.1 列表/数组作为数据源创建 Series1.2 字典作为数据源创建 Series1.3 通过标量创建2. 参数说明2.1 index 参数2.2 name 参数2.3 copy 参数三、Series 的索引/切片1. 下标索引2. 标签索引3. 切片四、Series 数据结构的…...
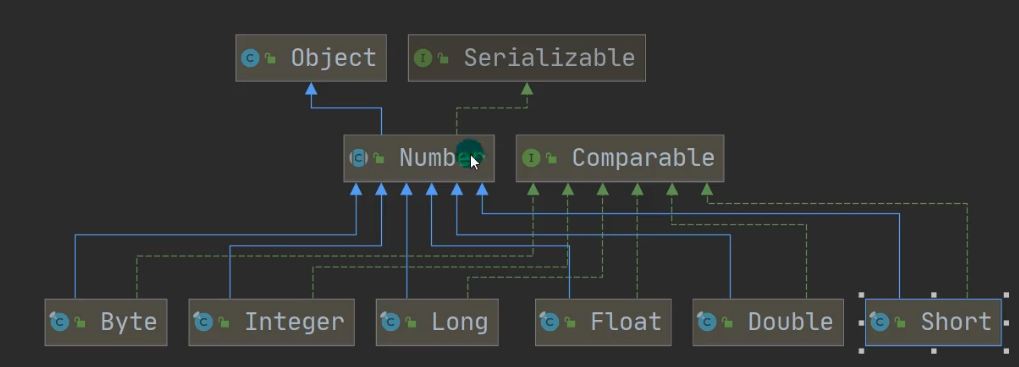
【java基础】Java常用类———包装类
包装类 wrapper 装箱与拆箱 装箱:基本类型->包装类; 拆箱: 包装类->基本类型 public class Integer01 {public static void main(String[] args) {//演示int <--> Integer 的装箱和拆箱//jdk5前是手动装箱和拆箱//手动装箱 in…...

linux shell 入门学习笔记3 shebang
shebang 计算机程序中,shebang指的是出现在文本文件的第一行前两个字符#! 在Unix系统中,程序会分析shebang后面的内容,作为解释器的指令,例如 以#!/bin/sh 开头的文件,程序在执行的时候会调用/bin/sh,也就…...
)
写作小课堂:简历模版【A4纸正反两面】(20230219)
文章目录 I 联系方式II 个人信息III 求职意向IV 工作经验2018年-11月-至今全城淘信息技术服务有限公司2017年07月-2018年-11月湖南微流网络科技有限公司2014年06月-2017年07月湖南高阳通联信息技术有限公司V 项目经验2018年11月-至今全城淘淘管家2017年10月-2018年11月ASO(机刷…...
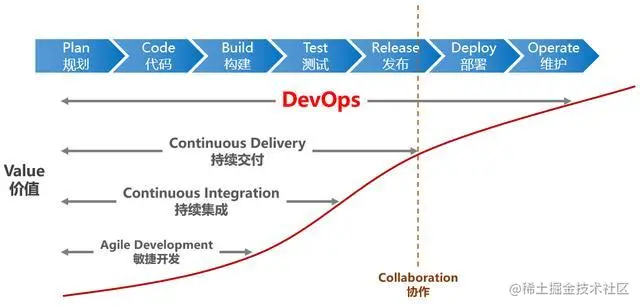
一文搞懂 DevOps
前言 DevOps作为一个热门的概念,近年来频频出现在各大技术社区和媒体的文章中,备受行业大咖的追捧,也吸引了很多吃瓜群众的围观。 那么,DevOps是什么呢? 有人说它是一种方法,也有人说它是一种工具&#…...

深入讲解Kubernetes架构-租约
分布式系统通常需要租约(Lease);租约提供了一种机制来锁定共享资源并协调集合成员之间的活动。 在 Kubernetes 中,租约概念表示为 coordination.k8s.io API 组中的 Lease 对象, 常用于类似节点心跳和组件级领导者选举等…...
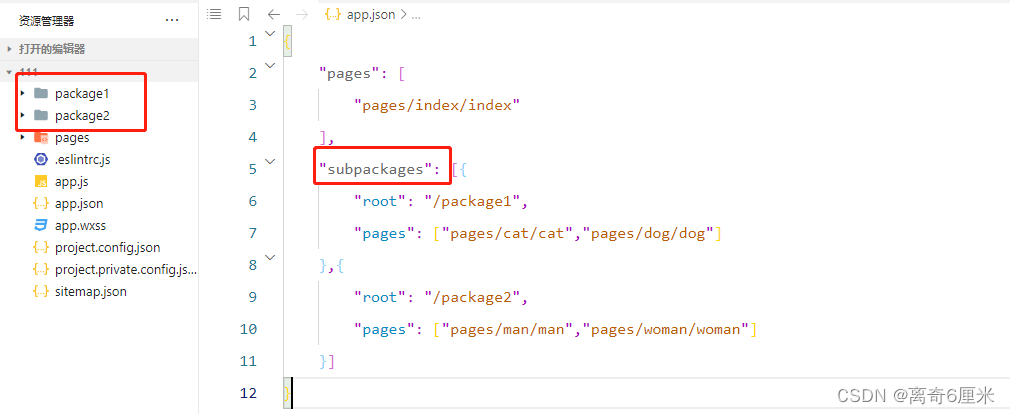
微信小程序学习第11天——Vant Weapp组件库、API Promise化、全局数据共享Mobx、分包
目录一、小程序对npm 的限制二、使用Vant Weapp组件库1、安装组件2、使用组件3、定制全局样式三、API Promise化1、下载miniprogram-api-promise2、引入3、使用四、全局数据共享五、分包1、分包概念2、使用分包3、独立分包4、分包预下载一、小程序对npm 的限制 在小程序中使用…...
Python3-基本数据类型
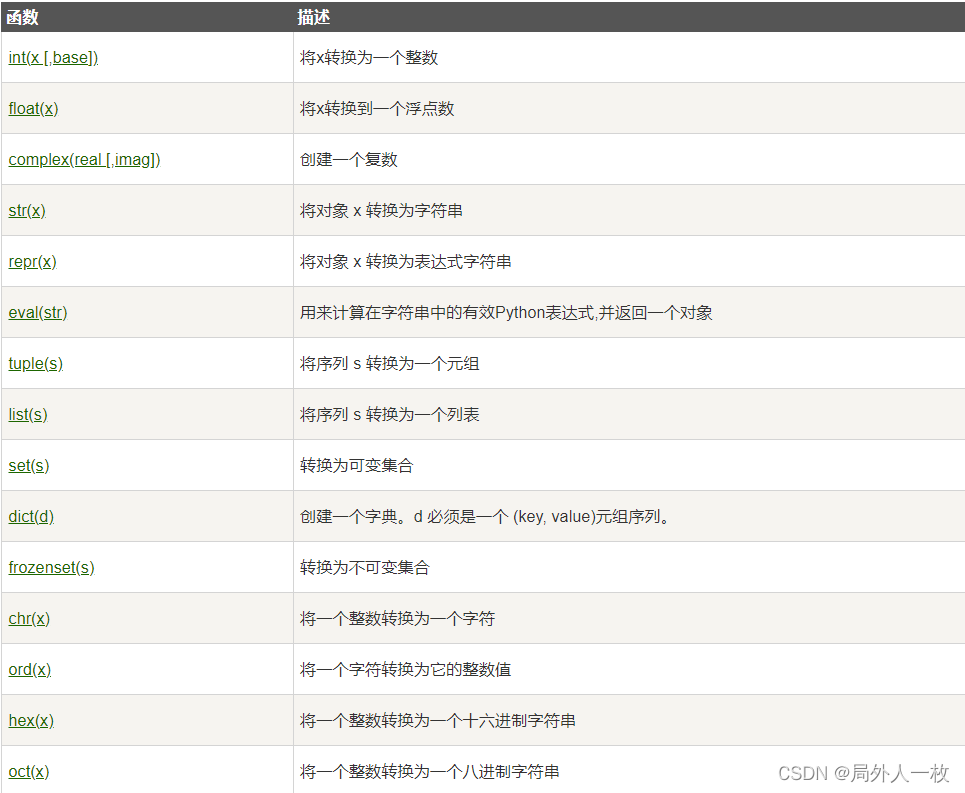
Python3 基本数据类型 Python 中的变量不需要声明。每个变量在使用前都必须赋值,变量赋值以后该变量才会被创建。 在 Python 中,变量就是变量,它没有类型,我们所说的"类型"是变量所指的内存中对象的类型。 等号&…...

RPA落地指南:什么是RPA
什么是RPA RPA在企业中起什么作用并扮演什么角色呢?想要充分了解RPA,我们需要知道RPA的相关概念、特点、功能以及能解决的问题。接下来对这些内容进行详细介绍。 1.1 RPA的3个核心概念 RPA的中文译名是“机器人流程自动化”,顾名思义&…...
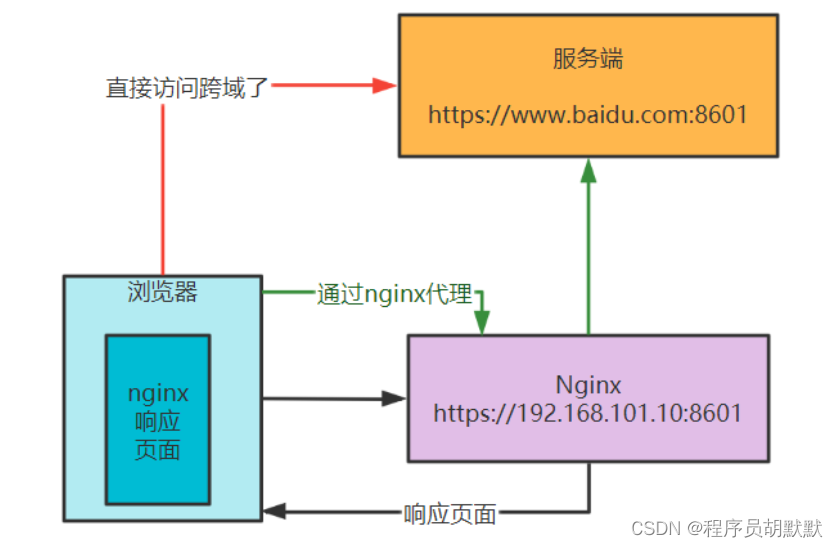
跨域问题的三种解决办法
我们平时对于前后端联调的项目,以下的错误是经常常见的,我们查看浏览器报错: Access to XMLHttpRequest at http://localhost:63110/system/dictionary/all fromorigin http://localhost:8601 has been blocked by CORS policy: No Access…...

c++提高篇——string容器
一、string基本概念 string是C风格的字符串,而string本质上是一个类。 与c语言不同,string是一个类,类内部封装了char*,管理这个字符串,是一个char型的容器。在根本上与c语言字符串是一致的。 在string类内部封装了很…...
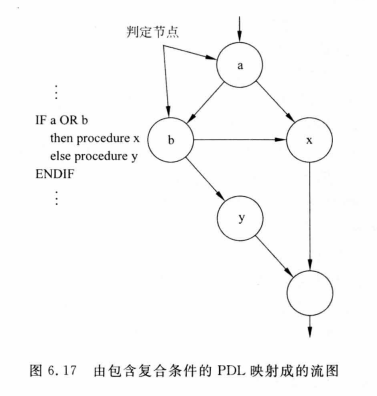
[软件工程导论(第六版)]第6章 详细设计(复习笔记)
文章目录6.1 结构程序设计6.2 人机界面设计6.3 过程设计的工具6.3.1 程序流程图(程序框图)6.3.2 盒图(N-S图)6.3.3 PAD图(问题分析图)6.3.4 判定表6.3.5 判断树6.3.6 过程设计语言6.4 面向数据结构的设计方…...
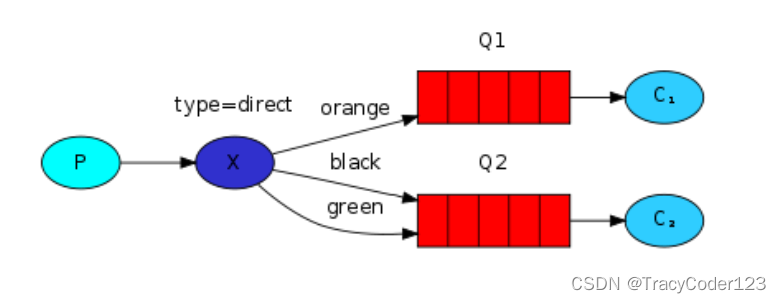
RabbitMQ核心内容:实战教程(java)
文章目录一、安装二、入门1.分类2.核心概念3.工作原理4.六大模式三、模式一:"Hello World!"1.依赖2.生产者代码3.消费者代码四、模式二:Work Queues1.工作原理2.工具类代码:连接工厂3.消费者代码4.生产者代码5.分发策略不公平分发预…...
RK356x U-Boot研究所(命令篇)3.7 pci与nvme命令的用法
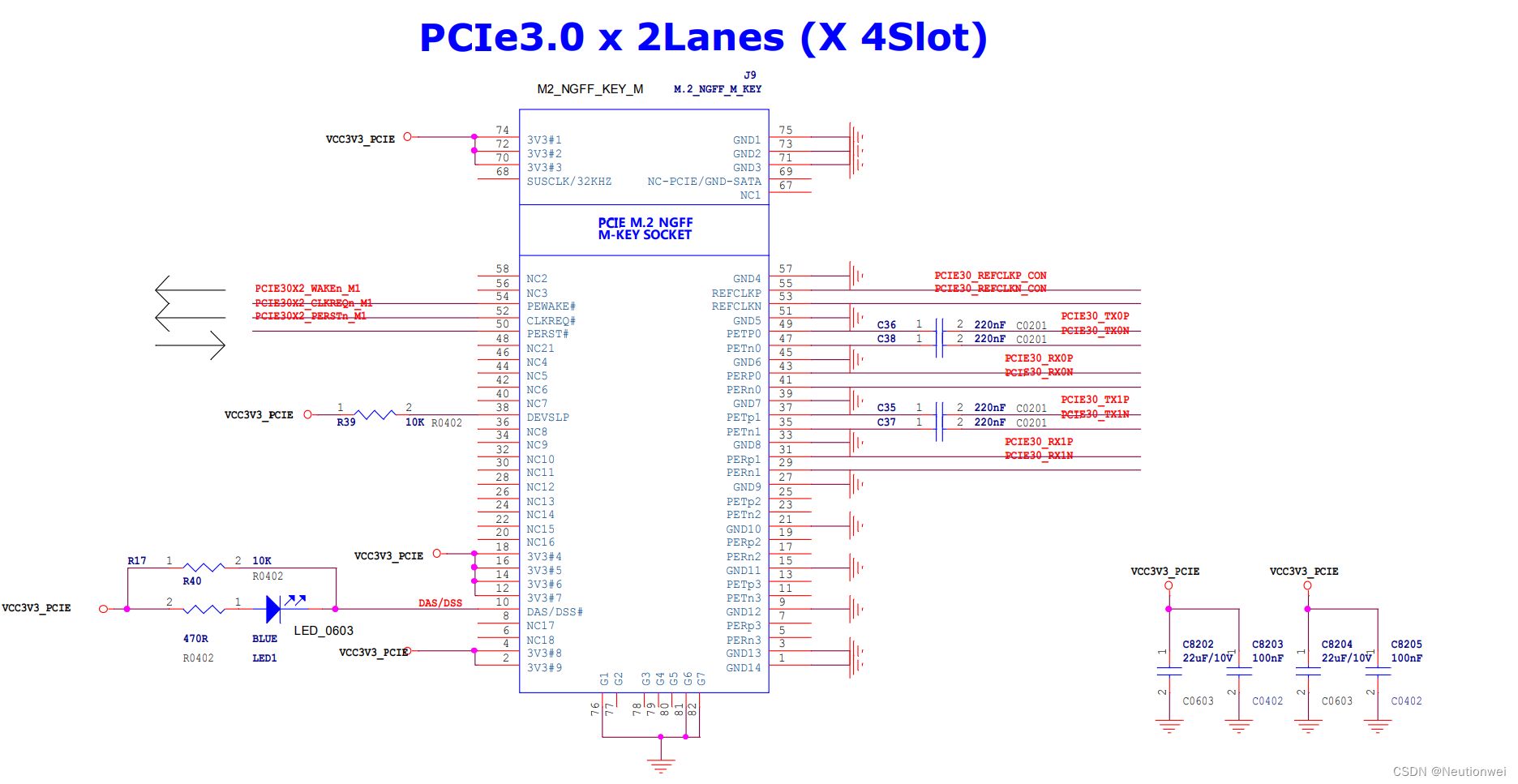
平台U-Boot 版本Linux SDK 版本RK356x2017.09v1.2.3文章目录 一、设备树与config配置二、pci命令的定义三、nvme命令的定义四、pci与nvme命令的用法3.1 pci总线扫描3.2 nvme设备信息3.3 nvme设备读写一、设备树与config配置 RK3568支持PCIe接口,例如ROC-RK3568-PC: 原理图如…...

微信头像昵称获取能力的变化导致了我半年没更新小程序
背景 2022年9月份,微信更改了获取头像昵称的规则,回收了原有 wx.getUserProfile 中的部分能力,为了减小对【微点记账】小程序的影响,长达半年未做任何更新,今天为了增加这个聊天机器人的功能,不得不重新查…...
【深度学习编译器系列】1. 为什么需要深度学习编译器?
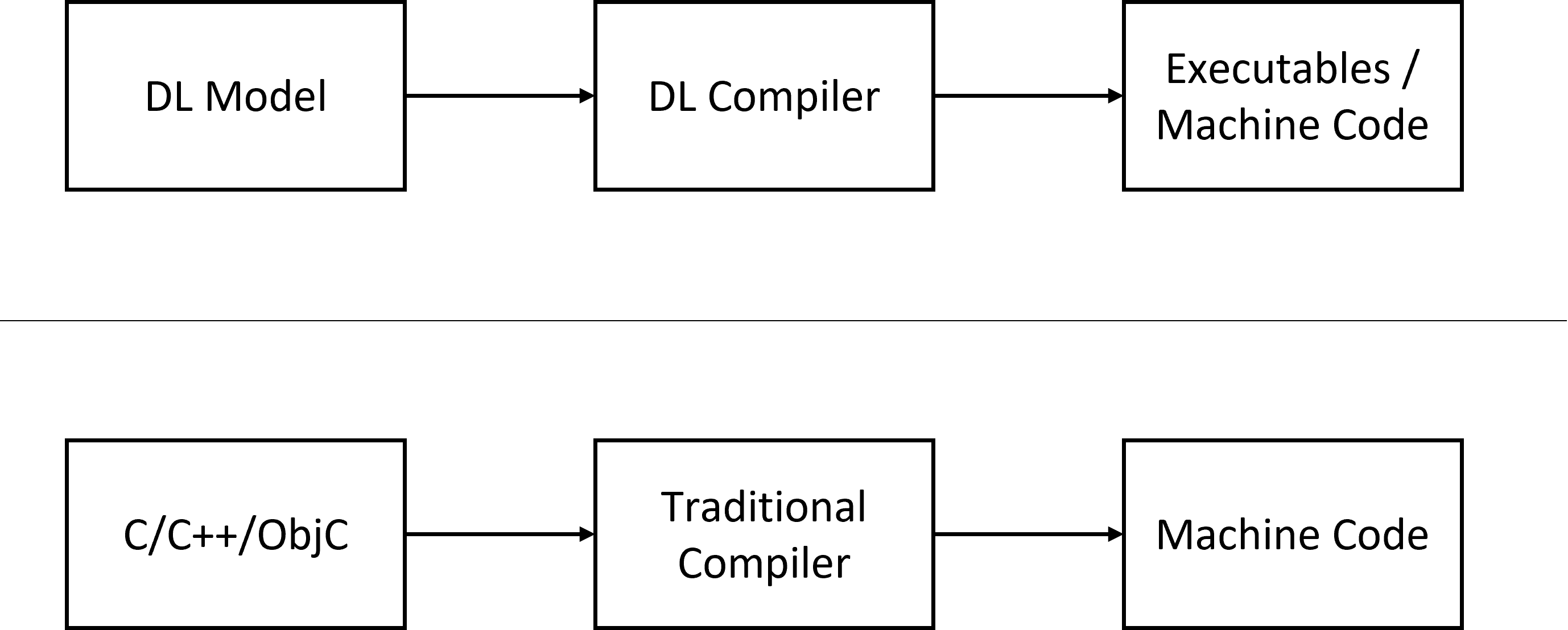
本系列是自学深度学习编译器过程中的一些笔记和总结,参考文献在文末。 1. 概述 深度学习(DL)编译器的产生有两方面的因素:深度学习模型的广泛应用,以及深度学习芯片的层出不穷。 一方面,我们现在有非常多…...
数据结构与算法总结整理(超级全的哦!)
数据结构与算法基础大O表示法时间复杂度大O表示法时间复杂度排序:最坏时间复杂度时间复杂度的几条基本计算规则内存工作原理什么是内存内存主要分为三种存储器随机存储器(RAM)只读存储器(ROM)高速缓存(Cach…...

DPDK — MALLOC 堆内存管理组件
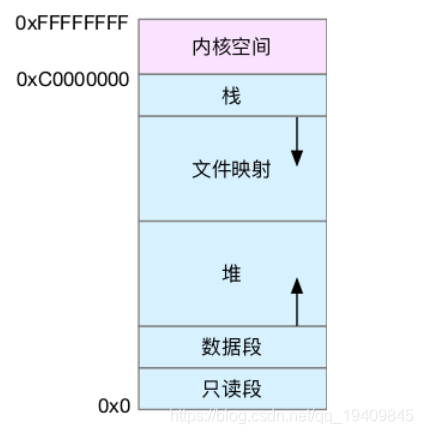
目录 文章目录 目录MALLOC 堆内存管理组件rte_malloc() 接口malloc_heap 结构体malloc_elem 结构体内存初始化流程内存申请流程内存释放流程MALLOC 堆内存管理组件 MALLOC(堆内存管理组件)基于 hugetlbfs 内核文件系统来实现,能够从 HugePage 中分配一块连续的物理大页内存…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

离线语音识别方案分析
随着人工智能技术的不断发展,语音识别技术也得到了广泛的应用,从智能家居到车载系统,语音识别正在改变我们与设备的交互方式。尤其是离线语音识别,由于其在没有网络连接的情况下仍然能提供稳定、准确的语音处理能力,广…...

DAY 26 函数专题1
函数定义与参数知识点回顾:1. 函数的定义2. 变量作用域:局部变量和全局变量3. 函数的参数类型:位置参数、默认参数、不定参数4. 传递参数的手段:关键词参数5 题目1:计算圆的面积 任务: 编写一…...

React从基础入门到高级实战:React 实战项目 - 项目五:微前端与模块化架构
React 实战项目:微前端与模块化架构 欢迎来到 React 开发教程专栏 的第 30 篇!在前 29 篇文章中,我们从 React 的基础概念逐步深入到高级技巧,涵盖了组件设计、状态管理、路由配置、性能优化和企业级应用等核心内容。这一次&…...

aardio 自动识别验证码输入
技术尝试 上周在发学习日志时有网友提议“在网页上识别验证码”,于是尝试整合图像识别与网页自动化技术,完成了这套模拟登录流程。核心思路是:截图验证码→OCR识别→自动填充表单→提交并验证结果。 代码在这里 import soImage; import we…...

大模型——基于Docker+DeepSeek+Dify :搭建企业级本地私有化知识库超详细教程
基于Docker+DeepSeek+Dify :搭建企业级本地私有化知识库超详细教程 下载安装Docker Docker官网:https://www.docker.com/ 自定义Docker安装路径 Docker默认安装在C盘,大小大概2.9G,做这行最忌讳的就是安装软件全装C盘,所以我调整了下安装路径。 新建安装目录:E:\MyS…...

表单设计器拖拽对象时添加属性
背景:因为项目需要。自写设计器。遇到的坑在此记录 使用的拖拽组件时vuedraggable。下面放上局部示例截图。 坑1。draggable标签在拖拽时可以获取到被拖拽的对象属性定义 要使用 :clone, 而不是clone。我想应该是因为draggable标签比较特。另外在使用**:clone时要将…...
