算法导论【分治思想】—大数乘法、矩阵相乘、残缺棋盘
这里写自定义目录标题
- 分治法概述
- 特点
- 大数相乘问题
- 分治算法
- 矩阵相乘
- 分治算法
- 残缺棋盘
- 分治算法
分治法概述
在分而治之的方法中,一个问题被划分为较小的问题,然后较小的问题被独立地解决,最后较小问题的解决方案被组合成一个大问题的解决。
通常,分治算法有三个部分:
- 分解:将问题划分为若干子问题,这些子问题是同一问题的较小实例。
- 解决:通过递归地解决子问题来征服它们。如果它们足够小,则将子问题作为基本情况解决。
- 合并:将子问题的解决方案合并为原始问题的解决方法。
特点
分治方法支持并行性,因为子问题是独立的。因此,使用该技术设计的算法可以在多处理器系统上或在不同的机器上同时运行。在这种方法中,大多数算法都是使用递归设计的,因此内存管理非常高。对于递归函数堆栈,需要存储函数状态。
大数相乘问题
-
输入:两个n位整数X和Y。
-
输出:X和Y的乘积。
-
示例:X=1980 Y=2315
-

-
这是你在小学学的算法。注意这需要O(n2) 时间
分治算法
-
按如下方式分解XY,得到一个新的计算公式,但这个公式仍然要计算:ac、ad、bc、bd四个乘式

-
因此它的递归式为:

-
运用主方法可以求出,递归式的解为T(n)=O(n2)。与原始方法相比,该方法没有显著改进。为了减少时间复杂性,我们必须减少乘法次数
-
修改计算公式如下:

-
最后两个XY乘法方案的复杂度为O(nlog3),但考虑到a+b,c+d可能得到n+1位的结果,这使得问题的规模更大,因此没有选择第三个方案。
-
可以列出如下递归式:

-
解得T(n)=O(nlog3)=O(n1.59)。
矩阵相乘
- 让我们考虑两个矩阵A和B。我们想通过乘以A和B来计算得到的矩阵C。
- 朴素方法是如果A=(aij)和B=(bij)是n×n的矩阵,那么在乘积C=A·B中,我们定义条目cij,对于i,j=1,2,。。。,n、 通过cij=∑k=1naik⋅bkjcij=\sum^n_{k=1}a_{ik}·b_{kj}cij=∑k=1naik⋅bkj。
- 我们必须计算n2个矩阵条目,每个条目都是n个值的总和。
- 我们假设整数运算需要O(1)时间。该算法中有三个for循环,一个嵌套在另一个循环中。因此,该算法需要O(n3)时间来执行

分治算法
下面是两个方阵相乘的简单除法。
- 将矩阵A和B分成4个子矩阵,大小为N/2×N/2,如下图所示。
- 递归计算以下值

- 在上述方法中,我们对大小为N/2×N/2的矩阵进行了8次乘法运算和4次加法运算。两个矩阵相加需要O(n2) 时间。因此,时间复杂度为T(n)= 8T(n/2)+O(n2) 。根据主定理,上述方法的时间复杂度为 O(n3),不幸的是,这与上述朴素方法相同。简单的分治也会导致O(n3),有更好的方法吗?
- 在上述分治的方法中,高时间复杂度的主要组成部分是8个递归调用。Strassens方法的思想是将递归调用的数量减少到7。Strassens方法与上述简单除法和征服法相似,因为该方法也将矩阵划分为大小为N/2×N/2的子矩阵,如上图所示,但在Strassens法中,使用以下公式计算结果的四个子矩阵。
- Strassen算法定义了新的矩阵

- 仅使用7次乘法(对每个MkM_kMk)而不是8次。我们现在可以用Mk表示Ci:

- 两个矩阵的加法和减法需要O(n2)时间。因此,时间复杂性可以写成:

- 根据主定理,上述方法的时间复杂度为O(nlog7),近似于O(n2.8074)
-
Hopcroft和Kerr证明(1971)在两个2×2矩阵的乘法中需要7次乘法。因此,为了进一步提高矩阵乘法复杂度的时间,它不能再基于计算2×2矩阵的7倍乘法的方法。也许应该研究3×3或5×5矩阵的更好算法。目前,最佳计算时间上限为O(n 2.376)。
残缺棋盘
- 定义:有缺陷的棋盘是一块2k×2k的正方形棋盘,正好有一个有缺陷的正方形
- 例子:

- 要求用一种化合物来平铺(覆盖)所有非残缺方格。
- 化合物是一种L形物体,可以覆盖棋盘的三个方格。
- 有四个方向:

分治算法
- 分成四个小棋盘。
- 其中一个是有缺陷的棋盘。

- 通过在其他三个棋盘的共同角落放置一个三分之一,使其有缺陷。
- 递归平铺四个有缺陷的棋盘

- 设n=2k,d是常数。 设t(k)是平铺2k×2k有缺陷棋盘所花费的时间。然后

- 这里,c是常数,表示为化合物找到合适位置和旋转化合物以获得所需形状所花费的时间。

- 由于每个网格必须花费θ(1)时间来放置每个化合物,因此不可能得到一个更快的算法来解决这个问题
相关文章:

算法导论【分治思想】—大数乘法、矩阵相乘、残缺棋盘
这里写自定义目录标题分治法概述特点大数相乘问题分治算法矩阵相乘分治算法残缺棋盘分治算法分治法概述 在分而治之的方法中,一个问题被划分为较小的问题,然后较小的问题被独立地解决,最后较小问题的解决方案被组合成一个大问题的解决。 通常…...
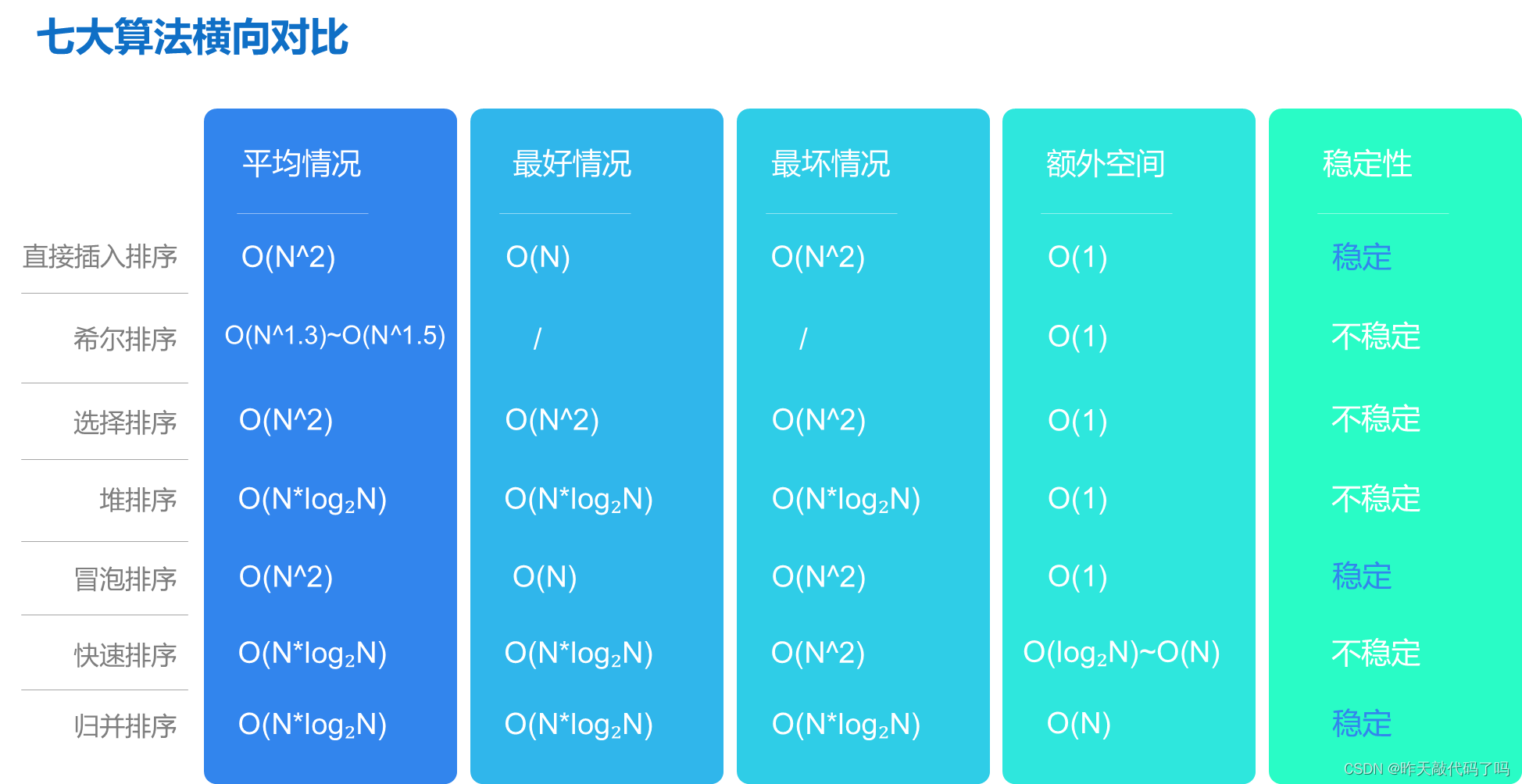
Java【七大排序】算法详细图解,一篇文章吃透
文章目录一、排序相关概念二、七大排序1,直接插入排序2,希尔排序3,选择排序4,堆排序5,冒泡排序5.1冒泡排序的优化6,快速排序6.1 快速排序的优化7,归并排序三、排序算法总体分析对比总结提示&…...

Autosar OS IOC
Inter-OS-Application Communicator 背景和基本原理General purposeIOC functionalityCommunicationNotificationIOC interface背景和基本原理 The IOC implementation shall be part of the Operating System IOC和操作系统紧密相关,是操作系统实现的一部分 The IO…...
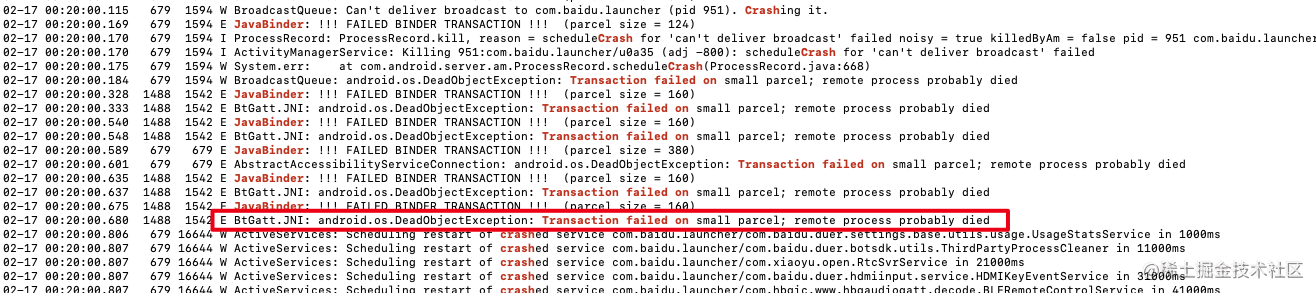
记录一次Binder内存相关的问题导致APP被杀的BUG排查过程
事情的起因的QA压测过程发生进程号变更,怀疑APP被杀掉过,于是开始看日志 APP的压测平台会上报进程号变更时间点,发现是在临晨12:20分,先大概确定在哪个日志文件去找关键信息一开始怀疑是crash,然后就在日志…...
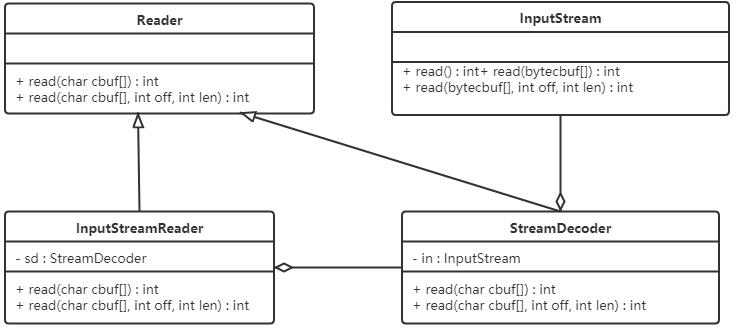
设计模式(十)----结构型模式之适配器模式
1、概述 如果去欧洲国家去旅游的话,他们的插座如下图最左边,是欧洲标准。而我们使用的插头如下图最右边的。因此我们的笔记本电脑,手机在当地不能直接充电。所以就需要一个插座转换器,转换器第1面插入当地的插座,第2面…...
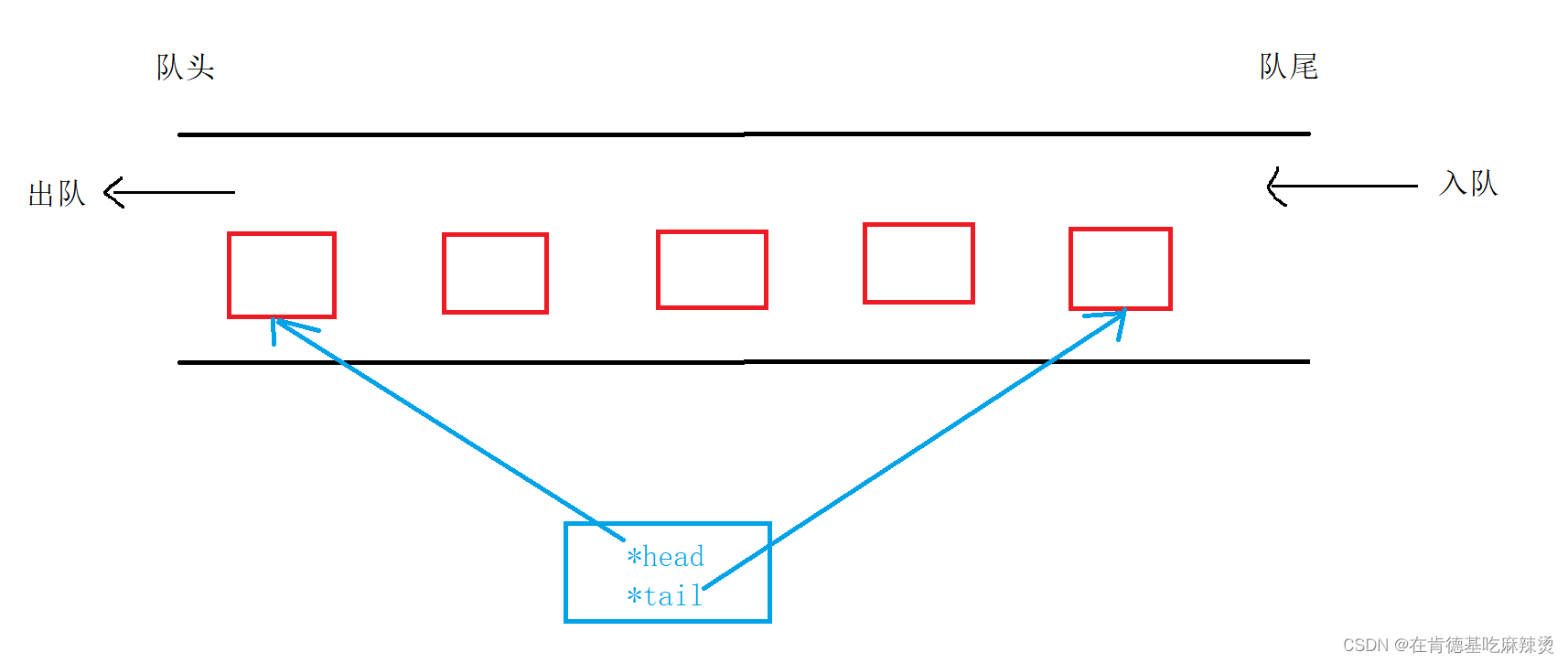
【数据结构】——队列
文章目录前言一.什么是队列,队列的特点二、队列相关操作队列的相关操作声明队列的创建1.队列的初始化2.对队列进行销毁3.判断队列是否为空队列4.入队操作5.出队操作6.取出队头数据7. 取出队尾数据8.计算队伍的人数总结前言 本文章讲述的是数据结构的特殊线性表——…...
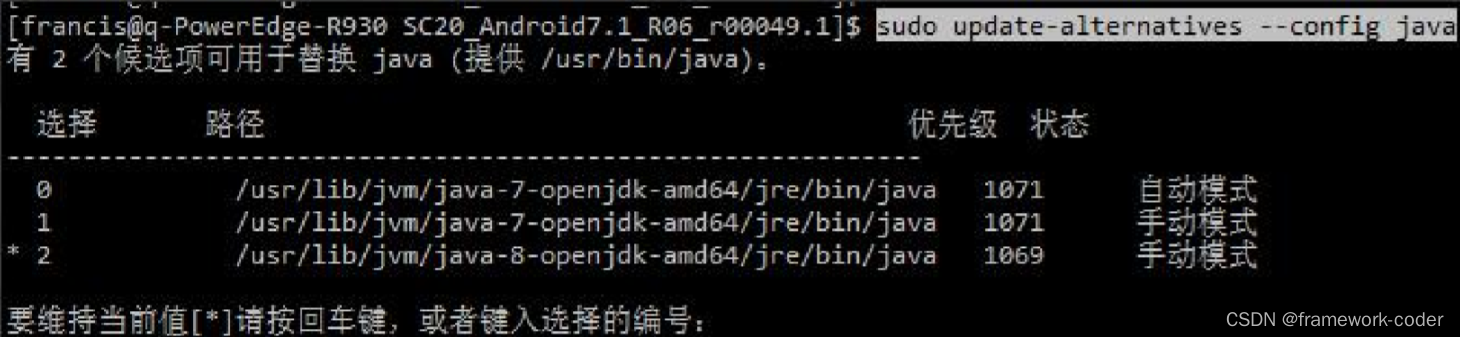
Android OTA升级常见问题的解决方法
1.1 多服务器编译 OTA 报错 Android7 以后引入了 jack-server 功能,也导致在公共服务器上 编译 Android7 以上的版本时,会出现 j ack-server 报错问题。 在多用户服务器上 编译 dist 时 会出现编译过程中 会将 port_service 和 port_admin 改为 默认的 …...
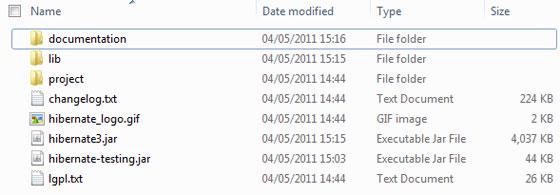
说说Hibernate
当你在实战项目中需要用到SSH时, 如果你之前只用过Mybatis那自然是不能解决问题的, 因为在很多银行类金融类项目中你可能会使用到Hibernate, 那么关于Hibernate你应该要了解什么呢, 本篇文章就以学习Hibernate框架为目的, 巩固在工作中可能需要用到的这种ORM技术, 同时也欢迎家…...

目标检测论文阅读:DETR算法笔记
标题:End-to-End Object Detection with Transformers 会议:ECCV2020 论文地址:https://link.springer.com/10.1007/978-3-030-58452-8_13 官方代码:https://github.com/facebookresearch/detr 作者单位:巴黎第九大学、…...

Golang sync.Once 源码浅析
本文分析了Golang sync.Once 源码,并由此引申,简单讨论了单例模式的实现、 atomic 包的作用和 Java volatile 的使用。 sync.Once 使用例子 sync.Once 用于保证一个函数只被调用一次。它可以用于实现单例模式。 有如下类型: type instanc…...
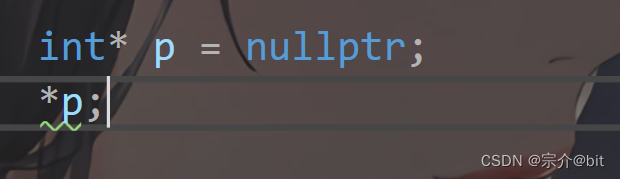
C++面向对象(上)
文章目录前言1.面向过程和面向对象初步认识2.引入类的概念1.概念与用法2.类的访问限定符及封装3.类的作用域和实例化4.类的大小计算5.this指针3.总结前言 本文将对C面向对象进行初步介绍,引入类和对象的概念。围绕类和对象介绍一些基础知识,为以后深入学…...

经常用但是不知道什么是BFC?
BFC学习 block formatting context 块级格式上下文 简单理解: 一个独立容器,内部布局不会受到外面的影响 形成条件: 1.浮动元素:float除none之外的值 2.绝对定位:position:absolute,fixed 3.display:inline-blo…...

GO的临时对象池sync.Pool
GO的临时对象池sync.Pool 文章目录GO的临时对象池sync.Pool一、临时对象池:sync.Pool1.1 临时对象的特点1.2 临时对象池的用途1.3 sync.Pool 的用法二、临时对象池中的值会被及时清理掉2.1 池清理函数2.2 池汇总列表2.3 临时对象池存储值所用的数据结构2.4 临时对象…...
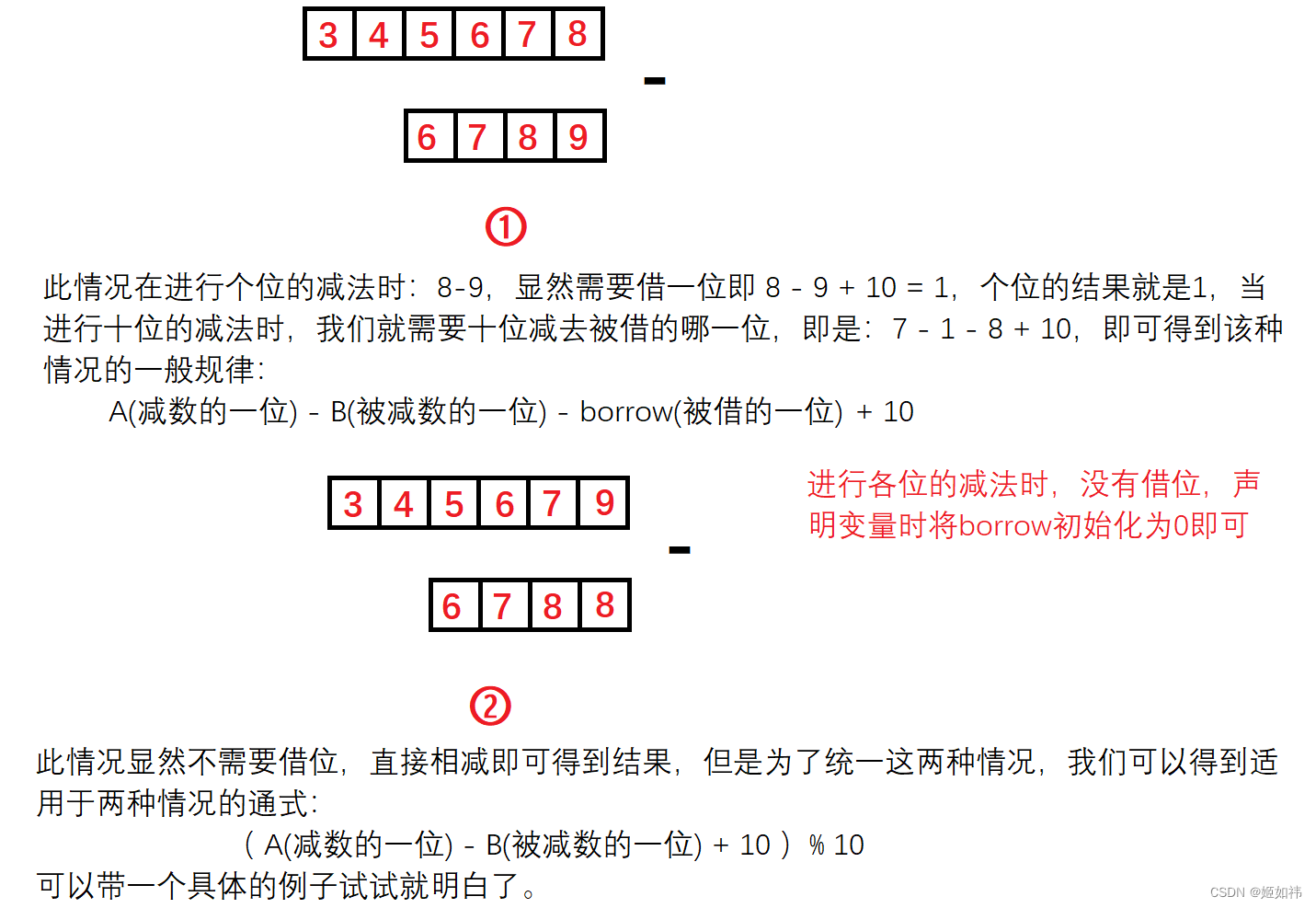
高精度算法一
目录 1. 基础知识 2. 大整数 大整数 3. 大整数 - 大整数 1. 基础知识 利用计算机进行数值计算,有时会遇到这样的问题:有些计算要求精度高,希望计算的数的位数可达几十位甚至几百位,虽然计算机的计算精度也算较高了,…...

2023年全国最新食品安全管理员精选真题及答案1
百分百题库提供食品安全管理员考试试题、食品安全员考试预测题、食品安全管理员考试真题、食品安全员证考试题库等,提供在线做题刷题,在线模拟考试,助你考试轻松过关。 11.预包装食品的标签内容应使用规范的汉字,但可以同时使用&a…...
C++入门:引用
目录 一. 什么是引用 1.1 引用的概念 1.2 引用的定义 二. 引用的性质和用途 2.1 引用的三大主要性质 2.2 引用的主要应用 三. 引用的效率测试 3.1 传值调用和传引用调用的效率对比 3.2 值返回和引用返回的效率对比 四. 常引用 4.1 权限放大和权限缩小问题 4.2 跨…...
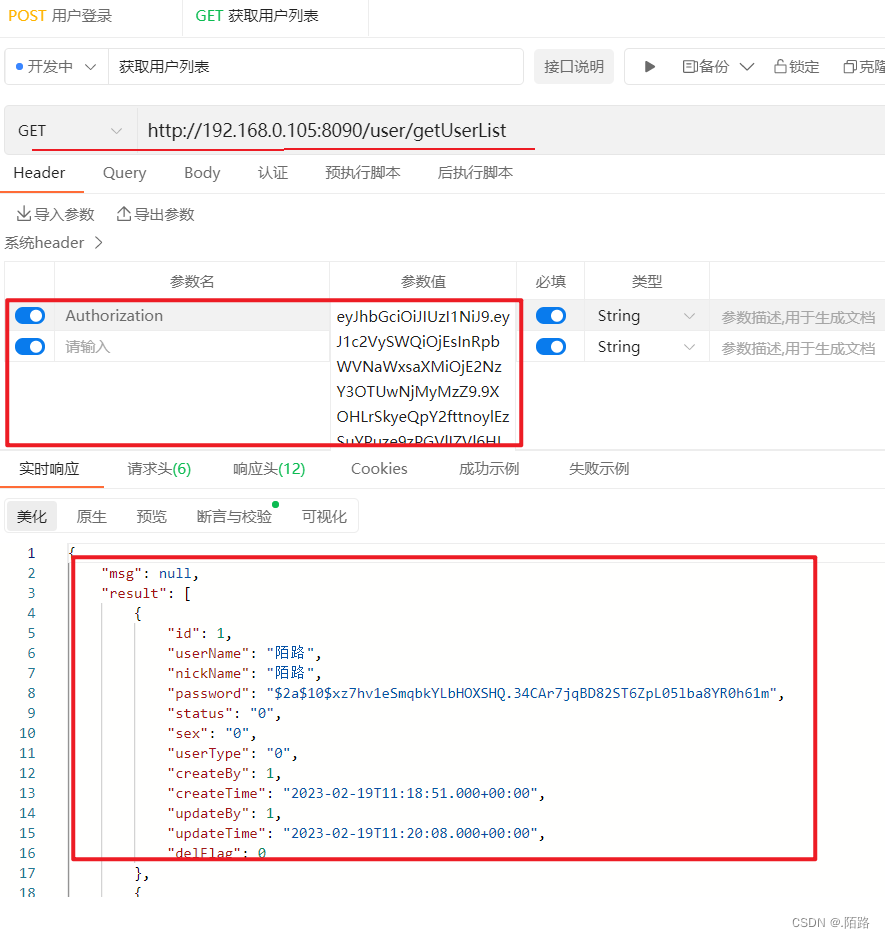
SpringSecurity的权限校验详解说明(附完整代码)
说明 SpringSecurity的权限校是基于SpringSecurity的安全认证的详解说明(附完整代码) (https://blog.csdn.net/qq_51076413/article/details/129102660)的讲解,如果不了解SpringSecurity是怎么认证,请先看下【SpringSecurity的安…...
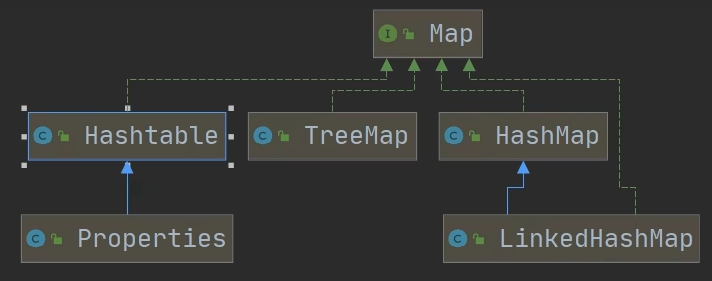
Java-集合(5)
Map接口 JDK8 Map接口实现子类的特点 Map和Collection是并列关系,Map用于保存具有映射关系的数据:Key-ValueMap中的key和value可以是任何引用类型的数据,会封装到HashMap$Node对象中Map中的key不允许重复,原因和HashSet一样Map…...
设计定型阶段)
研制过程评审活动(四)设计定型阶段
1、设计定型阶段主要任务 设计定型的主要任务是对武器装备性能和使用要求进行全面考核,以确认产品是否达到《研制任务书》和《研制合同》的要求。 设计定型阶段应最终确定《产品规范》、《工艺规范》和《材料规范》的正式版本,并形成正式的全套生产图样、有关技术文件及目…...
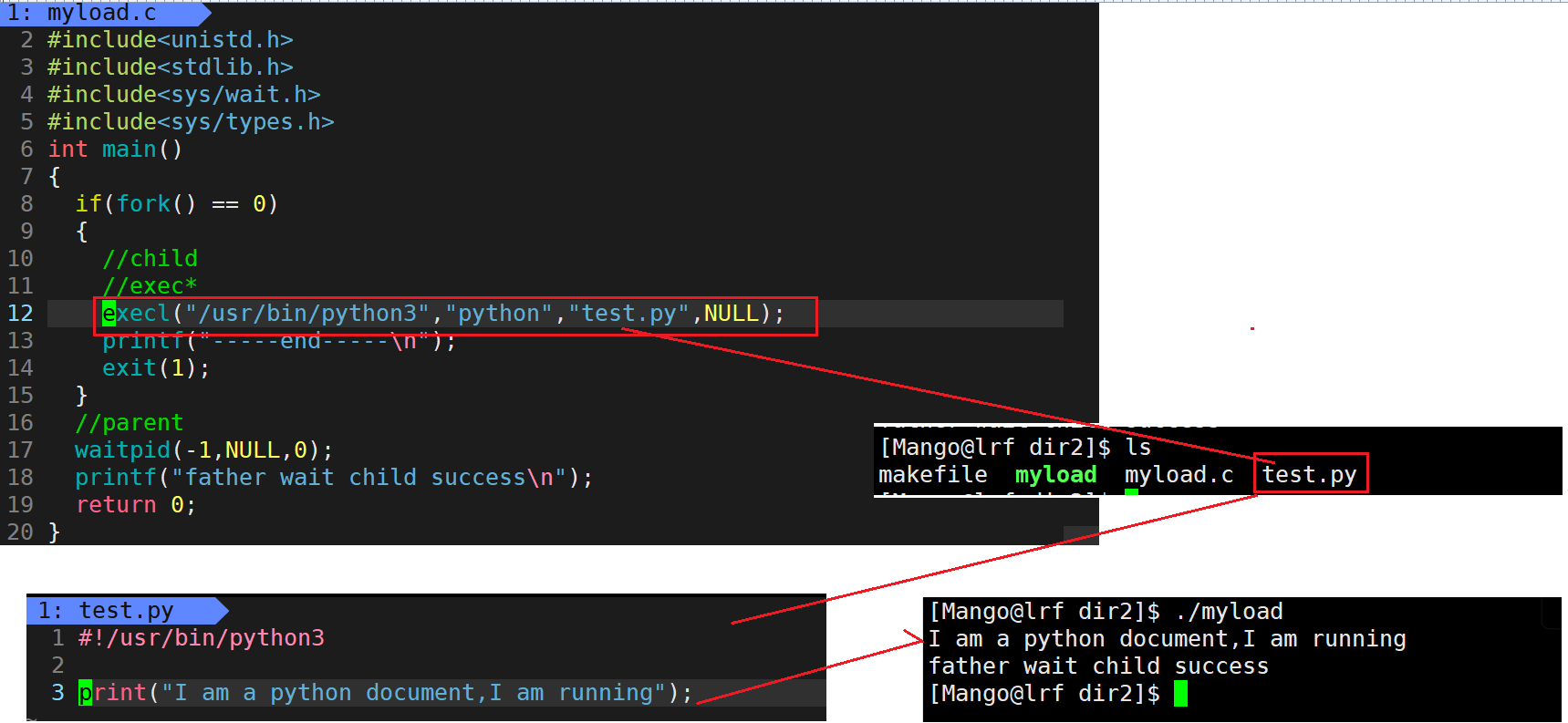
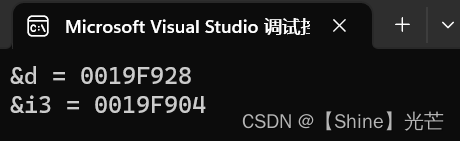
【Linux】进程替换
文章目录进程程序替换替换原理替换函数函数返回值函数命名理解在makefile文件中一次生成两个可执行文件总结:程序替换时运行其它语言程序进程程序替换 程序要运行要先加载到内存当中 , 如何做到? 加载器加载进来,然后程序替换 为什么? ->冯诺依曼 因为CPU读取数据的时候只…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...
