关于3D位姿旋转
一. 主动旋转和被动旋转
1. active rotation 主动旋转
站在坐标系的位置看旋转目标物:目标物主动发生旋转。
2. passive rotation 被动旋转
站在旋转目标物的位置看坐标系: 坐标系发生旋转,相当于目标物在坐标系内的位置被动地发生了旋转。
主动旋转的旋转矩阵和被动旋转的旋转矩阵是互相为逆的。
二. 内旋和外旋
1. intrinsic rotations 动坐标系旋转,即坐标系原点固定于目标物内部,当目标物发生旋转,坐标系也跟着做刚性旋转。
2. extrinsic rotations 固定坐标系旋转,即坐标系位于外部参考点,当目标物旋转,坐标系不动。
欧拉角描述物体姿态时,必须先确定是基于内旋坐标系还是外旋坐标系。
三. 3D旋转库
使用python的朋友,可以直接安装pytransform3d库就可以实现任意3d姿态的变换,里面有各种欧拉角,旋转矩阵,四元数之间的相互转换。官方网址为:pytransform3d — pytransform3d 3.4.0 documentation
如果使用c/c++,则可以从pytransform3d库中的提取关键部分,改写为c/c++,以供调用。下面就将这些欧拉角转换部分提取出来,以源码形式贴出来,供有需要的朋友使用(下面欧拉角是弧度制表示的,使用时需要注意):
// transform3d.h
#ifndef __TRANSFORM_3D_H__
#define __TRANSFORM_3D_H__
//https://dfki-ric.github.io/pytransform3d/euler_angles.html
typedef float MATRIX_SO3_F[9];
typedef float MATRIX_SE3_F[16];
typedef float MATRIX_EULER_F[3];
typedef float MATRIX_QUATERNION_F[4];
typedef float VECTOR3F[3];bool matrix_so3_inverse_f(const MATRIX_SO3_F r, MATRIX_SO3_F r_t);bool matrix_se3_inverse_f(const MATRIX_SE3_F t, MATRIX_SE3_F t_inv);void matrix_3x3_product_f(const MATRIX_SO3_F r1, const MATRIX_SO3_F r2, MATRIX_SO3_F r);void matrix_4x4_product_f(const MATRIX_SE3_F se1, const MATRIX_SE3_F se2, MATRIX_SE3_F se);bool active_matrix_from_angle(int basis, float angle, MATRIX_SO3_F so);void matrix_so3_from_se3_f(const MATRIX_SE3_F se, MATRIX_SO3_F so, VECTOR3F xyz);void matrix_se3_from_so3_f(const MATRIX_SO3_F so, const VECTOR3F xyz, MATRIX_SE3_F se);bool general_intrinsic_euler_from_active_matrix(const MATRIX_SO3_F R, const VECTOR3F n1, const VECTOR3F n2, const VECTOR3F n3, bool proper_euler, MATRIX_EULER_F euler, bool strict_check = true);bool euler_from_matrix(const MATRIX_SO3_F R, int i, int j, int k, MATRIX_EULER_F result, bool extrinsic, bool strict_check = true);bool matrix_from_euler(const MATRIX_EULER_F e, int i, int j, int k, MATRIX_SO3_F result, bool extrinsic);bool quaternion_from_angle(int basis, float angle, MATRIX_QUATERNION_F quat);bool quaternion_from_euler(MATRIX_EULER_F e, int i, int j, int k, MATRIX_QUATERNION_F res, bool extrinsic);bool euler_from_quaternion(const MATRIX_QUATERNION_F q, int i, int j, int k, MATRIX_EULER_F euler, bool extrinsic);bool matrix_from_quaternion(const MATRIX_QUATERNION_F q, MATRIX_SO3_F R);bool quaternion_from_matrix(const MATRIX_SO3_F R, MATRIX_QUATERNION_F res, bool strict_check = true);bool active_matrix_from_intrinsic_euler_xzx(const MATRIX_EULER_F e, MATRIX_SO3_F R);bool active_matrix_from_extrinsic_euler_xzx(const MATRIX_EULER_F e, MATRIX_SO3_F R);bool active_matrix_from_intrinsic_euler_xyx(const MATRIX_EULER_F e, MATRIX_SO3_F R);bool active_matrix_from_extrinsic_euler_xyx(const MATRIX_EULER_F e, MATRIX_SO3_F R);bool active_matrix_from_intrinsic_euler_yxy(const MATRIX_EULER_F e, MATRIX_SO3_F R);bool active_matrix_from_extrinsic_euler_yxy(const MATRIX_EULER_F e, MATRIX_SO3_F R);bool active_matrix_from_intrinsic_euler_yzy(const MATRIX_EULER_F e, MATRIX_SO3_F R);bool active_matrix_from_extrinsic_euler_yzy(const MATRIX_EULER_F e, MATRIX_SO3_F R);bool active_matrix_from_intrinsic_euler_zyz(const MATRIX_EULER_F e, MATRIX_SO3_F R);bool active_matrix_from_extrinsic_euler_zyz(const MATRIX_EULER_F e, MATRIX_SO3_F R);bool active_matrix_from_intrinsic_euler_zxz(const MATRIX_EULER_F e, MATRIX_SO3_F R);bool active_matrix_from_extrinsic_euler_zxz(const MATRIX_EULER_F e, MATRIX_SO3_F R);bool active_matrix_from_intrinsic_euler_xzy(const MATRIX_EULER_F e, MATRIX_SO3_F R);bool active_matrix_from_extrinsic_euler_xzy(const MATRIX_EULER_F e, MATRIX_SO3_F R);bool active_matrix_from_intrinsic_euler_xyz(const MATRIX_EULER_F e, MATRIX_SO3_F R);bool active_matrix_from_extrinsic_euler_xyz(const MATRIX_EULER_F e, MATRIX_SO3_F R);bool active_matrix_from_intrinsic_euler_yxz(const MATRIX_EULER_F e, MATRIX_SO3_F R);bool active_matrix_from_extrinsic_euler_yxz(const MATRIX_EULER_F e, MATRIX_SO3_F R);bool active_matrix_from_intrinsic_euler_yzx(const MATRIX_EULER_F e, MATRIX_SO3_F R);bool active_matrix_from_extrinsic_euler_yzx(const MATRIX_EULER_F e, MATRIX_SO3_F R);bool active_matrix_from_intrinsic_euler_zyx(const MATRIX_EULER_F e, MATRIX_SO3_F R);bool active_matrix_from_extrinsic_euler_zyx(const MATRIX_EULER_F e, MATRIX_SO3_F R);bool active_matrix_from_intrinsic_euler_zxy(const MATRIX_EULER_F e, MATRIX_SO3_F R);bool active_matrix_from_extrinsic_euler_zxy(const MATRIX_EULER_F e, MATRIX_SO3_F R);bool active_matrix_from_extrinsic_roll_pitch_yaw(const VECTOR3F rpy, MATRIX_SO3_F R);bool intrinsic_euler_xzx_from_active_matrix(const MATRIX_SO3_F R, MATRIX_EULER_F euler, bool strict_check = true);bool extrinsic_euler_xzx_from_active_matrix(const MATRIX_SO3_F R, MATRIX_EULER_F euler, bool strict_check = true);bool intrinsic_euler_xyx_from_active_matrix(const MATRIX_SO3_F R, MATRIX_EULER_F euler, bool strict_check = true);bool extrinsic_euler_xyx_from_active_matrix(const MATRIX_SO3_F R, MATRIX_EULER_F euler, bool strict_check = true);bool intrinsic_euler_yxy_from_active_matrix(const MATRIX_SO3_F R, MATRIX_EULER_F euler, bool strict_check = true);bool extrinsic_euler_yxy_from_active_matrix(const MATRIX_SO3_F R, MATRIX_EULER_F euler, bool strict_check = true);bool intrinsic_euler_yzy_from_active_matrix(const MATRIX_SO3_F R, MATRIX_EULER_F euler, bool strict_check = true);bool extrinsic_euler_yzy_from_active_matrix(const MATRIX_SO3_F R, MATRIX_EULER_F euler, bool strict_check = true);bool intrinsic_euler_zyz_from_active_matrix(const MATRIX_SO3_F R, MATRIX_EULER_F euler, bool strict_check = true);bool extrinsic_euler_zyz_from_active_matrix(const MATRIX_SO3_F R, MATRIX_EULER_F euler, bool strict_check = true);bool intrinsic_euler_zxz_from_active_matrix(const MATRIX_SO3_F R, MATRIX_EULER_F euler, bool strict_check = true);bool extrinsic_euler_zxz_from_active_matrix(const MATRIX_SO3_F R, MATRIX_EULER_F euler, bool strict_check = true);bool intrinsic_euler_xzy_from_active_matrix(const MATRIX_SO3_F R, MATRIX_EULER_F euler, bool strict_check = true);bool extrinsic_euler_xzy_from_active_matrix(const MATRIX_SO3_F R, MATRIX_EULER_F euler, bool strict_check = true);bool intrinsic_euler_xyz_from_active_matrix(const MATRIX_SO3_F R, MATRIX_EULER_F euler, bool strict_check = true);bool extrinsic_euler_xyz_from_active_matrix(const MATRIX_SO3_F R, MATRIX_EULER_F euler, bool strict_check = true);bool intrinsic_euler_yxz_from_active_matrix(const MATRIX_SO3_F R, MATRIX_EULER_F euler, bool strict_check = true);bool extrinsic_euler_yxz_from_active_matrix(const MATRIX_SO3_F R, MATRIX_EULER_F euler, bool strict_check = true);bool intrinsic_euler_yzx_from_active_matrix(const MATRIX_SO3_F R, MATRIX_EULER_F euler, bool strict_check = true);bool extrinsic_euler_yzx_from_active_matrix(const MATRIX_SO3_F R, MATRIX_EULER_F euler, bool strict_check = true);bool intrinsic_euler_zyx_from_active_matrix(const MATRIX_SO3_F R, MATRIX_EULER_F euler, bool strict_check = true);bool extrinsic_euler_zyx_from_active_matrix(const MATRIX_SO3_F R, MATRIX_EULER_F euler, bool strict_check = true);bool intrinsic_euler_zxy_from_active_matrix(const MATRIX_SO3_F R, MATRIX_EULER_F euler, bool strict_check = true);bool extrinsic_euler_zxy_from_active_matrix(const MATRIX_SO3_F R, MATRIX_EULER_F euler, bool strict_check = true);#endif
// transform3d.cpp
#include "transform3d.h"
#include <math.h>
#include <string.h>
#include <iostream>
//#define PI acos(-1)
#define PI 3.14159265358979323846const VECTOR3F unitxyz[3] = { { 1.0f, 0.0f, 0.0f },
{ 0.0f, 1.0f, 0.0f },
{ 0.0f, 0.0f, 1.0f } };void matrix_3x3_product_f(const MATRIX_SO3_F r1, const MATRIX_SO3_F r2, MATRIX_SO3_F r)
{r[0] = r1[0] * r2[0] + r1[1] * r2[3] + r1[2] * r2[6];r[1] = r1[0] * r2[1] + r1[1] * r2[4] + r1[2] * r2[7];r[2] = r1[0] * r2[2] + r1[1] * r2[5] + r1[2] * r2[8];r[3] = r1[3] * r2[0] + r1[4] * r2[3] + r1[5] * r2[6];r[4] = r1[3] * r2[1] + r1[4] * r2[4] + r1[5] * r2[7];r[5] = r1[3] * r2[2] + r1[4] * r2[5] + r1[5] * r2[8];r[6] = r1[6] * r2[0] + r1[7] * r2[3] + r1[8] * r2[6];r[7] = r1[6] * r2[1] + r1[7] * r2[4] + r1[8] * r2[7];r[8] = r1[6] * r2[2] + r1[7] * r2[5] + r1[8] * r2[8];return;
}void matrix_4x4_product_f(const MATRIX_SE3_F se1, const MATRIX_SE3_F se2, MATRIX_SE3_F se)
{se[0] = se1[0] * se2[0] + se1[1] * se2[4] + se1[2] * se2[8] + se1[3] * se2[12];se[1] = se1[0] * se2[1] + se1[1] * se2[5] + se1[2] * se2[9] + se1[3] * se2[13];se[2] = se1[0] * se2[2] + se1[1] * se2[6] + se1[2] * se2[10] + se1[3] * se2[14];se[3] = se1[0] * se2[3] + se1[1] * se2[7] + se1[2] * se2[11] + se1[3] * se2[15];se[4] = se1[4] * se2[0] + se1[5] * se2[4] + se1[6] * se2[8] + se1[7] * se2[12];se[5] = se1[4] * se2[1] + se1[5] * se2[5] + se1[6] * se2[9] + se1[7] * se2[13];se[6] = se1[4] * se2[2] + se1[5] * se2[6] + se1[6] * se2[10] + se1[7] * se2[14];se[7] = se1[4] * se2[3] + se1[5] * se2[7] + se1[6] * se2[11] + se1[7] * se2[15];se[8] = se1[8] * se2[0] + se1[9] * se2[4] + se1[10] * se2[8] + se1[11] * se2[12];se[9] = se1[8] * se2[1] + se1[9] * se2[5] + se1[10] * se2[9] + se1[11] * se2[13];se[10] = se1[8] * se2[2] + se1[9] * se2[6] + se1[10] * se2[10] + se1[11] * se2[14];se[11] = se1[8] * se2[3] + se1[9] * se2[7] + se1[10] * se2[11] + se1[11] * se2[15];se[12] = se1[12] * se2[0] + se1[13] * se2[4] + se1[14] * se2[8] + se1[15] * se2[12];se[13] = se1[12] * se2[1] + se1[13] * se2[5] + se1[14] * se2[9] + se1[15] * se2[13];se[14] = se1[12] * se2[2] + se1[13] * se2[6] + se1[14] * se2[10] + se1[15] * se2[14];se[15] = se1[12] * se2[3] + se1[13] * se2[7] + se1[14] * se2[11] + se1[15] * se2[15];return;
}void matrix_3x3_transpose_f(const MATRIX_SO3_F r1, MATRIX_SO3_F r)
{r[0] = r1[0];r[1] = r1[3];r[2] = r1[6];r[3] = r1[1];r[4] = r1[4];r[5] = r1[7];r[6] = r1[2];r[7] = r1[5];r[8] = r1[8];return;
}void matrix_3x1_cross_f(const MATRIX_EULER_F r1, const MATRIX_EULER_F r2, MATRIX_EULER_F r)
{r[0] = r1[1] * r2[2] - r1[2] * r2[1];r[1] = r1[2] * r2[0] - r1[0] * r2[2];r[2] = r1[0] * r2[1] - r1[1] * r2[0];return;
}float matrix_3x3_determinants_f(const MATRIX_SO3_F r1)
{float res = 0.0f;res = r1[0] * r1[4] * r1[8] + r1[2] * r1[5] * r1[6] + r1[3] * r1[7] * r1[2];res = res - r1[2] * r1[4] * r1[6] - r1[1] * r1[3] * r1[8] - r1[5] * r1[7] * r1[0];return res;
}void matrix_so3_from_se3_f(const MATRIX_SE3_F se, MATRIX_SO3_F so, VECTOR3F xyz)
{so[0] = se[0];so[1] = se[1];so[2] = se[2];xyz[0] = se[3];so[3] = se[4];so[4] = se[5];so[5] = se[6];xyz[1] = se[7];so[6] = se[8];so[7] = se[9];so[8] = se[10];xyz[2] = se[11];return;
}void matrix_se3_from_so3_f(const MATRIX_SO3_F so, const VECTOR3F xyz, MATRIX_SE3_F se)
{se[0] = so[0];se[1] = so[1];se[2] = so[2];se[3] = xyz[0];se[4] = so[3];se[5] = so[4];se[6] = so[5];se[7] = xyz[1];se[8] = so[6];se[9] = so[7];se[10] = so[8];se[11] = xyz[2];se[12] = 0.0f;se[13] = 0.0f;se[14] = 0.0f;se[15] = 1.0f;return;
}float norm_angle(float angle)
{/*"""Normalize angle to (-pi, pi].Parameters----------a : float or array - like, shape(n, )Angle(s) in radiansReturns------ -a_norm : float or array - like, shape(n, )Normalized angle(s) in radians"""*/float mod = 0.0f;int exp = int((PI - angle) / (2.0f*PI));if (exp < 0)mod = 2.0f*PI*(1 - exp) - (PI - angle);else if (exp == 0)mod = (PI - angle);elsemod = PI - angle - 2.0f*PI*exp;return PI - mod;
}bool check_matrix(const MATRIX_SO3_F R, bool strict_check, float tolerance = 1e-6)
{MATRIX_SO3_F RT = {}, RRT = {};matrix_3x3_transpose_f(R, RT);matrix_3x3_product_f(R, RT, RRT);bool ok = true;ok = ok && abs(RRT[0] - 1.0f)<tolerance;ok = ok && abs(RRT[4] - 1.0f)<tolerance;ok = ok && abs(RRT[8] - 1.0f)<tolerance;ok = ok && abs(RRT[1] - 0.0f)<tolerance;ok = ok && abs(RRT[2] - 0.0f)<tolerance;ok = ok && abs(RRT[3] - 0.0f)<tolerance;ok = ok && abs(RRT[5] - 0.0f)<tolerance;ok = ok && abs(RRT[6] - 0.0f)<tolerance;ok = ok && abs(RRT[7] - 0.0f)<tolerance;if (!ok){if (strict_check)return false;//printf("Warning: Expected rotation matrix, but it failed the test for inversion by transposition.\n");}float R_det = matrix_3x3_determinants_f(R);if (R_det < 0.0){if (strict_check)return false;//printf("Warning: Expected rotation matrix, but it failed the test for the determinant.\n");}return true;
}bool matrix_so3_inverse_f(const MATRIX_SO3_F r, MATRIX_SO3_F r_t)
{bool ret = check_matrix(r, false);if (!ret)return false;MATRIX_SO3_F r_t_tmp = {};r_t_tmp[0] = r[0];r_t_tmp[3] = r[1];r_t_tmp[6] = r[2];r_t_tmp[1] = r[3];r_t_tmp[4] = r[4];r_t_tmp[7] = r[5];r_t_tmp[2] = r[6];r_t_tmp[5] = r[7];r_t_tmp[8] = r[8];memcpy(r_t, r_t_tmp, sizeof(MATRIX_SO3_F));return true;
}bool matrix_se3_inverse_f(const MATRIX_SE3_F t, MATRIX_SE3_F t_inv)
{MATRIX_SO3_F r = {};MATRIX_SO3_F r_t = {};VECTOR3F p = {};matrix_so3_from_se3_f(t, r, p);bool ret = matrix_so3_inverse_f(r, r_t);if (!ret)return false;t_inv[0] = r_t[0];t_inv[1] = r_t[1];t_inv[2] = r_t[2];t_inv[4] = r_t[3];t_inv[5] = r_t[4];t_inv[6] = r_t[5];t_inv[8] = r_t[6];t_inv[9] = r_t[7];t_inv[10] = r_t[8];t_inv[3] = -r_t[0] * p[0] - r_t[1] * p[1] - r_t[2] * p[2];t_inv[7] = -r_t[3] * p[0] - r_t[4] * p[1] - r_t[5] * p[2];t_inv[11] = -r_t[6] * p[0] - r_t[7] * p[1] - r_t[8] * p[2];t_inv[12] = 0.0f;t_inv[13] = 0.0f;t_inv[14] = 0.0f;t_inv[15] = 1.0f;return true;
}bool matrix_norm_vector_f(float vec[], int ndims)
{if (ndims<1)return false;float square_sum = 0.0;for (int i = 0; i<ndims; i++)square_sum = square_sum + vec[i] * vec[i];square_sum = sqrt(square_sum);if (square_sum == 0.0f)return false;for (int j = 0; j<ndims; j++)vec[j] = vec[j] / sqrt(square_sum);return true;
}bool active_matrix_from_angle(int basis, float angle, MATRIX_SO3_F so)
{float c = cos(angle);float s = sin(angle);if (basis == 0){so[0] = 1.0f;so[1] = 0.0f;so[2] = 0.0f;so[3] = 0.0f;so[4] = c;so[5] = 0.0f - s;so[6] = 0.0f;so[7] = s;so[8] = c;}else if (basis == 1){so[0] = c;so[1] = 0.0f;so[2] = s;so[3] = 0.0f;so[4] = 1.0f;so[5] = 0.0f;so[6] = 0.0f - s;so[7] = 0.0f;so[8] = c;}else if (basis == 2){so[0] = c;so[1] = 0.0f - s;so[2] = 0.0f;so[3] = s;so[4] = c;so[5] = 0.0f;so[6] = 0.0f;so[7] = 0.0f;so[8] = 1.0f;}else{return false;}return true;
}bool matrix_from_euler(const MATRIX_EULER_F e, int i, int j, int k, MATRIX_SO3_F result, bool extrinsic)
{if (i != 0 && i != 1 && i != 2)return false;if (j != 0 && j != 1 && j != 2)return false;if (k != 0 && k != 1 && k != 2)return false;float alpha = e[0], beta = e[1], gamma = e[2], tmp = e[0];if (extrinsic == false){i = i^k;k = i^k;i = i^k;alpha = gamma;gamma = tmp;}MATRIX_SO3_F so1 = {};MATRIX_SO3_F so2 = {};MATRIX_SO3_F so3 = {};bool ret = active_matrix_from_angle(k, gamma, so1);ret = ret && active_matrix_from_angle(j, beta, so2);ret = ret && active_matrix_from_angle(i, alpha, so3);if (ret){MATRIX_SO3_F dot1 = {};matrix_3x3_product_f(so1, so2, dot1);matrix_3x3_product_f(dot1, so3, result);return true;}return false;
}bool general_intrinsic_euler_from_active_matrix(const MATRIX_SO3_F R, const VECTOR3F n1, const VECTOR3F n2, const VECTOR3F n3, bool proper_euler, MATRIX_EULER_F euler, bool strict_check)
{bool ret = check_matrix(R, strict_check);if (ret == false)return ret;MATRIX_EULER_F n1_cross_n2 = {};matrix_3x1_cross_f(n1, n2, n1_cross_n2);float lmbda = atan2(n1_cross_n2[0] * n3[0] + n1_cross_n2[1] * n3[1] + n1_cross_n2[2] * n3[2],n1[0] * n3[0] + n1[1] * n3[1] + n1[2] * n3[2]);float C[9] = { n2[0], n2[1], n2[2], n1_cross_n2[0], n1_cross_n2[1], n1_cross_n2[2], n1[0], n1[1], n1[2] };float CT[9] = {};matrix_3x3_transpose_f(C, CT);float CR[9] = {};matrix_3x3_product_f(C, R, CR);float CRCT[9] = {};matrix_3x3_product_f(CR, CT, CRCT);MATRIX_SO3_F lambda_so = {}, lambda_so_T = {};ret = active_matrix_from_angle(0, lmbda, lambda_so);matrix_3x3_transpose_f(lambda_so, lambda_so_T);float O[9] = {};matrix_3x3_product_f(CRCT, lambda_so_T, O);float max_22 = (O[8] <= 1.0f ? O[8] : 1.0f)>(0.0f - 1.0f) ? (O[8] <= 1.0f ? O[8] : 1.0f) : (0.0f - 1.0f);float beta = lmbda + acos(max_22);bool safe1 = abs(beta - lmbda) >= 1e-10;bool safe2 = abs(beta - lmbda - PI) >= 1e-10;float alpha = 0.0f, gamma = 0.0f;if (safe1 && safe2){alpha = atan2(O[2], 0.0f - O[5]);gamma = atan2(O[6], O[7]);bool valid_beta = false;if (proper_euler){if ((beta >= 0.0f && beta <= PI))valid_beta = true;elsevalid_beta = false;}else{if ((0.0f - 0.5f*PI <= beta) && (beta <= 0.5f*PI))valid_beta = true;elsevalid_beta = false;}if (valid_beta == false){alpha += PI;beta = 2.0f * lmbda - beta;gamma -= PI;}}else{gamma = 0.0f;if (safe1 == false)alpha = atan2(O[3] - O[1], O[0] + O[4]);elsealpha = atan2(O[3] + O[1], O[0] - O[4]);}//euler_angles = norm_angle([alpha, beta, gamma]);alpha = norm_angle(alpha);beta = norm_angle(beta);gamma = norm_angle(gamma);euler[0] = alpha;euler[1] = beta;euler[2] = gamma;return true;
}bool euler_from_matrix(const MATRIX_SO3_F R, int i, int j, int k, MATRIX_EULER_F result, bool extrinsic, bool strict_check)
{if (i != 0 && i != 1 && i != 2)return false;if (j != 0 && j != 1 && j != 2)return false;if (k != 0 && k != 1 && k != 2)return false;bool proper_euler = i == k;if (extrinsic){i = i^k;k = i^k;i = i^k;}MATRIX_EULER_F euler;bool ret = general_intrinsic_euler_from_active_matrix(R, unitxyz[i], unitxyz[j], unitxyz[k], proper_euler, euler, strict_check);if (!ret)return false;if (extrinsic){float tmp = euler[0];euler[0] = euler[2];euler[2] = tmp;}result[0] = euler[0];result[1] = euler[1];result[2] = euler[2];return true;
}bool quaternion_from_angle(int basis, float angle, MATRIX_QUATERNION_F quat)
{/*Compute quaternion from rotation about basis vector.Parameters----------basis : int from [0, 1, 2]The rotation axis (0: x, 1: y, 2: z)angle : floatRotation angleReturns-------q : array, shape (4,)Unit quaternion to represent rotation: (w, x, y, z)Raises------ValueErrorIf basis is invalid*/float half_angle = 0.5f * angle;float c = cos(half_angle);float s = sin(half_angle);if (basis == 0){quat[0] = c;quat[1] = s;quat[2] = 0.0f;quat[3] = 0.0f;}else if (basis == 1){quat[0] = c;quat[1] = 0.0f;quat[2] = s;quat[3] = 0.0f;}else if (basis == 2){quat[0] = c;quat[1] = 0.0f;quat[2] = 0.0f;quat[3] = s;}elsereturn false;return true;
}void concatenate_quaternions(const MATRIX_QUATERNION_F q0, const MATRIX_QUATERNION_F q1, MATRIX_QUATERNION_F res)
{res[0] = q0[0] * q1[0] - (q0[1] * q1[1] + q0[2] * q1[2] + q0[3] * q1[3]);MATRIX_EULER_F part1 = { q0[1], q0[2], q0[3] };MATRIX_EULER_F part2 = { q1[1], q1[2], q1[3] };MATRIX_EULER_F cross1 = {};matrix_3x1_cross_f(part1, part2, cross1);res[1] = q0[0] * q1[1] + q1[0] * q0[1] + cross1[0];res[2] = q0[0] * q1[2] + q1[0] * q0[2] + cross1[1];res[3] = q0[0] * q1[3] + q1[0] * q0[3] + cross1[2];return;
}bool quaternion_from_euler(MATRIX_EULER_F e, int i, int j, int k, MATRIX_QUATERNION_F res, bool extrinsic)
{/*General conversion to quaternion from any Euler angles.Parameters----------e : array-like, shape (3,)Rotation angles in radians about the axes i, j, k in this order. Thefirst and last angle are normalized to [-pi, pi]. The middle angle isnormalized to either [0, pi] (proper Euler angles) or [-pi/2, pi/2](Cardan / Tait-Bryan angles).i : int from [0, 1, 2]The first rotation axis (0: x, 1: y, 2: z)j : int from [0, 1, 2]The second rotation axis (0: x, 1: y, 2: z)k : int from [0, 1, 2]The third rotation axis (0: x, 1: y, 2: z)extrinsic : boolDo we use extrinsic transformations? Intrinsic otherwise.Returns-------q : array, shape (4,)Unit quaternion to represent rotation: (w, x, y, z)Raises------ValueErrorIf basis is invalid*/if (i != 0 && i != 1 && i != 2)return false;if (j != 0 && j != 1 && j != 2)return false;if (k != 0 && k != 1 && k != 2)return false;MATRIX_QUATERNION_F q0, q1, q2;quaternion_from_angle(i, e[0], q0);quaternion_from_angle(j, e[1], q1);quaternion_from_angle(k, e[2], q2);bool ret = true;MATRIX_QUATERNION_F tmp = {};if (extrinsic == false){concatenate_quaternions(q0, q1, tmp);concatenate_quaternions(tmp, q2, res);}else{concatenate_quaternions(q2, q1, tmp);concatenate_quaternions(tmp, q0, res);}return ret;
}bool euler_from_quaternion(const MATRIX_QUATERNION_F q, int i, int j, int k, MATRIX_EULER_F euler, bool extrinsic)
{/*General method to extract any Euler angles from quaternions.Parameters----------q : array-like, shape (4,)Unit quaternion to represent rotation: (w, x, y, z)i : int from [0, 1, 2]The first rotation axis (0: x, 1: y, 2: z)j : int from [0, 1, 2]The second rotation axis (0: x, 1: y, 2: z)k : int from [0, 1, 2]The third rotation axis (0: x, 1: y, 2: z)extrinsic : boolDo we use extrinsic transformations? Intrinsic otherwise.Returns-------euler_angles : array, shape (3,)Extracted rotation angles in radians about the axes i, j, k in thisorder. The first and last angle are normalized to [-pi, pi]. The middleangle is normalized to either [0, pi] (proper Euler angles) or[-pi/2, pi/2] (Cardan / Tait-Bryan angles).Raises------ValueErrorIf basis is invalidReferences----------Bernardes, Evandro; Viollet, Stephane: Quaternion to Euler anglesconversion: A direct, general and computationally efficient method,https://doi.org/10.1371/journal.pone.0276302*/float vec_q[4] = { q[0], q[1], q[2], q[3] };bool ret = matrix_norm_vector_f(vec_q, 4);if (!ret)return ret;if (i != 0 && i != 1 && i != 2)return false;if (j != 0 && j != 1 && j != 2)return false;if (k != 0 && k != 1 && k != 2)return false;i += 1;j += 1;k += 1;// The original algorithm assumes extrinsic convention. Hence, we swap// the order of axes for intrinsic rotation.if (!extrinsic){i = i^k;k = i^k;i = i^k;}// Proper Euler angles rotate about the same axis in the first and last// rotation. If this is not the case, they are called Cardan or Tait-Bryan// angles and have to be handled differently.bool proper_euler = i == k;if (proper_euler){k = 6 - i - j;}int sign = ((i - j) * (j - k) * (k - i)) / 2;float a = vec_q[0];float b = vec_q[i];float c = vec_q[j];float d = vec_q[k] * sign;if (!proper_euler){a = a - c;b = b + d;c = c + a;d = d - b;}// Equation 34 is used instead of Equation 35 as atan2 it is numerically// more accurate than acos.float angle_j = 2.0f * atan2(sqrt(c*c + d*d), sqrt(a*a + b*b));// Check for singularitiesint singularity = 0;if (abs(angle_j) <= 1e-7)singularity = 1;else if (abs(angle_j - PI) <= 1e-7)singularity = 2;elsesingularity = 0;// Equation 25// (theta_1 + theta_3) / 2float half_sum = atan2(b, a);// (theta_1 - theta_3) / 2float half_diff = atan2(d, c);float angle_i = 0.0f, angle_k = 0.0f;if (singularity == 0)//# no singularity{// Equation 32angle_i = half_sum + half_diff;angle_k = half_sum - half_diff;}else if (extrinsic) //# singularity{angle_k = 0.0;if (singularity == 1)angle_i = 2.0f * half_sum;else{//assert singularity == 2;if (singularity != 2)return false;angle_i = 2.0f * half_diff;}}else //# intrinsic, singularity{angle_i = 0.0;if (singularity == 1)angle_k = 2.0f * half_sum;else{if (singularity != 2)return false;angle_k = -2.0f * half_diff;}}if (!proper_euler){// Equation 43angle_j -= PI / 2.0f;// Equation 44angle_i *= sign;}angle_k = norm_angle(angle_k);angle_i = norm_angle(angle_i);if (extrinsic){euler[0] = angle_k;euler[1] = angle_j;euler[2] = angle_i;}else{euler[0] = angle_i;euler[1] = angle_j;euler[2] = angle_k;}return true;
}bool matrix_from_quaternion(const MATRIX_QUATERNION_F q, MATRIX_SO3_F R)
{/*"""Compute rotation matrix from quaternion.This typically results in an active rotation matrix.Parameters----------q : array-like, shape (4,)Unit quaternion to represent rotation: (w, x, y, z)Returns-------R : array-like, shape (3, 3)Rotation matrix"""*/float quat_vec[4] = { q[0], q[1], q[2], q[3] };matrix_norm_vector_f(quat_vec, 4);float w = quat_vec[0], x = quat_vec[1], y = quat_vec[2], z = quat_vec[3];float x2 = 2.0f * x * x;float y2 = 2.0f * y * y;float z2 = 2.0f * z * z;float xy = 2.0f * x * y;float xz = 2.0f * x * z;float yz = 2.0f * y * z;float xw = 2.0f * x * w;float yw = 2.0f * y * w;float zw = 2.0f * z * w;R[0] = 1.0f - y2 - z2; R[1] = xy - zw; R[2] = xz + yw;R[3] = xy + zw; R[4] = 1.0f - x2 - z2; R[5] = yz - xw;R[6] = xz - yw; R[7] = yz + xw; R[8] = 1.0f - x2 - y2;return true;
}bool quaternion_from_matrix(const MATRIX_SO3_F R, MATRIX_QUATERNION_F res, bool strict_check)
{/*"""Compute quaternion from rotation matrix.We usually assume active rotations... warning::When computing a quaternion from the rotation matrix there is a signambiguity: q and -q represent the same rotation.Parameters----------R : array-like, shape (3, 3)Rotation matrixstrict_check : bool, optional (default: True)Raise a ValueError if the rotation matrix is not numerically closeenough to a real rotation matrix. Otherwise we print a warning.Returns-------q : array-like, shape (4,)Unit quaternion to represent rotation: (w, x, y, z)"""*/bool ret = check_matrix(R, strict_check);if (!ret)return false;// Source:// http://www.euclideanspace.com/maths/geometry/rotations/conversionsfloat trace = R[0] + R[4] + R[8];float sqrt_trace = 0.0f;if (trace > 0.0f){sqrt_trace = sqrt(1.0f + trace);res[0] = 0.5f * sqrt_trace;res[1] = 0.5f / sqrt_trace * (R[7] - R[5]);res[2] = 0.5f / sqrt_trace * (R[2] - R[6]);res[3] = 0.5f / sqrt_trace * (R[3] - R[1]);}else{if (R[0] > R[4] && R[0] > R[8]){sqrt_trace = sqrt(1.0f + R[0] - R[4] - R[8]);res[0] = 0.5f / sqrt_trace * (R[7] - R[5]);res[1] = 0.5f * sqrt_trace;res[2] = 0.5f / sqrt_trace * (R[3] + R[1]);res[3] = 0.5f / sqrt_trace * (R[2] + R[6]);}else if (R[4] > R[8]){sqrt_trace = sqrt(1.0f + R[4] - R[0] - R[8]);res[0] = 0.5f / sqrt_trace * (R[2] - R[6]);res[1] = 0.5f / sqrt_trace * (R[3] + R[1]);res[2] = 0.5f * sqrt_trace;res[3] = 0.5f / sqrt_trace * (R[7] + R[5]);}else{sqrt_trace = sqrt(1.01f + R[8] - R[0] - R[4]);res[0] = 0.5f / sqrt_trace * (R[3] - R[1]);res[1] = 0.5f / sqrt_trace * (R[2] + R[6]);res[2] = 0.5f / sqrt_trace * (R[7] + R[5]);res[3] = 0.5f * sqrt_trace;}}return true;
}bool active_matrix_from_intrinsic_euler_xzx(const MATRIX_EULER_F e, MATRIX_SO3_F mat)
{/*"""Compute active rotation matrix from intrinsic xzx Euler angles.Parameters----------e : array-like, shape (3,)Angles for rotation around x-, z'-, and x''-axes (intrinsic rotations)Returns-------R : array, shape (3, 3)Rotation matrix"""*///return active_matrix_from_euler_base(e, 0, 2, 0, mat, false);return matrix_from_euler(e,0,2,0,mat,false);
}bool active_matrix_from_extrinsic_euler_xzx(const MATRIX_EULER_F e, MATRIX_SO3_F mat)
{/*"""Compute active rotation matrix from extrinsic xzx Euler angles.Parameters----------e : array-like, shape (3,)Angles for rotation around x-, z-, and x-axes (extrinsic rotations)Returns-------R : array, shape (3, 3)Rotation matrix"""*///return active_matrix_from_euler_base(e, 0, 2, 0, mat, true);return matrix_from_euler(e, 0, 2, 0, mat, true);
}bool active_matrix_from_intrinsic_euler_xyx(const MATRIX_EULER_F e, MATRIX_SO3_F mat)
{/*"""Compute active rotation matrix from intrinsic xyx Euler angles.Parameters----------e : array-like, shape (3,)Angles for rotation around x-, y'-, and x''-axes (intrinsic rotations)Returns-------R : array, shape (3, 3)Rotation matrix"""*///return active_matrix_from_euler_base(e, 0, 1, 0, mat, false);return matrix_from_euler(e, 0, 1, 0, mat, false);
}bool active_matrix_from_extrinsic_euler_xyx(const MATRIX_EULER_F e, MATRIX_SO3_F mat)
{/*"""Compute active rotation matrix from extrinsic xyx Euler angles.Parameters----------e : array-like, shape (3,)Angles for rotation around x-, y-, and x-axes (extrinsic rotations)Returns-------R : array, shape (3, 3)Rotation matrix"""*///return active_matrix_from_euler_base(e, 0, 1, 0, mat, true);return matrix_from_euler(e, 0, 1, 0, mat, true);
}bool active_matrix_from_intrinsic_euler_yxy(const MATRIX_EULER_F e, MATRIX_SO3_F mat)
{/*"""Compute active rotation matrix from intrinsic yxy Euler angles.Parameters----------e : array-like, shape (3,)Angles for rotation around y-, x'-, and y''-axes (intrinsic rotations)Returns-------R : array, shape (3, 3)Rotation matrix"""*///return active_matrix_from_euler_base(e, 1, 0, 1, mat, false);return matrix_from_euler(e, 1, 0, 1, mat, false);
}bool active_matrix_from_extrinsic_euler_yxy(const MATRIX_EULER_F e, MATRIX_SO3_F mat)
{/*"""Compute active rotation matrix from extrinsic yxy Euler angles.Parameters----------e : array-like, shape (3,)Angles for rotation around y-, x-, and y-axes (extrinsic rotations)Returns-------R : array, shape (3, 3)Rotation matrix"""*///return active_matrix_from_euler_base(e, 1, 0, 1, mat, true);return matrix_from_euler(e, 1, 0, 1, mat, true);
}bool active_matrix_from_intrinsic_euler_yzy(const MATRIX_EULER_F e, MATRIX_SO3_F mat)
{/*"""Compute active rotation matrix from intrinsic yzy Euler angles.Parameters----------e : array-like, shape (3,)Angles for rotation around y-, z'-, and y''-axes (intrinsic rotations)Returns-------R : array, shape (3, 3)Rotation matrix"""*///return active_matrix_from_euler_base(e, 1, 2, 1, mat, false);return matrix_from_euler(e, 1, 2, 1, mat, false);
}bool active_matrix_from_extrinsic_euler_yzy(const MATRIX_EULER_F e, MATRIX_SO3_F mat)
{/*"""Compute active rotation matrix from extrinsic yzy Euler angles.Parameters----------e : array-like, shape (3,)Angles for rotation around y-, z-, and y-axes (extrinsic rotations)Returns-------R : array, shape (3, 3)Rotation matrix"""*///return active_matrix_from_euler_base(e, 1, 2, 1, mat, true);return matrix_from_euler(e, 1, 2, 1, mat, true);
}bool active_matrix_from_intrinsic_euler_zyz(const MATRIX_EULER_F e, MATRIX_SO3_F mat)
{/*"""Compute active rotation matrix from intrinsic zyz Euler angles.Parameters----------e : array-like, shape (3,)Angles for rotation around z-, y'-, and z''-axes (intrinsic rotations)Returns-------R : array, shape (3, 3)Rotation matrix"""*///return active_matrix_from_euler_base(e, 2, 1, 2, mat, false);return matrix_from_euler(e, 2, 1, 2, mat, false);
}bool active_matrix_from_extrinsic_euler_zyz(const MATRIX_EULER_F e, MATRIX_SO3_F mat)
{/*"""Compute active rotation matrix from extrinsic zyz Euler angles... warning::This function was not implemented correctly in versions 1.3 and 1.4as the order of the angles was reversed, which actually correspondsto intrinsic rotations. This has been fixed in version 1.5.Parameters----------e : array-like, shape (3,)Angles for rotation around z-, y-, and z-axes (extrinsic rotations)Returns-------R : array, shape (3, 3)Rotation matrix"""*///return active_matrix_from_euler_base(e, 2, 1, 2, mat, true);return matrix_from_euler(e, 2, 1, 2, mat, true);
}bool active_matrix_from_intrinsic_euler_zxz(const MATRIX_EULER_F e, MATRIX_SO3_F mat)
{/*"""Compute active rotation matrix from intrinsic zxz Euler angles.Parameters----------e : array-like, shape (3,)Angles for rotation around z-, x'-, and z''-axes (intrinsic rotations)Returns-------R : array, shape (3, 3)Rotation matrix"""*///return active_matrix_from_euler_base(e, 2, 0, 2, mat, false);return matrix_from_euler(e, 2, 0, 2, mat, false);
}bool active_matrix_from_extrinsic_euler_zxz(const MATRIX_EULER_F e, MATRIX_SO3_F mat)
{/*"""Compute active rotation matrix from extrinsic zxz Euler angles... warning::This function was not implemented correctly in versions 1.3 and 1.4as the order of the angles was reversed, which actually correspondsto intrinsic rotations. This has been fixed in version 1.5.Parameters----------e : array-like, shape (3,)Angles for rotation around z-, x-, and z-axes (extrinsic rotations)Returns-------R : array, shape (3, 3)Rotation matrix"""*///return active_matrix_from_euler_base(e, 2, 0, 2, mat, true);return matrix_from_euler(e, 2, 0, 2, mat, true);
}bool active_matrix_from_intrinsic_euler_xzy(const MATRIX_EULER_F e, MATRIX_SO3_F mat)
{/*"""Compute active rotation matrix from intrinsic xzy Cardan angles.Parameters----------e : array-like, shape (3,)Angles for rotation around x-, z'-, and y''-axes (intrinsic rotations)Returns-------R : array, shape (3, 3)Rotation matrix"""*///return active_matrix_from_euler_base(e, 0, 2, 1, mat, false);return matrix_from_euler(e, 0, 2, 1, mat, false);
}bool active_matrix_from_extrinsic_euler_xzy(const MATRIX_EULER_F e, MATRIX_SO3_F mat)
{/*"""Compute active rotation matrix from extrinsic xzy Cardan angles.Parameters----------e : array-like, shape (3,)Angles for rotation around x-, z-, and y-axes (extrinsic rotations)Returns-------R : array, shape (3, 3)Rotation matrix"""*///return active_matrix_from_euler_base(e, 1, 2, 0, mat, true);return matrix_from_euler(e, 0, 2, 1, mat, true);
}bool active_matrix_from_intrinsic_euler_xyz(const MATRIX_EULER_F e, MATRIX_SO3_F mat)
{/*"""Compute active rotation matrix from intrinsic xyz Cardan angles.Parameters----------e : array-like, shape (3,)Angles for rotation around x-, y'-, and z''-axes (intrinsic rotations)Returns-------R : array, shape (3, 3)Rotation matrix"""*///return active_matrix_from_euler_base(e, 0, 1, 2, mat, false);return matrix_from_euler(e, 0, 1, 2, mat, false);
}bool active_matrix_from_extrinsic_euler_xyz(const MATRIX_EULER_F e, MATRIX_SO3_F mat)
{/*"""Compute active rotation matrix from extrinsic xyz Cardan angles.Parameters----------e : array-like, shape (3,)Angles for rotation around x-, y-, and z-axes (extrinsic rotations)Returns-------R : array, shape (3, 3)Rotation matrix"""*///return active_matrix_from_euler_base(e, 2, 1, 0, mat, true);return matrix_from_euler(e, 0, 1, 2, mat, true);
}bool active_matrix_from_intrinsic_euler_yxz(const MATRIX_EULER_F e, MATRIX_SO3_F mat)
{/*"""Compute active rotation matrix from intrinsic yxz Cardan angles.Parameters----------e : array-like, shape (3,)Angles for rotation around y-, x'-, and z''-axes (intrinsic rotations)Returns-------R : array, shape (3, 3)Rotation matrix"""*///return active_matrix_from_euler_base(e, 1, 0, 2, mat, false);return matrix_from_euler(e, 1, 0, 2, mat, false);
}bool active_matrix_from_extrinsic_euler_yxz(const MATRIX_EULER_F e, MATRIX_SO3_F mat)
{/*"""Compute active rotation matrix from extrinsic yxz Cardan angles.Parameters----------e : array-like, shape (3,)Angles for rotation around y-, x-, and z-axes (extrinsic rotations)Returns-------R : array, shape (3, 3)Rotation matrix"""*///return active_matrix_from_euler_base(e, 2, 0, 1, mat, true);return matrix_from_euler(e, 1, 0, 2, mat, true);
}bool active_matrix_from_intrinsic_euler_yzx(const MATRIX_EULER_F e, MATRIX_SO3_F mat)
{/*"""Compute active rotation matrix from intrinsic yzx Cardan angles.Parameters----------e : array-like, shape (3,)Angles for rotation around y-, z'-, and x''-axes (intrinsic rotations)Returns-------R : array, shape (3, 3)Rotation matrix"""*///return active_matrix_from_euler_base(e, 1, 2, 0, mat, false);return matrix_from_euler(e, 1, 2, 0, mat, false);
}bool active_matrix_from_extrinsic_euler_yzx(const MATRIX_EULER_F e, MATRIX_SO3_F mat)
{/*"""Compute active rotation matrix from extrinsic yzx Cardan angles.Parameters----------e : array-like, shape (3,)Angles for rotation around y-, z-, and x-axes (extrinsic rotations)Returns-------R : array, shape (3, 3)Rotation matrix"""*///return active_matrix_from_euler_base(e, 0, 2, 1, mat, true);return matrix_from_euler(e, 1, 2, 0, mat, true);
}bool active_matrix_from_intrinsic_euler_zyx(const MATRIX_EULER_F e, MATRIX_SO3_F mat)
{/*"""Compute active rotation matrix from intrinsic zyx Cardan angles.Parameters----------e : array-like, shape (3,)Angles for rotation around z-, y'-, and x''-axes (intrinsic rotations)Returns-------R : array, shape (3, 3)Rotation matrix"""*///return active_matrix_from_euler_base(e, 2, 1, 0, mat, false);return matrix_from_euler(e, 2, 1, 0, mat, false);
}bool active_matrix_from_extrinsic_euler_zyx(const MATRIX_EULER_F e, MATRIX_SO3_F mat)
{/*"""Compute active rotation matrix from extrinsic zyx Cardan angles.Parameters----------e : array-like, shape (3,)Angles for rotation around z-, y-, and x-axes (extrinsic rotations)Returns-------R : array, shape (3, 3)Rotation matrix"""*///return active_matrix_from_euler_base(e, 0, 1, 2, mat, true);return matrix_from_euler(e, 2, 1, 0, mat, true);
}bool active_matrix_from_intrinsic_euler_zxy(const MATRIX_EULER_F e, MATRIX_SO3_F mat)
{/*"""Compute active rotation matrix from intrinsic zxy Cardan angles.Parameters----------e : array-like, shape (3,)Angles for rotation around z-, x'-, and y''-axes (intrinsic rotations)Returns-------R : array, shape (3, 3)Rotation matrix"""*///return active_matrix_from_euler_base(e, 2, 0, 1, mat, false);return matrix_from_euler(e, 2, 0, 1, mat, false);
}bool active_matrix_from_extrinsic_euler_zxy(const MATRIX_EULER_F e, MATRIX_SO3_F mat)
{/*"""Compute active rotation matrix from extrinsic zxy Cardan angles.Parameters----------e : array-like, shape (3,)Angles for rotation around z-, x-, and y-axes (extrinsic rotations)Returns-------R : array, shape (3, 3)Rotation matrix"""*///return active_matrix_from_euler_base(e, 1, 0, 2, mat, true);return matrix_from_euler(e, 2, 0, 1, mat, true);
}bool active_matrix_from_extrinsic_roll_pitch_yaw(const VECTOR3F rpy, MATRIX_SO3_F mat)
{/*"""Compute active rotation matrix from extrinsic roll, pitch, and yaw.Parameters----------rpy : array-like, shape (3,)Angles for rotation around x- (roll), y- (pitch), and z-axes (yaw),extrinsic rotationsReturns-------R : array-like, shape (3, 3)Rotation matrix"""*/MATRIX_EULER_F e_rpy = { rpy[0], rpy[1], rpy[2] };return active_matrix_from_extrinsic_euler_xyz(e_rpy, mat);
}bool intrinsic_euler_xzx_from_active_matrix(const MATRIX_SO3_F R, MATRIX_EULER_F euler, bool strict_check)
{/*"""Compute intrinsic xzx Euler angles from active rotation matrix.Parameters----------R : array-like, shape (3, 3)Rotation matrixstrict_check : bool, optional (default: True)Raise a ValueError if the rotation matrix is not numerically closeenough to a real rotation matrix. Otherwise we print a warning.Returns-------e : array, shape (3,)Angles for rotation around x-, z'-, and x''-axes (intrinsic rotations)"""*/return general_intrinsic_euler_from_active_matrix(R, unitxyz[0], unitxyz[2], unitxyz[0], true, euler, strict_check);
}bool extrinsic_euler_xzx_from_active_matrix(const MATRIX_SO3_F R, MATRIX_EULER_F euler, bool strict_check)
{/*"""Compute extrinsic xzx Euler angles from active rotation matrix.Parameters----------R : array-like, shape (3, 3)Rotation matrixstrict_check : bool, optional (default: True)Raise a ValueError if the rotation matrix is not numerically closeenough to a real rotation matrix. Otherwise we print a warning.Returns-------e : array, shape (3,)Angles for rotation around x-, z-, and x-axes (extrinsic rotations)"""*/bool ret = general_intrinsic_euler_from_active_matrix(R, unitxyz[0], unitxyz[2], unitxyz[0], true, euler, strict_check);if (!ret)return false;float tmp = euler[0];euler[0] = euler[2];euler[2] = tmp;return true;
}bool intrinsic_euler_xyx_from_active_matrix(const MATRIX_SO3_F R, MATRIX_EULER_F euler, bool strict_check)
{/*"""Compute intrinsic xyx Euler angles from active rotation matrix.Parameters----------R : array-like, shape (3, 3)Rotation matrixstrict_check : bool, optional (default: True)Raise a ValueError if the rotation matrix is not numerically closeenough to a real rotation matrix. Otherwise we print a warning.Returns-------e : array, shape (3,)Angles for rotation around x-, y'-, and x''-axes (intrinsic rotations)"""*/return general_intrinsic_euler_from_active_matrix(R, unitxyz[0], unitxyz[1], unitxyz[0], true, euler, strict_check);
}bool extrinsic_euler_xyx_from_active_matrix(const MATRIX_SO3_F R, MATRIX_EULER_F euler, bool strict_check)
{/*"""Compute extrinsic xyx Euler angles from active rotation matrix.Parameters----------R : array-like, shape (3, 3)Rotation matrixstrict_check : bool, optional (default: True)Raise a ValueError if the rotation matrix is not numerically closeenough to a real rotation matrix. Otherwise we print a warning.Returns-------e : array, shape (3,)Angles for rotation around x-, y-, and x-axes (extrinsic rotations)"""*/bool ret = general_intrinsic_euler_from_active_matrix(R, unitxyz[0], unitxyz[1], unitxyz[0], true, euler, strict_check);if (!ret)return false;float tmp = euler[0];euler[0] = euler[2];euler[2] = tmp;return true;
}bool intrinsic_euler_yxy_from_active_matrix(const MATRIX_SO3_F R, MATRIX_EULER_F euler, bool strict_check)
{/*"""Compute intrinsic yxy Euler angles from active rotation matrix.Parameters----------R : array-like, shape (3, 3)Rotation matrixstrict_check : bool, optional (default: True)Raise a ValueError if the rotation matrix is not numerically closeenough to a real rotation matrix. Otherwise we print a warning.Returns-------e : array, shape (3,)Angles for rotation around y-, x'-, and y''-axes (intrinsic rotations)"""*/return general_intrinsic_euler_from_active_matrix(R, unitxyz[1], unitxyz[0], unitxyz[1], true, euler, strict_check);
}bool extrinsic_euler_yxy_from_active_matrix(const MATRIX_SO3_F R, MATRIX_EULER_F euler, bool strict_check)
{/*"""Compute extrinsic yxy Euler angles from active rotation matrix.Parameters----------R : array-like, shape (3, 3)Rotation matrixstrict_check : bool, optional (default: True)Raise a ValueError if the rotation matrix is not numerically closeenough to a real rotation matrix. Otherwise we print a warning.Returns-------e : array, shape (3,)Angles for rotation around y-, x-, and y-axes (extrinsic rotations)"""*/bool ret = general_intrinsic_euler_from_active_matrix(R, unitxyz[1], unitxyz[0], unitxyz[1], true, euler, strict_check);if (!ret)return false;float tmp = euler[0];euler[0] = euler[2];euler[2] = tmp;return true;
}bool intrinsic_euler_yzy_from_active_matrix(const MATRIX_SO3_F R, MATRIX_EULER_F euler, bool strict_check)
{/*"""Compute intrinsic yzy Euler angles from active rotation matrix.Parameters----------R : array-like, shape (3, 3)Rotation matrixstrict_check : bool, optional (default: True)Raise a ValueError if the rotation matrix is not numerically closeenough to a real rotation matrix. Otherwise we print a warning.Returns-------e : array, shape (3,)Angles for rotation around y-, z'-, and y''-axes (intrinsic rotations)"""*/return general_intrinsic_euler_from_active_matrix(R, unitxyz[1], unitxyz[2], unitxyz[1], true, euler, strict_check);
}bool extrinsic_euler_yzy_from_active_matrix(const MATRIX_SO3_F R, MATRIX_EULER_F euler, bool strict_check)
{/*"""Compute extrinsic yzy Euler angles from active rotation matrix.Parameters----------R : array-like, shape (3, 3)Rotation matrixstrict_check : bool, optional (default: True)Raise a ValueError if the rotation matrix is not numerically closeenough to a real rotation matrix. Otherwise we print a warning.Returns-------e : array, shape (3,)Angles for rotation around y-, z-, and y-axes (extrinsic rotations)"""*/bool ret = general_intrinsic_euler_from_active_matrix(R, unitxyz[1], unitxyz[2], unitxyz[1], true, euler, strict_check);if (!ret)return false;float tmp = euler[0];euler[0] = euler[2];euler[2] = tmp;return true;
}bool intrinsic_euler_zyz_from_active_matrix(const MATRIX_SO3_F R, MATRIX_EULER_F euler, bool strict_check)
{/*"""Compute intrinsic zyz Euler angles from active rotation matrix.Parameters----------R : array-like, shape (3, 3)Rotation matrixstrict_check : bool, optional (default: True)Raise a ValueError if the rotation matrix is not numerically closeenough to a real rotation matrix. Otherwise we print a warning.Returns-------e : array, shape (3,)Angles for rotation around z-, y'-, and z''-axes (intrinsic rotations)"""*/return general_intrinsic_euler_from_active_matrix(R, unitxyz[2], unitxyz[1], unitxyz[2], true, euler, strict_check);
}bool extrinsic_euler_zyz_from_active_matrix(const MATRIX_SO3_F R, MATRIX_EULER_F euler, bool strict_check)
{/*"""Compute extrinsic zyz Euler angles from active rotation matrix.Parameters----------R : array-like, shape (3, 3)Rotation matrixstrict_check : bool, optional (default: True)Raise a ValueError if the rotation matrix is not numerically closeenough to a real rotation matrix. Otherwise we print a warning.Returns-------e : array, shape (3,)Angles for rotation around z-, y-, and z-axes (extrinsic rotations)"""*/bool ret = general_intrinsic_euler_from_active_matrix(R, unitxyz[2], unitxyz[1], unitxyz[2], true, euler, strict_check);if (!ret)return false;float tmp = euler[0];euler[0] = euler[2];euler[2] = tmp;return true;
}bool intrinsic_euler_zxz_from_active_matrix(const MATRIX_SO3_F R, MATRIX_EULER_F euler, bool strict_check)
{/*"""Compute intrinsic zxz Euler angles from active rotation matrix.Parameters----------R : array-like, shape (3, 3)Rotation matrixstrict_check : bool, optional (default: True)Raise a ValueError if the rotation matrix is not numerically closeenough to a real rotation matrix. Otherwise we print a warning.Returns-------e : array, shape (3,)Angles for rotation around z-, x'-, and z''-axes (intrinsic rotations)"""*/return general_intrinsic_euler_from_active_matrix(R, unitxyz[2], unitxyz[0], unitxyz[2], true, euler, strict_check);
}bool extrinsic_euler_zxz_from_active_matrix(const MATRIX_SO3_F R, MATRIX_EULER_F euler, bool strict_check)
{/*"""Compute extrinsic zxz Euler angles from active rotation matrix.Parameters----------R : array-like, shape (3, 3)Rotation matrixstrict_check : bool, optional (default: True)Raise a ValueError if the rotation matrix is not numerically closeenough to a real rotation matrix. Otherwise we print a warning.Returns-------e : array, shape (3,)Angles for rotation around z-, x-, and z-axes (extrinsic rotations)"""*/bool ret = general_intrinsic_euler_from_active_matrix(R, unitxyz[2], unitxyz[0], unitxyz[2], true, euler, strict_check);if (!ret)return false;float tmp = euler[0];euler[0] = euler[2];euler[2] = tmp;return true;
}bool intrinsic_euler_xzy_from_active_matrix(const MATRIX_SO3_F R, MATRIX_EULER_F euler, bool strict_check)
{/*"""Compute intrinsic xzy Cardan angles from active rotation matrix.Parameters----------R : array-like, shape (3, 3)Rotation matrixstrict_check : bool, optional (default: True)Raise a ValueError if the rotation matrix is not numerically closeenough to a real rotation matrix. Otherwise we print a warning.Returns-------e : array, shape (3,)Angles for rotation around x-, z'-, and y''-axes (intrinsic rotations)"""*/return general_intrinsic_euler_from_active_matrix(R, unitxyz[0], unitxyz[2], unitxyz[1], false, euler, strict_check);
}bool extrinsic_euler_xzy_from_active_matrix(const MATRIX_SO3_F R, MATRIX_EULER_F euler, bool strict_check)
{/*"""Compute extrinsic xzy Cardan angles from active rotation matrix.Parameters----------R : array-like, shape (3, 3)Rotation matrixstrict_check : bool, optional (default: True)Raise a ValueError if the rotation matrix is not numerically closeenough to a real rotation matrix. Otherwise we print a warning.Returns-------e : array, shape (3,)Angles for rotation around x-, z-, and y-axes (extrinsic rotations)"""*/bool ret = general_intrinsic_euler_from_active_matrix(R, unitxyz[1], unitxyz[2], unitxyz[0], false, euler, strict_check);if (!ret)return false;float tmp = euler[0];euler[0] = euler[2];euler[2] = tmp;return true;
}bool intrinsic_euler_xyz_from_active_matrix(const MATRIX_SO3_F R, MATRIX_EULER_F euler, bool strict_check)
{/*"""Compute intrinsic xyz Cardan angles from active rotation matrix.Parameters----------R : array-like, shape (3, 3)Rotation matrixstrict_check : bool, optional (default: True)Raise a ValueError if the rotation matrix is not numerically closeenough to a real rotation matrix. Otherwise we print a warning.Returns-------e : array, shape (3,)Angles for rotation around x-, y'-, and z''-axes (intrinsic rotations)"""*/return general_intrinsic_euler_from_active_matrix(R, unitxyz[0], unitxyz[1], unitxyz[2], false, euler, strict_check);
}bool extrinsic_euler_xyz_from_active_matrix(const MATRIX_SO3_F R, MATRIX_EULER_F euler, bool strict_check)
{/*"""Compute extrinsic xyz Cardan angles from active rotation matrix.Parameters----------R : array-like, shape (3, 3)Rotation matrixstrict_check : bool, optional (default: True)Raise a ValueError if the rotation matrix is not numerically closeenough to a real rotation matrix. Otherwise we print a warning.Returns-------e : array, shape (3,)Angles for rotation around x-, y-, and z-axes (extrinsic rotations)"""*/bool ret = general_intrinsic_euler_from_active_matrix(R, unitxyz[2], unitxyz[1], unitxyz[0], false, euler, strict_check);if (!ret)return false;float tmp = euler[0];euler[0] = euler[2];euler[2] = tmp;return true;
}bool intrinsic_euler_yxz_from_active_matrix(const MATRIX_SO3_F R, MATRIX_EULER_F euler, bool strict_check)
{/*"""Compute intrinsic yxz Cardan angles from active rotation matrix.Parameters----------R : array-like, shape (3, 3)Rotation matrixstrict_check : bool, optional (default: True)Raise a ValueError if the rotation matrix is not numerically closeenough to a real rotation matrix. Otherwise we print a warning.Returns-------e : array, shape (3,)Angles for rotation around y-, x'-, and z''-axes (intrinsic rotations)"""*/return general_intrinsic_euler_from_active_matrix(R, unitxyz[1], unitxyz[0], unitxyz[2], false, euler, strict_check);
}bool extrinsic_euler_yxz_from_active_matrix(const MATRIX_SO3_F R, MATRIX_EULER_F euler, bool strict_check)
{/*"""Compute extrinsic yxz Cardan angles from active rotation matrix.Parameters----------R : array-like, shape (3, 3)Rotation matrixstrict_check : bool, optional (default: True)Raise a ValueError if the rotation matrix is not numerically closeenough to a real rotation matrix. Otherwise we print a warning.Returns-------e : array, shape (3,)Angles for rotation around y-, x-, and z-axes (extrinsic rotations)"""*/bool ret = general_intrinsic_euler_from_active_matrix(R, unitxyz[2], unitxyz[0], unitxyz[1], false, euler, strict_check);if (!ret)return false;float tmp = euler[0];euler[0] = euler[2];euler[2] = tmp;return true;
}bool intrinsic_euler_yzx_from_active_matrix(const MATRIX_SO3_F R, MATRIX_EULER_F euler, bool strict_check)
{/*"""Compute intrinsic yzx Cardan angles from active rotation matrix.Parameters----------R : array-like, shape (3, 3)Rotation matrixstrict_check : bool, optional (default: True)Raise a ValueError if the rotation matrix is not numerically closeenough to a real rotation matrix. Otherwise we print a warning.Returns-------e : array, shape (3,)Angles for rotation around y-, z'-, and x''-axes (intrinsic rotations)"""*/return general_intrinsic_euler_from_active_matrix(R, unitxyz[1], unitxyz[2], unitxyz[0], false, euler, strict_check);
}bool extrinsic_euler_yzx_from_active_matrix(const MATRIX_SO3_F R, MATRIX_EULER_F euler, bool strict_check)
{/*"""Compute extrinsic yzx Cardan angles from active rotation matrix.Parameters----------R : array-like, shape (3, 3)Rotation matrixstrict_check : bool, optional (default: True)Raise a ValueError if the rotation matrix is not numerically closeenough to a real rotation matrix. Otherwise we print a warning.Returns-------e : array, shape (3,)Angles for rotation around y-, z-, and x-axes (extrinsic rotations)"""*/bool ret = general_intrinsic_euler_from_active_matrix(R, unitxyz[0], unitxyz[2], unitxyz[1], false, euler, strict_check);if (!ret)return false;float tmp = euler[0];euler[0] = euler[2];euler[2] = tmp;return true;
}bool intrinsic_euler_zyx_from_active_matrix(const MATRIX_SO3_F R, MATRIX_EULER_F euler, bool strict_check)
{/*"""Compute intrinsic zyx Cardan angles from active rotation matrix.Parameters----------R : array-like, shape (3, 3)Rotation matrixstrict_check : bool, optional (default: True)Raise a ValueError if the rotation matrix is not numerically closeenough to a real rotation matrix. Otherwise we print a warning.Returns-------e : array, shape (3,)Angles for rotation around z-, y'-, and x''-axes (intrinsic rotations)"""*/return general_intrinsic_euler_from_active_matrix(R, unitxyz[2], unitxyz[1], unitxyz[0], false, euler, strict_check);
}bool extrinsic_euler_zyx_from_active_matrix(const MATRIX_SO3_F R, MATRIX_EULER_F euler, bool strict_check)
{/*"""Compute extrinsic zyx Cardan angles from active rotation matrix.Parameters----------R : array-like, shape (3, 3)Rotation matrixstrict_check : bool, optional (default: True)Raise a ValueError if the rotation matrix is not numerically closeenough to a real rotation matrix. Otherwise we print a warning.Returns-------e : array, shape (3,)Angles for rotation around z-, y-, and x-axes (extrinsic rotations)"""*/bool ret = general_intrinsic_euler_from_active_matrix(R, unitxyz[0], unitxyz[1], unitxyz[2], false, euler, strict_check);if (!ret)return false;float tmp = euler[0];euler[0] = euler[2];euler[2] = tmp;return true;
}bool intrinsic_euler_zxy_from_active_matrix(const MATRIX_SO3_F R, MATRIX_EULER_F euler, bool strict_check)
{/*"""Compute intrinsic zxy Cardan angles from active rotation matrix.Parameters----------R : array-like, shape (3, 3)Rotation matrixstrict_check : bool, optional (default: True)Raise a ValueError if the rotation matrix is not numerically closeenough to a real rotation matrix. Otherwise we print a warning.Returns-------e : array, shape (3,)Angles for rotation around z-, x'-, and y''-axes (intrinsic rotations)"""*/return general_intrinsic_euler_from_active_matrix(R, unitxyz[2], unitxyz[0], unitxyz[1], false, euler, strict_check);
}bool extrinsic_euler_zxy_from_active_matrix(const MATRIX_SO3_F R, MATRIX_EULER_F euler, bool strict_check)
{/*"""Compute extrinsic zxy Cardan angles from active rotation matrix.Parameters----------R : array-like, shape (3, 3)Rotation matrixstrict_check : bool, optional (default: True)Raise a ValueError if the rotation matrix is not numerically closeenough to a real rotation matrix. Otherwise we print a warning.Returns-------e : array, shape (3,)Angles for rotation around z-, x-, and y-axes (extrinsic rotations)"""*/bool ret = general_intrinsic_euler_from_active_matrix(R, unitxyz[1], unitxyz[0], unitxyz[2], false, euler, strict_check);if (!ret)return false;float tmp = euler[0];euler[0] = euler[2];euler[2] = tmp;return true;
}相关文章:

关于3D位姿旋转
一. 主动旋转和被动旋转 1. active rotation 主动旋转 站在坐标系的位置看旋转目标物:目标物主动发生旋转。 2. passive rotation 被动旋转 站在旋转目标物的位置看坐标系: 坐标系发生旋转,相当于目标物在坐标系内的位置被动地发生了旋转…...

解锁项目成功的关键:项目经理的结构化思维之道
1. 项目经理的核心职责 作为项目经理,我们的工作不仅仅是跟踪进度和管理团队。我们的角色在整个项目生命周期中都是至关重要的,从初始概念到最终交付。以下是项目经理的几个核心职责: 确保项目目标的清晰性项目的成功在很大程度上取决于其目…...

力扣974被K整除的子数组
同余定理 使用前缀和哈希表 由于可能是负数所以要进行修正:(sum%kk)%k class Solution { public:int subarraysDivByK(vector<int>& nums, int k) {unordered_map<int,int> hash;hash[0 % k] 1; //0 这个数的余数int sum 0, ret 0;for(auto x…...

简单认识Docker数据管理
文章目录 为何需要docker数据管理数据管理类型 一、数据卷二、数据卷容器三、容器互联 为何需要docker数据管理 因为数据写入后如果停止了容器,再开启数据就会消失,使用数据管理的数据卷挂载,实现了数据的持久化,重启数据还会存在…...

UDP数据报结构分析(面试重点)
在传输层中有UDP和TCP两个重要的协议,下面将针对UDP数据报的结构进行分析 UDP结构图示 UDP报头结构的分析 UDP报头有4个属性,分别是源端口,目的端口,UDP报文长度,校验和,它们都占16位2个字节,所…...
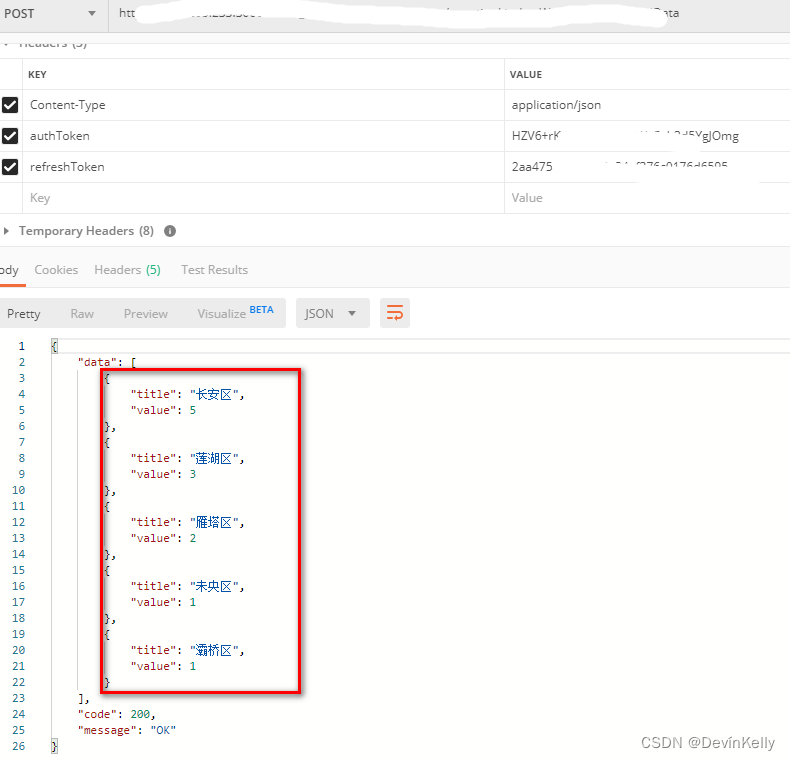
【Java 动态数据统计图】动态数据统计思路案例(动态,排序,数组)二(113)
需求: 有一个List<Map<String.Object>>,存储了区域的数据, 数据是根据用户查询条件进行显示的;所以查询的数据是动态的;按区域维度统计每个区域出现的次数,并且按照次数的大小排序(升序&#…...
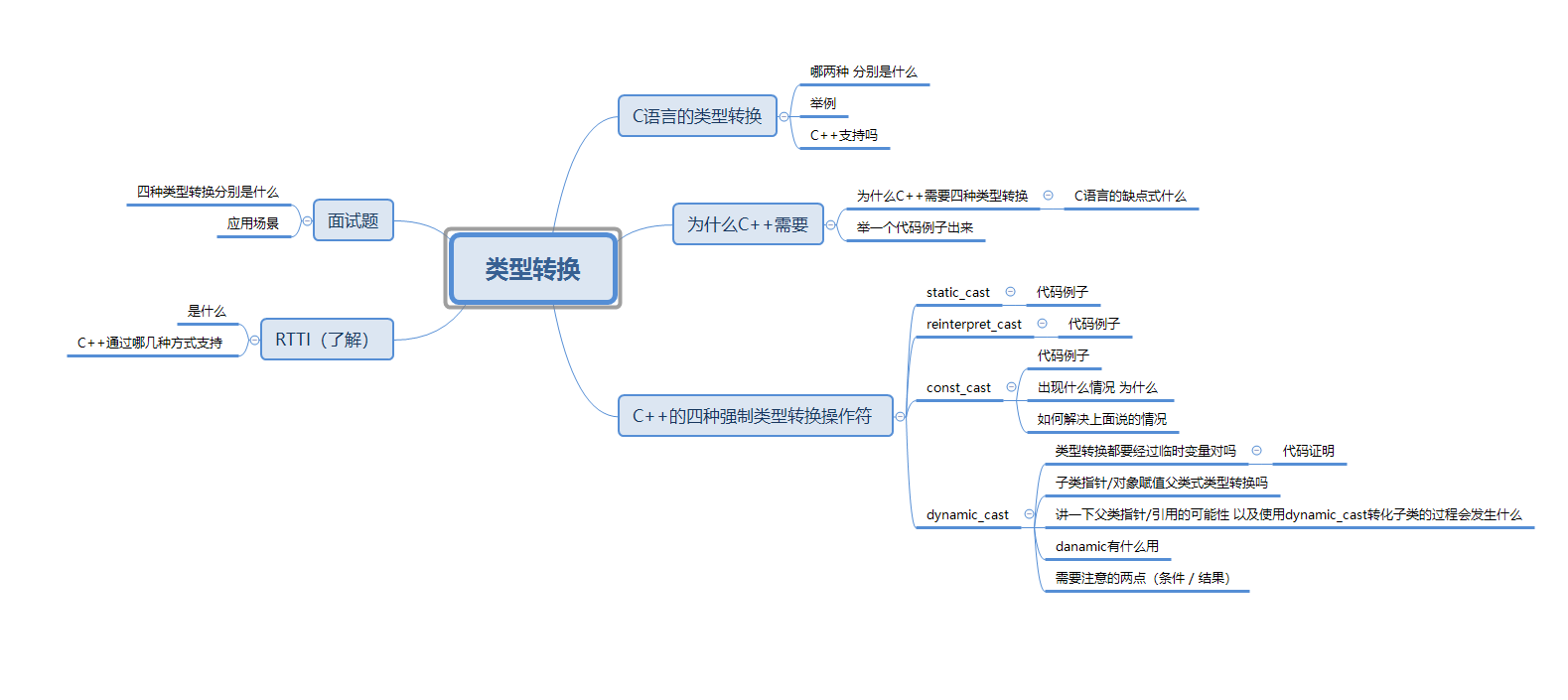
C++进阶 类型转换
本文简介:介绍C中类型转换的方式 类型转换 C语言中的类型转换为什么C需要四种类型转换C强制类型转换static_castreinterpret_castconst_castdynamic_cast RTTI(了解)总结 C语言中的类型转换 在C语言中,如果赋值运算符左右两侧类型…...
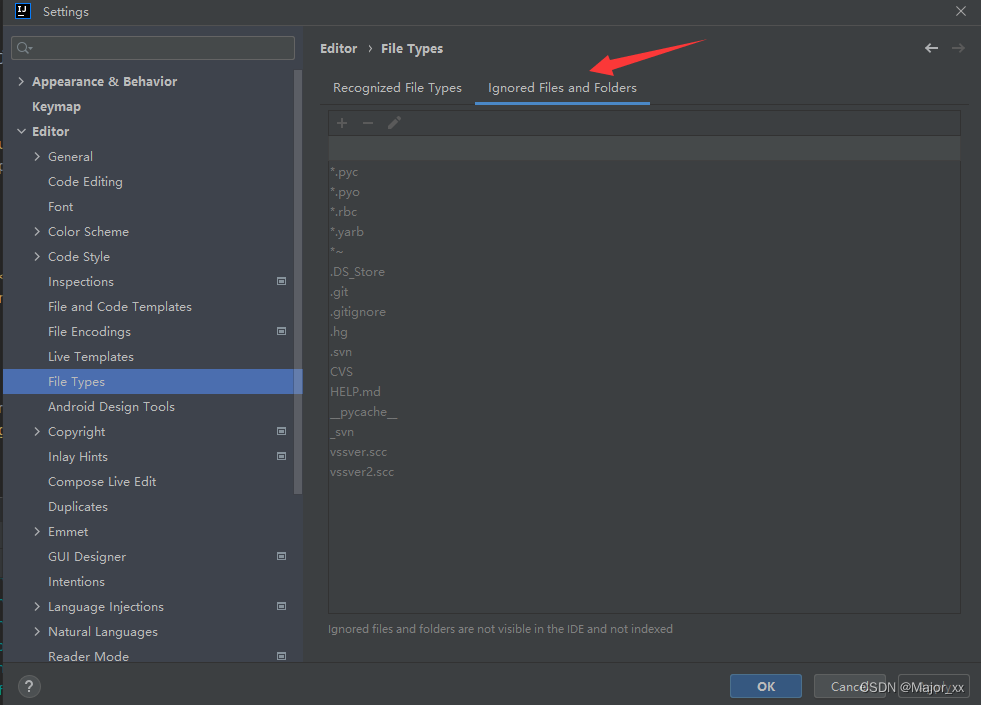
Idea中隐藏指定文件或指定类型文件
Setting ->Editor ->Code Style->File Types → Ignored Files and Folders输入要隐藏的文件名,支持*号通配符回车确认添加...

第2步---MySQL卸载和图形化工具展示
第2步---MySQL卸载和图形化工具展示 1.MySQL的卸载 2.MySQL的图形化工具 2.1常见的图形化工具 SQLyog:简单。SQLyog首页、文档和下载 - MySQL 客户端工具 - OSCHINA - 中文开源技术交流社区 Mysql Workbench :MySQL :: MySQL Workbench DataGrip&…...

原型和原型链
好久没记了有点忘记了,来记录一下。 1、函数和对象的关系:对象都是通过函数创建的,函数也是一个对象。 2、原型和原型链 1.原型:原型分为两种 prototype:每一个函数都会有prototype属性,它指向函数的原型…...
解决ios隔空播放音频到macos没有声音的问题
解决ios隔空播放音频到macos没有声音的问题 一、检查隔空播放支持设备和系统要求二、打开隔空播放接收器三、重置MAC控制中心进程END 一、检查隔空播放支持设备和系统要求 Mac、iPhone、iPad 和 Apple Watch 上“连续互通”的系统要求 二、打开隔空播放接收器 ps;我设备是同一…...
LTPP在线开发平台【使用教程】
LTPP在线开发平台 点击访问 LTPP在线开发平台 LTPP(Learning teaching practice platform)在线开发平台是一个编程学习网站,该网站集文章学习、短视频、在线直播、代码训练、在线问答、在线聊天和在线商店于一体,专注于提升用户编…...

0818 新增码表 git拉取代码
目的是新增两个码表字段。然后和前端联调。 use db; delete from sys_dict_data where dict_type res_switch_status; INSERT INTO sys_dict_data VALUES (0, 1, 已接入, 1, res_switch_status, NULL, default, N, 0, , 2022-07-26 10:43:41, , NULL, NULL); INSERT INTO sys…...

AI 绘画Stable Diffusion 研究(十)sd图生图功能详解-精美二维码的制作
免责声明: 本案例所用安装包免费提供,无任何盈利目的。 大家好,我是风雨无阻。 为了让大家更直观的了解图生图功能,明白图生图功能到底是干嘛的,能做什么事情?今天我们继续介绍图生图的实用案例-精美二维码的制作。 对…...
报错)
C# File.ReadAllLines()报错
项目中需要读取一个文本文件的内容,调用C#的File.ReadAllLines(path)方法,但是报错,就提示unknown exception,也没其他提示了。 文件是在的,并且,如果把文件拷贝到另外一个路径,再次读取是正常…...
LeetCode 1162. As Far from Land as Possible【多源BFS】中等
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章…...

【算法】二分查找(整数二分和浮点数二分)
二分查找也称折半查找(Binary Search),是一种效率较高的查找方法,时间复杂度为O(logN)。 二分查找采用了“分治”策略。使用二分查找时,数组中的元素之间得有单调性(升序或者降序)。 二分的模…...
git压缩/合并多次commit提交为1次commit提交
git压缩/合并N次commit提交为1次commit提交 假设有最近3次提交: commit_id1 commit_id2 commit_id3目标是把以上3次commit合并成1个commit,注意,最新的commit提交在最上面。 在git bash里面的操作步骤: (1࿰…...
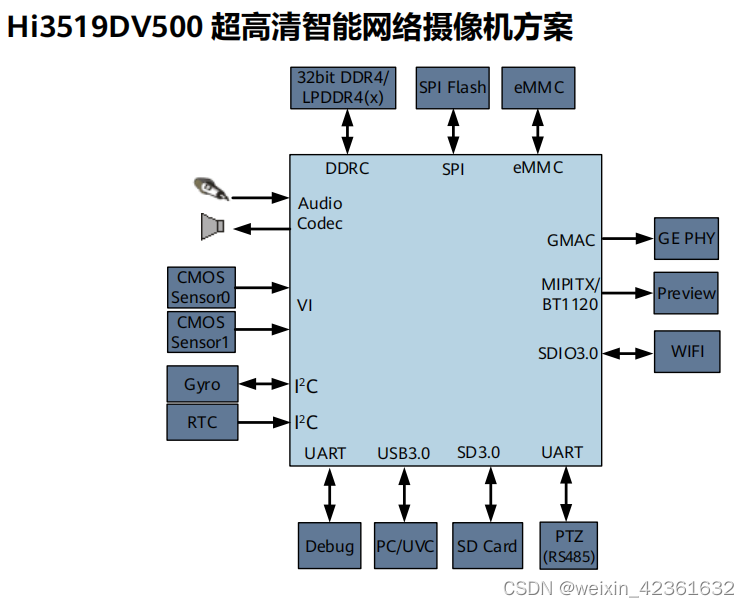
【3519DV500】AI算法承载硬件平台_2.5T算力+AI ISP图像处理_超感光视频硬件方案开发
Hi3519DV500 内置双核 A55 ,提供高效、丰富和灵活的CPU 资源,以满足客户计算和控制需求。 Hi3519DV500集成了高效的神经网络推理引擎,最高2.5Tops NN算力,支持业界主流的神经 网络框架。神经网络支持完整的 API 和工具链…...

Linux系统基础服务启动的方法
服务,其实就是运行在操作系统后台的一个或者多个应用程序,为计算机系统或用户提供某项特定的服务。Linux系统运行的绝大多数服务都是需要安装才有的,例如FTP服务、httpd服务、MySQL、redis、Zookeeper、rabbitmq、vsftpd等等,那么…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...

0x-3-Oracle 23 ai-sqlcl 25.1 集成安装-配置和优化
是不是受够了安装了oracle database之后sqlplus的简陋,无法删除无法上下翻页的苦恼。 可以安装readline和rlwrap插件的话,配置.bahs_profile后也能解决上下翻页这些,但是很多生产环境无法安装rpm包。 oracle提供了sqlcl免费许可,…...

webpack面试题
面试题:webpack介绍和简单使用 一、webpack(模块化打包工具)1. webpack是把项目当作一个整体,通过给定的一个主文件,webpack将从这个主文件开始找到你项目当中的所有依赖文件,使用loaders来处理它们&#x…...

用 FFmpeg 实现 RTMP 推流直播
RTMP(Real-Time Messaging Protocol) 是直播行业中常用的传输协议。 一般来说,直播服务商会给你: ✅ 一个 RTMP 推流地址(你推视频上去) ✅ 一个 HLS 或 FLV 拉流地址(观众观看用)…...
