卷积神经网络全解:(AlexNet/VGG/ GoogLeNet/LeNet/ResNet/卷积/激活/池化/全连接)、现代卷积神经网络、经典卷积神经网络
CNN,卷积神经网络,Convolution Neural Network
卷积计算公式:N = (W-F+2p)/s+1
这个公式每次都得看看,不能忘
1 经典网络
按照时间顺序
1.1 LeNet
LeNet是 Yann LeCun在1998年提出,用于解决手写数字识别的视觉任务。自那时起,CNN的最基本的架构就定下来了:卷积层、池化层、全连接层。
深度学习开山之作LeNet实战:(现代卷积神经网络/网络结构/原理解析/源码解读)、《Gradient-Based Learning Appliedto Document Recognition》_会害羞的杨卓越的博客-CSDN博客
1.2 AlexNet
深度学习奠基作AlexNet《ImageNet Classification with Deep Convolutional Neural Networks》之论文解读上篇_会害羞的杨卓越的博客-CSDN博客
AlexNet网络结构详解_会害羞的杨卓越的博客-CSDN博客
AlexNet是2012年ImageNet竞赛冠军获得者Hinton和他的学生Alex Krizhevsky设计的,把CNN的基本原理应用到了很深很宽的网络中。
主要参数:AlexNet网络包含8层,其中前5层为卷积-池化层,后3层为全连接层;输入224×224×3的图像,第一卷积层用96个11×11×3的卷积核对进行滤波,步幅4像素;全连接的每层有4096个神经元,最后一个完全连接的层的输出被馈送到1000路SoftMax,它产生超过1000个类别标签的分布;整个网络共650000个神经元。
特点:
- 使用ReLU作为激活函数,并验证其效果在较深的网络超过了Sigmoid,成功解决了Sigmoid在网络较深时的梯度弥散问题
- 使用Dropout(丢弃学习)随机忽略一部分神经元防止过拟合
- 在CNN中使用重叠的最大池化。此前CNN中普遍使用平均池化,AlexNet全部使用最大池化,避免平均池化的模糊化效果
- 提出了LRN(Local Response Normalization,局部正规化)层,对局部神经元的活动创建竞争机制,使得其中响应比较大的值变得相对更大,并抑制其他反馈较小的神经元,增强了模型的泛化能力
- 使用CUDA加速深度卷积网络的训练,利用GPU强大的并行计算能力,处理神经网络训练时大量的矩阵运算
1.3 VGG
- 网络深度:16-19层
- 5组卷积-池化,3个全连接
- 三个全连接层,前两层都有4096通道,第三层共1000路及代表1000个标签类别;最后一层为softmax层
- 所有卷积层有相同的配置,即卷积核大小为3x3,步长为1,填充为1
深度学习奠基作VGG《Very Deep Convolutional Networks for Large-Scale Image Recognition》(现代卷积神经网络/网络结构)_会害羞的杨卓越的博客-CSDN博客
1.4 GoogleNet
深度学习奠基作GoogleNet《Very Deep Convolutional Networks for Large-Scale Image Recognition》(现代卷积神经网络/网络结构)_会害羞的杨卓越的博客-CSDN博客
1.5 ResNet
深度学习最强奠基作ResNet《Deep Residual Learning for Image Recognition》论文解读(上篇)_会害羞的杨卓越的博客-CSDN博客
2 网络结构
2.1 卷积层
通过卷积操作,进行特征提取和降维。
2.2 激活层
将前一层的输出,通过非线性的激活函数进行处理,用以模拟任意维度的函数,增强网络的表征能力。
常用的激活函数:
- 阶跃函数(用的较少)
- sigmoid函数:
- 优点:平滑,易求导
- 缺点:激活函数计算量大,反向传播求误差梯度时,求导涉及除法;反向传播时,很容易就会出现梯度消失的情况,从而无法完成深层网络的训练
- 改善方案:归一化,用sk-learn函数处理
- tanh函数 常用于NLP,其他类似sigmiod函数
- Relu函数(常用),优点:
- 更加有效率的梯度下降以及反向传播,避免了梯度爆炸和梯度消失问题
- 计算过程简单
- softmax函数,特点:多分类模型适用
2.3 池化
也称子采样层或下采样层(Subsampling Layer),目的是缩小高、长方向上的空间的运算,以降低计算量,提高泛化能力。
计算方式:
- Max池化:对于每个输入矩阵,我们将其切割成若干大小相等的正方形小块,对各个参与池化计算的区域取最大值,形成的新矩阵。在图像识别领域,主要使用Max池化
- Average池化:对于每个输入矩阵,我们将其切割成若干大小相等的正方形小块,对各个参与池化计算的区域计算平均值
池化层特征:
- 没有要学习的参数。池化层和卷积层不同,没有要学习的参数。池化只是从目标区域中取最大值(或者平均值),所以不存在要学习的参数
- 通道数不发生变化。经过池化运算,输入数据和输出数据的通道数不会发生变化
- 对微小的位置变化具有鲁棒性(健壮)。输入数据发生微小偏差时,池化仍会返回相同的结果
2.4 全连接层
这个网络层相当于多层感知机(Multi-Layer Perceptron,简称MLP),其在整个卷积神经网络中起到分类器的作用。
通过前面多个“卷积-激活-池化”层的反复处理,待处理的数据特性已有了显著提高:一方面,输入数据的维度已下降到可用传统的前馈全连接网络来处理了;另一方面,此时的全连接层输入的数据已不是“泥沙俱下、鱼龙混杂”,而是经过反复提纯过的结果,因此输出的分类品质要高得多。
相关文章:

卷积神经网络全解:(AlexNet/VGG/ GoogLeNet/LeNet/ResNet/卷积/激活/池化/全连接)、现代卷积神经网络、经典卷积神经网络
CNN,卷积神经网络,Convolution Neural Network 卷积计算公式:N (W-F2p)/s1 这个公式每次都得看看,不能忘 1 经典网络 按照时间顺序 1.1 LeNet LeNet是 Yann LeCun在1998年提出,用于解决手…...
简述)
WDM 模型(Windows Driver Model)简述
WDM 模型(Windows Driver Model) 是微软公司为 Windows98 和 Windows2000 的驱动程序设计的一种架构,在 WDM 驱动程序模型中,每个硬件设备 至少有两个驱动程序。其中一个为功能驱动程序,它了解硬件工作的所有细节,负 责初始化 …...

【算法刷题之数组篇(1)】
目录 1.leetcode-59. 螺旋矩阵 II(题2.题3相当于二分变形)2.leetcode-33. 搜索旋转排序数组3.leetcode-81. 搜索旋转排序数组 II(与题目2对比理解)(题4和题5都是排序双指针)4.leetcode-15. 三数之和5.leetcode-18. 四数之和6.leet…...

【数据挖掘】使用 Python 分析公共数据【01/10】
一、说明 本文讨论了如何使用 Python 使用 Pandas 库分析官方 COVID-19 病例数据。您将看到如何从实际数据集中收集见解,发现乍一看可能不那么明显的信息。特别是,本文中提供的示例说明了如何获取有关疾病在不同国家/地区传播速度的信息。 二、准备您的…...

html怎么插入视频?视频如何插入页面
html怎么插入视频?视频如何插入页面 HTML 的功能强大,基本所有的静态效果都可以在此轻松呈现,各种视频网站内有大量的视频内容,本篇文章教你如何在 html 中插入视频 代码如下: <!DOCTYPE html> <html> …...
游戏服务端性能测试
导语:近期经历了一系列的性能测试,涵盖了Web服务器和游戏服务器的领域。在这篇文章中,我将会对游戏服务端所做的测试进行详细整理和记录。需要注意的是,本文着重于记录,而并非深入的编程讨论。在这里,我将与…...
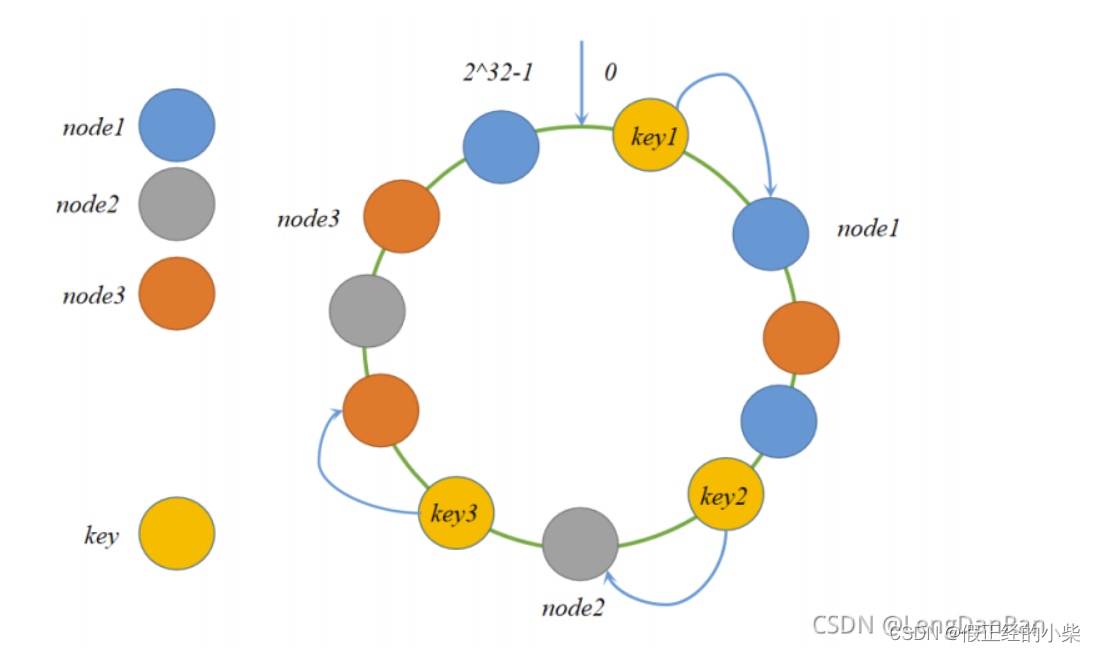
【使用Zookeeper当作注册中心】自己定制负载均衡常见策略
自己定制负载均衡常见策略 一、前言随机(Random)策略的实现轮询(Round Robin)策略的实现哈希(Hash)策略 一、前言 大伙肯定知道,在分布式开发中,目前使用较多的注册中心有以下几个&…...
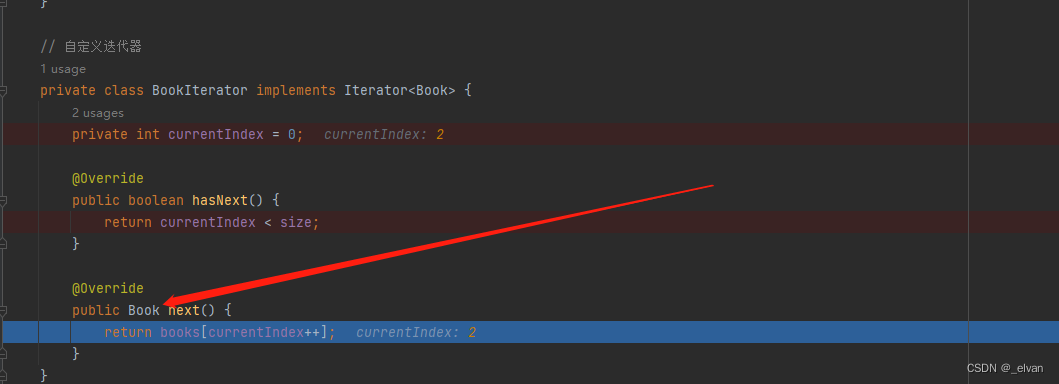
设计模式十七:迭代器模式(Iterator Pattern)
迭代器模式(Iterator Pattern)是一种行为型设计模式,它提供了一种访问聚合对象(例如列表、集合、数组等)中各个元素的方法,而无需暴露其内部表示。迭代器模式将遍历元素和访问元素的责任分离开来࿰…...

Python制作爱心并打包成手机端可执行文件
前言 本文是想要将python代码打包成在手机上能执行的文件 尝试了几个库, 有这也那样的限制,最终还是选了BeeWare 环境:python3.7.x 开始 找到打包有相关工具os-android-apk-builder,buildozer,cx_Freezeÿ…...
以及多容器通信和统一配置)
使用docker-compose.yml快速搭建开发、部署环境(nginx、tomcat、mysql、jar包、各种程序)以及多容器通信和统一配置
目录 docker-compose语法(更多说明可查看下面代码)imagehostnamecontainer_namevolumesnetworks yml文件的使用启动停止 开发环境(这里以python为例)部署环境nginxmysqltomcatjar包打包后的可执行程序 常见问题与解决方案多个容器…...

管理类联考——逻辑——真题篇——按知识分类——汇总篇——二、论证逻辑——支持加强——第三节——分类3——类比题干支持
文章目录 第三节 支持加强-分类3-类比题干支持真题(2017-28)-支持加强-正面支持-表达“确实如此”真题(2017-36)-支持加强-正面支持-表达“确实如此”真题(2017-39)-支持加强-正面支持-方法有效或方法可行,但多半不选择方法无恶果真题(2017-50)-支持加强真题(2018-2…...

搜索旋转排序数组
整数数组 nums 按升序排列,数组中的值 互不相同 。 在传递给函数之前,nums 在预先未知的某个下标 k(0 < k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k1], …, nums[n-1], nums[0], nums[1], …, …...

Steam搬砖项目:最长久稳定的副业!
项目应该大家都有听说话,但是细节问题,如何操作可能有些不是很清楚,今天在这里简单分享一下。 这个Steam搬砖项目主要赚钱汇率差和价值差,是一个细分领取的小项目。 不用引流,时间也是比较自由的,你可以兼…...
最小化安装移动云大云操作系统--BCLinux-R8-U8-Server-x86_64-230802版
CentOS 结束技术支持,转为RHEL的前置stream版本后,国内开源Linux服务器OS生态转向了开源龙蜥和开源欧拉两大开源社区,对应衍生出了一系列商用Linux服务器系统。BC-Linux V8.8是中国移动基于龙蜥社区Anolis OS 8.8版本深度定制的企业级X86服务…...

神经网络基础-神经网络补充概念-05-导数
概念 导数是微积分中的一个概念,用于描述函数在某一点的变化率。在数学中,函数的导数表示函数值随着自变量的微小变化而产生的变化量,即斜率或变化率。 假设有一个函数 f(x),其中 x 是自变量,y f(x) 是因变量。函数…...

kubernetes — 安装Ingress
1、 Ingress 1、安装-Nginx-Ingress kubectl apply -f https://raw.githubusercontent.com/kubernetes/ingress-nginx/controller-v1.8.1/deploy/static/provider/cloud/deploy.yaml 2、设为默认的Ingress [rootk8s01 ~]# vim default_ingress.yaml apiVersion: networking.…...

SSR使用HTTPS
1.安装 npm i browser-sync 2. 再angular.json里配置 "serve-ssr": {"builder": "nguniversal/builders:ssr-dev-server","options": {"ssl": true,"sslCert": "./node_modules/browser-sync/certs/server…...

Spring Boot中使用validator如何实现接口入参自动检验
文章目录 一、背景二、使用三、举例 一、背景 在项目开发过程中,经常会对一些字段进行校验,比如字段的非空校验、字段的长度校验等,如果在每个需要的地方写一堆if else 会让你的代码变的冗余笨重且相对不好维护,如何更加规范和优…...

thinkphp 5 实现UNION ALL 3个联表查询,并且带上搜索条件,名称,时间,手机号
在ThinkPHP 5中实现带有搜索条件、名称、时间和手机号的3个联表查询(UNION ALL),您可以按照以下步骤进行操作: 确保已经配置好数据库连接信息和相关的模型。 使用union()方法来构建3个联表查询,同时在每个查询中添加所…...
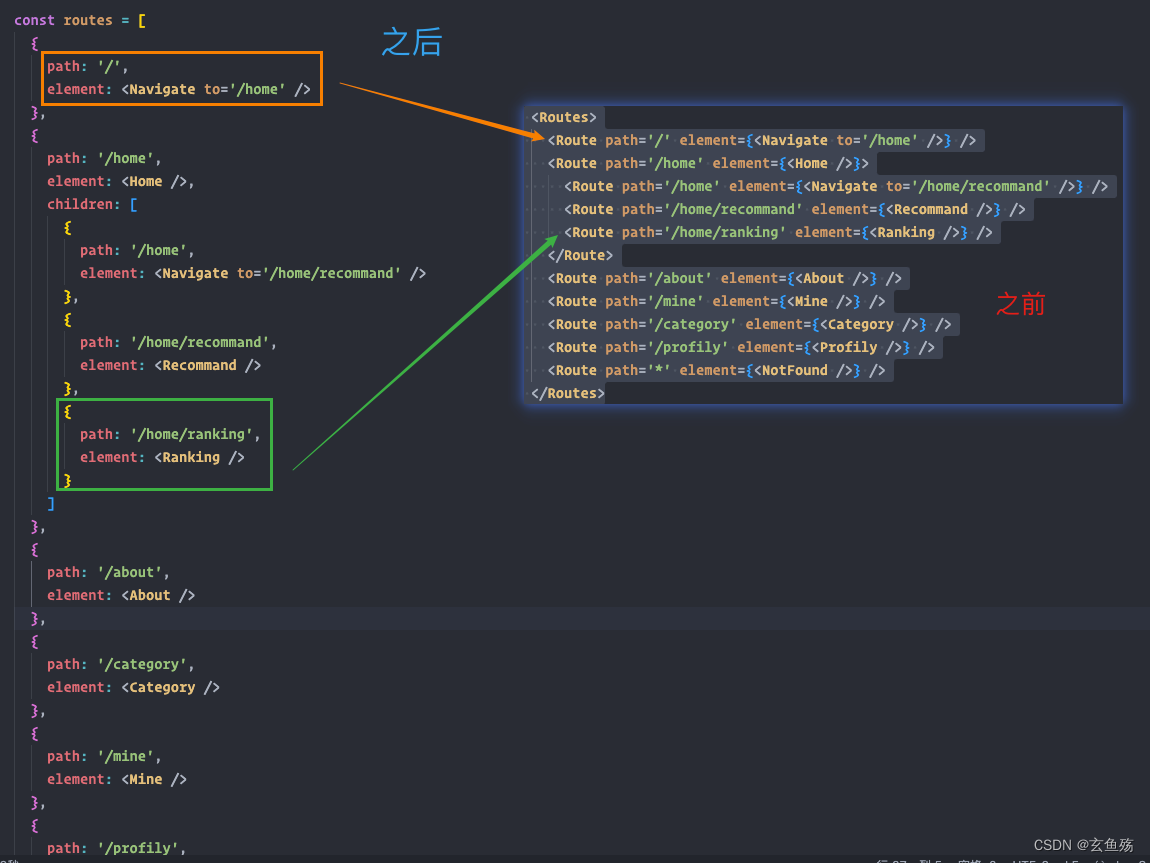
React 之 Router - 路由详解
一、Router的基本使用 1. 安装react-router react-router会包含一些react-native的内容,web开发并不需要 npm install react-router-dom 2. 设置使用模式 BrowserRouter或HashRouter Router中包含了对路径改变的监听,并且会将相应的路径传递给子组件Bro…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...
