Codeforces EDU 151 Div.2
文章目录
- A. Forbidden Integer
- B. Come Together
- C. Strong Password
- D. Rating System
- E. Boxes and Balls
A. Forbidden Integer
Problem - A - Codeforces
给定整数n,从1~k中选择除了x的数,使这些数之和为n,每个数可以选择无限次
爆搜,从k搜索到1,若当前搜索的数之和为n,返回true
#include <iostream>
using namespace std;const int N = 110;
int T, n, x, k;
int idx, p[N];bool dfs(int s, int start)
{if (start == -1) return false;if (s >= n) return s == n;for (int i = start; i >= 1; -- i ){if (i != x){p[idx ++ ] = i;if (dfs(s + i, start)) return true;idx -- ;}}return dfs(s, start - 1);
}int main()
{cin >> T;while ( T -- ){cin >> n >> k >> x;idx = 0;if (dfs(0, k)){puts("YES");cout << idx << endl;for (int i = 0; i < idx; ++ i ) cout << p[i] << ' ';cout << endl;}else puts("NO");}return 0;
}
B. Come Together
Problem - B - Codeforces
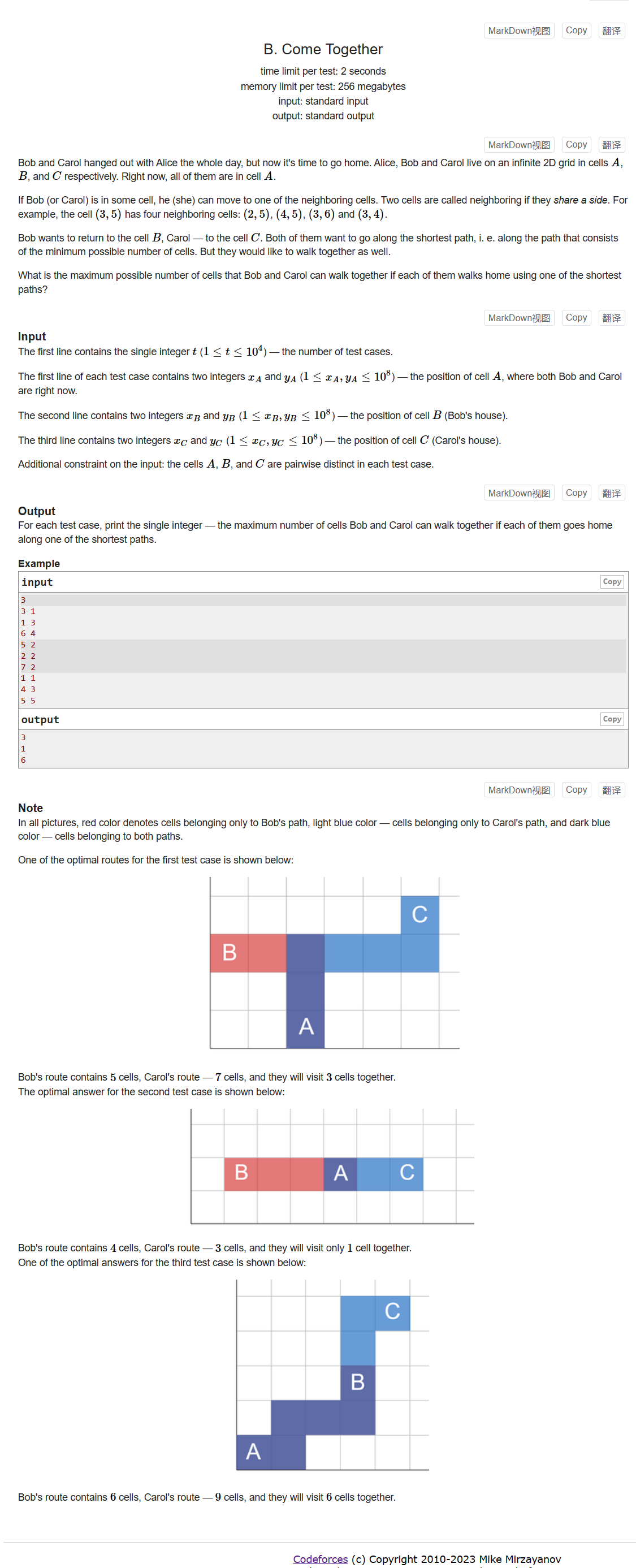
给定三个点,A为起点,BC为终点,从起点走到两个终点的最短路中,最长的公共路径长度是多少?
这是个我的错误思路:一开始以为是bfs最短路,想着在bfs的过程中记录路径
但是矩阵中没有障碍物,完全没有必要bfs,直接将起点于终点的横纵坐标之差相加,就是最短距离了
你可以发现,所有最短路中,无论怎么走,横向距离都是起点与终点的横坐标之差,当然纵向距离也是,所以有了以上结论
那么两条最短路的公共路径呢?将横纵方向分开来看,对于横坐标,若两者的终点都在起点的同一方向(都位于左边或左边),此时横向的最短距离等于横向距离离起点近的终点的横向距离,即 m i n ( x b , x c ) min(x_b, x_c) min(xb,xc)。若两者位于起点的左右两边,那么在横向距离上两者没有公共路径。同理,纵向距离也是如此
#include <iostream>
using namespace std;typedef long long LL;
LL T, xa, ya, xb, yb, xc, yc;int main()
{cin >> T;while ( T -- ){int ans = 0;cin >> xa >> ya >> xb >> yb >> xc >> yc;xb -= xa, yb -= ya, xc -= xa, yc -= ya; // 以a为源点if ((xb > 0) == (xc > 0)) ans += min(abs(xb), abs(xc));if ((yb > 0) == (yc > 0)) ans += min(abs(yb), abs(yc));cout << ans + 1 << endl;}return 0;
}
debug:若用xb * xc > 0判断两点是否位于源点的同一方向,相乘会爆int
C. Strong Password
Problem - C - Codeforces
题目只要求输出YES和NO,没有要求输出具体的序列,所以这题不用想得太复杂
比较暴力的解法是枚举所有可能的序列,用爆搜判断该序列是否为s的子序列,只要有一个序列不是s的子序列就输出YES,否则输出NO
考虑暴力如何优化?两个优化方向:枚举所有可能的序列和爆搜判断
枚举所有可能的序列不太好优化
关于爆搜的优化:由于s中只有字符19,可以预处理出第i个字符右边(包括第i个字符),19第一次出现的位置,若没有出现,位置用无穷表示
枚举t串时,t串的每个字符都有一个范围,假设t串的字符在s串中出现的下标为 x x x,若 x x x越大,s串中用来组成t串的字符就越少,出现相同子序列的概率就越低
以上贪心策略用反证法可以证明正确性,因此对于t串的每个字符,根据每个字符的范围以及字符在s串中出现的位置,确定一个下标最大的字符即可
遇到无穷直接输出YES即可
#include <iostream>
#include <cstring>
using namespace std;const int N = 3e5 + 10, M = 15;
char s[N], l[M], r[M];
int last[N][M], T, m;int main()
{ios::sync_with_stdio(false);cin.tie(nullptr);cin >> T;while ( T -- ){cin >> s >> m >> l >> r;int len = strlen(s);memset(last[len], 0x3f, sizeof last[len]);for (int i = len - 1; i >= 0; -- i ){memcpy(last[i], last[i + 1], sizeof last[i + 1]);last[i][s[i] - '0'] = i;}int cur = -1; // cur和next为搜索s串的双指针for (int i = 0; i < m && cur != 0x3f3f3f3f; ++ i ){int next = 0;for (int j = l[i] - '0'; j <= r[i] - '0'; ++ j ){next = max(next, last[cur + 1][j]);} cur = next;}cout << (cur == 0x3f3f3f3f ? "YES\n" : "NO\n");}return 0;
}
debug:如果memset(last[len], 0x3f, sizeof last[len])写成memset(last, 0x3f, sizeof last),直接memset整个last数组会TLE的,考虑到预处理的顺序,只要初始化最后一个一维数组即可last[len]
D. Rating System
Problem - D - Codeforces
看着像是求最大子段和,一开始也是这么想的,但是仔细一想却是不对的
参考视频:最小子段和 动态规划【Codeforces EDU 151】_哔哩哔哩_bilibili
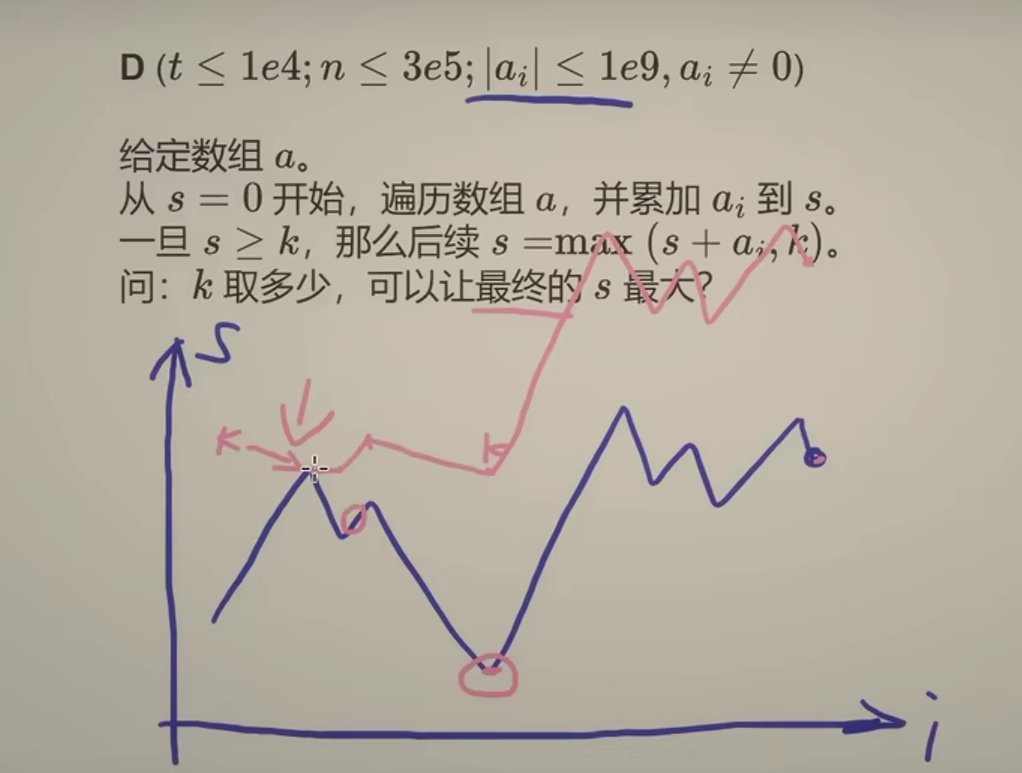
确定一个k值,使分数大于等于k值后不会小于k值,也就是说:抵消分数递达k之后的减分行为
问k为多少,最后的分数最高?显然,抵消的分数越多,最后的分数越高
题目给定每一次分数的变化,即用 a i a_i ai的正负表示分数的加减变化。若要抵消最多的减分,就要找出数组中的最小连续子段和 [ a i , a r ] [a_i, a_r] [ai,ar],再将k设置为 s u m ( a 0 , a i − 1 ) sum(a_0, a_{i-1}) sum(a0,ai−1)
通常求最小子段和,都是使用dp,然而这题求的并不是具体的最小子段和,这题求的是最小子段和的左区间,以及一个前缀和信息。因此只需要在求前缀和的过程中,维护最小子段和的左区间信息即可
#include <iostream>
using namespace std;typedef long long LL;
const int N = 3e5 + 10;
int a[N], T;int main()
{cin >> T;while ( T -- ){int n;cin >> n;for (int i = 0; i < n; ++ i ) cin >> a[i];LL ans = 0, sum = 0, cmax = 0, k;for (int i = 0; i < n; ++ i ){sum += a[i];cmax = max(cmax, sum);LL val = cmax - sum;if (ans < val){ans = val;k = cmax;}}cout << k << endl;}return 0;
}
E. Boxes and Balls
Problem - E - Codeforces
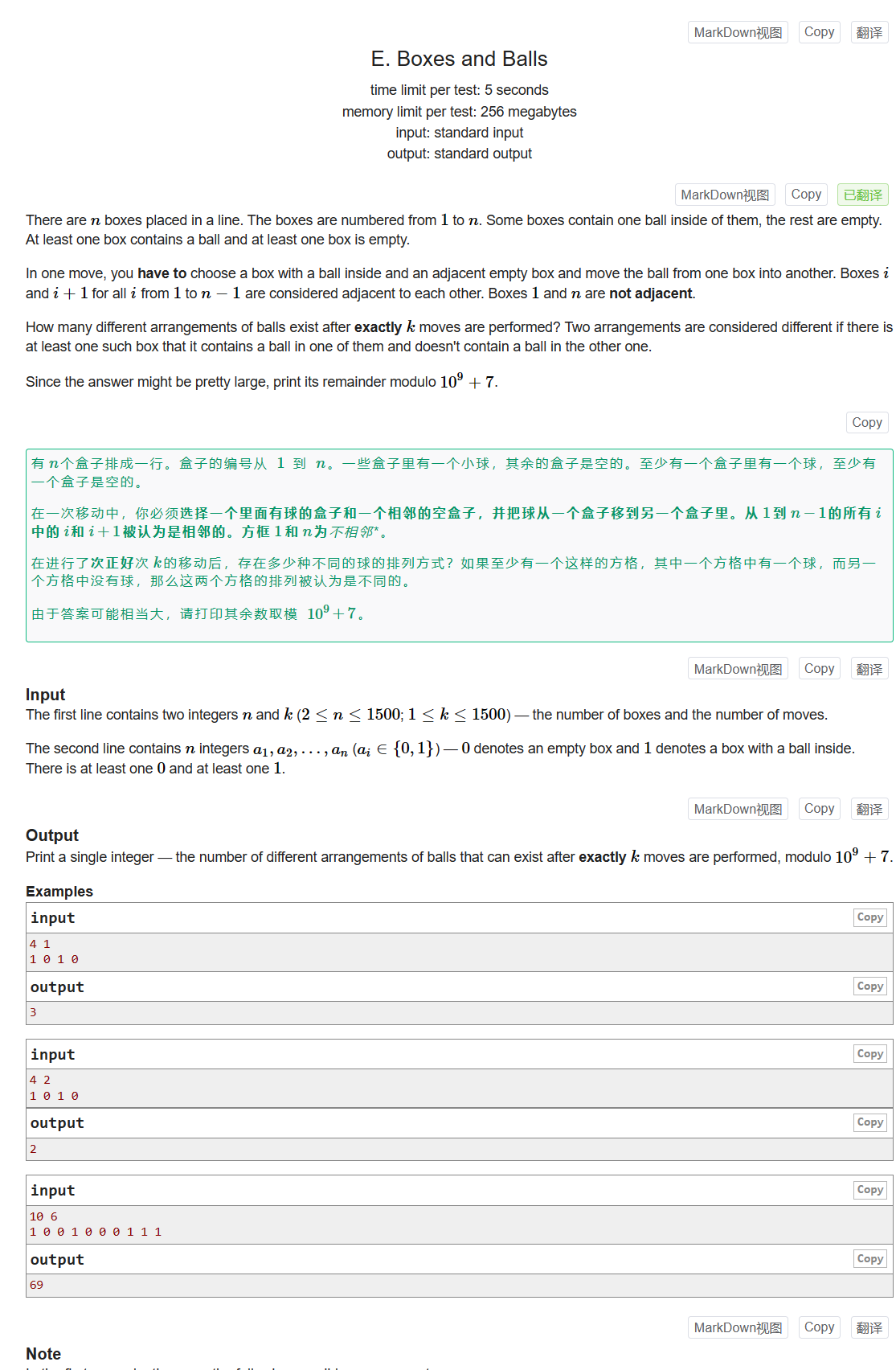
数组中有n个0和1,至少有一个0和1,每次选择一对相邻的0和1进行交换,问经过k次交换后,存在多少种不同的数组?
有些难,以后再来补
相关文章:

Codeforces EDU 151 Div.2
文章目录 A. Forbidden IntegerB. Come TogetherC. Strong PasswordD. Rating SystemE. Boxes and Balls A. Forbidden Integer Problem - A - Codeforces 给定整数n,从1~k中选择除了x的数,使这些数之和为n,每个数可以选择无限次 爆搜&…...
V2board缓存投毒漏洞复现
1.什么是缓存投毒 缓存投毒(Cache poisoning),通常也称为域名系统投毒(domain name system poisoning),或DNS缓存投毒(DNS cache poisoning)。它是利用虚假Internet地址替换掉域名系…...
2023面试八股文 ——Java基础知识
Java基础知识 一.Java概述何为编程什么是Javajdk1.5之后的三大版本JVM、JRE和JDK的关系什么是跨平台性?原理是什么Java语言有哪些特点什么是字节码?采用字节码的大好处是什么什么是Java程序的主类?应用程序和小程序的主类有何不同?…...

在linux系统中修改mysql数据目录
目录 1.查看mysql默认存储路径2.停止mysql服务3.移动或复制原数据目录4.修改配置文件5.修改启动文件6.配置AppArmor访问控制规则7.重启apparmor服务8.启动mysql 1.查看mysql默认存储路径 在/etc/mysql/mysql.conf.d/mysqld.cnf中的datadir配置项。 datadir /var/lib/mysql2…...

ORB-SLAM2学习笔记9之图像帧Frame
先占坑,明天再完善… 文章目录 0 引言1 Frame类1.1 成员函数1.2 成员变量 2 Frame类的用途 0 引言 ORB-SLAM2学习笔记8详细了解了图像特征点提取和描述子的生成,本文在此基础上,继续学习ORB-SLAM2中的图像帧,也就是Frame类&#…...
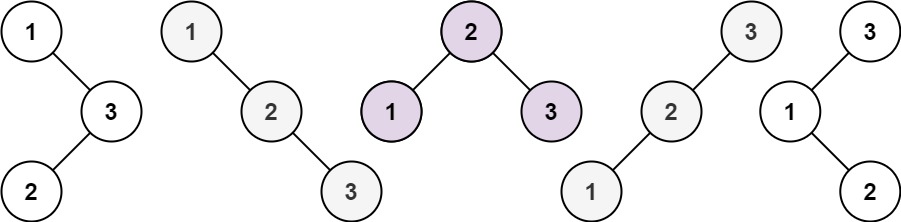
面试热题(不同的二分搜索树)
给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。 经典的面试题,这部分涉及了组合数学中的卡特兰数,如果对其不清楚的同学可以去看我以前的博客卡特兰数 …...

MybatisPlus整合p6spy组件SQL分析
目录 p6spy java为什么需要 如何使用 其他配置 p6spy p6spy是一个开源项目,通常使用它来跟踪数据库操作,查看程序运行过程中执行的sql语句。 p6spy将应用的数据源给劫持了,应用操作数据库其实在调用p6spy的数据源,p6spy劫持到…...
项目实战 — 博客系统③ {功能实现}
目录 一、编写注册功能 🍅 1、使用ajax构造请求(前端) 🍅 2、统一处理 🎄 统一对象处理 🎄 保底统一返回处理 🎄 统一异常处理 🍅 3、处理请求 二、编写登录功能 🍅 …...
卷积神经网络全解:(AlexNet/VGG/ GoogLeNet/LeNet/ResNet/卷积/激活/池化/全连接)、现代卷积神经网络、经典卷积神经网络
CNN,卷积神经网络,Convolution Neural Network 卷积计算公式:N (W-F2p)/s1 这个公式每次都得看看,不能忘 1 经典网络 按照时间顺序 1.1 LeNet LeNet是 Yann LeCun在1998年提出,用于解决手…...
简述)
WDM 模型(Windows Driver Model)简述
WDM 模型(Windows Driver Model) 是微软公司为 Windows98 和 Windows2000 的驱动程序设计的一种架构,在 WDM 驱动程序模型中,每个硬件设备 至少有两个驱动程序。其中一个为功能驱动程序,它了解硬件工作的所有细节,负 责初始化 …...

【算法刷题之数组篇(1)】
目录 1.leetcode-59. 螺旋矩阵 II(题2.题3相当于二分变形)2.leetcode-33. 搜索旋转排序数组3.leetcode-81. 搜索旋转排序数组 II(与题目2对比理解)(题4和题5都是排序双指针)4.leetcode-15. 三数之和5.leetcode-18. 四数之和6.leet…...

【数据挖掘】使用 Python 分析公共数据【01/10】
一、说明 本文讨论了如何使用 Python 使用 Pandas 库分析官方 COVID-19 病例数据。您将看到如何从实际数据集中收集见解,发现乍一看可能不那么明显的信息。特别是,本文中提供的示例说明了如何获取有关疾病在不同国家/地区传播速度的信息。 二、准备您的…...

html怎么插入视频?视频如何插入页面
html怎么插入视频?视频如何插入页面 HTML 的功能强大,基本所有的静态效果都可以在此轻松呈现,各种视频网站内有大量的视频内容,本篇文章教你如何在 html 中插入视频 代码如下: <!DOCTYPE html> <html> …...
游戏服务端性能测试
导语:近期经历了一系列的性能测试,涵盖了Web服务器和游戏服务器的领域。在这篇文章中,我将会对游戏服务端所做的测试进行详细整理和记录。需要注意的是,本文着重于记录,而并非深入的编程讨论。在这里,我将与…...
【使用Zookeeper当作注册中心】自己定制负载均衡常见策略
自己定制负载均衡常见策略 一、前言随机(Random)策略的实现轮询(Round Robin)策略的实现哈希(Hash)策略 一、前言 大伙肯定知道,在分布式开发中,目前使用较多的注册中心有以下几个&…...
设计模式十七:迭代器模式(Iterator Pattern)
迭代器模式(Iterator Pattern)是一种行为型设计模式,它提供了一种访问聚合对象(例如列表、集合、数组等)中各个元素的方法,而无需暴露其内部表示。迭代器模式将遍历元素和访问元素的责任分离开来࿰…...

Python制作爱心并打包成手机端可执行文件
前言 本文是想要将python代码打包成在手机上能执行的文件 尝试了几个库, 有这也那样的限制,最终还是选了BeeWare 环境:python3.7.x 开始 找到打包有相关工具os-android-apk-builder,buildozer,cx_Freezeÿ…...
以及多容器通信和统一配置)
使用docker-compose.yml快速搭建开发、部署环境(nginx、tomcat、mysql、jar包、各种程序)以及多容器通信和统一配置
目录 docker-compose语法(更多说明可查看下面代码)imagehostnamecontainer_namevolumesnetworks yml文件的使用启动停止 开发环境(这里以python为例)部署环境nginxmysqltomcatjar包打包后的可执行程序 常见问题与解决方案多个容器…...

管理类联考——逻辑——真题篇——按知识分类——汇总篇——二、论证逻辑——支持加强——第三节——分类3——类比题干支持
文章目录 第三节 支持加强-分类3-类比题干支持真题(2017-28)-支持加强-正面支持-表达“确实如此”真题(2017-36)-支持加强-正面支持-表达“确实如此”真题(2017-39)-支持加强-正面支持-方法有效或方法可行,但多半不选择方法无恶果真题(2017-50)-支持加强真题(2018-2…...

搜索旋转排序数组
整数数组 nums 按升序排列,数组中的值 互不相同 。 在传递给函数之前,nums 在预先未知的某个下标 k(0 < k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k1], …, nums[n-1], nums[0], nums[1], …, …...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...
