2023国赛数学建模A题思路模型代码汇总 高教社杯
本次比赛我们将会全程更新思路模型及代码,大家查看文末名片获取
之前国赛相关的资料和助攻可以查看
2022数学建模国赛C题思路分析_2022国赛c题matlab_UST数模社_的博客-CSDN博客
2022国赛数学建模A题B题C题D题资料思路汇总 高教社杯_2022国赛c题matlab_UST数模社_的博客-CSDN博客
我们国赛更新的流程如下:
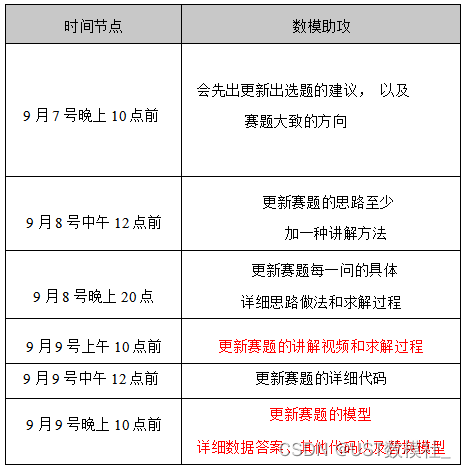
A题思路:
(比赛开始以后第一时间更新)
国赛建模常见算法汇总
在国赛开始前,给大家总结了数学建模的常用算法,大家可以参考借鉴学习。
国赛数学建模常见问题分为:
1.分类问题
2.预测问题
3.优化问题
4.评价问题
4.1 分类问题
判别分析
距离判别法
Fisher判别法
Bayes判别法
逐步判别法
聚类分析
系统聚类法(分层聚类法)
快速聚类法(K-均值聚类法)
两步聚类法(智能聚类方法)
模糊聚类分析
与遗传算法、神经网络或灰色理论联合的聚类方法
神经网络分类方法
4.2预测问题
回归分析法
时间序列分析法
灰色预测法
BP神经网络法
组合预测法
4.3 优化问题
数学规划模型
微分方程组模型
图论与网络优化问题
概率模型
组合优化经典问题
多维背包问题(MKP)
二维指派问题(QAP)
旅行商问题(TSP)
车辆路径问题(VRP)
车间作业调度问题(JSP)
4.4 评价问题
层次分析法(AHP)
灰色综合评价法(灰色关联度分析)
模糊综合评价法
BP神经网络综合评价法
数据包络法(DEA)
组合评价法
如何成为一个数学建模高手
1、扎实的基础
这里所谓的基础并不是单独指的数学的基础,而是指的一些基础的知识也许就是一些常识,包括数学、物理、化学、生物、地理等方面。当然这些知识并不一定都是课堂上学到的,有些来自于生活。建模也许人人都会,但是不是人人都能建立出优秀的模型,当你发现你对一些现实生活中的小问题都没有思路的时候,不是你没有数学的天赋,而是你缺少对于生活中知识的积累。不要一开始就去问学微积分有什么用,
你要做的就是先把它学了,就算是记下来了也行,这样你就不会在遇到类似“用最少的钱办最多的事”这样最常见的问题时感到无从下手。因此我们要做的就是尽可能多的涉猎知识,不要仅仅拘泥于自己的专业。
2、丰富的想像力
不要拘泥于固定的思维方式,遇到问题的时候要多想几种解决问题的方案,试试别人从没想过的方法。不要一拿到问题就首先将问题分类,好多人愿意一上来就先将问题分类,例如分为优化问题,组合问题,方程问题等等。然后用与该分类相关的一些方法去解决问题。现实的问题很多都是非常复杂的,单纯的分类有时候是没有任何意义的。这样做不但局限了你的思想,而且会使你变得更加固执。丰富的想像力会把你和问题拉得更近,开阔的思维可以让你看到问题的各个方面。当然丰富的想像力是建立在丰富的知识基础之上的。
3、最简单的是最好的
这也许是所有科学都遵循的一条准则,复杂的质能转换原理在爱因斯坦眼里不过是一个简单得不能再简单的公式:E=mc2。简单的方法更容易被人理解,更容易实现,也更容易维护。遇到问题时要优先考虑最简单的方案,只有简单方案不能满足要求时再考虑复杂的方案。当然即使要应用复杂的方案,也要采用循序渐进的思想,逐步地改进前一个方案,不要一开始就尝试非常复杂的方案。
4、不钻牛角尖
当你遇到障碍的时候,不妨暂时远离问题,看看窗外的风景,听听轻音乐,和朋友聊聊天,或者可以看几本小说。当我遇到难题的时候我通常会去找朋友聊天,朋友的一些善意的小建议甚至是鼓励都会使我的大脑得到充分的休息。当重新开始工作的时候,我会发现那些难题现在竟然可以迎刃而解了。
5、对答案的渴求
人类自然科学的发展史就是一个渴求得到答案的过程,即使只能知道答案的一小部分也值得我们去付出。只要你坚定信念,一定要找到问题的答案,你才会付出精力去探索,即使最后没有得到答案,在过程中你也会学到很多东西。
6、多与别人交流
三人行必有我师,也许在一次和别人不经意的谈话中,就可以迸出灵感的火花。多上上网,看看别人对同一问题的看法,会给你很大的启发。当然不要把和别人交流的目的就看作是去获取问题的答案,即使是学习方法的交流对你来说都是有益的。
7、良好的编程素养
随着科学的不断进步,越来越多的学科已经和计算机密不可分了,作为解决现实问题的主要手段之一的数学建模当然是离不开计算机了。有的人可能会认为搞数学建模的只要可以编写一些简单的程序就可以了,我对这一点持否定态度。对于编程来说,不管程序量的大小都是一个工程,既然是工程就要按照质量标准来做,不是有ISO9000质量标准吗?那个标准对于编程同样适用。只有编程的质量得到了保证,计算机这个工具才能真正成为建模的有利武器。
8、韧性和毅力
这也许是“高手”和一般人最大的区别。高手们并不是天才,他们是在无数个日日夜夜中磨炼出来的。成功能给我们带来无比的喜悦,但过程却是无比的枯燥乏味。你不妨做个测试,坚持每天去图书馆看1个小时的和数学建模相关的书或资料,坚持半年,如果能够不间断地完成这一工作,你就可以满足这一条。
相关文章:

2023国赛数学建模A题思路模型代码汇总 高教社杯
本次比赛我们将会全程更新思路模型及代码,大家查看文末名片获取 之前国赛相关的资料和助攻可以查看 2022数学建模国赛C题思路分析_2022国赛c题matlab_UST数模社_的博客-CSDN博客 2022国赛数学建模A题B题C题D题资料思路汇总 高教社杯_2022国赛c题matlab_UST数模社…...

vue3如何批量设置动态ref
示例如下: <template v-for"item in selectList"><el-select v-model"item.value" :ref"el > setRef(el, item)"><el-optionv-for"v in item.options":key"v.value":label"v.label"…...
Android Studio run app 设置 release 模式
背景 为验证我们的 SDK 集成在客户应用上的质量,需要我们的测试环境尽量的与客户应用保持一致。客户普遍都会打 release 包并混淆,然后进行上线应用,因此我们在测试过程中也需要使用 release 包进行验证。对于 Android Studio 运行项目&…...

【SA8295P 源码分析】41 - SA8295所有镜像位置、拷贝脚本、生成QFIL包
【SA8295P 源码分析】41 - SA8295所有镜像位置、拷贝脚本、生成QFIL包 一、SA8295 各镜像位置二、SA8295 QNX 侧镜像拷贝脚本三、SA8295 Android 侧镜像拷贝脚本四、使用QFIL 下载整包五、Fastboot 下载命令整理系列文章汇总见:《【SA8295P 源码分析】00 - 系列文章链接汇总》…...

【Redis】Redisson分布式锁原理与使用
【Redis】Redisson分布式锁原理与使用 什么是Redisson? Redisson - 是一个高级的分布式协调Redis客服端,能帮助用户在分布式环境中轻松实现一些Java的对象,Redisson、Jedis、Lettuce 是三个不同的操作 Redis 的客户端,Jedis、Le…...

Segment Anything论文阅读笔记
Segment Anything论文阅读笔记 1. Segment Anything论文基本信息2. Segment Anything论文阅读2.1 第一遍阅读 Segment Anything2.2. 第二遍阅读 Segment Anything2.2.1. Segment Anything中相关的图表 1. Segment Anything论文基本信息 论文地址https://arxiv.org/abs/2304.02…...

Python入门教程 | Python 基础语法
标识符 第一个字符必须是字母表中字母或下划线 _ 。标识符的其他的部分由字母、数字和下划线组成。标识符对大小写敏感。 在 Python 3中,可以用中文作为变量名,非 ASCII 标识符也是允许的了。默认情况下,Python 3 源码文件以 UTF-8 编码&am…...

JAMstack架构:快速构建安全、高性能的现代应用
随着Web应用的快速发展,开发者们在寻找更加高效、安全和可维护的应用架构。JAMstack架构应运而生,它通过将前端、后端和部署过程分离,提供了一种现代化的方式来构建Web应用。在本文中,我们将深入探讨JAMstack架构的特点、优势以及…...
Web会话技术
会话:用户打开浏览器,访问web服务器的资源,会话建立,直到有一方断开连接,会话结束。在一次会话中可以包含多次请求和响应 会话跟踪:一种维护浏览器状态的方法,服务器需要识别多次请求是否来自于同一浏览器,…...

hbuilderx打包苹果证书获取步骤
简介: 目前app开发,很多企业都用H5框架来开发,而uniapp又是这些h5框架里面最成熟的,因此hbuilderx就成为了开发者的首选。然而,打包APP是需要证书的,那么这个证书又是如何获得呢? 生成苹果证书相对复杂一些…...

JAVA下载Excel文件之后无法打开,提示损坏
resources 目录下放模板 excel 文件,通过接口下载后,可以正常下载,但打不开。 问题: springboot 项目简单的下载excel 模板功能,模板放在resources/template/目录中 public void downloadItemBatch(HttpServletRespo…...

复合 类型
字符串和切片 切片 切片的作用是允许你引用集合中部分连续的元素序列,而不是引用整个集合。 例如: let s String::from("hello world");let hello &s[0..5]; // 切片 [0,5) 等效于&s[..5] let world &s[6..11]; // 切片…...
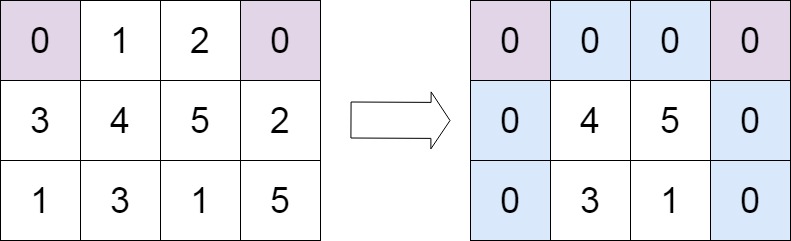
Practices11|41. 缺失的第一个正数(数组)、73. 矩阵置零(矩阵)
41. 缺失的第一个正数(数组) 1.题目: 给你一个未排序的整数数组 nums ,请你找出其中没有出现的最小的正整数。 请你实现时间复杂度为 O(n) 并且只使用常数级别额外空间的解决方案。 示例 1: 输入:nums [1,2,0] 输出…...

深入完整的带你了解java对象的比较
目录 元素的比较 1.基本类型的比较 2.对象比较的问题 1.运行结果 2.疑问 3.原因 对象的比较 1.覆写基类的equals 2.基于Comparble接口类的比较 3.基于比较器比较 4.三种方式对比 元素的比较 1.基本类型的比较 在Java 中,基本类型的对象可以直接比较大…...

ubuntu20.04升级GLIBC高版本方法,解决:version `GLIBC_2.34‘ not found
检查版本 strings /lib/x86_64-linux-gnu/libc.so.6 |grep GLIBC_ 1 显示结果 GLIBC_2.2.5 GLIBC_2.2.6 GLIBC_2.3 GLIBC_2.3.2 GLIBC_2.3.3 GLIBC_2.3.4 GLIBC_2.4 GLIBC_2.5 GLIBC_2.6 GLIBC_2.7 GLIBC_2.8 GLIBC_2.9 GLIBC_2.10 GLIBC_2.11 GLIBC_2.12 GLIBC_2.13 GLIBC_2…...

日产将使用东风纯电平台?官方回应:不是日产品牌
据财联社报道,日产中国在对于“日产将使用东风纯电平台”的传闻进行回应时指出,文中提及的平台将会用于日产在华合资企业的自主品牌,而不是日产品牌本身。这一消息进一步确认了之前每经网的报道,称日产将采用东风汽车最新发布的“…...
cdh6.3.2 Flink On Yarn taskmanager任务分配倾斜问题的解决办法
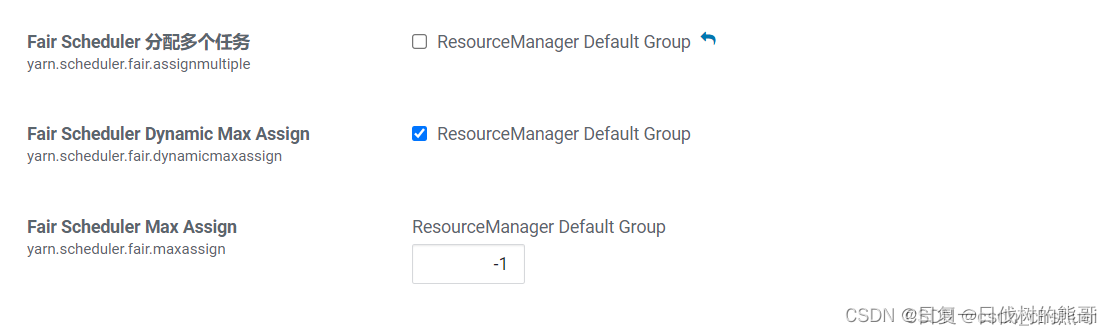
业务场景: Flink On Yarn任务启动 组件版本: CDH:6.3.2 Flink:1.13.2 Hadoop:3.0.0 问题描述: 在使用FLink on Yarn调度过程中,发现taskmanager总是分配在集中的几个节点上,集群…...
改进YOLO系列:3.添加SOCA注意力机制
添加SOCA注意力机制 1. SOCA注意力机制论文2. SOCA注意力机制原理3. SOCA注意力机制的配置3.1common.py配置3.2yolo.py配置3.3yaml文件配置1. SOCA注意力机制论文 暂未找到 2. SOCA注意力机制原理 3. SOCA注意力机制的配置 3.1common.py配置 ./models/common.p…...

SpringBoot整合Mybatis Plus——条件构造器Wrapper
Mybatis Plus为我们提供了如下的一些条件构造器,我们可以利用它们实现查询条件、删除条件、更新条件的构造。 条件构造器 | MyBatis-Plus (baomidou.com) 一、通过maven坐标引入依赖(注意版本!!) <dependency>…...

while循环语句
# while循环 # 通过while循环,计算1到100的总和 num 1 sum 0 while num < 100:sum num sumnum 1 print(f"1到100的和为{sum}") #嵌套语句--实现猜1-10数字游戏 import random flagTrue numrandom.randint(1,10) while flag:guess_numint(input(&q…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...
