BC77 有序序列插入一个数
描述
有一个有序数字序列,从小到大排序,将一个新输入的数插入到序列中,保证插入新数后,序列仍然是升序。
输入描述
第一行输入一个整数(0≤N≤50)。
第二行输入N个升序排列的整数,输入用空格分隔的N个整数。
第三行输入想要进行插入的一个整数。
输出描述
输出为一行,N+1个有序排列的整数。
思路:把数组中的每个元素从后往前和插入的数依次比较,直到遇到小于所插入元素的数,将待插入的数放到该数后边。
代码:
#include <stdio.h>
int main()
{int n=0;//输入个数scanf("%d",&n);//输入n个数int arr[51]={0};int i=0;for(i=0;i<n;i++){scanf("%d",&arr[i]);}//接收要插入的数int k=0;scanf("%d",&k);//插入k//数组从后往前一个一个和k比较for(i=n-1;i>=0;i--){if(arr[i] > k){arr[i+1] = arr[i]; }else {arr[i+1]=k;break;}}if(i<0){arr[0]=k;}for(i=0;i<n+1;i++){printf("%d ",arr[i]);}return 0;
}
相关文章:

BC77 有序序列插入一个数
描述 有一个有序数字序列,从小到大排序,将一个新输入的数插入到序列中,保证插入新数后,序列仍然是升序。 输入描述 第一行输入一个整数(0≤N≤50)。 第二行输入N个升序排列的整数,输入用空格分隔的N个整数。 第三…...
)
通过脚本使用Cppcheck做静态测试并生成报告(Windows)
1.安装cppcheck 先从cppcheck官方网站下载cppcheck的安装包。 注: (1)官网地址:https://sourceforge.net/projects/cppcheck (2)截止2023年8月,官方发布的最新版本是cppcheck-2.11-x64-Setup.…...

工业安全生产信息化平台的基本架构和关键功能分享
工业安全生产信息化平台是指利用信息技术手段,将工业安全生产管理与数据采集、传输、处理相结合,实现对工业安全生产全过程的数字化、信息化、智能化管理的平台。它通过集成多种信息系统和设备,实现对重大危险源监控预警、安全风险分级管控、…...

每日一道面试题之session 和 cookie 有什么区别?
Session和Cookie是两种在Web开发中用于跟踪用户状态的机制: 它们之间的区别如下: 存储位置:Cookie是存储在用户浏览器中的小型文本文件,而Session是存储在服务器上的数据结构。 数据安全性:Cookie中的数据可以被用户…...

SHELL 基础 显示字符颜色, 修改历史命令,Linux里的命令 执行顺序
echo 打印命令 : 显示字符串 : [rootserver ~]# echo this is SHELL language this is SHELL language [rootserver ~]# echo this is SHELL language this is SHELL language [rootserver ~]# echo "this is SHELL language" this is SH…...

Vue 和 JQuery 的区别在哪?为什么 JQuery 会被 Vue 取代?
在 Web 前端开发领域,我们经常会遇到一些不同的工具和框架,其中 Vue 和 JQuery, JQuery 是曾经备受欢迎的选择,而现在 Vue 是大多数人的选择。本文将探讨 Vue 和 JQuery 之间的区别,并讨论为什么越来越多的开发人员放弃 JQuery 而…...

Spring 中 Bean 注入与获取
Spring 中有哪些方式可以把 Bean 注入到 IOC 容器? 关于这个问题,我的回答入下:把 Bean 注入到 IOC 容器里面的方式有 7 种方式 1. 使用 xml 的方式来声明 Bean 的定义,Spring 容器在启动的时候会加载并解析这 个 xml,…...
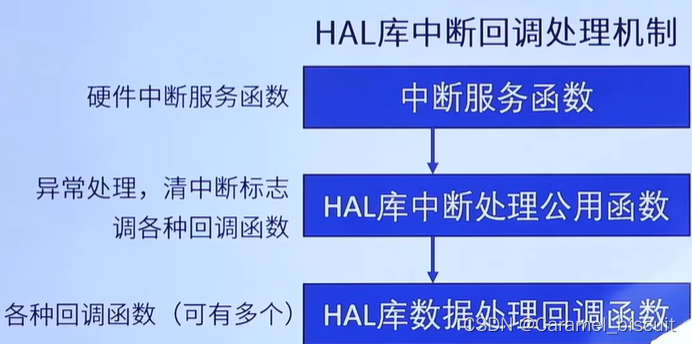
STM32 中断复习
中断 打断CPU执行正常的程序,转而处理紧急程序,然后返回原暂停的程序继续运行,就叫中断。 在确定时间内对相应事件作出响应,如:温度监控(定时器中断)。故障处理,检测到故障&#x…...
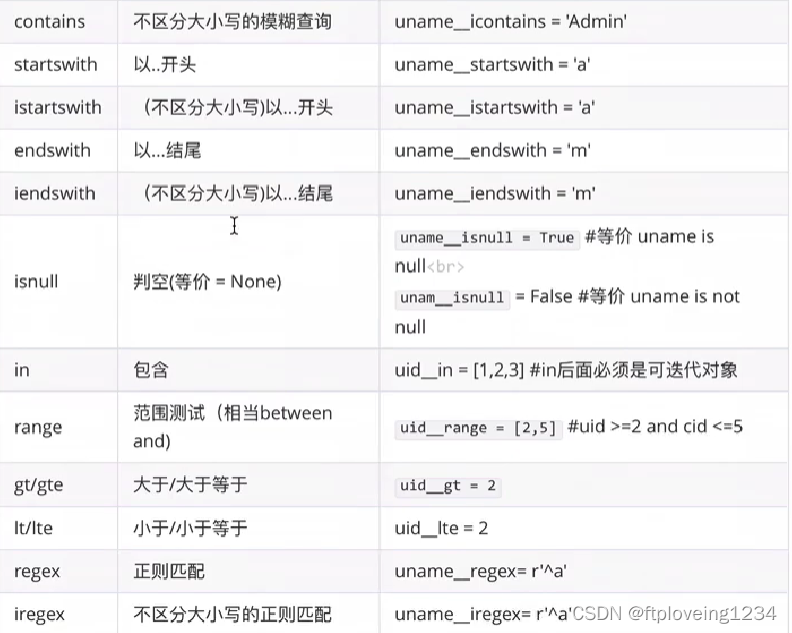
Django的模型
定义模型 from django.db import models class User(models.Model):# 类属性是表示表的字段username models.CharField(max_length50,uniqueTrue)password models.CharField(max_length200)create_time models.DateTimeField(auto_now_addTrue) # auto_now_add新增数据时间…...

非计算机科班如何丝滑转码
近年来,很多人想要从其他行业跳槽转入计算机领域。非计算机科班如何丝滑转码? 方向一:如何规划才能实现转码? 对于非计算机科班的人来说,想要在计算机领域实现顺利的转码并不是一件容易的事情,但也并非不…...

PyTorch深度学习实战(12)——数据增强
PyTorch深度学习实战(12)——数据增强 0. 前言1. 图像增强1.1 仿射变换1.2 亮度修改1.3 添加噪音1.4 联合使用多个增强方法 2. 对批图像执行图像增强3. 利用数据增强训练模型小结系列链接 0. 前言 数据增强是指通过对原始数据进行一系列变换和处理&…...
SpringCloud Ribbon中的7种负载均衡策略
SpringCloud Ribbon中的7种负载均衡策略 Ribbon 介绍负载均衡设置7种负载均衡策略1.轮询策略2.权重策略3.随机策略4.最小连接数策略5.重试策略6.可用性敏感策略7.区域敏感策略 总结 负载均衡通器常有两种实现手段,一种是服务端负载均衡器,另一种是客户端…...
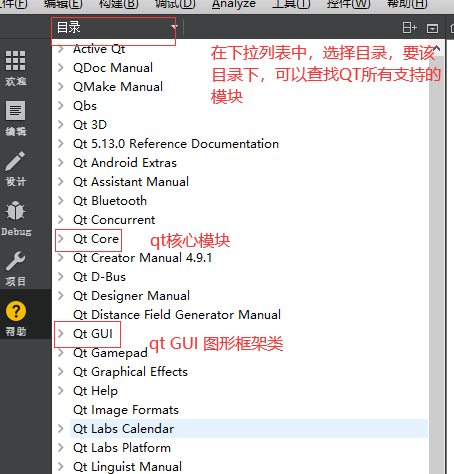
04 qt功能类、对话框类和文件操作
一 QT中时间和日期 时间 ---- QTime日期 ---- QDate对于Qt而言,在实际的开发过程中, 1)开发者可能知道所要使用的类 ---- >帮助手册 —>索引 -->直接输入类名进行查找 2)开发者可能不知道所要使用的类,只知道开发需求文档 ----> 帮助 手册,按下图操作: 1 …...
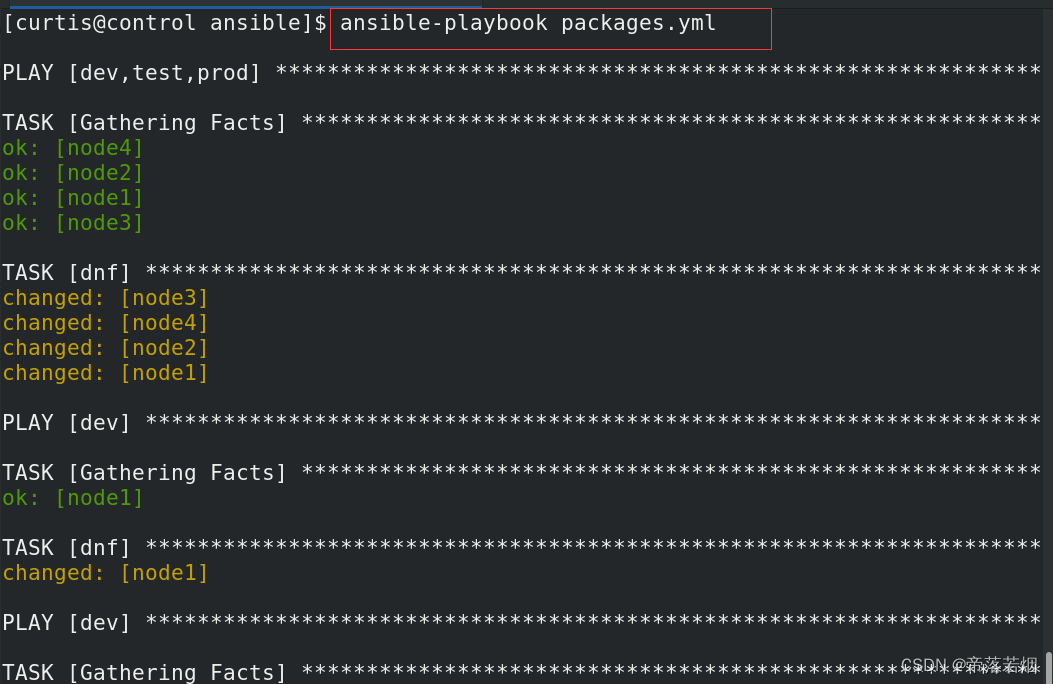
安装软件包
安装软件包 创建一个名为 /home/curtis/ansible/packages.yml 的 playbook : 将 php 和 mariadb 软件包安装到 dev、test 和 prod 主机组中的主机上 将 RPM Development Tools 软件包组安装到 dev 主机组中的主机上 将 dev 主机组中主机上的所有软件包更新为最新版本 vim packa…...

玩转单元测试之gmock
引言 前文我们学习了gtest相关的使用,单靠gtest,有些场景仍然无法进行测试,因此就诞生了gmock。 gmock快速入门 在引入gtest时,gmock也同样引入了,因此只需要在编译时加上合适的编译选项即可,注意不同版…...

POI与EasyExcel--写Excel
简单写入 03和07版的简单写入注意事项: 1. 对象不同:03对应HSSFWorkbook,07对应XSSFWorkbook 2. 文件后缀不同:03对应xls,07对应xlsx package com.zrf;import org.apache.poi.hssf.usermodel.HSSFWorkbook; import …...
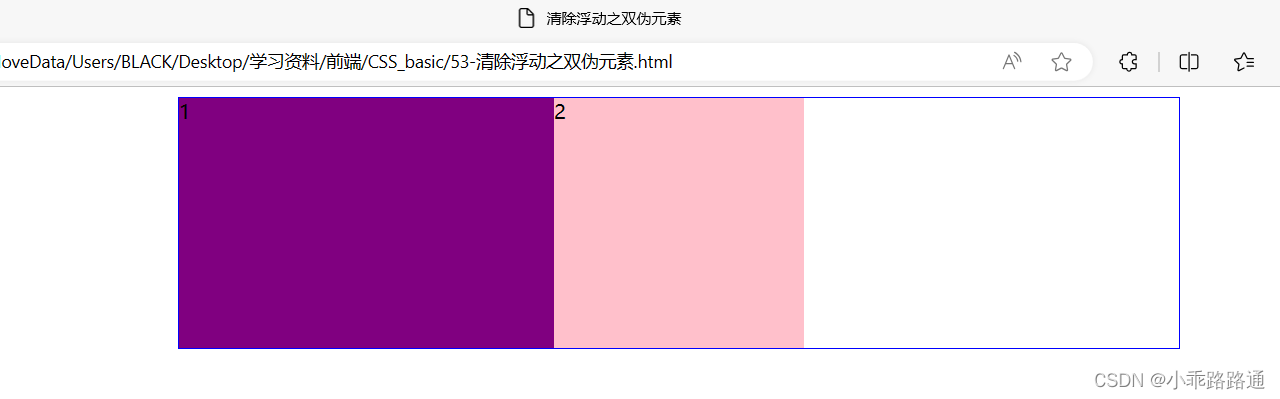
7. CSS(四)
目录 一、浮动 (一)传统网页布局的三种方式 (二)标准流(普通流/文档流) (三)为什么需要浮动? (四)什么是浮动 (五)浮…...

uni-app 集成推送
研究了几天,终于是打通了uni-app的推送,本文主要针对的是App端的推送开发过程,分为在线推送和离线推送。我们使用uni-app官方推荐的uni-push2.0。官方文档 准备工作:开通uni-push功能 勾选uniPush2.0点击"配置"填写表单…...

Spring Boot+Redis 实现消息队列实践示例
Spring BootRedis 实现一个轻量级的消息队列 文章目录 Spring BootRedis 实现一个轻量级的消息队列0.前言1.基础介绍2.步骤2.1. 引入依赖2.2. 配置文件2.3. 核心源码 4.总结答疑 5.参考文档6. Redis从入门到精通系列文章 0.前言 本文将介绍如何利用Spring Boot与Redis结合实现…...
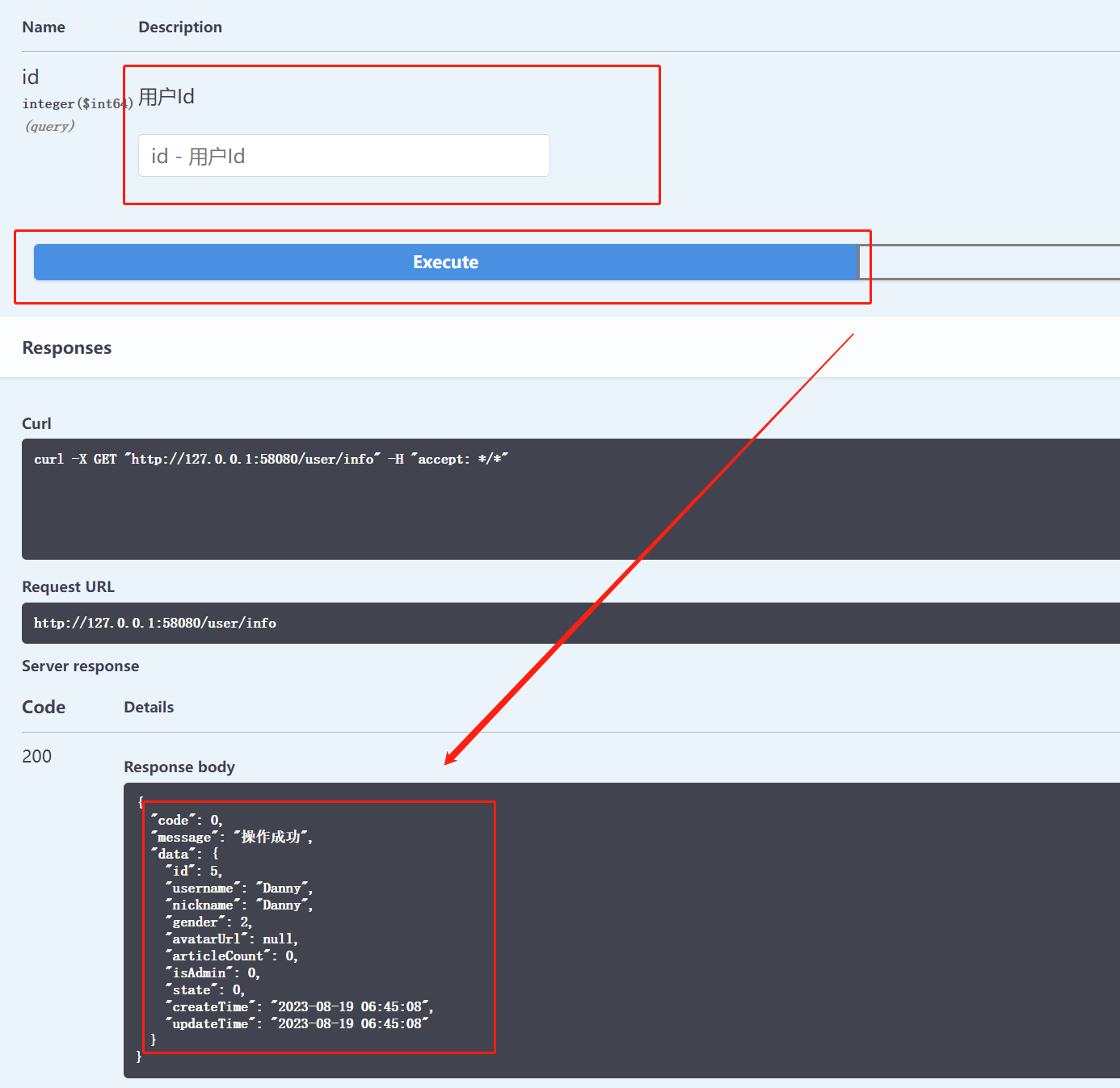
11. 实现业务功能--获取用户信息
目录 1. 实现 Controller 2. 单体测试 3. 修复返回值存在的缺陷 3.1 用户的隐私数据:密码的密文和盐不能显示 3.2 将值为 null 的字段可以进行过滤 3.3 时间的格式需要进行处理,如 yyyy-mmmm-ddd HH:mm:ss 3.4 data 属性没有返回 4. 实现前端页…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

【无标题】湖北理元理律师事务所:债务优化中的生活保障与法律平衡之道
文/法律实务观察组 在债务重组领域,专业机构的核心价值不仅在于减轻债务数字,更在于帮助债务人在履行义务的同时维持基本生活尊严。湖北理元理律师事务所的服务实践表明,合法债务优化需同步实现三重平衡: 法律刚性(债…...

AD学习(3)
1 PCB封装元素组成及简单的PCB封装创建 封装的组成部分: (1)PCB焊盘:表层的铜 ,top层的铜 (2)管脚序号:用来关联原理图中的管脚的序号,原理图的序号需要和PCB封装一一…...
