秒懂算法│博弈论

博弈论是二人或多人在平等的对局中各自利用对方的策略变换自己的对抗策略,达到取胜目标的理论。博弈论是研究互动决策的理论。博弈可以分析自己与对手的利弊关系,从而确立自己在博弈中的优势,因此有不少博弈理论,可以帮助对弈者分析局势,从而采取相应策略,最终达到取胜的目的。
01、最小最大问题
最小最大问题( minimax ):用于确定计算机玩家在诸如井字游戏、跳棋、奥赛罗和国际象棋中的哪一步。这类游戏被称为完美信息游戏,因为它可以看到所有可能的动作。拼字游戏并不是一个完美信息的游戏,因为你看不到对手的手,所以无法预测对手的动作。
可以把这个算法想象成人类的思维过程:如果我做这个动作,那么我的对手只能做两个动作,每个动作都会让我赢。所以这是正确的选择。
用博弈树数据结构表示井字游戏如图 1 所示。
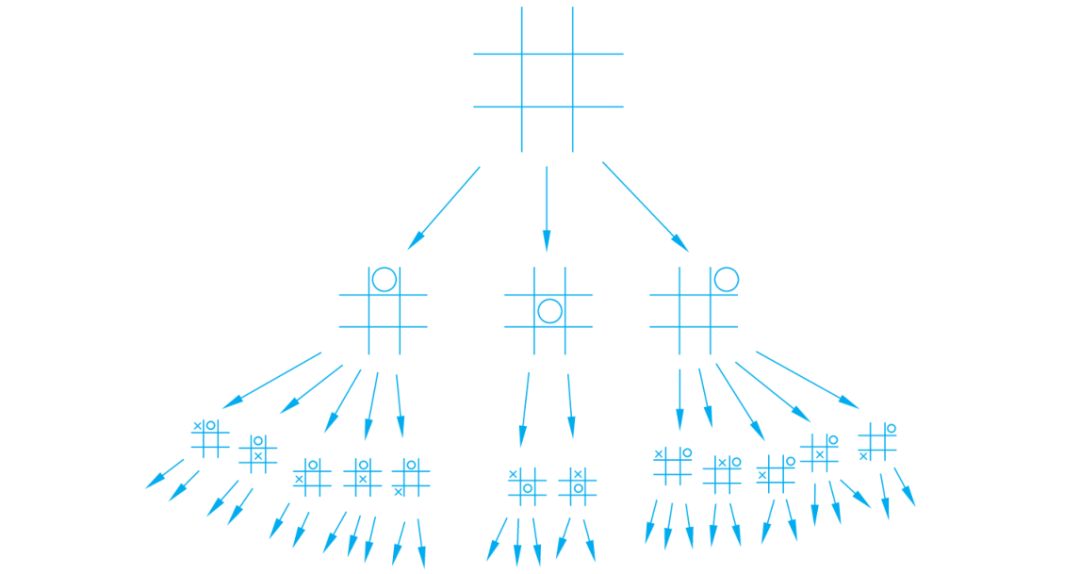
■ 图1 用博弈树数据结构表示井字游戏
如果你认为所谓最小最大就是穷举过程中找到的最差走法和最佳走法那就错了,既然是对立的概念,当然是两个对象,这里的最小最大是当前轮到 AI 走了, AI 进行穷举并选择一条对于 AI 来说最佳而对于人来说最差的走法,但是再考虑一下,机器也是有限的,对于象棋这样棋盘较大的游戏,穷举完博弈树在当前科技下不可能,因此我们的最小最大算法需要一个深度,即向前走几步,计算机就能在这个指定的比较小的整数下完成对博弈树的穷举。
当遍历若干树枝后不可能就结束了,如果在游戏没有结束的情况下我们还需要一个评价启发函数,这个函数用于判断当前策略的价值,如果使用某走法能赢,就返回一个大的正数;如果这种走法会输,就返回一个大的负值;如果走法会产生和局,就返回一个 0 左右的数;如果由于当前博弈树深度没办法判断局面,那么评价函数就会返回一个启发值。
参考程序:
#include<cstdio>
int MaxMin(int depth,int player mode)
{
int best = INFINITY(player mode);
//player mode 是参照物,如果当前落子是人,则返回一个很小的值,反之返回一个很大的值
if (depth <= 0) //当前以局面为博弈树的根
return Evaluate() ; //估值函数
}
GenerateLegalMoves () ;//生成当前所有走法
while (MovesLeft () ) //遍历每一个走法
{
MakeNextMove () ;//实施走法
val = -MaxMin(depth - 1);//换位思考
UnmakeMove() ;//撤销走法
if (val > best)
best = val;
return best;
} 02、巴什博弈
A和B一块报数,每人每次最少报1个,最多报4个,看谁先报到30。这应该是最古老的关于巴什博弈(Bash game)的游戏了。
其实如果知道原理,这个游戏一点运气成分都没有,只和先手、后手有关,比如第一次报数,A报k个数,那么B报5-k个数,那么B报数之后问题就变为,A和B一起报数,看谁先报到25了,进而变为20,15,10,5,当到5的时候,不管A怎么报数,最后一个数肯定是B报的,可以看出,作为后手的B在个游戏中是不会输的。
那么如果要报n个数,每次最少报1个,最多报m个,我们可以找到这么一个整数k和r,使n=k*(m+1)+r,代入上面的例子可以知道,如果r=0,那么先手必败;否则先手必胜。
巴什博弈: 有n个物品,两个人轮流从中取物,规定每次最少取1个,最多取m个,最后取光者为胜。
参考程序:
#include <iostream>
using namespace std;
int main()
int n,m;
while(cin>>n>>m)
cout<<"后手必胜“< <endl;if(n%(m+1)==0)else cout<<"先手必胜"< <endl;
return 0;例题如下。
题目大意: 小唐和小红轮流写数字,小唐先写,每次写的数x满足1≤x≤k,小红每次写的数y满足1≤y-x≤k,谁先写到不小于n的数算输。
结论: r=(n-1)%(k+1),r=0时小红胜,否则小唐胜。
详解:
巴什博弈: 同余理论。
从n个物品中两人轮流取,每次取1~m个,最后取完者为胜。
比如10个物品,每次只能取1~5个,则先手方必赢。
(1) 面对[1…m]个局面,必胜。
(2) 面对m+1个局面,必输。
(3) 如果可以使对手面临必输局面,那么是必赢局面。
(4) 如果不能使对手面临必输局面,那么是必输局面。
基础: 1, 2,…, m是必赢局面,m+1是必输局面。
递推: m+2,m+3,…,2m+1是必赢局面,2m+2是必输局面。
k(m+1)是必输局面,应该允许k=0,因为0显然也是必输局面。
在必输局和必赢局中,赢的一方的策略是: 拿掉部分物品,使对方面临k(m+1)的局面。
例如,上例中10个物品,只能拿1~5个,先手方拿4个即可,对手无论拿多少个,你下次总能拿完。
从另一个角度思考这个问题,如果物品数量随机,那么先手方胜利的概率是m/(m+1),后手方胜利的概率是1/(m+1)。
03、斐波那契博弈
两人轮流从一堆物品中取物品,先手最少取一个,至多无上限,但不能把物品取完,之后每次取的物品数不能超过上次取的物品数的二倍且至少为一件,取走最后一件物品的人获胜。
结论:先手胜当且仅当 n 不是斐波那契数(n 为物品总数)。
# include <iostream>
# include <string.h>
# include <stdio.h>
using namespace std;
const int N = 55;
int f[N];
void Init()
{
f[O] = f[1] = 1;
for(int i=2;i<N;i++)
f[i] = f[i-1] + f[i-2];
}
int main()
{
Init();
int n;
while(cin>>n)
if(n == 0) break;
bool flag = 0;
for(int i=0;i<N;i++)
{
if(f[i] == n)
{
flag = 1;
break;
}
if(flag) puts("Second win") ;
else
puts("First win");
R
}
return 0;
}相关文章:

秒懂算法│博弈论
博弈论是二人或多人在平等的对局中各自利用对方的策略变换自己的对抗策略,达到取胜目标的理论。博弈论是研究互动决策的理论。博弈可以分析自己与对手的利弊关系,从而确立自己在博弈中的优势,因此有不少博弈理论,可以帮助对弈者分析局势,从而采取相应策略,最终达到取胜的目的。…...

Springboot整合RabbitMQ消息中间件
spring-boot-rabbitmq–消息中间件整合 前言:RabbitMQ的各种交换机说明 1、直连交换机 生产者发布消息时必须带着routing-key,队列绑定到交换机时必须指定binding-key ,且routing-key和binding-key必须完全相同,如此才能将消息路由到队列中…...
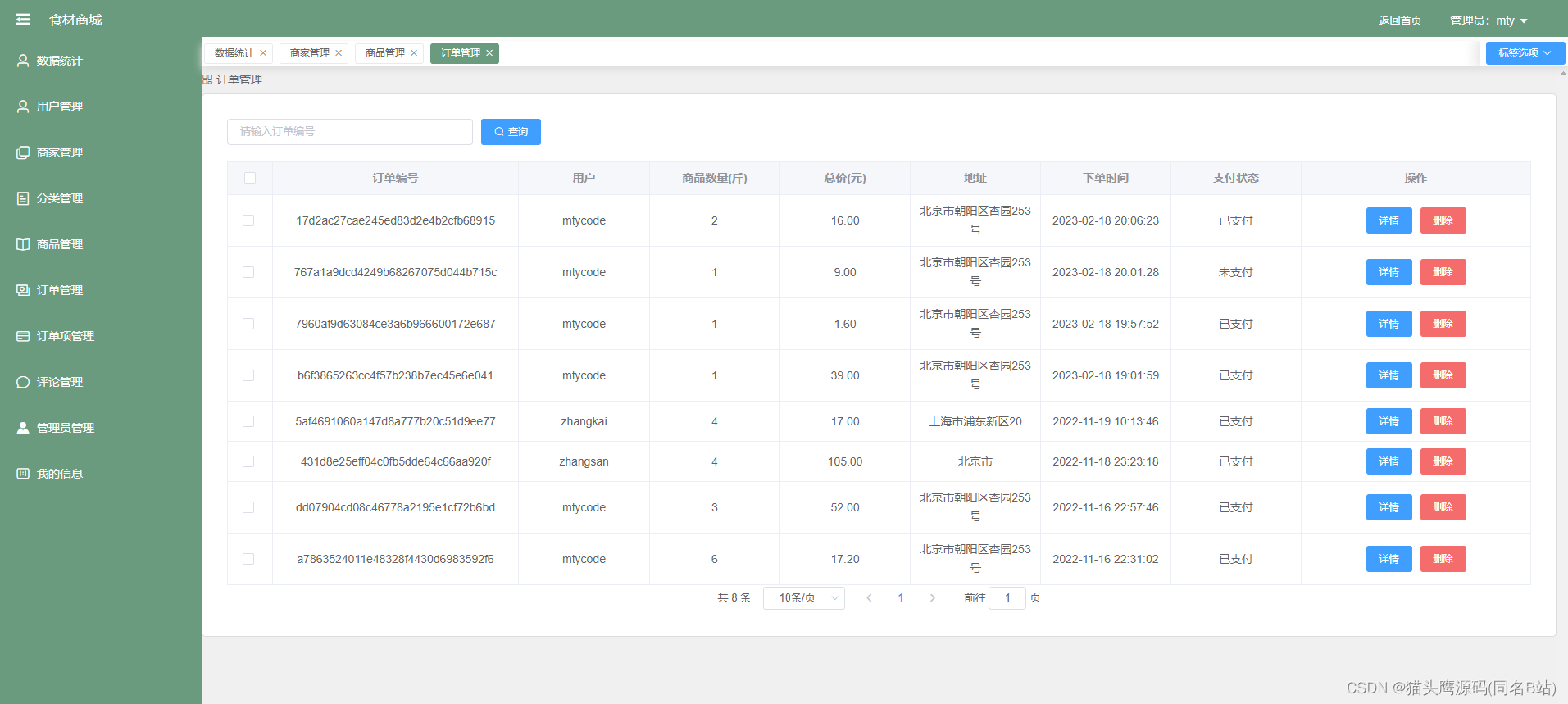
基于springboot+vue的食材商城(前后端分离)
博主主页:猫头鹰源码 博主简介:Java领域优质创作者、CSDN博客专家、公司架构师、全网粉丝5万、专注Java技术领域和毕业设计项目实战 主要内容:毕业设计(Javaweb项目|小程序等)、简历模板、学习资料、面试题库、技术咨询 文末联系获取 项目介绍…...
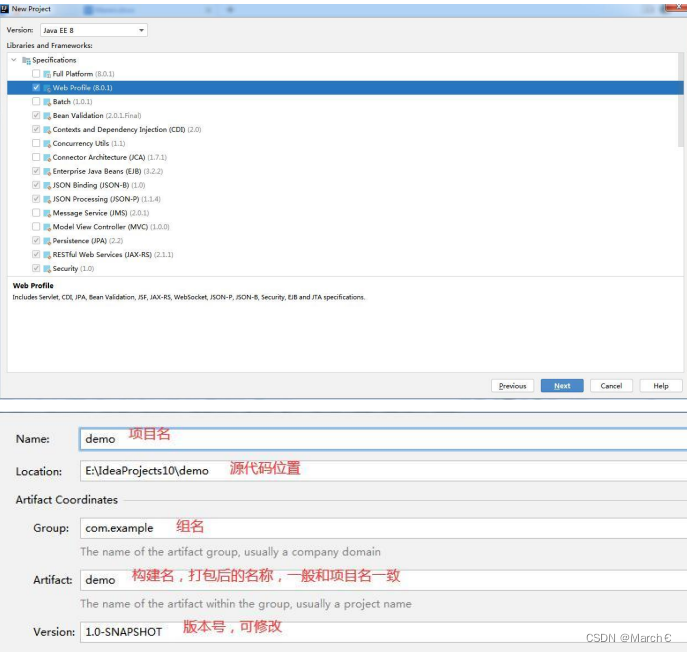
Maven解析
目录 Maven的概念 Pom 项目坐标 仓库 Maven环境搭建 安装jdk 配置maven 配置本地仓库地址 配置阿里云 maven 镜像仓库,下载速度更快 在idea中配置maven 编辑 pom中名词解释 Maven命令 Maven的概念 Maven 是 Apache 软件基金会的一个开源项目,是一个…...

如何使用数学将 NumPy 函数的性能提高 50%
一、说明 2D 傅里叶变换是本世纪最重要的计算机科学算法之一。它已在我们的日常生活中得到应用,从Instagram过滤器到MP3文件的处理。 普通用户最常用的实现,有时甚至是在不知不觉中,是 NumPy 的改编。然而,尽管它很受欢迎…...
| 社情民意调查的内容)
群狼调研(长沙政策第三方评估)| 社情民意调查的内容
本文由群狼调研(长沙社会舆情调查)出品,欢迎转载,请注明出处。社情民意调查旨在捕捉公众对各种社会问题的态度、意见和看法,社情民意调查的内容通常包括以下几个方面: 1. 社会热点问题:针对当前社会热点问题进行调查&…...
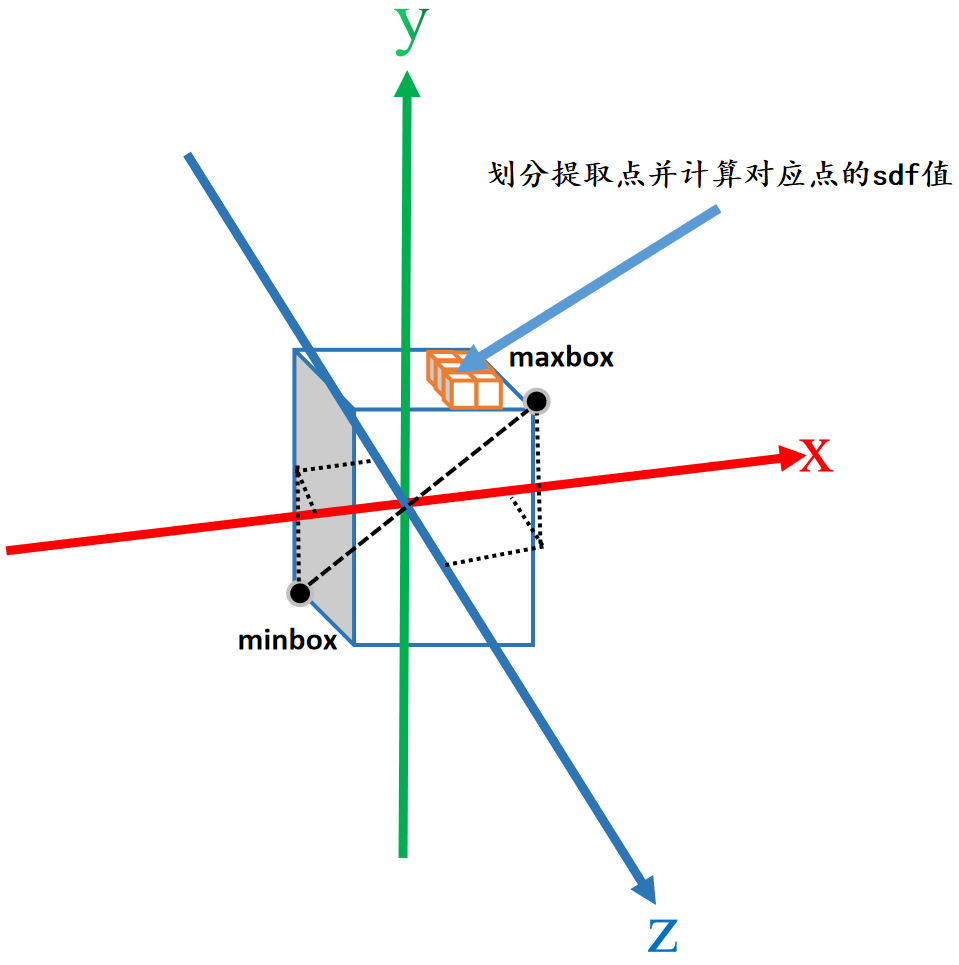
【三维重建】【深度学习】NeuS代码Pytorch实现--测试阶段代码解析(上)
【三维重建】【深度学习】NeuS代码Pytorch实现–测试阶段代码解析(上) 论文提出了一种新颖的神经表面重建方法,称为NeuS,用于从2D图像输入以高保真度重建对象和场景。在NeuS中建议将曲面表示为有符号距离函数(SDF)的零级集,并开发一种新的体绘…...
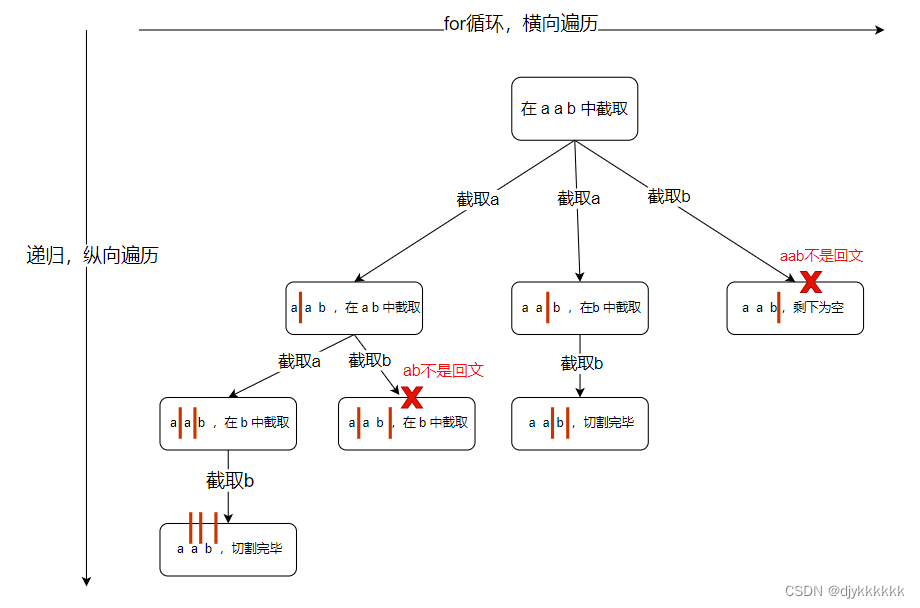
day-24 代码随想录算法训练营(19)回溯part01
77.组合 思路一:回溯相当于枚举,所以我们遍历1-n的每一个数字,然后在遍历第i位的同时递归出第i1~n位的组合结果,跟树的形式相似。 如上图所示,当长度为k时,即退出递归可对遍历到第i位以及剩下位数与k进行比…...

Redis之SYNC与PSYNC命令
一、复制SYNC与PSYNC 在Redis主从架构中,主要有以下两种情形需要进行数据同步 (1)当新的服务器执行slave of 命令,成为主服务器的从服务器。这时候从服务器会向主服务器发送SYNC命令,请求全量同步数据,主服…...

共创无线物联网数字化新模式|协创数据×企企通采购与供应链管理平台项目成功上线
近日,全球无线物联网领先者『协创数据技术股份有限公司』(以下简称“协创数据”)SRM采购与供应链项目全面上线,并于近日与企企通召开成功召开项目上线总结会。 基于双方资源和优势,共同打造了物联网特色的数字化采购供…...

【深入理解jvm读书笔记】jvm如何进行内存分配
jvm如何进行内存分配 内存分配方式内存分配方式的选择并发场景下的内存分配内存空间的初始化构造函数 内存分配方式 指针碰撞空闲列表 指针碰撞法: 假设Java堆中内存是绝对规整的,所有被使用过的内存都被放在一边,空闲的内存被放在另一边&a…...
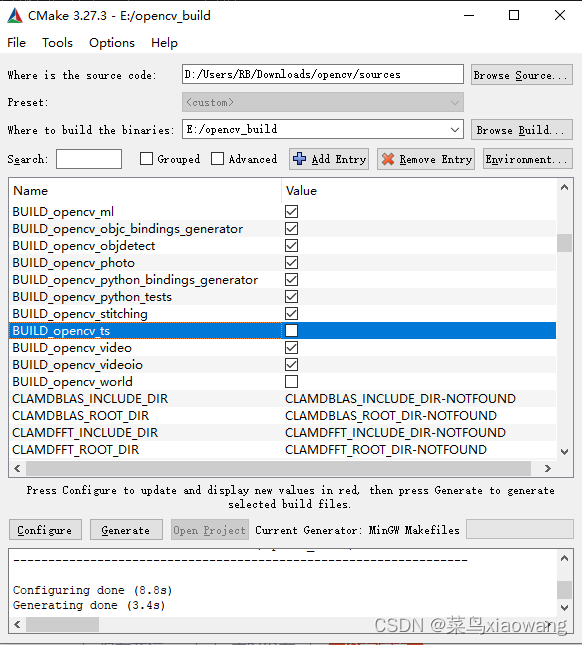
OpenCV使用CMake和MinGW-w64的编译安装
OpenCV使用CMake和MinGW-w64的编译安装中的问题 问题:gcc: error: long: No such file or directory** C:\PROGRA~2\Dev-Cpp\MinGW64\bin\windres.exe: preprocessing failed. modules\core\CMakeFiles\opencv_core.dir\build.make:1420: recipe for target ‘modul…...
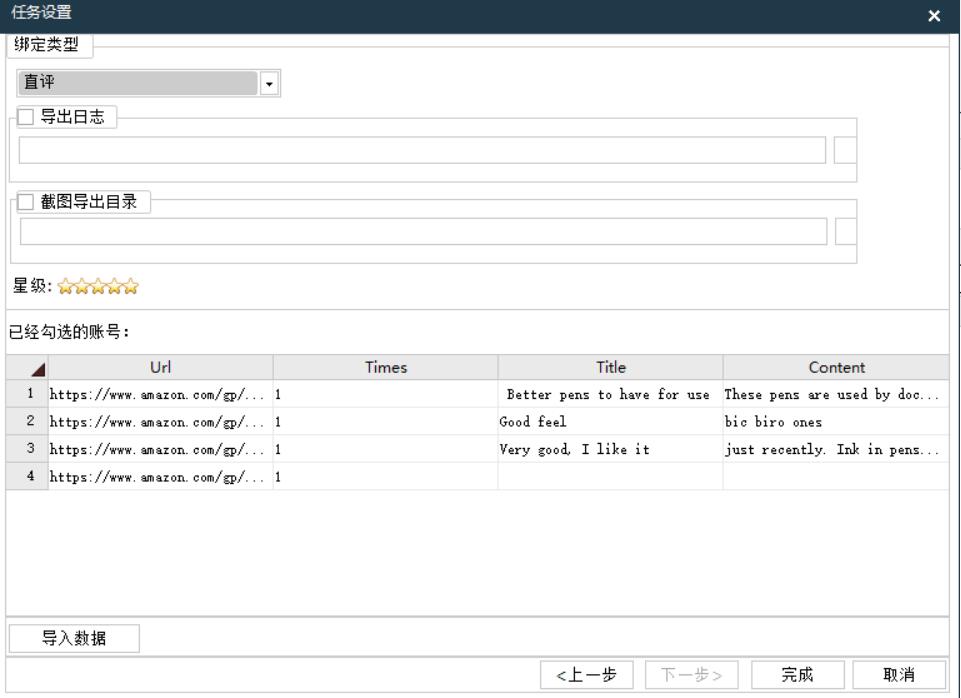
亚马逊买家怎么留评
亚马逊买家可以按照以下步骤在购买后留下产品评价: 1、登录亚马逊账户:首先,在网页浏览器中打开亚马逊网站,登录你的亚马逊账户。 2、找到订单:在页面上找到并点击你购买过的商品的"我的订单"或"订单…...
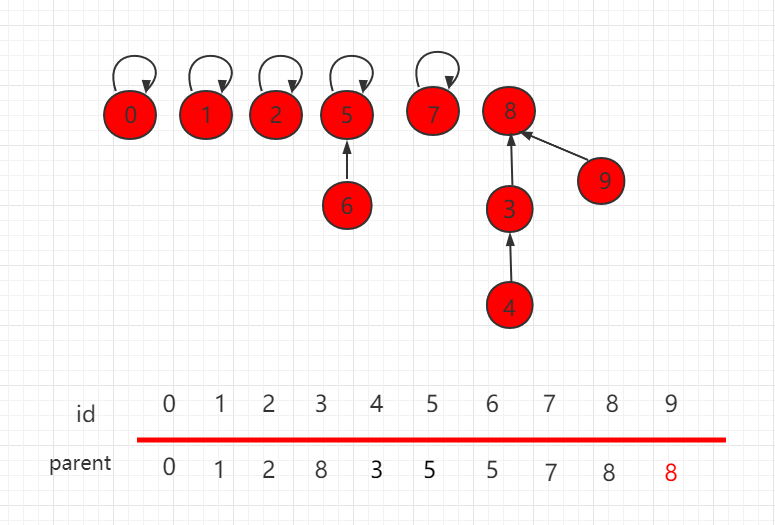
并查集 size 的优化(并查集 size 的优化)
目录 并查集 size 的优化 Java 实例代码 UnionFind3.java 文件代码: 并查集 size 的优化 按照上一小节的思路,我们把如下图所示的并查集,进行 union(4,9) 操作。 合并操作后的结构为: 可以发现,这个结构的树的层相对…...
Qt关于hex转double,或者QByteArray转double
正常的00 ae 02 33这种类型的hex数据类型可以直接通过以下代码进行转换 double QDataConversion::hexToDouble(QByteArray p_buf) {double retValue 0;if(p_buf.size()>4){QString str1 byteArrayToHexStr(p_buf.mid(0,1));QString str2 byteArrayToHexStr(p_buf.mid(1,…...
Java“牵手”根据关键词搜索(分类搜索)拼多多商品列表页面数据获取方法,拼多多API实现批量商品数据抓取示例
拼多多商城是一个网上购物平台,售卖各类商品,包括服装、鞋类、家居用品、美妆产品、电子产品等。要获取拼多多商品列表和商品详情页面数据,您可以通过开放平台的接口或者直接访问拼多多商城的网页来获取商品列表和详情信息。以下是两种常用方…...

Linux相关知识点
Linux是什么? Linux是一套免费使用和自由传播的类Unix操作系统,是一个基于POSIX和UNIX的多用户、多任务、支持多线程和多CPU的操作系统。它能运行主要的UNIX工具软件、应用程序和网络协议。它支持32位和64位硬件。 Linux内核 是一个Linux系统的内核&…...

常见的的数据结构
数组(Array):一组按顺序排列的元素的集合,可以通过索引访问和修改元素。 链表(Linked List):由一系列节点组成的数据结构,每个节点包含数据和指向下一个节点的指针。 栈࿰…...

专业心理咨询师助你轻装上阵,向内耗说不!
引言 身为技术人,你是否经常感觉自己被掏空了精力,行动力不佳?又或者觉得自己的工作没有成就和意义,工作状态持续不佳?你是否总有一种无法消除的疲惫?即使没有学习、工作,而是选择看剧、刷短视频…...

Ubuntu安装mysql5.7
目录 1. 更新系统软件包2. 安装MySQL 5.73. 启动MySQL 服务4. 设置MySQL root 密码5. 验证MySQL 安装6. 启用远程访问7. 创建新用户8. 为新用户授予权限9. mysql命令 以Ubuntu 18.04系统为例,安装MySQL 5.7。操作步骤如下: 1. 更新系统软件包 sudo apt…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...
